A weighted-sum chaotic sparrow search algorithm for interdisciplinary feature selection and data classification

Abstract

In today’s data-driven digital culture, there is a critical demand for optimized solutions that essentially reduce operating expenses while attempting to increase productivity. The amount of memory and processing time that can be used to process enormous volumes of data are subject to a number of limitations. This would undoubtedly be more of a problem if a dataset contained redundant and uninteresting information. For instance, many datasets contain a number of non-informative features that primarily deceive a given classification algorithm. In order to tackle this, researchers have been developing a variety of feature selection (FS) techniques that aim to eliminate unnecessary information from the raw datasets before putting them in front of a machine learning (ML) algorithm. Meta-heuristic optimization algorithms are often a solid choice to solve NP-hard problems like FS. In this study, we present a wrapper FS technique based on the sparrow search algorithm (SSA), a type of meta-heuristic. SSA is a swarm intelligence (SI) method that stands out because of its quick convergence and improved stability. SSA does have some drawbacks, like lower swarm diversity and weak exploration ability in late iterations, like the majority of SI algorithms. So, using ten chaotic maps, we try to ameliorate SSA in three ways: (i) the initial swarm generation; (ii) the substitution of two random variables in SSA; and (iii) clamping the sparrows crossing the search range. As a result, we get CSSA, a chaotic form of SSA. Extensive comparisons show CSSA to be superior in terms of swarm diversity and convergence speed in solving various representative functions from the Institute of Electrical and Electronics Engineers (IEEE) Congress on Evolutionary Computation (CEC) benchmark set. Furthermore, experimental analysis of CSSA on eighteen interdisciplinary, multi-scale ML datasets from the University of California Irvine (UCI) data repository, as well as three high-dimensional microarray datasets, demonstrates that CSSA outperforms twelve state-of-the-art algorithms in a classification task based on FS discipline. Finally, a 5%-significance-level statistical post-hoc analysis based on Wilcoxon’s signed-rank test, Friedman’s rank test, and Nemenyi’s test confirms CSSA’s significance in terms of overall fitness, classification accuracy, selected feature size, computational time, convergence trace, and stability.

Introduction

The twenty-first century has become the era of data, with data analysis and utilization visible everywhere in all aspects of life, and these data are frequently of high-dimensional character^1,2,3,4,5. However, it is inevitable that this data will contain a substantial number of redundant and irrelevant characteristics, increasing the computational overhead and risk of overfitting when handled by traditional machine learning (ML) algorithms^6,7,8. As a result, in order to make better use of the data, efficient procedures, such as feature selection (FS), must be developed to handle the worthless features^9,10,11. Wrappers, filters, and embedded FS techniques are commonly used to differentiate them based on their evaluation for feature subsets¹². Wrapper-based approaches rely on predefined ML algorithms to obtain higher classification accuracy but are very expensive to compute because the ML algorithms must be run numerous times¹³. On the contrary, while evaluating feature subsets, filter-based approaches do not use any ML algorithms, which reduces computing cost but may reduce classification accuracy¹⁴. Embedded techniques incorporate FS into model learning, accounting for the influence of the algorithmic model while lowering computational weight; however, these methods have poor generalization ability and significant computational complexity¹⁵.

Because the number of feature subsets varies geometrically due to data dimensionality, it is challenging to produce adequate results using traditional methods, especially when working on high-dimensional data. To reduce the high computational cost caused by the curse of dimensionality, novel feature subset selection approaches can be developed based on wrapper swarm intelligence (SI) algorithms due to their robustness and adjustability^16,17,18. SI algorithms have three essential characteristics: flexibility, self-organization, and resilience. These algorithms are often inspired by group behavior in nature, such as foraging, anti-predation, and migration¹⁹. Typical SI algorithms are ant colony optimization (ACO)²⁰, particle swarm optimization (PSO)²¹, grey wolf optimizer (GWO)²², artificial bee colony (ABC)²³, whale optimization algorithm (WOA)²⁴, grasshopper optimization algorithm (GOA)²⁵, harris hawks optimization (HHO)²⁶, and bird swarm algorithm (BSA)²⁷. Other optimization algorithms include bat algorithm (BA)²⁸, atom search optimization (ASO)²⁹, and henry gas solubility optimization (HGSO)³⁰. In general, meta-heuristic algorithms can effectively handle FS problems, lowering computational complexity while achieving a greater classification accuracy, and SI approaches have, therefore, been consistently applied to FS problems^31,32,33,34. For instance, Hussain et al.³⁵ integrated the sine-cosine algorithm (SCA) into HHO to balance the exploration and exploitation capabilities of HHO, and experimental results on several numerical optimization as well as FS problems revealed the competitive advantage of the proposed algorithm over other SI algorithms. Neggaz et al.³⁶ first applied HGSO to solving FS problems. Experimental results on datasets with different feature sizes (from 13 to 15009) showed that HGSO is effective in minimizing feature size, especially on high-dimensional data, while preserving maximum classification accuracy.

Nevertheless, SI algorithms tend to fall into local optimization due to: (i) the imbalance between exploration and exploitation; and (ii) super stochasticity^37,38. Numerous studies have shown that chaos theory can defeat such an issue owing to its characteristics of semi-stochastic, ergodicity, and sensitivity to the initial swarm^39,40. Khosravi et al.⁴¹ incorporated a new local search strategy and the Piecewise chaotic map, in order to make their teaching optimization algorithm capable of tackling high-dimensional FS problems. Zhang et al.⁴² integrated the Gaussian’s mutation and the Logistic chaotic map into the fruit fly algorithm (FFA) to avoid premature convergence and hence strengthen the exploration capability. Sayed et al.⁴³ optimized the crow search algorithm (CSA) by using ten chaotic maps to improve its performance in tackling FS problems in terms of classification accuracy, number of selected features, and convergence speed. Altay et al.⁴⁴ replaced the random parameters in BSA with ten chaotic maps to boost the exploration ability.

The sparrow search algorithm (SSA) is one of many recently developed SI algorithms. In it, the sparrow is a dexterous species that forages through collective collaboration and can effectively escape natural predators. SSA was proposed by Xue et al.⁴⁵ by emulating such properties. When compared to its counterparts, SSA has garnered a lot of attention because of its fast convergence, great search efficiency, and stability^{46,47,48,49,50,51}. However, SSA suffers from the same flaws as other SI algorithms in that swarm diversity and exploratory abilities decrease as the algorithm progresses^47,52. As a result, significant enhancements have been made to SSA. To make SSA more thorough in exploring the solution space, Xue et al.⁵³ utilized a new neighbor search approach. Gao et al.⁵² added a chaotic map and a mutation evolution technique to SSA to improve its robustness and convergence speed. Gad et al.⁵⁴ binarized SSA using S- and V-shaped functions and included a random relocation approach for transgressive sparrows as well as a new local search strategy to balance its exploration and exploitation capabilities. Lyu et al.⁵⁵ used the Tent chaotic map and the Gaussian mutation technique to improve SSA and apply it to simple image segmentation challenges. Furthermore, Yang et al.⁵⁶ improved SSA with the use of the Sine chaotic map, an adaptive weighting approach, and an adaptive t-distribution mutation operator, and then applied the suggested technique to numerical optimization problems. However, no one has yet used a chaos-improved SSA to solve FS problems. SI algorithm performance can generally be improved in three ways: (i) adjusting their parameters; (ii) altering their mechanisms; and (iii) combining them with other algorithms⁵⁷. In light of this, this work aims to improve SSA by redefining its random parameters and procedures through the use of a chaotic map. The following are the main contributions:

• 1. The initial swarm, transgressive positions, and random variables in SSA are processed by using chaotic maps to simultaneously boost its swarm diversity and make a good trade-off between exploration and exploitation in it. Comparing twenty different chaos-improved SSA variants yields the best chaotic SSA (CSSA).

• 2. CSSA is compared against twelve peer algorithms, including SSA, ABC, PSO, BA, WOA, GOA, HHO, BSA, ASO, HGSO, success-history based adaptive differential evolution with linear population size reduction (LSHADE)⁵⁸ and evolution strategy with covariance matrix adaptation (CMAES)⁵⁹, on some representative functions from the Institute of Electrical and Electronics Engineers (IEEE) Congress on Evolutionary Computation (CEC) and eighteen multi-scale datasets from the University of California Irvine (UCI) data repository as a scaffold to verify its competitiveness. Furthermore, this study also selects seven recently proposed FS methods from the literature to verify that CSSA still has advantages over several state-of-the-art algorithms.

• 3. The capability of CSSA is further tested on three high-dimensional microarray datasets with a number of features/genes (dimensions) up to 12500.

• 4. We empirically and theoretically measure the strengths and weaknesses of CSSA against different algorithms to solve FS problems under evaluation metrics, such as overall fitness, classification accuracy, selected feature size, convergence, and stability.

• 5. A post-hoc statistical analysis, including Wilcoxon’s signed-rank test, Friedman’s rank test, and Nemenyi’s test, is conducted at a 5% significance level to verify the statistical significance of CSSA over its peers.

Following that, this article is organized as follows. Section Preliminaries introduces the SSA principle and the ten chaotic maps that have been tested with it, whereas Sect. Proposed chaotic sparrow search algorithm (CSSA) presents the proposed CSSA. Section Experimental results and discussion compares CSSA to twelve peer algorithms and seven popular FS approaches in the literature, and experimental data on eighteen UCI datasets and three high-dimensional microarray datasets are provided and analyzed. Section Discussion discusses CSSA’s strengths and limitations. Finally, Sect. Conclusion concludes the paper.

Preliminaries

Sparrow search algorithm (SSA)

This section presents a brief history of SSA and its mathematical formulation. SSA is a recently developed SI algorithm that in a mathematical language mimics the foraging and anti-predatory behaviors of sparrows. In general, sparrows are classed as producers or scroungers based on their fitness values, which are assessed on a regular basis using individuals’ current positions. Producers are largely responsible for supplying food to the swarm, whereas scroungers often use producers as a means to get a source of food. In addition, as predators approach the swarm, some scouters modify their positions to protect themselves and the entire swarm. As a result, the sparrow swarm can continuously gather food while also ensuring security for the swarm’s reproduction under various strategies. Different species of sparrows have different roles, and the following are the components of SSA and its algorithmic process.

Step 1:

The swarm is initialized. SSA first randomly generates the initial positions of a group of sparrows as

$$\begin{aligned} {\textbf{X}}=\left[ \begin{array}{c} {\textbf{x}}_{1} \\ {\textbf{x}}_{2}\\ \vdots \\ {\textbf{x}}_{N} \end{array}\right] = \left[ \begin{array}{cccc}x_{1,1} &{} x_{1,2} &{} \ldots &{} x_{1, D} \\ x_{2,1} &{} x_{2,2} &{} \ldots &{} x_{2, D} \\ \vdots &{} \vdots &{} \ldots &{} \vdots \\ x_{N, 1} &{} x_{N, 2} &{} \ldots &{} x_{N, D}\end{array}\right] \text {, } x_{i,j} \sim U{(0,1)}, \end{aligned}$$

(1)

where N denotes the number of individuals in the swarm, D represents the dimensionality of a decision vector (or the number of features in a dataset being processed in the case of FS problems), and $x_{i,j}$ denotes a value taken by a sparrow i in a dimension j. SSA judges the quality of obtained solutions via a fitness function

$$\begin{aligned} \mathbf {F({\textbf{X}})}=\left[ \begin{array}{c}f({\textbf{x}}_{1}) \\ f({\textbf{x}}_{2}) \\ \vdots \\ f({\textbf{x}}_{N}) \end{array}\right] , \end{aligned}$$

(2)

where a fitness function f(.) is used to evaluate the quality of a given solution ${\textbf{x}}_i$.

Step 2:

The producer is mainly responsible for finding food sources, and its position update rules are

$$\begin{aligned} {\textbf{x}}_i^{t+1}=\left\{ \begin{array}{lll}{\textbf{x}}_i^{t} \exp \left( \frac{-i}{\alpha T}\right) , &{} \text{ if } &{} R_{2}<ST\\ {\textbf{x}}_i^{t}+QL, &{} \text{ if } &{} R_{2} \ge ST\end{array}\right. \end{aligned}.$$

(3)

SSA improves the quality of its solutions by exchanging information among its consecutive iterations. Eq. (3) is used to describe the way information is exchanged between producers as the number of iterations increases. t denotes current iteration’s number. Since SSA is not used to find the global optimal solution, but to provide a relatively better solution, the maximum number of iterations T is usually used as the condition for the termination of the algorithm. $\alpha$ usually has a random value in the range [0, 1]. The warning value $R_2 \sim U{(0,1)}$ indicates the hazard level of a producer’s location, while the safety value $ST \in [0.5,1]$ is a threshold value used to determine whether a producer’s location is safe. $R_2<ST$ indicates that the producer is in a safe environment and can search extensively; otherwise, the producer is at risky location of predation and needs to fly away. Q is a random parameter that follows a normal distribution. L denotes a $1 \times D$ matrix with all its elements having values equal to 1.

Step 3:

The swarm in SSA can be divided into producers and scroungers. The scroungers renew themselves as

$$\begin{aligned} {\textbf{x}}_i^{t+1}=\left\{ \begin{array}{lll}Q \exp \left( \frac{{\mathbf{g}}_{worst}^{t}-{\textbf{x}}_i^{t}}{i^2}\right) , &{} \text { if } i>N / 2 \\ {\mathbf{g}}_{best}^{t+1}+|{\textbf{x}}_i^{t}-{\mathbf{g}}_{best}^{t+1}|A^{+}L, &{} \text { otherwise }\end{array}\right. \end{aligned},$$

(4)

where ${\mathbf{g}}_{worst}$ and ${\mathbf{g}}_{best}$ denote the current global worst and best positions, respectively, with the help of which the discoverers can improve the convergence speed of the algorithm, but it increases the risk of falling into a local optimum. $A^+=A^T(AA^T)^{-1}$, where A denotes a $1 \times D$ matrix with each element in it having a value randomly set to 1 or $-1$. Eq. (4) shows that $i>N/2$ indicates that scroungers need to fly elsewhere to get food; otherwise, scroungers get food form around producers.

Step 4:

Scouters are randomly selected from the swarm, typically 10–20% of the total swarm size, and they are updated as

$$\begin{aligned} {\textbf{x}}_i^{t+1}=\left\{ \begin{array}{ll}{\mathbf{g}}_{worst}^{t}+\beta |{\textbf{x}}_i^{t}+{\mathbf{g}}_{best}^{t}|, &{} \text{ if } f({\textbf{x}}_i^{t})>f({\mathbf{g}}_{best}^{t}) \\ {\textbf{x}}_i^{t}+K\left( \frac{|{\textbf{x}}_i^t+{\mathbf{g}}_{worst}^{t} |}{|f({\textbf{x}}_i^{t})-f({\mathbf{g}}_{worst}^{t})|+\sigma }\right) , &{} \text{ if } f({\textbf{x}}_i^{t})=f({\mathbf{g}}_{best}^{t})\end{array}\right. \end{aligned},$$

(5)

where $\beta$ takes a random value with normal distribution properties, K is a parameter that takes a random value between $-1$ and 1, $\sigma$ is a constant to avoid the occurrence of an error when the denominator is 0, and $f({\mathbf{g}}_{best}^{t})$ and $f({\mathbf{g}}_{worst}^{t})$ are fitness values of the current global best and worst individuals, respectively. The scouters take fitness according to an update criterion, i.e., $f({\textbf{x}}_i^{t})>f({\mathbf{g}}_{best}^{t})$ indicates that the sparrow is at risk of predation and needs to change its location according to the current best individual, whereas when $f({\textbf{x}}_i^{t})=f({\mathbf{g}}_{best}^{t})$, a sparrow needs to strategically move closer to other safe individuals to improve its safety index.

Step 5:

Updation and stopping guidelines are applied. The current position of a sparrow is only updated if its corresponding fitness is better than that of previous position. If the maximum number of current iteration is not reached, then return to Step 2; otherwise, output position and fitness of the best individual.

Thus, the basic framework of SSA is realized in Algorithm 1.

Chaotic maps

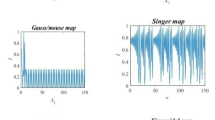
Chaos is defined as a phenomenon and exhibits some sort of chaotic behavior by using an evolution function and have three main characteristics: i) quasi-stochastic; ii) ergodicity; and iii) sensitivity to initial conditions⁶⁰. If its initial condition is changed, this may lead to a non-linear change in its future behavior. Thus, stochastic parameters in most algorithms can be strengthened by using chaos theory, given that the ergodicity of chaos can help explore the solution space more fully. Table 1 presents the mathematical expressions for the ten chaotic maps used in this study⁴⁴, where ${\tilde{x}}$ represents the random number generated from a one-dimensional chaotic map. Figure 1 shows their own visualizations, as well.

Table 1 Definition of the ten chaotic maps used in this study.

Figure 1

Visualizations of the ten chaotic maps used in this study and generated by using Matplotlib 3.5.2⁶¹ in Python 3.9.12⁶².

Proposed chaotic sparrow search algorithm (CSSA)

In this study, CSSA is produced by mitigating the deficiencies of SSA through chaotic maps in three aspects: i) initial swarm; ii) two random parameters; and iii) clamping the sparrows crossing the search space. The initial swarm of SSA is usually generated randomly, and swarm diversity is thus easily eventually lost, leading to a lack of extensive exploration of the solution space. This can be regularly amended throughout the iterative process by utilizing the ergodic nature of chaos. For the two random parameters, this study considers $\alpha$ in the producer (Eq. (3)) and K in the scouter (Eq. (5)). Since $\alpha \in [0,1]$, it is replaced clearly by any of the ten chaotic maps, conditioned that the Chebyshev and Iterative chaotic maps take absolute values. Also, $K \in [-1,1]$, so this study finally settles its replacement with the Chebyshev map. Finally, the position of sparrows going outside the search range is also clamped with the help of chaotic maps by redefining it as

$$\begin{aligned} x_{i,j}^{t}=\left\{ \begin{array}{ll} x_{i,j}^{t}, &{} \text { if } x_{i,j}^{t} \in [0,1] \\ {\tilde{x}}_{i,j}^{t}, &{} \text { otherwise }\end{array},\right. \end{aligned}$$

(6)

where $x_{i,j}^{t}$ and ${\tilde{x}}_{i,j}^{t}$, respectively, represent the original and chaotic positions of a sparrow i at a dimension j and an iteration t. By analyzing the experimental results in Section Comparative analysis, the final version of CSSA is eventually released with the following final configuration: (i) the Circle map is used to generate the initial swarm, replace $\alpha$ in Eq. (3), and relocate the sparrows crossing the search range via Eq. (6); and (ii) the Chebyshev map substitutes for K in Eq. (5).

Only using the best individuals in SSA to guide the evolutionary direction of its swarm improves its convergence speed but also increases the risk of falling into a local optimum. To address this issue, SSA sets some random numbers in the algorithm, but the random number generator used is not without sequential correlation in successive calls, so swarm diversity still decreases in the late iteration of the algorithm. The randomness and unpredictability of chaotic sequences can be then utilized in the generation of random numbers to enhance swarm diversity of SSA, thus increasing its exploration capability to scrutinize the search space more widely^63,64. Thus, this work uses chaotic maps to generate the initial swarm of SSA and replaces some random numbers in it.

Solution encoding

To our knowledge, binary vectors⁶⁵ are substantial to encode features in FS problems, and a facilitative scheme (e.g., transfer functions) can be used to convert the continuous search space into a binary one⁶⁶, in which 0s and 1s are used to organize the position of individuals. All features are initially selected, and during subsequent iterations, a feature is denoted as 1 if it is selected; otherwise, it is represented as 0. In this study, to construct the binary search space, CSSA is discretized by using a V-shaped transfer function⁶⁷ as

$$\begin{aligned} V\left( {\textbf{x}}_i^{t+1}\right) =\left|\frac{2}{\pi } \arctan \left( \frac{\pi }{2} {\textbf{x}}_i^{t+1}\right) \right|. \end{aligned}$$

(7)

Thus, the locations of SSA’s individuals are made up of binary vectors⁶⁸ as

$$\begin{aligned} x_{i,j}^{t+1}={\left\{ \begin{array}{ll}\lnot { x_{i,j}^{t} }, &{} \text { if } r < V\left( x_{i,j}^{t+1}\right) \\ x_{i,j}^{t}, &{} \text { otherwise }\end{array}\right. }, \end{aligned}$$

(8)

where $r \sim U{(0,1)}$. $r < V(\cdot)$ means that if a feature is previously selected, it is now discarded and vise versa; otherwise, a feature’s selection state is preserved.

Flow of CSSA

CSSA first builds an initial swarm using chaotic maps. Depending on the range of the chaotic maps, the initial point of the chaotic maps can take any value between 0 and 1, for example, the initial point of the Chebyshev and Iterative chaotic maps can take a value between −1 and 1. An initial value ${\tilde{x}}^{0}$ for a chaotic map may have a significant influence of fluctuation patterns on it. So, except for the Tent chaotic map where ${\tilde{x}}^{0}=0.6$, we utilize ${\tilde{x}}^{0}= 0.7$^43,69 for all chaotic maps. Each location of a sparrow represents a possibly viable solution conditioned by clamping inside the range [0, 1] for each of its dimensions.

Second, a determinant is required to assess the quality of each binarized solution we obtain. FS problems typically include two mutually exclusive optimization objectives, namely, maximizing classification accuracy and lowering selected feature size. Weighted-sum methods are extensively employed in this type of problem due to their straightforwardness and simplicity of implementation⁷⁰. We employ the weighted-sum approach in the fitness function to achieve a good trade-off between the two objectives as

$$\begin{aligned} Fit_i = \gamma Err_i + (1-\gamma ) \frac{\vert S_i\vert }{D}, \end{aligned}$$

(9)

where k-Nearest Neighbor (k-NN, $k=5$^31,54) and $Err_i$ represent the classification algorithm that is run on selected features in a solution i and the respective classification error rate, respectively. k-NN is commonly used in combination with meta-heuristics in classification tasks for solving FS problems due to its computational efficiency⁵⁴. $\vert S_i\vert$ represent the number of useful features CSSA has selected in i. A smaller feature selection ratio indicates that the algorithm has more effectively selected useful features. $\gamma$ represents a weighting coefficient, which is set to 0.99 according to existing studies^54,71.

Next, the position of sparrows is updated according to Eqs. (3), (4), and (5), provided that $\alpha$ and K are replaced with independent random values generated by a given chaotic map. This highly support the search agents of CCSA to more effectively explore and exploit each potential region of the search space.

Finally, CSSA terminates based on a predefined termination condition. For optimization problems, there are typically three termination conditions: (i) the maximum number of iterations is reached; (ii) a decent solution is obtained; and (iii) a predetermined time window. The first condition is used as the termination condition in this study. Overall, CSSA is realized in Algorithm 2. For the sake of simplicity, Fig. 2 depicts its flowchart, as well.

Figure 2

Flowchart of CSSA.

Computational complexity analysis

Feature selection based on wrapper methods evaluates the candidate subsets several times in the process of finding the optimal feature subset, which increases the complexity of the algorithm. Therefore, this section analyzes the overall complexity of CSSA in the worst case.

To facilitate the analysis of CSSA’s time complexity, Algorithm 2 is inspected step by step. In the initialization phase (Line 2), the position of N sparrows is initialized with $\mathcal{O}$(N) time complexity. In the main loop phase, the time complexity of binarization (Line 5), solution evaluation (Line 6), and updating positions and redefining variables going outside the bounds (Lines 10–21) is $\mathcal{O}$(N), $\mathcal{O}(N+N \log {N}+1)$, and $\mathcal{O}$(2N), respectively. Finally, finding the globally best individual (Line 6) has a time complexity of $\mathcal{O}(\log {N})$. Thus, the worst time complexity of CSSA can be defined as $\mathcal{O}(N)+\mathcal{O}(T((N+N+N \log {N}+1)+2N))+\mathcal{O}(\log {N})=\mathcal{O}(N)+\mathcal{O}(T(4N+N \log {N}+1))+\mathcal{O}(\log {N})=\mathcal{O}(TN \log {N})$. On the other hand, the space complexity of CSSA is measured by overhead imposed by it on memory, i.e., $\mathcal{O}$(ND).

Experimental results and discussion

Dataset description

In this study, experiments are conducted on eighteen UCI datasets listed in Table 2, covering different subject areas, including physics, chemistry, biology, medicine, etc⁷². Interdisciplinary datasets have advantages to evaluate the applicability of CSSA in multiple disciplines.

Table 2 Characteristics of eighteen UCI datasets.

Performance metrics

We mainly use four metrics to assess the overall performance of competitors, namely, mean fitness ($Mean_{Fit}$), mean accuracy ($Mean_{Acc}$), mean number of selected features ($Mean_{Feat}$), and mean computational time ($Mean_{Time}$) defined as

$$\begin{aligned} Mean_{Fit}= & {} \frac{1}{M}\sum _{k=1}^{M} Fit_*^{k}, \end{aligned}$$

(10)

$$\begin{aligned} Mean_{Acc}= & {} \frac{1}{M} \sum _{k=1}^{M} Acc_*^{k}, \end{aligned}$$

(11)

$$\begin{aligned} Mean_{Feat}= & {} \frac{1}{M}\sum _{k=1}^{M} \frac{\vert S_*^{k}\vert }{D}, \end{aligned}$$

(12)

$$\begin{aligned} Mean_{Time}= & {} \frac{1}{M}\sum _{k=1}^{M} Time_*^{k}, \end{aligned}$$

(13)

where $M=30$ is the maximum number of independent runs. $f_*^{k}$, $Acc_*^{k}$, $\vert S_*^{k}\vert$, and $Time_*^{k}$ respectively, denote the values of fitness, accuracy, selected feature size, and computational time (measured in milliseconds) for the globally best solution obtained at run k.

The smaller the values of $Mean_{Fit}$, $Mean_{Feat}$, and $Mean_{Time}$, the better the CSSA’s performance. In contrast, the higher the value of $Mean_{Acc}$, the greater the CSSA’s performance. The optimality of the results is validated by using the hold-out strategy, in which the training and test sets are realized by randomly dividing each dataset into two parts, with the training phase taking up 80% of the dataset and the testing phase taking up the remaining 20%⁷³. Due to the stochastic nature of meta-heuristic algorithms, they cannot be fully replicated, and the average results for each algorithm and single dataset are thus determined over 30 independent runs and realized as the final values for all metrics. Furthermore, we use W, T, and L to represent, respectively, the number of wins, ties, and losses for CSSA in comparison to its rivals across all datasets experimented. Although this may adequately measure the effectiveness of the proposed method, non-parametric statistical tests, such as Wilcoxon’s signed-rank test, Friedman’s rank test, and Nemenyi’s test, are also required to determine CSSA’s statistical significance over its rivals. They are more appropriate and safer than parametric tests since they assume some, if limited, comparability and do not require normal distributions or homogeneity of variance⁷⁴. The best overall performances are indicated in bold.

Comparative analysis

In this section, the $Mean_{Fit}$ of CSSA is compared and examined against the ten various chaotic maps listed in Table 1, in order to obtain the finest CSSA version ever. The $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$ are then calculated, and post-hoc statistical analysis is performed on the eighteen UCI datasets and three high-dimensional microarray datasets detailed in Tables 2 and 21, respectively, to see if CSSA has a competitive advantage over its well-known peers. CSSA is also compared to several state-of-the-art, relevant FS methods in the literature to put the acquired results into context. Furthermore, an ablation study is used to do convergence analysis and exploration-exploitation trade-off analysis. The experimental setting has an impact on the final results, and Table 3 summarizes the circumstances for all experiments. There are frequently multiple hyper-parameters in meta-heuristic algorithms, and their values highly affect the performance of the final results to some extent. In this work, all competitors’ algorithm-specific parameter settings match those recommended in their respective papers, with no parameter tuning⁷⁵. Table 4 only provides the parameters that are shared by all algorithms.

Table 3 General experimental settings.

Table 4 Common parameters for all experiments.

CSSA under different chaotic maps

In this section, the effectiveness of CSSA is investigated under different chaotic maps reported in Table 1 with an initial point ${\tilde{x}}^{0}=0.7$ for all chaotic maps to obey fluctuation patterns^43,69 and exceptionally ${\tilde{x}}^{0}=0.6$ for the Tent map subjecting to its judgment condition. Thus, the best version of CSSA can be released. K in Eq. (5) takes a random value in the range $[-1,1]$ and only the Chebyshev and Iterative maps can, among the ten chaotic maps, give a value in such a range. So, CSSA is separately experimented and results are recorded for the Chebyshev map instead of K and Iterative map instead of K in Tables 5 and 6, respectively. Since the other three improvements, i.e., generating the initial swarm, substituting for $\alpha$ in Eq. (3), and relocating transgressive sparrows, can be all amended by using random values in the range [0, 1], they can be clearly tested with the ten chaotic maps, conditioned that the Chebyshev and Iterative maps take absolute values. The $Mean_{Fit}$ in Eq. (10) is taken as a key metric in this experiment to measure the distinction between different versions of CSSA based on the ten chaotic maps. We further employ W*, T*, and L* to reflect the advantages and disadvantages of the CSSA’s twenty variants when comparing independently to SSA.

From Tables 5 and 6combined, when using the Sinusoidal map, for instance, to substitute for $\alpha$, the experimental results show that CSSA with the Chebyshev and Iterative maps replacing K does not perform effectively, with better results than SSA on only 5 and 4 datasets, respectively, indicating that the Sinusoidal map cannot improve SSA’s performance. Furthermore, “W|T|L” shows that the Sinusoidal map has neither wins nor ties on the eighteen datasets when compared to other maps. The experimental results of CSSA under other maps are relatively better than SSA on most datasets. Overall, the best results are obtained when CSSA performs better than SSA on a total of 17 datasets, as shown in Table 5. Thus, since we attempt to maximize the performance of SSA, this study takes the Chebyshev map instead of K and the Circle map for the other three improvements, in order to release the best CSSA variant ever based on chaotic maps.

Table 5 SSA versus CSSA under different chaotic maps in terms of $Mean_{Fit}$, where the Chebyshev map substitutes for K in SSA.

Table 6 SSA vs. CSSA under different chaotic maps in terms of $Mean_{Fit}$, where the Iterative map substitutes for K in SSA.

Contribution of chaos to SSA’s overall performance

Table 7 compares the proposed CSSA with SSA based on $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$. CSSA gains an outstanding $Mean_{Fit}$ advantage for a total of 17 datasets, and only underperforms SSA on the WineEW dataset. In terms of $Mean_{Acc}$, CSSA obtains the highest accuracy on 14 datasets and similarly for the other 4 ones. In terms of $Mean_{Feat}$, CSSA also outperforms SSA on most datasets. As for $Mean_{Time}$, CSSA relatively has less computational time over the majority of datasets. On the one hand, this implies that the chosen fitness function is able to integrate the role of accuracy and selected feature size in classification tasks. Furthermore, it shows that CSSA can balance the exploration and exploitation capabilities, shielding SSA from falling into local optimum.

Table 7 Comparison of CSSA and SSA.

Comparison of CSSA and its peers

This section compares CSSA with twelve well-known algorithms, including SSA, ABC, PSO, BA, WOA, GOA, HHO, BSA, ASO, HGSO, LSHADE, and CMAES, in order to determine whether CSSA has a competitive advantage over them. A brief description of compared algorithms is given in Table 8.

Table 8 Summary information about the twelve compared optimization algorithms.

Table 9 compares the $Mean_{Fit}$ of CSSA with that of its peers. The results show that CSSA obtains the smallest $Mean_{Fit}$ on 13 datasets and ABC, SSA, and CMAES perform relatively better on the remaining datasets. Thus, $Mean_{Fit}$ results show that CSSA holds its own merits for most datasets and can perform best in comparison to other rivals by adapting itself to classification tasks.

Table 9 Comparison of CSSA against its peers in terms of $Mean_{Fit}$.

Table 10 compares CSSA with other algorithms in terms of $Mean_{Acc}$. The comparison results illustrate that CSSA obtains the highest $Mean_{Acc}$ on 9 datasets, ties for the highest on 6 datasets, having thus an outstanding performance on a total of 15 datasets, while ABC solely have higher $Mean_{Acc}$ than CSSA on only 3 datasets: CongressEW, Exactly2, and Tic-tac-toe. On the other hand CMAES only performs better than CSSA on the Tic-tac-toe. This may be attributed to the complex nature of data in these datasets.

Table 10 Comparison of CSSA against its peers in terms of $Mean_{Acc}$.

Table 11 compares CSSA with its peers in terms of $Mean_{Feat}$. CSSA has the lowest number of features selected on 9 datasets, while the other 12 algorithms won only on 9 datasets. Noteworthily, ABC is second to CSSA in terms of only $Mean_{Fit}$ and $Mean_{Acc}$, but has no advantages in terms of $Mean_{Feat}$.

Table 11 Comparison of CSSA against its peers in terms of $Mean_{Feat}$.

Table 12 compares $Mean_{Time}$ of CSSA over other algorithms. LSHADE has the lowest $Mean_{Time}$ among all algorithms, but the algorithm performs poorly in other aspects such as $Mean_{Fit}$, $Mean_{Acc}$, and $Mean_{Feat}$. While ABC performs slightly better for these metrics, it has the longest run time, reaching almost three times the duration of CSSA. In addition, although the $Mean_{Time}$ of CSSA is in the middle of the range of all the algorithms compared, it has a lower time cost than standard SSA, as shown in Table 7). This shows that CSSA significantly improves the performance of SSA without increasing or even decreasing the time complexity of the algorithm. This is another aspect that demonstrates the advantage of CSSA over standard one.

Table 12 Results of CSSA compared to its peers in terms of $Mean_{Time}$.

Furthermore, Figs. 3 and 4 prove the stability of CSSA in terms of $Mean_{Acc}$ and $Mean_{Feat}$ in means of boxplots. As can be seen from Fig. 3, CSSA obtained higher boxplots on all datasets except Exactly2. On the other hand, CSSA has smaller box sizes on all datasets except PenglungEW, SonarEW, and SpectEW, indicating that CSSA is more stable in terms of $Mean_{Acc}$ compared to its peers. Figure 4 also shows that CSSA is able to achieve lower $Mean_{Feat}$ on most datasets, guaranteeing a lower size of the boxplots. Figure 5 shows $Mean_{Acc}$ and $Mean_{Feat}$ of all competitors. It can be seen that CSSA achieves the highest $Mean_{Acc}$ accompanied with the least $Mean_{Feat}$.

Figure 3

Boxplot of $Mean_{Acc}$.

Figure 4

Boxplot of $Mean_{Feat}$.

Figure 5

Bar chart of $Mean_{Acc}$ and $Mean_{Feat}$.

Convergence curves of all competitors

Aforementioned experimental results can effectively describe the subtle differences among competing algorithms, but we also need to control the algorithm as a whole. The convergence behavior of all competitors is further analyzed. Figure 6 visually compares the $Mean_{Fit}$ trace of all competitors for the eighteen datasets, where all results are the mean of 30 independent runs per each iteration. It is clear that CSSA is more effective compared to SSA on almost all datasets, exhibiting that the convergence of CSSA is more accelerated than that of its peers. For most datasets, CSSA is at the bottom of the convergence traces of all other eleven algorithms, indicating that CSSA holds a competitive advantage among its rivals in terms of rapid convergence while jumping out of the local optima. This may be due to the distinctive characteristics (especially ergodicity) of chaotic maps, which help cover the whole search space more conveniently. Thus, CSSA achieves better exploratory and exploitative behaviors than its peers.

Figure 6

Convergence curves of CSSA and its peers.

Statistical test and analysis

Although it is evident from the previous analysis that CSSA has significant advantages over its peers, further statistical tests of the experimental results are required to bring rigorousness in terms of stability and reliability analyses. In this study, we analyze whether CSSA has a statistically significant advantage over its peers based on a p-value by using the Wilcoxon’s signed-rank test at a 5% significance level⁷⁶. When p<0.05, this indicates a significant advantage of CSSA compared to its peers; otherwise, CSSA has a comparable effectiveness among all competitors.

Table 13 shows the results of the Wilcoxon’s signed-rank test for CSSA over other competitors in terms of $Mean_{Fit}$, where “+” represents the number of datasets on which CSSA has a significant advantage over its peers, “$\approx$” indicates that CSSA is comparable to the corresponding competing algorithm, and “−” represents the number of datasets on which CSSA works worse than the algorithm it is being compared against. From Table 13, it is clear that CSSA has outstanding advantages over PSO, BA, HHO, and ASO for all the eighteen datasets, and over SSA, HGSO, LSHADE, CMAES, GOA, BSA, WOA, and ABC on 7, 17, 17, 16, 16, 16, 15, 14, and 12 datasets, respectively. Thus, CSSA outperforms its peers significantly on most datasets.

Table 13 p-values of Wilcoxon’s signed-rank test on CSSA vs. its peers in terms of $Mean_{Fit}$.

In addition, we further measures the statistical significance of CSSA relative to other algorithms in terms of $Mean_{Fit}$ by Friedman’s rank test⁷⁷. Assuming that we take a significance level $\alpha =0.05$, Friedman’s rank test is measured as

$$\begin{aligned} \chi _{F}^{2}=\frac{12 N_{D}}{N_{A}(N_{A}+1)}\left( \sum _{k=1}^{N_{A}} R_{k}^{2}-\frac{N_{A}(N_{A}+1)^{2}}{4}\right) , \end{aligned}$$

(14)

which is undesirably conservative, and a better statistic is therefore derived as⁷⁸

$$\begin{aligned} F_{F}=\frac{(N_{D}-1) \chi _{F}^{2}}{N_{D}(N_{A}-1)-\chi _{F}^{2}}, \end{aligned}$$

(15)

where $N_{D}$ is the number of datasets, $N_{A}$ is the number of comparative algorithms, and $R_{k}$ is the average ranking of an algorithm k. Thus, we have $N_{D} = 18$, $N_{A} = 13$, and $R_{k}$ calculated from Tables 9, 10, 11, and 12. Table 14 shows $R_{k}$, $\chi _{F}^{2}$, and $F_{F}$ for all algorithms under our four evaluation metrics. $F_{F}$ obeys the F-distribution with degrees of freedom $N_{A}-1$ and $(N_{A}-1)(N_{D}-1)$. The calculation gives $F(12,204)=1.80$, and since all $F_{F}$ are greater than that value, there is a significant difference among the algorithms in favor of CSSA.

Table 14 Results of Friedman’s rank test on CSSA vs. its peers.

Friedman’s rank test alone is usually unable to compare the significance of the algorithms against each other. So, Nemenyi’s test is also conducted⁷⁴. This test essentially compares the difference between the average ranking of each algorithm with a critical difference CD. If the difference is greater than CD, it indicates that the algorithm with the lower ranking is superior; otherwise, there is no statistical difference between the algorithms. CD is calculated as

$$\begin{aligned} CD = q_{\alpha }\sqrt{\frac{N_{A}(N_{A}+1)}{6N_{D}}}, \end{aligned}$$

(16)

where $q_{\alpha }$ is calculated as 3.31, given that $N_{A}=13$ and the confidence level $\alpha =0.05$. Thus, $CD = 4.30$, and significant differences between two algorithms hold when the difference between their average ranking is greater than that value.

Figure 7 shows CD results for all competitors. Vertical dots indicate the average ranking of the algorithms, and the horizontal line segment starting with the point indicates the critical difference. A significant difference between the algorithms is represented by the absence of intersection of the horizontal line segments of the algorithms. As shown, CSSA performs best in terms of $Mean_{Fit}$, $Mean_{Acc}$ and $Mean_{Feat}$, but performs less well in terms of $Mean_{Time}$. CSSA intersects only SSA, ABC and WOA in terms of $Mean_{Fit}$ and only SSA, WOA and HHO in terms of $Mean_{Feat}$, indicating that CSSA is significantly different from most compared algorithms in terms of $Mean_{Fit}$ and $Mean_{Feat}$. On the other hand, Fig. 7b shows that CSSA is significantly different from PSO, BA, HHO, ASO, HGSO and LSHADE in terms of $Mean_{Acc}$, and Fig. 7d shows that there is no significant advantage in $Mean_{Time}$ for CSSA, but rather a significant advantage for LSHADE. Furthermore, there is a difference between CSSA and SSA though it is not significant. Overall, since the $Mean_{Fit}$ among all evaluation metrics can synthesize the ability of the algorithm to handle FS problems, Wilcoxon’s signed-rank test, Friedman’s rank test, and Nemenyi’s test show that CSSA has a satisfactorily significant performance over its peers.

Figure 7

Nemenyi’s test on CSSA against its peers in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$.

Merits of CSSA’s main components via an ablation study

In this experiment, five representative continuous benchmark functions are picked from the CEC benchmark suite to investigate the impact of the different improvements embedded into CSSA in terms of swarm diversity and convergence trace. Their characteristics and mathematical definitions are reported in Table 15.

Table 15 Five representative CEC benchmark functions with diverse characteristics.

Since CSSA is specifically proposed for FS problems, its search space is restricted to [0, 1] due to the existence of chaotic maps. However, in order to fully demonstrate the advantages of its main components, CSSA should be tested in different search spaces for diverse benchmark functions. Therefore, we further analyze CSSA in comparison to CSSA without chaotic initial swarm (NINICSSA), CSSA without chaotic random parameters (NPARCSSA), and CSSA without chaotic update of transgressive positions (NPOSCSSA). We define parameter settings in this experiment for all algorithms as: the maximum number of iterations is 100, swarm size is 30, and $D=50$ for Rosenbock, Ackley, and Rastrigin functions. All results are recorded as the mean of 30 independent runs.

Tables 16, 17, and 18 represent the experimental results of CSSA against NINICSSA, NPARCSSA, and NPOSCSSA on the eighteen UCI datasets, respectively. In general, CSSA outperforms other versions of CSSA in terms of $Mean_{Fit}$, $Mean_{Acc}$, and $Mean_{Feat}$, and it is also clear that CSSA has a significant advantage over NPOSCSSA, winning 16, 11, and 15 times in $Mean_{Fit}$, $Mean_{Acc}$, and $Mean_{Feat}$, respectively. On the other hand, it can be seen that, in terms of $Mean_{Time}$, CSSA has lower computational overhead compared to NINICSSA, NPARCSSA and NPOSCSSACSSA, due to the fact that chaotic map can generate random sequences more simply and efficiently. In short, it is clear that the three improvements proposed in this study are indispensable to boost the overall performance of CSSA, and redefining transgressive position by a chaotic map is especially important.

Table 16 Comparison of CSSA and NINICSSA in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$.

Table 17 Comparison of CSSA and NPARCSSA in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$.

Table 18 Comparison of CSSA and NPOCSSA in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$.

Furthermore, we study exploration merits added to CSSA thanks to its main components. We therefore take the average distance from the swarm center for all sparrows as a measurement of swarm diversity⁷⁹ as

$$\begin{aligned} {\mathscr {D}}=\frac{1}{N} \sum _{i=1}^{N} \sqrt{\sum _{j=1}^{D}\left( x_{i,j}-\dot{{\textbf{x}}}_{j}\right) ^{2}}, \end{aligned}$$

(17)

where $\dot{{\textbf{x}}}_{j}$ is the value at the j-th dimension of the swarm center $\dot{{\textbf{x}}}$. A larger ${\mathscr {D}}$ indicates that the greater the dispersion of individuals in the swarm the higher the swarm diversity, and conversely, the lower the swarm diversity.

Consequently, Fig. 8 compares CSSA with its ablated variants in terms of swarm diversity. As the algorithm gradually converges, individuals reach a similar state, leading to a convergence of the swarm to the minimum as the iterations proceed⁷⁹. It is obvious from Fig. 8 that SSA and NINICSSA always maintain the same swarm diversity on the Shekel function, indicating that the algorithm does not evolve and falls into a local optimum, while the other CSSA variants with chaotic initial swarm gradually converges, showing that initializing the swarm by a chaotic map facilitates the algorithm to jump out of the local optimum. The diversity curves of the remaining functions show that the diversity of NPOSCSSA remains basically the same as that of SSA, and it can be seen that swarm diversity of NPOSCSSA and SSA is high due to the presence of transgressive individuals. However, NPOSCSSA still has its own advantages over SSA. For example, NPOSCSSA converges normally on the Shekel function, indicating that although no updates are made to transgressive sparrows in this version, NPOSCSSA is still able to utilize chaotic maps in the initial swarm and random parameters to enable CSSA to escape from local optima. On the other hand, swarm diversity of NPARCSSA converged smoothly to the minimum point similarly to SSA. It is possible that, like SSA for the Shekel function, a similar situation occurs when NPARCSSA deals with more complex functions, but it is only because NPARCSSA retains chaotic initial swarm and chaotic position updates, i.e., it cannot thus find its deficiencies when the type of function being optimized is limited. In contrast, there is a clear trend in swarm diversity for CSSA when the initial swarm, transgression location, and random parameters are all amended by chaotic maps. In summary, each single improvement embedded into CSSA has its own merit and is indispensable for swarm diversity and avoidance of falling into local optima.

Figure 8

Swarm diversity curves.

From Fig. 9 CSSA have the ability of high exploration and low exploitation, so as to initially explore the solution space comprehensively, and as the iteration increases, the exploration ability of the algorithm gradually diminishes whereas the exploitation ability increase, so as to converge to the global optimal solution more quickly. As can be seen, the exploratory capability of all algorithms except CSSA in the initial phase of all five benchmark functions decreases sharply while the exploitation capability increases sharply. On the contrary, CSSA is able to maintain a decent trade-off by preserving high exploration capability in the initial stage and exploitation capability later, enabling the algorithm to explore the solution space more fully and search feasible regions to find the global optimal solution.

Figure 9

Exploration-exploitation trade-off curves.

Overall, Figs. 8 and 9 show that: (i) NPOSCSSA has similar performance to SSA but has the ability to avoid local optima, as shown in the test results of the Ackley and Shekel functions; (ii) NINICSSA has a risk of premature convergence but its convergence trend is fluctuating; (iii) NPARCSSA has a smooth convergence trend like SSA, which leads to the risk of the algorithm falling into a local optimum when dealing with more complex problems; and (iv) CSSA retains the above advantages while avoiding the shortcomings, allowing the algorithm to show the best results in terms of swarm diversity, and the balance between exploration and exploitation capabilities.

CSSA vs. other state-of-the-art optimizers in the literature

Table 19 compares CSSA with other algorithms in the literature, including hybrid evolutionary population dynamics and GOA (BGOA-EPD-Tour)⁸⁰, hybrid gravitational search algorithm (HGSA)⁸¹, improved HHO (IHHO)⁸², a self-adaptive quantum equilibrium optimizer with ABC (SQEOABC)⁸³, binary coyote optimization algorithm (BCOA)⁸⁴, chaotic binary group search optimizer (CGSO5)⁸⁵, and chaos embed marine predator algorithm (CMPA)⁸⁶.

In order to verify whether CSSA has a competitive advantage over similar algorithms, two recently proposed chaotic algorithms, i.e., CGSO5 and CMPA, are chosen among compared algorithms. From Table 19, $Mean_{Acc}$ of CSSA is higher than that of CGSO5 and CMPA on all datasets, except for the CongressEW dataset where it is inferior to CMPA. In addition, the comparison results with other non-chaotic algorithms also show that CSSA has outstanding advantages. In a summary, a comparison with FS literature works demonstrates usefulness and superiority of CSSA over other several, state-of-the-art methods.

Table 19 $Mean_{Acc}$ of CSSA compared to other optimizers in the literature.

CSSA on high-dimensional microarray datasets: The additional experiment

To verify the scalability and robustness of CSSA to tackle FS problems, we further test three high-dimensional microarray datasets having up to 12000 features, namely, 11_Tumors, Brain_Tumor2 and Leukemia2. They are all of high feature size, low sample size, as reported in Table 21. Since high-dimensional data can cause significant time overhead, we prefer to use the experimental settings in Table 20. Tables 22, 23, 24, and 25 show the experimental results in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$, respectively. It is evident that CSSA has outstanding advantages over other algorithms in terms of $Mean_{Fit}$ and $Mean_{Acc}$, but its performance in terms of $Mean_{Feat}$ is relatively poor, which can be justified by the high $Mean_{Acc}$ obtained. On the other hand, all algorithms have a huge overhead in terms of $Mean_{Time}$, which is normally caused by the limitations of the wrapper-based methods themselves. This can be improved by combining other methods (e.g., filter-based methods).

Table 20 Special settings for high-dimensional data experiments.

Table 21 High-dimensional microarray datasets.

Table 22 Comparison of CSSA against its peers in terms of $Mean_{Fit}$ on high-dimensional datasets.

Table 23 Comparison of CSSA against its peers in terms of $Mean_{Acc}$ on high-dimensional datasets.

Table 24 Comparison of CSSA against its peers in terms of $Mean_{Feat}$ on high-dimensional datasets.

Table 25 Comparison of CSSA against its peers in terms of $Mean_{Time}$ on high-dimensional datasets.

Discussion

In order to cope with issues encountered in standard SSA, such as early loss of swarm diversity and hence easily falling into local optima, this study integrates chaotic maps into SSA to produce CSSA. The effectiveness of CSSA has been demonstrated through many comparative and analytical studies. The main purpose of this section is to give a brief summary of the strengths and weaknesses of CSSA.

CSSA has the following advantages:

• 1. The improvement effect of ten chaotic maps on SSA is researched completely in this work, and thus the degree of contribution of diverse chaotic maps is examined from a global perspective. The best CSSA determined in this manner can avoid the one-sidedness of a single chaotic map and serve as a reference for subsequent research.

• 2. CSSA improves the performance of SSA while reducing its computational cost. From Table 7, it can be seen that CSSA significantly improves the performance of the algorithm in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$ without highly increasing the computational cost.

• 3. Tables 9, 10, 11, and 12 describe in detail the results of CSSA compared with twelve well-known algorithms in terms of $Mean_{Fit}$, $Mean_{Acc}$, $Mean_{Feat}$, and $Mean_{Time}$. Figures 3, 4, and 5 visualize the classification accuracy and feature reduction rate performance of all competitors. It can be seen that CSSA effectively reduces the $Mean_{Feat}$ (0.4399) while achieving the highest $Mean_{Acc}$ (0.9216). In addition, CSSA’s ability to handle truly high-dimensional data has been demonstrated through experiments on three microarray datasets with up to 12000 features.

• 4. Furthermore, seven recently proposed methods selected from the literature are compared with CSSA, and the comparative study shows that our proposed method not only outperforms other non-chaotic algorithms but also has outstanding advantages among similar chaotic ones.

In addition, CSSA has its own limitations:

• 1. Table 12 demonstrates that CSSA is not optimal in terms of $Mean_{Time}$, which may be due to the fact that SSA was originally developed for continuous search space. Although the V-shaped function in Eq. (7) allows CSSA to deal with discrete problems, its essence is still evolving via a continuous approach. As a result, to improve overall performance and reduce computational costs, a more efficient SSA variant for discrete problems can be designed.

• 2. It is vital to note that CSSA cannot successfully minimize the $Mean_{Feat}$ when dealing with extremely high-dimensional data. Table 24 demonstrates that CSSA picks more than 5000 features (a nearly 50% reduction) on all three datasets, indicating that the algorithm cannot successfully reduce selected feature size and is not conducive to the analysis and extraction of valuable features. This issue can be overcome by combining the filters (which are used to reduce and select high-quality features) and wrappers (which are used to improve the algorithm’s performance). CSSA, on the other hand, achieves superior superior $Mean_{Fit}$ and $Mean_{Acc}$, as seen in Tables 22 and 23, respectively.

Conclusion

In this paper, a new chaotic sparrow search algorithm (CSSA) is suggested and used to FS problems. The majority of the literature focuses on the influence of a single chaotic map on an algorithm. Ten chaotic maps are investigated in this study comprehensively. Based on our findings, CSSA with Chebyshev and Circle chaotic maps embedded into it delivers the best outcomes among evaluated schemes by making a good trade-off between exploration and exploitation in CSSA. CSSA offers a competitive edge in global optimization and addressing FS problems when compared to twelve state-of-the-art algorithms, including LSHADE and CMAES, and seven recently proposed, relevant approaches in the literature, according to comparative research. Furthermore, a post-hoc statistical analysis confirms CSSA’s significance on most UCI datasets and high-dimensional microarray datasets, demonstrating that CSSA has an exceptional ability to pick favorable features while achieving high classification accuracy.

However, when dealing with high-dimensional datasets, CSSA’s time cost is not satisfactory when compared to its contemporaries, and the feature selection ratio is not successfully reduced. To address these concerns, we propose to integrate the filters and wrappers in future work, in order to leverage their respective benefits in building a new binary SSA version that is more suitable for high-dimensional FS problems.