Introduction

Newtonian or non-Newtonian fluids are used by researchers, modellers, and physiologists at the early age as they do in many technical and medical sectors. By examining the behaviour of non-Newtonian distributions, they can apply engineering for oil reservoirs, material processing, and food production. A single relationship cannot be used to categorise all Newtonian liquids because to their disparate characteristics. Researchers have recently concentrated their attention on understanding how Newtonian or non-Newtonian fluids are utilised in the presence of nanoparticles. Implementations in the biomedical field, rheumatoid arthritis, digestive system, and oil refinement are a few examples1,2,3,4. The peristaltic transport of a Carreau fluid in a compliant rectangular duct was investigated by Riaz et al.5. Akram et al.6 demonstrate the effects of MHD hybrids on the thermal convection of Prandtl nanofluid flow. Other researchers investigate and discuss Newtonian and non-Newtonian nanofluid applications7,8,9,10,11,12,13,14,15,16,17,18,19.

Due to the importance of calculation in most phases, petrochemical chemicals and ink are two examples of fluids with variable viscosity. We agreed that fluid characteristics can alter in a suggestive way because of temperature variations. Investigational facts demonstrate, as an example, that the viscosity of water as represented in Table 1. The issue of peristaltic flow of a fluid with varying viscosity via a tube was examined by Eldabe et al.20. They also investigated the tube's centerline trapping phenomenon. By Nadeem et al.21, the effect of heat transfer in peristalsis with a viscosity of non-constant temperature is discussed. The peristaltic flow of non-constant viscosity in the presence of a chemical reaction was researched by Asghar et al.22. Eldabe et al.23 explore how a chemical reaction, nonconstant viscosity, and Ohmic dissipation affect the peristaltic motion of a pseudoplastic nanofluid.

Table 1 Values of water dynamical viscosity with temperature.
Full size table

Nanoparticles and a carrier liquid are combined to form nanofluid. In addition, the fluid with nanoparticles has numerous engineering and technological applications, such as vehicle thermal management, vehicle cooling, heat exchangers, nuclear reactors, electronic device cooling, etc. In addition, the base fluid is typically a conductive fluid like oil, water, or ethylene glycol, and the nanoparticles are typically comprised of metals or non-metals. Thermal conductivity is higher for solid metals than for primary liquids. Suspended nanoparticles can thereby enhance thermal conductivity and heat transfer efficiency. Choi24 is credited with introducing the idea of nanofluids. Using a nanoparticle solution above a stretchable shape, Shafiq et al.25 investigated the issue of chemically reacting bioconvective of second-grade liquid. There are more studies26,27,28,29,30,31,32,33,34,35 that support further investigation in this area.

As a result of the investigations indicated above, the primary goal of this study is to present a new generalisation model for entropy generation and the impacts of changing viscosity parameters on the MHD peristaltic flow of biofluids. The peristaltic flow of Newtonian fluid is thought to be modelled by the blood flow through arterial catheterization. We made the long-wavelength and low-Reynolds number assumptions. Analytically approximating solutions to the momentum, energy, and nanoparticle concentration equations have been found using the homotopy analysis technique. Findings are graphically displayed and explained for various flow parameter problems. The gastric juice flow in the small intestine when an endoscope is placed is one physiological flow where this physical modelling is crucial.

Problem formulation

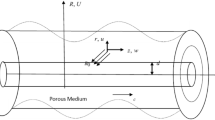
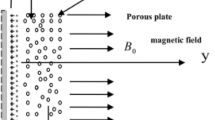
Between two coaxial tubes and a porous media, we investigated the flow of Newtonian fluid. The transverse magnetic field B0 in the fluid is meant to be constant. While the outer tube's wall is being waved by a sinusoidal wave, the inner tube is rigid and homogenous. We employ the cylindrical coordinate system (r, θ, z). The inner and outer tube equations are as follows:

$$r_{{1}} = a,\;r_{2} = H = d + b\sin \frac{2\pi }{\lambda }(z - ct).$$
(1)

The equations that govern the flow are the balance of mass

$$\nabla \cdot \underline {V} = \, 0,$$
(2)

the equation of momentum

$$\rho (\underline{V} \cdot \nabla \underline{V} ) = - \nabla P + \nabla \cdot \underline{\tau } - \frac{{\mu_{B} }}{{k_{p} }}\underline{V} + \underline{J} \times \underline{B} ,$$
(3)

the equation of energy

$$\rho c_{p} (\underline{V} \cdot \nabla T) = k\nabla^{2} T - \nabla .\underline{q}_{r} + D_{T} \,\left( {\nabla T} \right)^{2} + D_{B} \,\left( {\nabla T} \right)\left( {\nabla C} \right),$$
(4)

the equation of concentration

$$(\underline{V} \cdot \nabla C) = D_{B} \,\nabla^{2} C + \frac{{D_{T} }}{{T_{2} }}\,\nabla^{2} T,$$
(5)

Maxwell’s equations

$$\nabla \times \underline{B} = \mu_{e} \underline{J} ,\,\nabla \cdot \underline{B} = 0,\;\nabla \times \underline{E} = 0,\;\nabla \cdot \underline{J} = 0$$
(6)

and Ohm’s law

$$\underline{J} = \sigma \,\left( {\underline{E} + \underline{V} \times \underline{B} } \right),$$
(7)

The governing equations for an incompressible flow in the fixed wave are given as36,37,38

$$\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0,$$
(8)
$$\begin{aligned} \rho \left( {u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}}} \right) & = - \frac{\partial P}{{\partial r}} + \frac{\partial }{\partial r}\left( {2\mu (r,z)\frac{\partial u}{{\partial r}}} \right) + \frac{\partial }{\partial z}\left( {\mu (r,z)\left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)} \right) \\ & \quad - \frac{2\mu (r,z)}{r}\left( {\frac{\partial u}{{\partial r}} - \frac{u}{r}} \right) - \left( {\sigma B_{0}^{2} + \frac{\mu (r,z)}{K}} \right)u, \\ \end{aligned}$$
(9)
$$\begin{aligned} \rho \left( {u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}}} \right) & = - \frac{\partial P}{{\partial z}} + \frac{\partial }{\partial z}\left( {2\mu (r,z)\frac{\partial w}{{\partial z}}} \right) + \frac{1}{r}\frac{\partial }{\partial r}\left( {r\mu (r,\,z)\left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)} \right) \\ & \quad - \left( {\sigma B_{0}^{2} + \frac{\mu (r,z)}{K}} \right)w, \\ \end{aligned}$$
(10)
$$\begin{aligned} \left( {u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}}} \right) & = \frac{k}{{\rho c_{p} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) - \frac{1}{{\rho c_{p} r}}\frac{{\partial (rq_{r} )}}{\partial r} + \frac{{\sigma B_{0}^{2} }}{{\rho c_{p} }}\left( {u^{2} + w^{2} } \right) + \\ & \quad + D_{T} \left( {\nabla T} \right)^{2} + D_{B} \left( {\nabla T} \right)\left( {\nabla C} \right) + Q_{0} \left( {T - T_{2} } \right), \\ \end{aligned}$$
(11)
$$u\frac{\partial C}{{\partial r}} + w\frac{\partial C}{{\partial z}} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}} + \frac{{\partial^{2} C}}{{\partial z^{2} }}} \right) + \frac{{D_{T} }}{{T_{2} }}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right).$$
(12)

The boundary conditions are given by:

$$u = 0,\,w^{\prime } = 0,\,T = T_{1} ,\,C = C_{1} \;{\text{at}}\;r = r_{1} .$$
(13)
$$u = - \frac{\partial H}{{\partial z}},\,w = - c,\,T = T_{2} ,\,C = C_{2} \;{\text{at}}\;r = r_{2} ,$$
(14)

By using the Rosseland approximation39,40, the radiative heat flux is given by:

$$q_{r} = \frac{{ - 4\sigma^{ * } }}{{3k_{R} }}\frac{{\partial T^{4} }}{\partial r}.$$
(15)

The temperature differences within the flow are small, such that T4 may be expressed as a linear function of temperature. This is accomplished by expanding T4 in a Taylor series about T2 and neglecting higher-order terms, one gets:

$$T^{4} \approx 4T_{2}^{3} T - 3T_{2}^{4} .$$
(16)

The appropriate non-dimensional variables for the flow are defined as

$$\begin{gathered} r^{ * } = \frac{r}{d},\;z^{ * } = \frac{z}{\lambda },\;u^{ * } = \frac{\lambda }{cd}u,\;w^{ * } = \frac{w}{c},\;P^{ * } = \frac{{d^{2} }}{{\lambda c\mu_{0} }}P,\;T^{*} = \frac{{T - T_{2} }}{{T_{1} - T_{2} }}, \hfill \\ \delta = \frac{d}{\lambda },\;C^{*} = \frac{{C - C_{2} }}{{C_{1} - C_{2} }},\;t^{ * } = \frac{c}{\lambda }t,\;h = \frac{H}{d},\;\varepsilon = \frac{b}{d},\;{\text{Re}} = \frac{\rho cd}{{\mu_{0} }},\;\mu^{*} = \frac{\mu }{{\mu_{0} }}. \hfill \\ \end{gathered}$$
(17)

In terms of these variables, dropping the star mark for simplicity and considering long wavelength and low-Reynolds number approximation, Eqs. (8–12) become:

$$\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0,$$
(18)
$$\frac{\partial P}{{\partial r}} = 0,$$
(19)
$$\frac{\partial P}{{\partial z}} = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\,\mu (r,\,z)\frac{\partial w}{{\partial r}}} \right) - \left( {M^{2} + \frac{\mu (r,\,z)}{{Da}}} \right)w,$$
(20)
$$\left( {\frac{3 + 4R}{{3\Pr }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}}} \right) + Ec\;M^{2} \;w^{2} + Nt\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + Nb\left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}}} \right) = 0,$$
(21)
$$\frac{{\partial^{2} C}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial C}{{\partial r}} + \frac{Nt}{{Nb}}\,\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}}} \right) = 0.$$
(22)

Thus, the boundary conditions (13) and (14) in their dimensionless form are transformed into:

$$w^{\prime } = 0,\;T = C = 1,\;{\text{at}}\;r = \varepsilon .$$
(23)
$$w = - 1,\;T = C = 0\;{\text{at}}\;r = h = 1 + \varepsilon \sin 2\pi z.$$
(24)

The following formula, Eldabe et al.20 and Lachiheb41, considers the fluid viscosity based on both radial and axial components:

$$\mu (r,\,z) = \mathop e\nolimits^{ - \alpha r/h(z)} .$$
(25)

This choice is induced by the following physiological phenomena42:

  1. (1)

    The chyme viscosity is affected by a excretion of liquids plenty. The latter consists mainly of water and acids and is injected into the intestine lumen from the wall.

  2. (2)

    During the blood transport in the arteries and blood-vessels, the white blood cells and plasma are precipitated in the center while the red blood cells are piled in the boundaries of the wall, resulting in a decrease in the value of the viscosity at the points more closer to the wall.

For \(\alpha \, \ll \,\) 1, the formula (19) will tend to the following relation

$$\mu (r,\,z) = 1 - \alpha r/h.$$
(26)

Morever, the viscosity in the variable case is the viscosity of the base fluid, there are also micro-organism particles present inside the fluid called nanoparticles which are known as the fluid mixture or nanofluid. So, the variable viscosity presented in the current paper of the base fluid depends on the place only, and not the temperature, which means that the thermal physical properties in this study will not change in the presence of both Brownian and the thermophoresis effect. This is because the Brownian motion and the thermophoresis coefficient are not defined by the variable viscosity parameter.

In other side, there are many papers which take the variable viscosity case without considering variable thermophysical properties of the model21,22,23,41.

Equations (14), (15) and (16) are highly non-linear ordinary differential equations. If Da = M = 0 and in the absence of heat and mass transfer, this study tends to the work of Eldabe et al. 20.

Entropy generation analysis

The dimensionless entropy generation can be written as follows33:

$$Eg = \left( {\frac{\partial T}{{\partial r}}} \right)^{2} + \left( {\frac{3\Pr }{{3 + 4R}}} \right)\,\left( {EcM^{2} w^{2} + Nt\left( {\frac{\partial T}{{\partial r}}} \right)^{2} + Nb\left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}}} \right)} \right),$$
(27)

The ratio between heat transfer entropy to total entropy is defined by Bejan number Bn.

Method of solution

Exact solution

The exact solutions of Eq. (20) with boundary conditions (23) and (24), can be written as

$$\begin{aligned} w(r,z) & = a_{1} r + a_{2} r^{2} + (a_{3} + a_{7} r)\ln r + (a_{4} + a_{6} r)\ln (h - a_{5} r) \\ & \quad + a_{8} \ln (h - (a_{5} - 1)r) + a_{9} Li_{2} \left( {\frac{{a_{5} r}}{h}} \right) + a_{10} , \\ \end{aligned}$$
(28)

where \(Li_{n} \left( z \right)\) is the polylogarithm function, which is defined by

$$Li_{n} \left( z \right) = \frac{{( - 1)^{n - 2} }}{(n - 2)!}\int\limits_{0}^{1} {(\ln (t))^{n - 2} } \ln (1 - zt)dt,$$
(29)

Homotopy perturbation method

The homotopy perturbation technique is a useful method, which can treat many kinds of differential equations systems because it requires only a few steps to obtain semi-analytical solutions for these systems. In addition, it is a combination of the perturbation method and the homotopy analysis method. One of the most important steps in the homotopy perturbation method is to guess an initial solution. Following43,44,45,46,47, Eqs. (21) and (22) can be rewritten as follows:

$$\begin{aligned} H(p,T) & = L(w) - L(w_{10} ) + pL(w_{10} ) + p\left( {\frac{3\Pr }{{3 + 4R}}} \right)\left( {EcM^{2} w^{2} + Nt\left( {\frac{\partial T}{{\partial r}}} \right)^{2} } \right. \\ & \quad \left. { + Nb\left( {\frac{\partial T}{{\partial r}}\frac{\partial C}{{\partial r}}} \right)} \right), \\ \end{aligned}$$
(30)
$$H(p,C) = L(C) - L(C_{10} ) + pL(C) + p\left( {\frac{Nt}{{Nb}}\left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}}} \right)} \right).$$
(31)

With the linear operator. The initial approximations \(T_{10}\) and \(C_{10}\) can be written as

$$T_{10} = C_{10} = \frac{{\ln r - \ln r_{2} }}{{\ln r_{1} - \ln r_{2} }}.$$
(32)

Now, we assume that:

$$(T,C) = (T_{0} ,C_{0} ) + p(T_{1} ,C_{1} ) + p^{2} (T_{2} ,C_{2} ) + \cdots .$$
(33)

Substituting from (33) into (30) and (31), we get the solutions of these equations as:

$$\begin{aligned} T(r,z) & = \frac{{\ln \left( {r/r_{2} } \right)}}{{\ln \left( {r_{1} /r_{2} } \right)}} + a_{11} r + a_{12} r^{2} + a_{13} r^{3} + a_{14} r^{4} + (a_{15} + a_{16} r + a_{17} r^{2} + a_{18} r^{3} ) \\ & \quad \times \ln r + a_{19} r^{2} \left( {\ln r} \right)^{2} + (a_{20} + a_{21} r + a_{22} r^{2} + a_{23} r^{3} )\ln (h - a_{5} r) + \\ & \quad + (a_{24} + a_{25} r^{2} )\ln (h - (a_{5} - 1)r) + (a_{26} + a_{27} r^{2} + a_{28} \ln \frac{{a_{5} r}}{h}) \\ & \quad \times \left( {\ln (h - a_{5} r)} \right)^{2} + a_{29} \ln ((a_{5} + 1)r - h) + \left( {a_{30} + a_{31} \ln r} \right)Li_{2} \left( {\frac{{a_{5} r}}{h}} \right) \\ & \quad + a_{32} \ln (h - a_{5} r)Li_{2} \left( {1 - \frac{{a_{5} r}}{h}} \right) + a_{33} Li_{3} \left( {\frac{{a_{5} r}}{h}} \right) + a_{34} Li_{3} \left( {1 - \frac{{a_{5} r}}{h}} \right), \\ \end{aligned}$$
(34)
$$C(r,z) = \frac{{\ln \left( {r/r_{2} } \right)}}{{\ln \left( {r_{1} /r_{2} } \right)}} + a_{35} + a_{36} \ln r - \frac{Nt}{{Nb}}T_{1} (r,z),$$
(35)

Convergence of homotopy perturbation method

Assume that the solution of Eqs. (21) and (22) can be written as a power series as follows

$$n(r,P) = n_{{^{0} }} + Pn_{{^{1} }} + P^{2} n_{{^{2} }} + \cdots .$$
(36)

where n is one of the physical quantities T and C. Setting \(P = 1\) we obtain the semi-analytical solution of Eqs. (21) and (22) as follows:

$$n = \mathop {Lim}\limits_{P \to 1} \left( {n^{0} + Pn^{1} + P^{2} n^{2} + \cdots } \right).$$
(37)

The series of Eqs. (21) and (22) are convergent for most of all cases.

The dimensionless volume flow rate, in the fixed frame, is given by

$$Q(z,t) = 2\int_{0}^{h} {rw\,dr} ,$$
(38)

Now, Nusselt number Nu and Sherwood number Sh are defined, respectively, by

$${\text{Nu}} = \left. {\frac{\partial \theta }{{\partial r}}} \right|_{r = h} \;{\text{Sh}} = \left. {\frac{\partial C}{{\partial r}}} \right|_{r = h} .$$
(39)

The expressions for Nu and Sh have been calculated by substituting from Eqs. (34) and (35) into Eq. (39) respectively, and they have been evaluated numerically for several values of the parameters of the problem, using the software Mathematica package. The obtained results will be discussed in the next section.

Results and discussion

In our study, we assumed that the viscosity coefficient varies with both radial coordinate r and axial coordinate z; moreover, long wavelength and small Reynolds number assumptions restricted our work, while the wave number is neglected. The default values of problem-related parameters are taken as:

$$\begin{gathered} Pz = 0.1, \alpha = 0.3, M = 15, {\text{Da}} = 0.1, R = 1, {\text{Ec}} = 0.2, \Pr = 4.5, Nt = 3.5, \hfill \\ Nb = 1.5, r1 = 0.3, z = 0.8, \varepsilon = 0.1. \hfill \\ \end{gathered}$$

The following values of human small intestine parameters are used48

$$d = 1.2 {\text{cm}}, c = 2 {\text{cm}}/{\text{min}}, \;\lambda = 8.1 {\text{cm}}.$$

In Fig. 1, a three-dimensional graph is drawn to illustrate the effects of radial coordinate r and axial coordinate z on the axial velocity w. We observed from this figure that the axial velocity w increases with increasing z, while it decreases as r increases. The parameter of viscosity \(\user2{ }\alpha\) is affected by the combination of some materials such as crude oil, the temperature, dissolved gas content, and pressure. The viscosity parameter will decrease, when temperature increases, as a result, viscosity measurements are always reported with the temperature at which the measurement is made. The effects of the viscosity parameter \(\alpha\) and Darcy number Da on the axial velocity w which is a function of the radial coordinate r are shown in Figs. 2 and 3, and it is shown that the axial velocity w increases by increasing \(\alpha\), and the axial velocity increases with r, with a relationship that seems like a parabola. While the axial velocity w decreases as Da increases as given in Fig. 3. The following clarifies the result in Fig. 2; due to the relation in Eq. (19), it is found that the increment of the viscosity parameter will help the fluid to move easier. Similarly, if we draw the variation of w with r for different values of the radiation parameter R, we will obtain a figure in which the behavior of the curves is the same as that obtained in Fig. 3, except that the obtained curves are very close to those obtained in Fig. 3, but this figure will not be given there to save space.

Figure 1
figure 1

Three-dimensional axial velocity is plotted versus r and z.

Full size image
Figure 2
figure 2

The axial velocity w is plotted with r, for different values of \(\alpha\).

Full size image
Figure 3
figure 3

The axial velocity w is plotted with r, for different values of Da.

Full size image

Thermophoresis or thermo-migration is an original sin that occurs in a blend of transported particles, where the different particle types display different echoes to the temperature gradient force. The effects of the thermophoresis parameter Nt and radiation parameter R on the temperature distribution T which is a function of r are shown in Figs. 4 and 5, respectively. It is clear from these figures that the temperature distribution is always negative, and it increases by increasing Nt, while it decreases as R increases. It is also noted that for each value of both Nt and R, there exists a maximum value of T, which its value increases by increasing Nt and decreases by increasing R, and all maximum values occur at. Similar results can be obtained, as in Fig. 4, by drawing T versus r for various values of Brownian motion parameter Nb, but the figure is not given here to save space. the result in Fig. 5 agrees with the physical expectation and previous definition and agrees with those which are presented by49.

Figure 4
figure 4

The temperature distribution T is plotted with r, for different values of Nt.

Full size image
Figure 5
figure 5

The temperature distribution T is plotted with r, for different values of R.

Full size image

Equation (29) evaluates how the nanoparticles concentration distribution C changes with the radial coordinate r. The effects of axial coordinate z and the dimensionless wave amplitude \(\varepsilon\) on the nanoparticles concentration distribution C are given in Figs. 6 and 7, respectively. It is found that the nanoparticles concentration increases by increasing z, but it decreases as \({\varvec{\varepsilon}}\) increases. Furthermore, the nanoparticles concentration is always positive and for large values of \({\varvec{\varepsilon}}\) and small values of z, the relation between C and r is a straight line. The effects of other parameters are similar to those obtained in Figs. 6 and 7.

Figure 6
figure 6

The nanoparticles concentration C is plotted with r, for different values of z.

Full size image
Figure 7
figure 7

The nanoparticles concentration C is plotted with r, for different values of \(\varepsilon\).

Full size image

Figure 8 and 9 give the influence of Eckert number Ec, and radiation parameter R on entropy generation Eg, respectively. Therefore, in these figures the Eq. (27) is evaluated by setting z = 0.8 and entropy generation is plotted versus the radial coordinate r. It is noted from these figures that entropy generation increases with the increase of Ec, whereas it decreases as R increases. It is also noted that the entropy generation for different values of Ec and R becomes lower with increasing r and reaches a minimum value (at a finite value of r : r = r0) after which it increases. The following clarifies the viscous dissipation effect on entropy generation, namely, the result in Fig. 8. Moreover, all curves for different values of Ec and R intersect at this minimum value. It is well known that the influence of dissipation produces heat due to traction between the particles of fluid, this supplementary heat is a reason for the increase of initial entropy of fluid. This increase in entropy generation causes an additional increment of the force of buoyant. As the buoyant force increases, the fluid velocity increases. So, the bigger traction between the particles of fluid and consequently bigger viscous heating of the fluid. Figure 10 shows the variation of the entropy generation Eg with r for various values of viscosity parameter \(\alpha\). It is seen from Fig. 10, that the entropy generation increases with the increase near the outer tube, namely, in the interval r ∈ [0.62, 0.7]; otherwise, it decreases by increasing \(\alpha\). Therefore, the behavior of Eg in the interval r ∈ [0.62, 0.7] is opposite to its behavior in the interval r ∈ [0, 0.62]. The effect of the dimensionless wave amplitude \(\varepsilon\) on entropy generation is illustrated in Fig. 11. It is found that the effect of \(\varepsilon\) on Eg is opposite to the effect of \(\alpha\) on Eg given in Fig. 10, with the only difference that, the curves in Fig. 10 are very close to those to each other in the second interval than those obtained in Fig. 11 The other figures are excluded here to save space.

Figure 8
figure 8

The entropy generation Eg is plotted with r, for different values of Ec.

Full size image
Figure 9
figure 9

The entropy generation Eg is plotted with r, for different values of R.

Full size image
Figure 10
figure 10

The entropy generation Eg is plotted with r, for different values of \(\alpha\).

Full size image
Figure 11
figure 11

The entropy generation Eg is plotted with r, for different values of \(\varepsilon\).

Full size image

Table 2 presents numerical results for Nusselt number Nu and Sherwood number Sh for various values of the dimensionless wave amplitude and Brownian motion parameter Nb. It is found from Table 2 that an increase in \({\varvec{\varepsilon}}\) decreases the values of both Nu and Sh. While an increase in Nb gives an opposite behavior to \({\varvec{\varepsilon}}\) in the case of Sh. Moreover, the results in a Table 2 are in agreement with those obtained by 20.

Table 2 Values of Nu and Sh for various values of \(\varepsilon\) and Nb.
Full size table

Conclusion

In this paper, the influences of both variable viscosity and wave amplitude on MHD peristaltic flow of Newtonian fluid between two co-axial cylinders under the consideration of long wavelength and the law-Reynolds number have been studied. In our analysis, we are taking into account the effects of both porous medium, Ohmic dissipation, and radiation. The analytical expressions are constructed for the velocity, temperature and nanoparticles concentration distributions. The present analysis can avail as a model which may help in understanding the mechanics of physiological flows50,51,52. The effects of various pertinent parameters on the flow are discussed through numerical computations. The main findings can be summarized as follows:

  1. (1)

    The axial velocity w decreases with the increase in each of \(\varepsilon\), R and Da, whereas it increases as \(\alpha\), Pr and M increase.

  2. (2)

    All curves of the axial velocity w for different values of \(\alpha\), R, Da, \(\varepsilon\), Pr and M don’t intersect at the boundary of the inner tube, then decrease with increasing r and they intersect at the boundary of the outer tube.

  3. (3)

    The temperature increases with the increase each of Pr, Nt, Nb and Ec whereas it decreases as both R and \(\varepsilon\) increase.

  4. (4)

    By increasing the radial coordinate r, the temperature T for different values of problem physical parameters becomes greater and ends up at a maximum value in the middle of the tubes.

  5. (5)

    The nanoparticles concentration C has an opposite behavior compared to the temperature behavior.