Abstract
We discuss a wide class of time inhomogeneous quantum evolution which is represented by two-parameter family of completely positive trace-preserving maps. These dynamical maps are constructed as infinite series of jump processes. It is shown that such dynamical maps satisfy time inhomogeneous memory kernel master equation which provides a generalization of the master equation involving the standard convolution. Time-local (time convolution-less) approach is discussed as well. Finally, the comparative analysis of traditional time homogeneous versus time inhomogeneous scenario is provided.
Similar content being viewed by others
Introduction
The dynamics of an open quantum system1,2 is usually represented by the dynamical map \(\{\Lambda _{t,t_0}\}_{t \ge t_0}\), i.e. a family of completely positive trace-preserving maps \(\Lambda _{t,t_0} : {\mathcal {B}}({\mathcal {H}}) \rightarrow {\mathcal {B}}({\mathcal {H}})\)3,4 (\({\mathcal {B}}({\mathcal {H}})\) stands for the vector space of bounded linear operators acting on the system’s Hilbert space \({\mathcal {H}}\)). In this paper we consider only finite dimensional scenario and hence \({\mathcal {B}}({\mathcal {H}})\) contains all linear operators. The map \(\Lambda _{t,t_0}\) transforms any initial system’s state represented by a density operator \(\rho _{0}\) at an initial time \(t_0\) into a state at the current time t, i.e. \(\rho _t = \Lambda _{t,t_0}(\rho _{0})\). Dynamical maps \(\{\Lambda _{t,t_0}\}_{t \ge t_0}\) provide the powerful generalization of the standard Schrödinger unitary evolution \(U_{t,t_0} \rho _{0} U_{t,t_0}^\dagger\), where \(U_{t,t_0}\) is a family of unitary operators acting on \({\mathcal {H}}\). A dynamical map is usually realized as a reduced evolution1
where \({\mathbb {U}}_{t,t_0}\) is a unitary operator acting on \({\mathcal {H}} \otimes {\mathcal {H}}_E\), \(\rho _E\) is a fixed state of the environment (living in \({\mathcal {H}}_E\)), and \(\textrm{Tr}_E\) denotes a partial trace (over the environmental degrees of freedom). The unitary \({\mathbb {U}}_{t,t_0}\) is governed by the total (in general time-dependent) ‘system + environment’ Hamiltonian \({\mathbb {H}}_t\). Now, if \({\mathbb {H}}_t={\mathbb {H}}\) does not depend on time the reduced evolution (1.1) is time homogeneous (or translationally invariant), i.e. \(\Lambda _{t,t_0} = \Lambda _{t-t_0}\) (or equivalently \(\Lambda _{t+\tau ,t_0+\tau } = \Lambda _{t,t_0}\) for any \(\tau\)). In this case one usually fixes \(t_0=0\) and simply considers one-parameter family of maps \(\{\Lambda _t\}_{t \ge 0}\). Such scenario is usually considered by majority of authors. The most prominent example of time homogeneous dynamical maps is the celebrated Markovian semigroup \(\Lambda _{t} = e^{{\mathcal {L}} t}\), where \({\mathcal {L}}\) denotes the Gorini–Kossakowski–Lindblad–Sudarshan (GKLS) generator5,6 (cf. also the detailed exposition in7 and8 for a brief history)
with the (effective) system’s Hamiltonian H, noise operators \(L_k\), and non-negative transition rates \(\gamma _k\). It is well known, however, that semigroup evolution usually requires a series of additional assumptions and approximations like e.g. weak system-environment interaction and separation of natural time scales of the system and environment. Departure from a semigroup scenario calls for more refined approach which attracts a lot of attention in recent years and is intimately connected with quantum non-Markovian memory effects (cf. recent reviews9,10,11,12,13,14,15,16,17). To go beyond dynamical semigroup keeping translational invariance one replaces time independent GKLS generator \({\mathcal {L}}\) by a memory kernel \(\{{\mathcal {K}}_t\}_{t\ge 0}\) and considers the following dynamical equation
where \(A \circ B\) denotes composition of two maps. Equation (1.3) is often referred as Nakajima–Zwanzig master equation18,19. The very structure of the convolution \({\mathcal {K}}_t *\Lambda _t\) does guarantee translational invariance. However, the property of complete positivity of \(\Lambda _t\) is notoriously difficult as already observed in20,21,22. Time non-local master equation (1.3) were intensively studied by several authors23,24,25,26,27,28,29,30,31,32,33,35. Since the master equation (1.3) involving the convolution is technically quite involved one usually tries to describe the dynamics in terms of convolution-less time-local approach involving a time dependent generator \(\{{\mathcal {L}}_t\}_{t \ge 0}\) (cf. the recent comparative analysis36). Time-local generator \({\mathcal {L}}_t\) plays a key role in characterizing the property of CP-divisibility which is essential in the analysis of Markovianity. Note, however, that the corresponding propagator \(\Lambda _{t,s} = \Lambda _t \circ \Lambda _s^{-1}\) is no longer time homogeneous unless \({\mathcal {L}}_t\) is time independent.
In this paper we go beyond time homogeneous case and consider the following generalization of (1.3)
which reduces to (1.3) if \({\mathcal {K}}_{t,\tau } = {\mathcal {K}}_{t-\tau }\). Equation (1.4) may be, therefore, considered as a time inhomogeneous Nakajima-Zwanzig master equation. Such description is essential whenever the ‘system + environment’ Hamiltonian \({\mathbb {H}}_t\) does depend on time. Note, that formally if \({\mathcal {K}}_{t,\tau } = {\mathcal {L}}_t \delta (t-\tau )\), then (1.4) reduces to time-local but inhomogeneous master equation
and the corresponding solution \(\Lambda _{t,t_0}\) is CPTP for all t and \(t_0\) with \(t>t_0\) if and only if \({\mathcal {L}}_t\) is of GKLS form for all \(t \in {\mathbb {R}}\)1,2,7. This is just inhomogeneous generalization of semigroup evolution and it is often called an inhomogeneous semigroup7. Note, that contrary to the homogeneous scenario where the time-local generator \({\mathcal {L}}_t = [\partial _t \Lambda _t] \circ \Lambda _t^{-1}\) is defined only for \(t \ge 0\) the time dependent generator \({\mathcal {L}}_t\) in (1.5) is defined now for all \(t\in {\mathbb {R}}\).
In this paper we propose a particular representation of dynamical maps \(\{\Lambda _{t,t_0}\}_{t\ge t_0}\) which by construction satisfy (1.4). Hence, it may be also considered as a particular construction of a legitimate class of memory kernels \({\mathcal {K}}_{t,\tau }\) giving rise to CPTP dynamical maps. Clearly, it is not the most general construction. However, the proposed representation possesses a natural physical interpretation in terms of quantum jumps. Time-local (time convolution-less) approach is discussed as well. It turns out that a time dependent generator also depends upon the initial time \(t_0\), i.e. one has a two-parameter family of generators \(\{{\mathcal {L}}_{t,t_0}\}_{t\ge t_0}\). Finally, the comparative analysis of traditional time homogeneous versus time inhomogeneous scenario is provided.
Time homogeneous evolution
Markovian semigroup
Consider a Markovian semigroup governed by the time independent master equation
where \({\mathcal {L}}\) stands for the GKLS generator (1.2), and \(t_0\) is an arbitrary initial time. It is clear that since \({\mathcal {L}}\) does not depend on time the dynamical map depends upon the difference \(t-t_0\), i.e. the solution of (2.1) defines one-parameter semigroup \(\Lambda _{t,t_0} = \Lambda _{t-t_0}= e^{(t-t_0){\mathcal {L}}}\). Usually, one assumes \(t_0=0\) and simply writes \(\Lambda _t\). Observe, that any GKLS generator (1.2) can be represented as follows
where \(\Phi , {\mathcal {Z}} : {\mathcal {B}}({\mathcal {H}}) \rightarrow {\mathcal {B}}({\mathcal {H}})\) are linear maps defined by
with \(C = iH + \frac{1}{2} \sum _k L_k^\dagger L_k\).
Proposition 1
The solution of Eq. (2.1) can be represented via the following series
where \(\Lambda ^{(0)}_t = e^{- {\mathcal {Z}} t}\).
Proof
let us introduce a perturbation parameter \(\lambda\) and a one-parameter family of generators
such that \({\mathcal {L}} = {\mathcal {L}}^{(\lambda =1)}\). We find a solution to
as a perturbation series
Inserting the series (2.7) into (2.6) one finds the following infinite hierarchy of equations
with initial conditions
It is clear that \(\Lambda ^{(0)}_t = e^{- {\mathcal {Z}}t}\), and
Finally, fixing \(\lambda =1\) the series (2.7) reduces to (2.4). \(\square\)
Note, that (2.4) is indeed time homogeneous. One finds
and
does depend upon ‘\(t-t_0\)’. A series (2.4) is an alternative representation for the conventional exponential representation
Note, that contrary to (2.13) each term in (2.4) is completely positive and has a clear physical interpretation: an \(\ell\)th term reads
and it can be interpreted as follows: there are \(\ell\) quantum jumps up to time ‘t’ at \(\{t_1 \le t_2 \le \ldots \le t_\ell \}\) represented by a completely positive map \(\Phi\). Between jumps the system evolves according to (unperturbed) completely positive maps \(\Lambda ^{(0)}_{t_2-t_1},\Lambda ^{(0)}_{t_3-t_2}, \ldots , \Lambda ^{(0)}_{t_\ell -t_{\ell -1}}\). The series (2.4) represents all possible scenario of \(\ell\) jumps for \(\ell =0,1,2,\ldots\). By construction, the resulting completely positive map \(\Lambda _t\) is also trace-preserving. One often calls (2.4) a quantum jump representation of a dynamical map37,37,39. Note, however, that truncating (2.4) at any finite \(\ell\) violates trace-preservation since processes with more than \(\ell\) jumps are not included. The standard exponential representation (2.13) does not have any clear interpretation. Each separate term \(t^k {\mathcal {L}}^k\) does annihilate the trace but is not completely positive. Only the infinite sum of such terms gives rise to completely positive (and trace-preserving) map.
Corollary 1
Introducing two completely positive maps \(Q_t := \Phi \circ \Lambda ^{(0)}_{t}\) and \(\,{\mathcal {P}}_t := \Lambda ^{(0)}_{t} \circ \Phi\) a series (2.4) can be rewritten as follows
To summarise: the Markovian semigroup represented in (2.4) is constructed out of the unperturbed completely positive and trace non-increasing map \(\Lambda ^{(0)}_t= e^{- {\mathcal {Z}} t}\) and the jump operator represented by a completely positive map \(\Phi\). These two objects are constrained to satisfy \(\textrm{Tr}{\mathcal {L}}(\rho ) = 0\), where \({\mathcal {L}} = \Phi - {\mathcal {Z}}\) defines a GKLS generator.
Beyond a semigroup
How to generalize (2.4) beyond a semigroup such that time homogeneity is preserved? Suppose that \(\Lambda ^{(0)}_t\) is an arbitrary completely positive and trace non-increasing map satisfying \(\Lambda ^{(0)}_{t=0} = \textrm{id}\). Let \(\{{\mathcal {Z}}_t\}_{t\ge 0}\) be a family of maps such that
that is, \({\mathcal {Z}}_t\) is a time non-nonlocal generator of \(\Lambda ^{(0)}_t\). Note, that \(\Lambda ^{(0)}_t\) defines a semigroup if and only if \({\mathcal {Z}}_t = \delta (t) {\mathcal {Z}}\). Consider a family of jump operators represented by completely positive maps \(\{\Phi _t\}_{t \ge 0}\). Define now the following generalization of (2.4)
that is, one replaces \(\Phi \circ \Lambda ^{(0)}_t\) by the convolution \(\Phi _t *\Lambda ^{(0)}_t\). By construction (2.17) represents a completely positive map being an infinite sum of completely positive maps
Also a similar quantum jump interpretation still remains true. One finds
Between jumps the system evolves according to (unperturbed) completely positive maps \(\Lambda ^{(0)}_{t_2-t_1},\Lambda ^{(0)}_{t_3-t_2}, \ldots , \Lambda ^{(0)}_{t_\ell -t_{\ell -1}}\) which are no longer semigroups.
Proposition 2
The map represented by (2.17) satisfies the following memory kernel master equation
where
The map \(\Lambda _t\) is trace-preserving if and only if \({\mathcal {K}}_t\) is trace annihilating.
Proof
the proof goes the same lines as that of Proposition 1. Introducing
and inserting (2.7) into
one obtains the following infinite hierarchy of equations
with initial conditions (2.9). We show that \(\Lambda ^{(\ell )}_{t} = \Lambda ^{(0)}_t *\Lambda ^{(\ell -1)}_{t}\) is a solution to (2.24) which immediately implies (2.18). Indeed, one has
and hence using \(\partial _t \Lambda ^{(0)}_t = - {\mathcal {Z}}_t *\Lambda ^{(0)}_t\), one obtains
which proves the claim. \(\square\)
Remark 1
Usually on solves the time homogeneous differential equations using the technique of Laplace transform. We provide the alternative proof of Proposition 2 in the Supplementary Information. Here, we provided the proof which can be easily generalized to inhomogeneous case where the Laplace transform technique can not be directly applied.
Remark 2
It is clear that if \(\Lambda ^{(0)}_t = e^{- {\mathcal {Z}}t}\) is a semigroup, i.e. \({\mathcal {Z}}_t = \delta (t) {\mathcal {Z}}\), then \(\Phi _t = \delta (t) \Phi\), and hence
Corollary 2
Introducing two completely positive maps \(Q_t := \Phi _t *\Lambda ^{(0)}_{t}\) and \(\,{\mathcal {P}}_t := \Lambda ^{(0)}_{t} *\Phi _t\) a series (2.17) can be rewritten as follows
or, equivalently,
that is, one has exactly the same representation as in the case of semigroup (2.15). The only difference is the definition of \(Q_t\) and \({\mathcal {P}}_t\) in terms of \(\Phi _t\) and \(\Lambda ^{(0)}_{t}\). Note, however, that if \(\Phi _t = \delta (t)\Phi\), then \(\Phi _t *\Lambda ^{(0)}_{t} = \Phi \circ \Lambda ^{(0)}_{t}\), i.e. one recovers the same relation as in Corollary 1.
Remark 3
It should be stressed that even when \(\Phi _t\) is not completely positive, but \(Q_t = \Phi _t *\Lambda ^{(0)}_{t}\) is completely positive, then (2.28) is completely positive. Similarly, when \(\,{\mathcal {P}}_t := \Lambda ^{(0)}_{t} *\Phi _t\) is completely positive, then (2.29) is completely positive. Hence, complete positivity of \(\Phi _t\) is sufficient but not necessary for complete positivity of the dynamical map \(\Lambda _t\). Note, however, if \(\Phi _t\) is not completely positive the intuitive interpretation of the series (2.17) in terms of quantum jumps is no longer valid.
Time inhomogeneous evolution
Time inhomogeneous semigroup
Consider now the dynamical map \(\{\Lambda _{t,t_0}\}_{t\ge t_0}\) governed by the time dependent master equation
where \({\mathcal {L}}_t\) stands for the time dependent GKLS generator, and \(t_0\) is an arbitrary initial time. The corresponding solution has the well known structure
where \({\mathcal {T}}\) stands for chronological time ordering. The two-parameter family of maps \(\{\Lambda _{t,t_0}\}_{t \ge t_0}\) satisfies the following composition law
for any triple \(\{t_1, t_2, t_3\}\). Such evolution is evidently CP-divisible. This very property is a generalization of the standard (homogeneous) semigroup property
and hence one often calls such maps an inhomogeneous semigroup.
Let us represent the time dependent generator as follows
where now
with \(C(t) = iH(t) + \frac{1}{2} \sum _k \gamma _k(t)L_k^\dagger (t) L_k(t)\). To find the corresponding jump representation of \(\Lambda _{t,t_0}\) let us introduce the following (inhomogeneous) generalization of the convolution.
Definition 1
For any two families of maps \(A_{t,t_0}\) and \(B_{t,t_0}\)
Note, that when \(A_{t,t_0}=A_{t-t_0}\) and \(B_{t,t_0}=B_{t-t_0}\), then
Proposition 3
The convolution (3.7) is associative
for any three families \(A_{t,t_0},\, B_{t,t_0}\) and \(C_{t,t_0}\).
See Supplementary Information for the proof.
Proposition 4
The solution to (3.1) can be represented via the following series
where \(\Lambda ^{(0)}_{t,t_0} = {\mathcal {T}} \exp \left( - \int _{t_0}^t {\mathcal {Z}}_\tau d \tau \right)\).
Proof
the proof is a generalization of the proof of Proposition 1. Consider the family of generators
We find a solution to
as a perturbation series
Inserting the series (3.13) into (3.12) one finds the following hierarchy of dynamical equations:
with initial conditions
Clearly, the above hierarchy provides a generalization of (2.8) for the inhomogeneous scenario. Now,
defines an inhomogeneous semigroup which is completely positive (but not trace-preserving). As before it is sufficient to show that
solves (3.14). One finds
Using \(\Lambda ^{(0)}_{t,t} = \textrm{id}\), and \(\partial _t\Lambda ^{(0)}_{t,t_0} = - {\mathcal {Z}}_t \circ \Lambda ^{(0)}_{t,t_0}\), one gets
and finally, observing that
one completes the proof. \(\square\)
For an alternative proof which does not use properties of the convolution ‘\(\circledast\)’ cf. Supplementary Information.
Beyond an inhomogeneous semigroup
Suppose now that for any initial time \(\Lambda ^{(0)}_{t,t_0}\) is an arbitrary completely positive and trace non-increasing map satisfying \(\Lambda ^{(0)}_{t_0,t_0} = \textrm{id}\). Let \(\{{\mathcal {Z}}_{t,t_0}\}_{t\ge t_0}\) be a family of maps such that
that is \(\{{\mathcal {Z}}_{t,t_0}\}_{t\ge t_0}\) is a inhomogeneous generalization of \(\{{\mathcal {Z}}_t\}_{t\ge 0}\). Now, \({\mathcal {Z}}_{t,t_0}\) does not only depends upon the current time ‘t’ but also upon the initial time \(t_0\). Define the following generalization of (3.10)
where \(\{\Phi _{t,t_0}\}_{t\ge t_0}\) is a family of completely positive maps which reduces to \(\{\Phi _t\}_{t\ge 0}\) in the time homogeneous case. Hence, one replaces \(\Phi _t \circ \Lambda ^{(0)}_{t,t_0}\) by the convolution \(\Phi _{t,t_0} \circledast \Lambda ^{(0)}_{t,t_0}\). By construction Eq. (3.22) represents a completely positive map being an infinite sum of completely positive maps
Clearly, quantum jump interpretation still remains true.
Proposition 5
The map represented by (3.22) satisfies the following memory kernel master equation
where
The map \(\Lambda _{t,t_0}\) is trace-preserving if and only if \({\mathcal {K}}_{t,t_0}\) is trace annihilating.
Proof
the proof goes the same lines as that of Propositions 2 and 4. One easily finds the following hierarchy of equations for maps \(\Lambda ^{(\ell )}_{t,t_0}\) defining the series (3.13):
with initial conditions (3.15). Clearly, the above hierarchy provides a generalization of (2.24) for the inhomogeneous scenario. It is enough to prove that
One has
Using \(\Lambda ^{(0)}_{t,t} = \textrm{id}\), and \(\partial _t\Lambda ^{(0)}_{t,t_0} = - {\mathcal {Z}}_{t,t_0} \circledast \Lambda ^{(0)}_{t,t_0}\), one gets
and hence
which ends the proof. \(\square\)
Corollary 3
Introducing two completely positive maps \(Q_{t,t_0} := \Phi _{t,t_0} \circledast \Lambda ^{(0)}_{t,t_0}\) and \(\,{\mathcal {P}}_{t,t_0} := \Lambda ^{(0)}_{{t,t_0}} \circledast \Phi _{t,t_0}\) a series (2.17) can be rewritten as follows
or, equivalently,
They reduce to (2.28) and (2.29) in the time homogeneous case.
Table 1 summarizes the construction of time homogeneous versus time inhomogeneous dynamical maps.
Time local approach
Very often describing the evolution of an open system one prefers to use a time-local (or so-called convolutionless (TCL)) approach1. Formally, in the time homogeneous case given a dynamical map \(\{\Lambda _t\}_{t\ge 0}\) one defines the corresponding time-local generator \({\mathcal {L}}_t := [\partial _t \Lambda _t] \circ \Lambda _t^{-1}\) (assuming that \(\Lambda _t\) is invertible). This way the map \(\Lambda _t\) satisfies
This procedure might be a bit confusing since (4.1) coincides with (3.1) for the inhomogeneous map \(\Lambda _{t,t_0}\). To clarify this point let us introduce again an initial time and consider \(\Lambda _{t,t_0} = \Lambda _{t-t_0}\). Now, the time-local generator reads
that is, the generator does depend upon the initial time40. It implies that the corresponding propagators
also does depend upon \(t_0\). Clearly, fixing \(t_0=0\) this fact is completely hidden. The dependence upon \(t_0\) drops out only in the semigroup case when \({\mathcal {L}}_{t-t_0} = {\mathcal {L}}\).
Similar analysis may be applied to inhomogeneous scenario as well. Now, instead of convolution (3.21) one may define a time-local generator
such that \(\Lambda _{t,t_0}\) satisfies the following inhomogeneous TCL master equation
Again, the corresponding propagator
also does depend upon \(t_0\). Hence, the local composition law
holds only if the above propagators are defined w.r.t. the same initial time. Otherwise, composing the propagators does not have any sense. Equation (4.5) reduces to (3.1) only if \({\mathcal {L}}_{t,t_0}\) does not depend upon \(t_0\). In this case one recovers an inhomogeneous semigroup and \({\mathcal {L}}_{t,t_0} = {\mathcal {L}}_{t}\).
Conclusions
We have constructed a family of time inhomogeneous dynamical maps \(\{\Lambda _{t,t_0}\}_{t\ge 0}\) represented by the following infinite series
where each single map \(\Lambda ^{(\ell )}_{t,t_0}\) is completely positive. Moreover, the construction does guarantee that \(\Lambda _{t,t_0}\) is trace-preserving. Each map \(\Lambda ^{(\ell )}_{t,t_0}\) represents a process with \(\ell\) quantum jumps occurring in the interval \([t_0,t]\). The ‘free’ evolution (no jumps) corresponds to \(\Lambda ^{(0)}_{t,t_0}\). Quantum jumps are represented by a family of completely positive maps \(\{\Phi _{t,t_0}\}_{t\ge t_0}\) such that \(\Lambda ^{(\ell )}_{t,t_0}\) is represented as in the Table 1.
In the time-homogeneous case the above representation simplifies to
with a similar interpretation. The dynamical map \(\Lambda _{t,t_0}\) satisfies the corresponding Nakajima-Zwanzig memory kernel master equation or equivalently time-local (TCL) master equation displayed in the Table 2.
Interestingly, apart from Nakajima-Zwanzing memory kernel master equation the map \(\Lambda _{t,t_0}\) satisfies the following dynamical equation
where the new kernel \({\mathbb {K}}_{t,t_0}\) is defined by
that is, it is constructed in terms of the ‘free’ evolution represented by \(\Lambda _{t,t_0}^{(0)}\) and the jump operators \(\Phi _{t,t_0}\) (the details of the derivation are presented in the Supplementary Information).
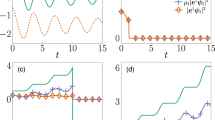
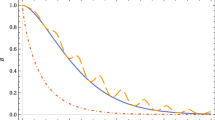
This is very general class of legitimate quantum evolutions and corresponding dynamical equations. It would be interesting to apply the above scheme to discuss time inhomogeneous semi-Markov processes28,29,33,41 and collision models (cf.42 for the recent review).
Data availibility
All data generated or analysed during this study are included in this published article and its supplementary information file.
References
Breuer, H.-P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford University Press, 2007).
Rivas, A. & Huelga, S. F. Open Quantum Systems. An Introduction (Springer, 2011).
Paulsen, V. Completely Bounded Maps and Operator Algebras (Cambridge University Press, 2003).
Størmer, E. Positive Linear Maps of Operator Algebras, Springer Monographs in Mathematics (Springer, 2013).
Gorini, V., Kossakowski, A. & Sudarshan, E. C. G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 17, 821 (1976).
Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119 (1976).
Alicki, R. & Lendi, K. Quantum Dynamical Semigroups and Applications (Springer, 1987).
Chruściński, D. & Pascazio, S. A Brief History of the GKLS Equation. Open Sys. Inf. Dyn. 24, 1740001 (2017).
Rivas, Á., Huelga, S. F. & Plenio, M. B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 77, 094001 (2014).
Breuer, H.-P., Laine, E.-M., Piilo, J. & Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 88, 021002 (2016).
de Vega, I. & Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 89, 015001 (2017).
Li, L., Hall, M. J. W. & Wiseman, H. M. Concepts of quantum non-Markovianity: A hierarchy. Phys. Rep. 759, 1 (2018).
Reimer, V., Wegewijs, M. R., Nestmann, K. & Pletyukhov, M. Five approaches to exact open-system dynamics: Complete positivity, divisibility, and time-dependent observables. J. Chem. Phys. 151, 044101 (2019).
Lidar, D.A. Lecture notes on the theory of open quantum systems. arXiv:1902.00967.
Chruściński, D. Dynamical maps beyond Markovian regime. Phys. Rep. 992, 1 (2022).
Li, C. F., Guo, G. C. & Piilo, J. Non-Markovian quantum dynamics: What does it mean?. EPL 127, 50001 (2019).
Li, C. F., Guo, G. C. & Piilo, J. Non-Markovian quantum dynamics: What is it good for?. EPL 128, 30001 (2019).
Nakajima, S. On quantum theory of transport phenomena. Prog. Theor. Phys. 20, 948 (1958).
Zwanzig, R. Ensemble method in the theory of irreversibility. J. Chem. Phys. 33, 1338 (1960).
Barnet, S. M. & Stenholm, S. Hazards of reservoir memory. Phys. Rev. A 64, 033808 (2001).
Shabani, A. & Lidar, D. A. Completely positive post-Markovian master equation via a measurement approach. Phys. Rev. A. 71, 020101 (2005).
Campbell, S. et al. Critical assessment of two-qubit post-Markovian master equations. Phys. Rev. A 85, 032120 (2012).
Budini, A. Stochastic representation of a class of non-Markovian completely positive evolutions. Phys. Rev. A. 69, 042107 (2004).
Budini, A. & Grigolini, P. Non-Markovian non-stationary completely positive open quantum system dynamics. Phys. Rev. A 80, 022103 (2009).
Wilkie, J. & Wong, Y. M. Sufficient conditions for positivity of non-Markovian master equations with Hermitian generators. J. Phys. A Math. Gen. 42, 015006 (2009).
Maniscalco, S. & Petruccione, F. Non-Markovian dynamics of a qubit. Phys. Rev. A 73, 012111 (2006).
Kossakowski, A. & Rebolledo, R. On the structure of generators for non-Markovian master equations. Open Syst. Inf. Dyn. 16, 259 (2008).
Breuer, H.-P. & Vacchini, B. Quantum semi-Markov processes. Phys. Rev. Lett. 101, 140402 (2008).
Breuer, H.-P. & Vacchini, B. Structure of completely positive quantum master equations with memory kernel. Phys. Rev. E 79, 041147 (2009).
Vacchini, B. Non-Markovian master equations from piecewise dynamics. Phys. Rev. A. 87, 030101 (2013).
Chruściński, D. & Kossakowski, A. From Markovian semigroup to non-Markovian quantum evolution. EPL 97, 20005 (2012).
Chruściński, D. & Kossakowski, A. Sufficient conditions for a memory-kernel master equation. Phys. Rev. A. 94, 020103(R) (2016).
Chruściński, D. & Kossakowski, A. Generalized semi-Markov quantum evolution. Phys. Rev. A 95, 042131 (2017).
Vacchini, B. Generalized master equations leading to completely positive dynamics. Phys. Rev. Lett. 117, 230401 (2016).
Lorenzo, S., Ciccarello, F. & Palma, G. M. Class of exact memory-kernel master equations. Phys. Rev. A. 93, 052111 (2016).
Megier, N., Smirne, A. & Vacchini, B. The interplay between local and non-local master equations: Exact and approximated dynamics. New J. Phys. 22, 083011 (2020).
Gardiner, C. W. & Zoller, P. Quantum Noice (Springer, 1999).
Plenio, M. B. & Knight, P. L. The quantum-jump approach to dissipative dynamics in quantum optics. Rev. Mod. Phys. 70, 101 (1998).
Carmichael, H. J. An Open Systems Approach to Quantum Optics (Springer, 1993).
Chruściński, D. & Kossakowski, A. Non-Markovian quantum dynamics: Local versus nonlocal. Phys. Rev. Lett. 104, 070406 (2010).
Vacchini, B. Quantum renewal processes. Sci. Rep. 10, 5592 (2020).
Ciccarello, F., Lorenzo, S., Giovannetti, V. & Palma, G. M. Quantum collision models: Open system dynamics from repeated interactions. Phys. Rep. 954, 1 (2022).
Acknowledgements
The work was supported by the Polish National Science Centre project No. 2018/30/A/ST2/00837.
Author information
Authors and Affiliations
Contributions
D.C. proposed the main idea, peformed all technical analysis, and constructed a manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chruściński, D. Time inhomogeneous quantum dynamical maps. Sci Rep 12, 21223 (2022). https://doi.org/10.1038/s41598-022-25694-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-25694-1
This article is cited by
-
Quantum error channels in high energetic photonic systems
Scientific Reports (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.