Introduction

Magnetocaloric effect (MCE) is one of the most promising cooling technology for commercial and cryogenic applications1. Magnetic cooling based on MCE is considered a highly efficient and environmentally friendly alternative to the conventional gas compression method2,3,4. Although much research effort is focused on searching high efficient refrigerants near room temperature (for air conditioning or refrigerators)5,6,7,8,9,10, the ultra-low temperature range11,12,13,14,15,16 is no less important as a cost-effective alternative to 3He dilution refrigerators. The later application will grow in importance as a result of the development of quantum computers which require cryogenic conditions. However, most MCE refrigerants require high magnetic field changes (on the order of µ0ΔH ≈ 5–7 T), which is far above the capabilities of modern permanent magnets and therefore limits the application of MCE.

Conventional MCE is a thermodynamic process in which the magnetic material alters its temperature under the change of an external magnetic field17,18,19,20,21. However, there is another approach for magnetic cooling that involves the anisotropic magnetocaloric materials, namely the rotating magnetocaloric effect (RMCE)22,23,24,25. In the conventional MCE, the refrigerant is moving in and out of a magnetic field, or the external magnetic field is applied and removed. In the case of RMCE, aligned single crystals with significant magnetic anisotropy are rotated in a constant magnetic field17,26,27,28,29,30,31,32. A practical reason for this approach lies in the fact that mechanical rotations of the sample are much easier to perform and more efficient because of the operation at higher frequencies than field sweeps, thus minimizing the number of irreversible heat flows30,33,34,35. Additional energy savings for RMCE can be reached using permanent magnets.

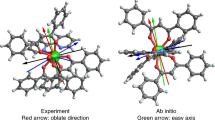
In this work, we present the anisotropic MCE and RMCE studies on two SMM ZnII–LnIII–ZnII trinuclear complexes [LnIII(ZnIIL)2]CF3SO3, where Ln = Tb (Tb-SMM), Dy (Dy-SMM) and L denotes a tripodal hexadentate Schiff-base ligand. In our previous works 36,37, it was shown that both compounds are paramagnetic (no long-range magnetic order down to 2.0 K), reveal SMM behavior and have strong magnetic anisotropy with an easy axis along the crystallographic c axis which passes through the Zn–Ln–Zn array. The large uniaxial anisotropy makes the studied molecular magnets prospective candidates for RMCE. Single crystal magnetic measurements were performed along the easy axis (c∥H) and within the hard plane (ab∥H) to obtain the magnetic entropy change for conventional and rotating magnetocaloric effects. Both compounds reveal large RMCE at 2.0 K in moderate fields, which are easily accessible with permanent magnets.

Results

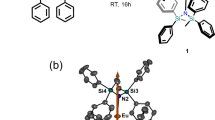
Both compounds crystallizes in the trigonal crystal system with space group R32, with the unit cell parameters of a = 11.8682(4) Å, c = 38.4392(16) Å, V = 4688.9(3) Å3 for Tb-SMM and a = 11.9081(4) Å, c = 38.2125(18) Å, V = 4692.7(3) Å3 for Dy-SMM, respectively36,37. The structure consists of two separated ions: a cationic trinuclear cluster [LnIII(ZnIIL)2]+ with rare earth LnIII = TbIII/DyIII as a central ion and a non-magnetic CF3SO3− anion (Fig. 1b). A crystallographic three-fold axis passes through the Zn–Tb–Zn array and is parallel to the crystallographic c axis. Three two-fold axes are located on LnIII = TbIII/DyIII central ion and are perpendicular to the C3 axis, and hence the molecule belongs to the D3 point group symmetry. The coordination sphere around the LnIII = TbIII/DyIII ion is fully occupied by 12 oxygen atoms, with the short-bonded phenoxo oxygen donors (2.3651(19) Å for Tb-SMM and 2.3437(19) Å for Dy-SMM) at above and below positions and long-attached methoxy oxygen donors (3.0465(15) Å and 3.076(2) Å) located at the equatorial positions. Obtained single crystals were flat and formed the hexagonal-like shape with the crystallographic axis c being perpendicular to the surface of the crystal and ab crystallographic plane lying in the plane of the surface (Fig. 1a).

Figure 1
figure 1

(a) The orientation of the monocrystal with the real space directions. (b) Crystal structures of the LnIII(ZnIIL)2 unit with LnIII = TbIII (Tb-SMM), DyIII (Dy-SMM) and the CF3SO3− anion. The view is along a axis, and hydrogen atoms are omitted for clarity. The CF3SO3− anion is disordered in two positions related by C2 axis, each with an occupancy of 0.5.

Full size image

Single crystal magnetometry measurements of Tb-SMM and Dy-SMM were performed within the ab plane (ab∥H) and along the c axis (c∥H). Figure 2 shows the isothermal magnetization M(H) of Tb-SMM and Dy-SMM at T = 2.0 K. In both samples, the c||H is the easy magnetization direction, with saturation magnetization MS ≈ 8.9 µB mol−1. The crystal field calculation for Tb-SMM36 revealed that in a non-zero magnetic field the lowest lying states of Tb3+ ions display maximal values of \(\left\langle {J_{z} } \right\rangle\) =  ± 6. Taking into account gTb = 3/2, the expected value of saturation reaches 9 µB mol−1, which is close to the measured Ms. In the case of Dy-SMM the crystal field analysis37 revealed that the ground state of the Dy3+ ion is degenerated and corresponds to the |± 13/2〉 substates, which points to ≈ 8.7 µB mol−1 for gDy = 4/3. The ab crystallographic plane is the hard magnetization plane with maximum values of 0.5 µB mol−1 (≈ 6% of MS) for Tb-SMM at µ0H = 4 T and 3.8 µB mol−1 (≈ 43% of MS) for Dy-SMM at µ0H = 7 T.

Figure 2
figure 2

The isothermal magnetization of Tb-SMM and Dy-SMM at T = 2.0 K measured for ab∥H and c∥H orientations in the applied field range µ0H = 0–7 T, except for Tb-SMM in ab∥H, for which the highest field was µ0H = 4 T (see “Materials and methods” section). Inset pictures present the orientation of the sample regarding the external field H.

Full size image

The dc magnetic susceptibility χ(T) was measured during the sample cooling from T = 300 K to T = 2.0 K in an applied magnetic field of µ0H = 0.1 T (Fig. 3). Figure 3 shows the collected data in the form of the χT product for both compounds in c∥H and ab∥H. The χT values for Tb-SMM and Dy-SMM reveal significant differences between the easy axis and the hard plane in the entire temperature range, which point to substantial magnetic anisotropy in both studied compounds (for detailed analysis of magnetic properties, see 36).

Figure 3
figure 3

The product of molar magnetic susceptibility and temperature χT for Tb-SMM and Dy-SMM measured in function of temperature from 300 to 2 K for c∥H and ab∥H orientations in the static magnetic field µ0H = 0.1 T.

Full size image

The MCE was evaluated using the indirect method for the isothermal magnetization measurements M(T, H) recorded in the temperature range of T = 2–80 K and magnetic field µ0H up to 7.0 T for ab∥H and c∥H orientations (up to 4.0 T for Tb in ab∥H orientation). The magnetic entropy change ΔS(T, H) was calculated using the Maxwell relationship:

$$\begin{array}{c}\Delta S\left(T,H\right)={\mu }_{0}\underset{0}{\overset{H}{\int }}{\left(\frac{\partial M\left(T,{H}_{1}\right)}{\partial T}\right)}_{{H}_{1}}d{H}_{1}.\end{array}$$
(1)

The − ΔS(T, H) temperature dependence for selected fields is shown in Fig. 4. A significant difference in MCE was observed between both orientations. The magnitude of MCE was larger for c∥H than for ab∥H for both compounds, and additionally, a peak of the -ΔS(T, H) appeared for magnetic field µ0H ≥ 3 T in the case of c∥H but was absent for ab∥H. For Tb-SMM, the maximum entropy change − ΔSmax was observed at T = 2.0 K reaching -ΔSmax = 4.21 J K−1 kg−1 for c∥H in µ0ΔH = 7 T and − ΔSmax = 1.23 J K−1 kg−1 for ab∥H in µ0ΔH = 4 T. In case of Dy-SMM the maximum of − ΔS was found in µ0ΔH = 7 T reaching − ΔSmax = 4.72 J K−1 kg−1 at T = 6.0 K for c∥H and − ΔSmax = 2.98 J K−1 kg−1 at T = 2.0 K for ab∥H.

Figure 4
figure 4

The temperature dependence of entropy change − ΔS(T, H) for various magnetic field changes for Tb-SMM and Dy-SMM estimated for the c∥H and ab∥H orientations. Solid lines are guides for the eyes.

Full size image

To study the RMCE, the magnetic entropy change related to the rotation of a single crystal was calculated as the difference − ΔSR = − (ΔSc∥H − ΔSab∥H), where ΔSc∥H and ΔSab∥H are the entropy changes for c∥H and ab∥H respectively. Figure 5 depicts − ΔSR temperature dependence for Tb-SMM and Dy-SMM. One can notice the presence of the peak that was also observed for the conventional MCE for c∥H, which for the RMCE entropy change is broader. Moreover, the position of this peak has moved towards higher temperatures. The shift was from T = 4.5 K to T = 7.0 K for µ0H = 4 T for Tb-SMM, and for Dy-SMM, from T = 5.5 K to T = 8.0 K for µ0H = 4 T, and T = 6.0 K to T = 16.0 K for µ0H = 7 T.

Figure 5
figure 5

The RMCE entropy change − ΔS(T, H) as a function of the temperature T ranging from 2 to 80 K for the selected magnetic fields µ0H for Tb-SMM and Dy-SMM. Solid lines are guides for the eyes.

Full size image

Figure 6 shows the RMCE entropy change as a function of the applied magnetic field for selected temperatures for Tb-SMM and Dy-SMM. The maximum RMCE entropy change − ΔSmax was obtained at T = 2.0 K for both compounds for relatively low magnetic fields. For Tb-SMM, − ΔSmax was found for µ0H = 1.3 T with − ΔSmax = 3.94 J K−1 kg−1, and for Dy-SMM for µ0H = 1.1 T with − ΔSmax = 3.3 J K−1 kg−1. One can notice that the peak of the − ΔS moves towards higher temperatures with an increasing magnetic field. Therefore, for low magnetic fields, the RMCE is greater at lower temperatures, whereas high fields are more advantageous at higher temperatures. For Tb-SMM, in µ0H = 4 T, − ΔSmax is found at T = 7 K, and for Dy-SMM in µ0H = 7 T at T = 14 K.

Figure 6
figure 6

The RMCE entropy change − ΔS(T, H) as a function of the magnetic field µ0H up to 7 T for the selected temperatures for Tb-SMM and Dy-SMM. Solid lines are guides for the eyes.

Full size image

The utility of material for magnetocaloric cooling applications can be evaluated using the proposed Temperature averaged Entropy Change (TEC) figure of merit 38,39,40,41:

$$\begin{array}{c}TEC\left(\Delta {T}_{\text{lift}}\right)=\frac{1}{\Delta {T}_{\text{lift}}}\underset{{T}_{\text{mid}}}{\mathrm{max}}\left\{{\int }_{{T}_{\text{mid}}-\frac{\Delta {T}_{\text{lift}}}{2}}^{{T}_{\text{mid}}+\frac{\Delta {T}_{\text{lift}}}{2}}\left|\Delta S\left(T,H\right)\right|dT\right\}.\end{array}$$
(2)

It is estimated for the specific temperature range ΔTlift = Thot − Tcold in which the refrigerating material can potentially work, where Thot and Tcold are temperatures of cold and hot reservoirs, respectively. The integral is maximized for the center of the average, Tmid, chosen by sweeping over the available ΔS(T, H) data. In our study, the temperature interval ΔTlift was set between 1 and 30 K with a fixed step of 1 K.

The dependence of TEC on ΔTlift in µ0H = 1 T, 4 T was depicted in Fig. 7 for Tb-SMM and Dy-SMM for conventional MCE in c∥H and ab∥H orientations and RMCE. As expected for ab∥H, the TEC was small compared to the easy axis geometry for both compounds regardless of the magnetic field value. In µ0H = 1 T, the TEC performances were almost identical in four cases: in c∥H orientation for Tb-SMM and Dy-SMM, RMCE for Tb-SMM, and slightly lower for RMCE for Dy-SMM (down to 85% of the corresponding TEC for the other three cases). The TEC values monotonically decreased with ΔTlift for both compounds and all orientations in the analyzed range. The situation is different in µ0H = 4 T, for which the TEC(ΔTlift) curves split. Although for Tb-SMM, the TEC for RMCE still amounts to approximately 90% of corresponding TEC for c∥H orientation, the same ratio was reduced to 70% for Dy-SMM. Additionally, the TEC values were relatively constant in the range ΔTlift = 1–6 K for c∥H and RMCE for both SMMs. For larger values of ΔTlift, TEC started to decrease linearly.

Figure 7
figure 7

The temperature averaged entropy change (TEC) in the function of temperature interval ΔTlift for conventional MCE and RMCE for Tb-SMM and Dy-SMM calculated for the applied magnetic field of µ0H = 1 T (a) and µ0H = 4 T (b).

Full size image

The temperature interval of ΔTlift = 5 K was selected to study the field dependence of TEC(5) for Tb-SMM and Dy-SMM. The results are presented in Fig. 8. For Tb-SMM in c∥H orientation, TEC initially increased with the magnetic field up to µ0H = 4 T and reached a plateau for higher fields. In µ0H = 1 T, TEC was equal to 2.46 J K−1 kg−1, and in µ0H = 4–7 T to 3.83 J K−1 kg−1. Similar behavior was observed for RMCE for the same compound, obtaining TEC = 2.42 J K−1 kg−1 in µ0H = 1 T and TEC = 3.55 J K−1 kg−1 in µ0H = 4 T. In hard geometry, a monotonic increase of TEC with the magnetic field was observed with TEC = 0.04, 0.48 J K−1 kg−1 in µ0H = 1, 4 T, respectively. For Dy-SMM in c∥H orientation, TEC increased in the whole magnetic field range reaching TEC = 2.38, 4.2, 4.68 J K−1 kg−1 in µ0H = 1, 4, 7 T, respectively. The corresponding TEC for RMCE increased with the magnetic field up to µ0H = 3 T, and then it started decreasing. The obtained values for RMCE were equal to TEC = 2.13, 2.91, 2.61 J K−1 kg−1 in µ0H = 1, 4, 7 T, respectively. As for Tb-SMM in hard geometry, the corresponding TEC for Dy-SMM showed a monotonic increase of TEC with magnetic field with TEC = 0.26, 1.66, 2.61 J K−1 kg−1 in µ0H = 1, 4, 7 T, respectively.

Figure 8
figure 8

The temperature averaged entropy change (TEC) in the function of applied magnetic field µ0H calculated for temperature interval ΔTlift = 5 K for conventional MCE and RMCE for Tb-SMM and Dy-SMM.

Full size image

Discussion

Although the obtained − ΔSmax for Tb-SMM and Dy-SMM are approximately ten times smaller than the recently reported values for magnetic coolers based on Gd ions with − ΔSmax = 30–50 J K−1 kg−1 in µ0H = 7 T 42,43,44, it should be noted that the RMCE reported in this study brings a few essential advantages. The magnetic fields at which the RMCE exhibits − ΔSmax (µ0H = 1.3 T (Tb-SMM), 1.1 T (Dy-SMM)) are easily accessible by the permanent magnets; therefore, the potential magnetic cooler based on Tb-SMM or Dy-SMM could operate without superconducting magnets. The RMCE-based refrigerator can also work at higher frequencies and thus with greater efficiency than the conventional MCE. Last but not least, the problem of low heat conductivity and dissipation of the released heat 21 may be overcome due to the flat geometry of the crystals used and thus a large surface-to-volume ratio. The RMCE properties for selected compounds are compared in Table 1. In high field conditions (µ0H = 5.0 T) and Tmax (the temperature at which − ΔS reaches maximum value), there are many examples of refrigerants revealing giant RMCE, which is much higher than those observed for Tb-SMM and Dy-SMM. However, from economical point of view, the most interesting conditions are low fields (µ0H = 1.0 T, easily accessible with permanent magnets) and T = 2.0 K (which can be easily reached by pumping liquid 4He). In these conditions (µ0H = 1.0 T and T = 2.0 K), both investigated compounds reveal high performance, comparable to other refrigerants with giant RMCE.

Table 1 Examples of rotating magnetocaloric properties of selected potential refrigerants.
Full size table

Recently reported materials for conventional MCE show the variation of TEC(5) in µ0ΔH = 1 T between 1 and 10 J K−1 kg−1 41,48,49,50,51,52,53; thus, the RMCE results reported for Tb-SMM and Dy-SMM fall in a moderate range with TEC(5) = 2.42 J K−1 kg−1 for the former and TEC(5) = 2.13 J K−1 kg−1 for the latter in the same magnetic field. The studies of the RMCE in HoNiGe3 single crystal 54 presented a much higher TEC(5) of approximately 12 J K−1 kg−1 in µ0ΔH = 5 T compared to the corresponding values of 3.55 J K−1 kg−1 in µ0H = 4 T for Tb-SMM, and 2.82 J K−1 kg−1 in µ0H = 5 T for Dy-SMM, but with significantly smaller entropy change in µ0ΔH = 1 T and higher temperatures for which the entropy change maximum was observed (between 5 and 15 K). Therefore, Tb-SMM and Dy-SMM are potentially more attractive candidates for ultra-low temperature cooling with permanent magnets.

The large difference between MCE for c∥H and ab∥H makes the RMCE nearly as efficient as the conventional MCEc∥H measured for c∥H, what is pictured by the RMCE/MCEc∥H ratio in Fig. 9. In the case of Tb-SMM, the RCME/MCEc∥H value does not drop below the level of 90% for all temperatures measured in the magnetic fields up to µ0H = 2 T. Moreover, the ratio increases monotonically with the temperature in the full range of measured fields. The relative efficiency of RMCE is lower for Dy-SMM, for which the ratio RCME/MCEc∥H was higher than 90% only for T = 2–10 K and magnetic fields up to about µ0H = 1 T. The difference in RCME/MCEc∥H between Tb-SMM and Dy-SMM is directly related to MCE within the hard plane (ab∥H), which is substantially weaker for Tb-SMM. Ideally, the RMCE should be the most efficient in a system for which the conventional MCE almost vanishes in one of the crystal orientations and is large for another orientation.

Figure 9
figure 9

The ratio RMCE/MCEc∥H between RMCE and conventional MCE measured for c∥H at T = 2–80 K for Tb-SMM in magnetic fields up to µ0H = 4 T and Dy-SMM in fields up to µ0H = 7 T. Solid lines are guides for the eyes.

Full size image

Figure 10 shows field dependence of temperature at which the − ΔSR reveals a peak (Tpeak). The peaks could be observed only under certain conditions: T = 4.5–7 K and µ0H = 2–4 T for Tb-SMM and T = 4.5–16 K and µ0H = 2–7 T for Dy-SMM. For both compounds, the Tpeak shifts to higher temperatures with increasing the magnetic field. Magnetic field splits the energy levels due to the Zeeman splitting. The higher the field, the greater the splitting. In higher fields, stronger thermal fluctuations are required to populate the shifted states. Therefore, the temperature of the Tpeak is increasing with increasing magnetic field. The solid lines in Fig. 10 represent the best linear fit to the obtained points giving a = 1.24(40) K/T, b = 1.5(1.2) K and a = 1.55(10) K/T, b = 1.51(46) K for Tb-SMM and Dy-SMM respectively.

Figure 10
figure 10

Field dependence of Tpeak for Tb-SMM and Dy-SMM. The solid lines are the best fits to the linear function.

Full size image

Conclusions

The single crystal MCE of DyIII and TbIII based magnetic clusters were investigated in easy direction c∥H and hard plane ab∥H. It was shown that the presence of large magnetic anisotropy can have a substantial impact on the magnetic entropy change in two perpendicular orientations. The MCE for c∥H is higher in magnitude than for ab∥H and has a maximum peak, which is not the case for ab∥H. Because of these properties, the detailed research of RMCE was done for both studied compounds.

Although Tb-SMM reveals lower values of conventional MCE than Dy-SMM, regardless of temperature and field conditions, the efficiency of RMCE is greater for Tb-SMM due to substantially higher magnetic anisotropy of the Tb compound. The maximum of the entropy change − ΔSmax for RMCE was found at T = 2.0 K with − ΔSmax = 3.94 J K−1 kg−1 in µ0H = 1.3 T for Tb-SMM and − ΔSmax = 3.3 J K−1 kg−1 in µ0H = 1.1 T for Dy-SMM.

The performance of RMCE evaluated from TEC (Tlift = 5 K) is comparable with conventional MCE in all measured magnetic fields for Tb-SMM and up to approximately µ0H = 1 T for Dy-SMM (the difference between TECs for RMCE and MCE was less than 10%). TECs obtained for Tb-SMM and Dy-SMM are almost the same up to µ0H = 1.5 T, but for higher magnetic fields, Dy-SMM outperforms Tb-SMM by 9% in µ0H = 4 T and 18% in µ0H = 7 T based on that figure of merit. However, TEC for RMCE indicates that the Tb-SMM single crystal is a better material for magnetocaloric cooling, with 12% higher TEC in µ0H = 1 T and 18% higher TEC in µ0H = 4 T than the corresponding TEC for Dy-SMM.

The relative efficiency of RMCE was calculated as the ratio RMCE/MCEc∥H between entropy changes. The best efficiency is obtained at low magnetic fields, reaching almost 100% at all temperatures studied for Tb-SMM and 95% at T = 2.0 K for Dy-SMM. The peak position of the entropy change for RMCE moves towards higher temperatures with increasing magnitude of the magnetic field. The mutual relation between peak position coordinates (temperature, magnetic field) may be described using a linear function.

Materials and methods

The single crystals of Tb-SMM36 and Dy-SMM37 were synthesized according to the literature procedures.

All the magnetic measurements were carried out with the MPMS XL magnetometer from Quantum Design. Single crystals of each compound were aligned in predetermined directions and mounted with Varnish GE adhesive. The plates with the single crystal were attached to a low-signal plastic straw to keep the specified orientation of the sample with respect to the magnetic field.

The studies were performed in two single crystal orientations: ab∥H and c∥H. The isothermal magnetization M(H) was collected at T = 2–80 K in the field range of µ0H = 0–7 T for Tb-SMM in the c∥H orientation and Dy-SMM for both geometries. The magnetic field range for Tb-SMM for ab∥H was reduced to µ0H = 0–4 T because the strong magnetic torque leads to breaking the sample in higher fields. The dc magnetic susceptibility χ(T) was measured during the cooling from T = 300 K to T = 2.0 K under µ0H = 0.1 T. The mass of single crystals was 6.51 mg for Tb-SMM and 1.87 mg for Dy-SMM. All measurements were corrected for diamagnetic contribution using Pascal’s constants55.