Introduction

Heat transfer is the transmission of energy induced by temperature variations and if two systems in contact have different temperatures, heat transfer occurs until thermal equilibrium is reached. The innovation of effective heat transfer liquids with elevated thermal conductivity and heat transfer coefficient is required to improve the efficiency of the heat transmission process and to reduce the cost and size of the relevant modules and devices. The suspension of tiny solid particulate in liquids is an effective method of increasing the thermal conductivity of liquids and thereby enhances the heat transference phenomenon. Using these kinds of liquids, several investigators explored the features of heat transferal1,2,3,4,5,6,7. On the other side, heat transfer is enhanced using the extended surface. Excessive heat is produced in machine parts in several industrial applications, which can lead to a variety of material flaws. Heat transfer through the extended surface of the apparatus is one strategy for avoiding material damage. A fin is an extended surface that is utilized to augment the rate of heat transference from the primary surface to the environment. It has extensive technological applications, namely air-cooled craft engines, compressors, nuclear reactors, heat exchangers, refrigeration, electrical and electronic apparatuses, and so on. Meanwhile, porous material fins have considerable advantages over conventional fins, and their research is one of the most comprehensive topics in the field of mass and energy transference. In the heat transferal scrutiny of permeable material fins, energy and mass transference of both solid and fluid media must be taken into account. Several analyses have been performed to explore efficient and productive methods of heat transferring through permeable finned surfaces. Ndlovu and Moitsheki8 discussed the one-dimensional heat transport and thermal aspects in a moveable porous straight fin of the uniform area of cross-section. With the impact of radiative, magnetic, and convective mechanisms, Madhura et al.9 depicted the features of the thermal field of a permeable longitudinal fin. The sinc collocation method was executed to study the thermal behavior of permeable fin by Nabati et al.10 under the influence of magnetic force. With the implementation of analytical procedures, Kundu and Yook11 determined the analytical approximation of the porous fin and thus investigated the heat transfer features of the considered fin. Considering the local thermal non-equilibrium model, Buonomo et al.12 researched the energy transfer aspects of a permeable rectangular extended surface. Implementing the spectral collocation method, Kumar et al.13 described the temperature and energy variation in a permeable trapezoidal extended surface with radiation phenomenon.

Fins with a non-uniform cross-sectional area, which contribute to a lighter structure, are recommended in airborne and space application fields over heavier rectangular-shaped fins, despite the fact that such lighter fin constructions are more complicated and costlier to produce. Aziz and Fang14 expounded on the thermal variations inside the straight fin of variable thickness. Further heat transfer aspects are discussed by considering various fin profiles namely trapezoidal, rectangular and concave. Using the DTM approach, Torabi et al.15 debriefed the thermal performance of radiative-convective concave profiled fin. The heat transference features of the concave parabolic extended surface were discussed by Kang16. Recently, Wang et al.17 employed the technique of DTM to examine the aspects of energy dissipation through a permeable fin of the inclined surface. The thermal performance and heat flow in a dovetail fin with internal heat production were probed by Goud et al.18. In the presence of convection and radiation, Jagadeesha et al.19 expounded on the thermal performance of a fully wetted semi-spherical fin using a non-Fourier heat conduction model. Several researchers have worked on solving ordinary differential equations using various techniques, including the differential transform method20,21,22,23,24, sinc collocation approach10, finite difference method25, spectral collocation method26,27, least square method28 and among others. Several of these methodologies are computationally complex because they are trial-and-error in nature or involve complicated symbolic calculations. The residual power series method (RPSM) is one of the analytical techniques which is broadly utilized to achieve an approximate solution because it does not necessitate any restrictive assumptions or linearization. This method can be employed effectively to the given problems and it is easier to achieve accurate approximate solutions without more complications. The RPSM is an innovative approach for procuring analytical Taylor series solutions for linear and nonlinear differential equations. As a result of applying the residual error notion, a series solution, as well as a truncated series solution, can be obtained. Arqub et al.29,30 applied the RPSM for solving the initial value problems. Using RPSM, Syam31 discussed the solution of the fractional-order Fredholm integrodifferential equation. Az-Zo’bi32 applied RPSM to analyze the numerical solution of the time-dependent motion of the van der Waals gas model. Refs.33,34,35,36,37,38 highlights the importance of fluid flow regarding various assumption via different geometries.

The majority of the studies were focused on analyzing the one-dimensional thermal distribution of the porous straight fin or fin with a tapered profile, as evidenced by the above investigations. Further numerical and analytical solutions are provided in other cases. Also, there are no detailed analyses with analytical solutions on the unsteady thermal distribution through a tapered inclined fin. Thus, the principal objective of this analysis is to scrutinize the unsteady temperature variance through an inclined concave porous fin with internal heating. Moreover, the temperature profile of the fin has been solved analytically using the generalized residual power series method (GRPSM).

Mathematical formulation

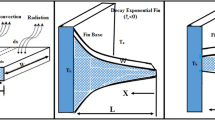
The unsteady thermal performance of permeable concave fin with convection and radiation is studied. \(L\) and \(W\) are the length and width of the permeable concave fin with base thickness \(t_{b}\). The dissipation of heat to the ambient environment occurs due to the effect of radiation and convection at \(T_{a}\). The fin which is attached to an inclined surface at an angle \(\alpha\) is considered in this analysis, as demonstrated in Fig. 1. It is assumed that the porous medium is saturated with a single phase, homogeneous, and isotropic fluid. Darcy's model characterizes the interaction of a porous medium and fluid media. Another implication involves that the fin's thickness is small in comparison to its length. The temperature inside the fin is also presumed to vary only in the x-direction, with the temperature variation in the y-direction being small enough to ignore.

Figure 1
figure 1

Physical depiction of an inclined concave parabolic fin.

Full size image

The transient energy transmission with the above-mentioned assumption is stated by the following governing equation (Torabi et al.15, and Ma et al.39):

$$\begin{aligned} \rho c_{p} t_{b} \frac{\partial T}{{\partial \tau }} & = \frac{\partial }{\partial x}\left[ {\left\{ {k_{f} \phi + k_{s} \left( {1 - \phi } \right)} \right\}t(x)\frac{\partial T}{{\partial x}}} \right] - \left( {1 - \phi } \right)h^{*} \left( {T - T_{a} } \right) + \left( {1 - \phi } \right)t(x)q^{*} (T) \\ & \quad - \frac{{\rho_{f} c_{p} gK\beta_{f} \sin \left( \alpha \right)}}{{\,\nu_{f} }}\left( {T - T_{a} } \right)^{2} - \sigma \varepsilon^{*} \left( {T^{4} - T_{a}^{4} } \right), \\ \end{aligned}$$
(1)

where \(h^{*}\) is the convective heat transfer coefficient, \(q^{*} (T)\) signifies internal heat generation, \(\rho\) is the density, \(\sigma\) indicates Stefan–Boltzmann constant, \(g\) symbolizes acceleration due to gravity, \(K\) is the permeability, \(c_{p}\) represents specific heat, and \(t(x) = \left[ {\Lambda \left( {\left( \frac{x}{L} \right)^{2} - 1} \right) + t_{b} } \right]\) is the local semi-fin thicknesses.

The internal heat generation is presumed to be a function of temperature:

$$q^{*} (T) = q_{a} \left[ {1 + \xi \left( {T - T_{a} } \right)} \right],$$
(2)

where, \(q_{a}\) denotes heat generation at ambient temperature, and \(\xi\) is the heat generation parameter. As this analysis considers a finite-length fin with an insulated tip, there will be no heat flow through the tip of the fin. Thus, the relevant boundary conditions (BCs) for Eq. (1) are:

$$\begin{aligned} T\left( {x,0} \right) & = T_{a} , \\ T\left( {L,\tau } \right) & = T_{b} , \\ \frac{\partial T}{{\partial x}}_{x = 0} & = 0. \\ \end{aligned}$$
(3)

The appropriate non-dimensional terms involved in this study are:

$$\begin{gathered} \tau^{*} = \frac{{k_{s} \tau }}{{\rho c_{p} L^{2} }},\quad k_{r} = \frac{{k_{f} }}{{k_{s} }},\quad \Theta = \frac{T}{{T_{b} }},\quad X = \frac{x}{L},\quad C = \frac{\Lambda }{{t_{b} }},\quad Nc = \frac{{h^{*} \left( L \right)^{2} }}{{k_{s} t_{b} }} \hfill \\ \Theta_{a} = \frac{{T_{a} }}{{T_{b} }},\quad Nr = \frac{{\sigma \varepsilon^{*} T_{b}^{3} \left( L \right)^{2} }}{{k_{s} t_{b} }},\quad S_{H} = \frac{{\rho_{f} c_{p} gK\beta_{f} \left( L \right)^{2} T_{b} }}{{\nu_{f} k_{S} t_{b} }}, \hfill \\ Q = \frac{{q_{a} \left( L \right)^{2} }}{{k_{s} T_{b} }},\quad \gamma = T_{b} \xi . \hfill \\ \end{gathered}$$
(4)

Equation (1) and BCs are transformed to a non-dimensional form using Eq. (2) and Eq. (4) to yield,

$$\begin{aligned} \frac{\partial \Theta }{{\partial \tau^{*} }} & = \frac{\partial }{\partial X}\left[ {\left( {k_{r} \,\varphi + \left( {1 - \phi } \right)} \right)\left( {C\left( {X^{2} - 1} \right) + 1} \right)\frac{\partial \Theta }{{\partial X}}} \right] - S_{H} \sin \left( \alpha \right)\left( {\Theta - \Theta_{a} } \right)^{2} - \left( {1 - \phi } \right)Nc\left( {\Theta - \Theta_{a} } \right) \\ & \quad - Nr\left( {\Theta^{4} - \Theta_{a}^{4} } \right) + \left( {1 - \phi } \right)\left( {C\left( {X^{2} - 1} \right) + 1} \right)Q\left[ {1 + \gamma \left( {\Theta - \Theta_{a} } \right)} \right]. \\ \end{aligned}$$
(5)

The above equation includes radiation-conduction parameter \(Nr\) which is directly associated with the surface emissivity, fin taper ratio \(C\) that describes the concave tapered profile, convection-conduction parameter \(Nc\) is the ratio of convention to conduction, internal heat production parameter \(Q\), and porosity parameter \(S_{H}\).

Simultaneously with the help of Eq. (4), Eq. (3) yields,

$$\begin{aligned} \Theta \left( {X,0} \right) & = \Theta_{a} , \\ \Theta \left( {1,\tau^{*} } \right) & = 1, \\ \left. {\frac{\partial \Theta }{{\partial X}}} \right|_{X = 0} & = 0. \\ \end{aligned}$$
(6)

Fundamentals of GRPSM

Let \(F\) be a function of two variables \(x\) and \(t\) i.e.\(F(x,t)\) and consider the following PDE,

$$\frac{\partial }{\partial t}F(x,t) + \Omega \,F(x,t) = g(x,t),\,\,\,\,\,\,x \in \Gamma, \,\,\,\,\,\,t \in [0,{\rm Z}],$$
(7)

with initial and boundary conditions,

$$\begin{gathered} F(x,0) = F_{0} (x),\,\,\,\,\,\,\,x \in \Gamma \hfill \\ F(x,t) = h(x,t),\,\,\,\,\,\,\,x \in \partial \Gamma, \,\,\,\,\,\,\,\,t \in {\rm Z}, \hfill \\ \end{gathered}$$
(8)

where, \(\Omega\) is a differential operator and \(g\) denotes the source term.

Assume that the solution of Eq. (7) has the power series in the form shown below

$$F(x,t) = \sum\limits_{i = 0}^{k} {Y_{i} (x)t^{i} ,\quad k = 0,1,2,3, \ldots }$$
(9)

Rewriting the Eq. (7) yields

$$\frac{\partial }{\partial t}F(x,t) + \Omega F(x,t) - g(x,t) = 0.$$
(10)

To evaluate the coefficient functions, \(Y_{i} (x),\,\,\,i = 0 \ldots k\), kth residual function is defined as

$${\text{Re}} s^{k} (t) = \frac{\partial }{\partial t}\left[ {\left( {Y_{0} (x) + \sum\limits_{i = 1}^{k} {Y_{i} (x)t^{i} } } \right)} \right] + \Omega \sum\limits_{i = 0}^{k} {Y_{i} (x)t^{i} - g(x,t)}.$$
(11)

Reiterating this operation to find the nth-truncated solution yields

$$F\left( {x,t} \right) = Y_{0} (x) + Y_{1} (x)t + Y_{2} (x)t^{2} + Y_{3} (x)t^{3} + \cdots.$$
(12)

Application of GRPSM

Rearrange the Eq. (5) as:

$$\begin{aligned} & \frac{\partial \Theta }{{\partial \tau^{*} }} - \frac{\partial }{\partial X}\left[ {\left( {k_{r} \,\varphi + \left( {1 - \phi } \right)} \right)\left( {C\left( {X^{2} - 1} \right) + 1} \right)\frac{\partial \Theta }{{\partial X}}} \right] + S_{H} \sin \left( \alpha \right)\left( {\Theta - \Theta_{a} } \right)^{2} + \left( {1 - \phi } \right)Nc\left( {\Theta - \Theta_{a} } \right) \\ & \quad + Nr\left( {\Theta^{4} - \Theta_{a}^{4} } \right) - \left( {1 - \phi } \right)\left( {C\left( {X^{2} - 1} \right) + 1} \right)Q\left[ {1 + \gamma \left( {\Theta - \Theta_{a} } \right)} \right] = 0. \\ \end{aligned}$$
(13)

Let the series solution be in the form

$$\Theta \left( {X,\tau^{*} } \right) = \sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} }.$$
(14)

Applying the GRPSM to Eq. (13) gives

$$\begin{aligned} {\text{Re}} s^{k} \left( {X,\tau^{*} } \right) & = \frac{\partial }{{\partial \tau^{*} }}\left( {\sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} } } \right) - \frac{\partial }{\partial X}\left[ {\left( {k_{r} \,\varphi + \left( {1 - \phi } \right)} \right)\left( {1 + C\left( {X^{2} - 1} \right)} \right)\frac{\partial }{\partial X}\left( {\sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} } } \right)} \right] \\ & \quad + S_{H} \sin \left( \alpha \right)\left( {\left( {\sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} } } \right) - \Theta_{a} } \right)^{2} + \left( {1 - \phi } \right)Nc\left( {\left( {\sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} } } \right) - \Theta_{a} } \right) + Nr\left( {\left( {\sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} } } \right)^{4} - \Theta_{a}^{4} } \right) \\ & \quad - \left( {1 - \phi } \right)\left( {1 + C\left( {X^{2} - 1} \right)} \right)Q\left[ {1 + \gamma \left( {\left( {\sum\limits_{k = 0}^{m} {\Psi_{k} \left( X \right)\left( {\tau^{*} } \right)^{k} } } \right) - \Theta_{a} } \right)} \right]. \\ \end{aligned}$$
(15)

To obtain the coefficients \(\Psi_{k} \left( X \right),\,\,k = 1,2,3, \ldots ,m\), replace \(k\)th a truncated series of \(\Theta \left( {X,\tau^{*} } \right)\) in Eq. (15), and apply the below derivative formula on \({\text{Re}} s^{k} \left( {X,\tau^{*} } \right)\) (Modanli et al.40),

$$\left. {\frac{{\partial^{h} }}{{\partial \tau^{*h} }}{\text{Re}} s^{k} \left( {X,\tau^{*} } \right)} \right|_{{\tau^{*} = 0}} = 0,\quad h = 1,2,3, \ldots ,m.$$
(16)

For simplificantion, the values for the corresponding parameters are taken as \(Nc = 2\), \(S_{H} = 0.5\), \(Nr = 3\), \(\Theta_{a} = 0.2\), \(k_{r} = 0.1\), \(C = 0.1\), \(\phi = 0.1\), \(\gamma = 0.2\), \(Q = 0.8\) and \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\). Upon substituting these values and with the use of BCs the coefficients of \(\Psi_{k} \left( X \right),\;k = 1,2,3, \ldots ,8\) are determined,

$$\Psi_{0} = {\rm M},\quad \Psi_{1} = 1,$$
(17)
$$\Psi_{3} = \Psi_{5} = \Psi_{7} = 0,$$
(18)
$$\Psi_{2} = 1.831501832\,{\rm M}^{4} - 0.5963858364 + 0.9587301587\,{\rm M} + 0.1526251526\,{\rm M}^{2}$$
(19)
$$\begin{aligned} \Psi_{4} & = { }0.06695131846\,{\rm M}^{2} + 1.388721169\,{\rm M}^{4} - 0.07102258678 + 0.08383240328\,{\rm M} \\ & \quad + 0.2795332466\,{\rm M}^{5} - 0.7204230222\,{\rm M}^{3} + 2.236265973\,{\rm M}^{7} \\ \end{aligned}$$
(20)
$$\begin{aligned} \Psi_{6} & = - 0.01045231395\,{\rm M} + 0.001392072268 - 1.923825243\,{\rm M}^{6} + 0.6257357983\,{\rm M}^{8} \\ & \quad + 3.549628529\,{\rm M}^{10} - 0.8906991152\,{\rm M}^{3} + 0.5878481440\,{\rm M}^{4} + 0.2718739855\,{\rm M}^{2} \\ & \quad + 0.3198549028\,{\rm M}^{5} + 3.321141670\,{\rm M}^{7} \\ \end{aligned}$$
(21)
$$\begin{aligned} \Psi_{8} & = - 0.05685639053{\rm M} + 0.0004730083722 + 5.751018328{\rm M}^{13} - 4.073041686{\rm M}^{9} \\ & \quad + 1.318685879{\rm M}^{11} - 3.151272005{\rm M}^{6} + 1.069742989{\rm M}^{8} + 7.101219309{\rm M}^{10} \\ & \quad - 0.4787022153{\rm M}^{3} + 0.09124498829{\rm M}^{4} + 0.3033104496{\rm M}^{2} + 1.101500411{\rm M}^{5} \\ & \quad + 2.140222196{\rm M}^{7}. \\ \end{aligned}$$
(22)

Express the above coefficients in a truncation series and \({\text{M}} = 0.5937942627\) is the value obtained with the help of BC. Using the achieved \(k\)th truncated series in Eq. (14), the final series solution of the fin problem is represented as

$$\begin{aligned} \Theta \left( {X,\tau^{*} } \right) & = 0.5937942627 + 0.2544108558\,\left( {\tau^{*2} } \right) + 0.1030198229{ }\left( {\tau^{*} } \right)^{4} \\ & \quad + 0.03238695124{ }\left( {\tau^{*} } \right)^{6} + 0.01234307481{ }\left( {\tau^{*} } \right)^{8} + \cdots \cdots \cdots. \\ \end{aligned}$$
(23)

Discussion of results

An internal heat generation, natural convection, and radiation impact are taken into account in formulating the unsteady thermal model of an inclined concave porous fin. Equation (1) expresses the corresponding balanced heat equation and is converted to a PDE using dimensionless terms along with BCs. The obtained equation discloses that dimensionless parameters effect the thermal distribution of a porous fin. Subsequently, Eq. (5) is derived analytically using the elementary properties of the proposed technique. For the analysis of the inclination effect, Table 1 is provided to witness the variation in the transient thermal profile \(\Theta \left( {X,\tau^{*} } \right)\) of the inclined porous fin with respect to different angles of inclination \(\alpha\). It is detected from this table, that thermal distribution diminishes from base to tip of the porous fin for all non-dimensional variables considered in the study \(Nc = 1\), \(S_{H} = 10\), \(Nr = 1\), \(\Theta_{a} = 0.1\), \(k_{r} = 0.1\), \(C = 0.1\), \(\phi = 0.1\), \(\gamma = 0.1\), \(Q = 0.8\) at different values of inclination angle. The thermal profile signifies greater thermal distribution at \(\alpha = 0\), resulting in a lower rate of heat transfer. Meanwhile, as the \(\alpha\) value is modified (\(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6},\,{\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-\nulldelimiterspace} 3},{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\)), the thermal profile of the fin reveals decreasing characteristics at all locations of fin length. The consequence of the aforementioned dimensionless parameters on the thermal gradient \(\Theta \left( {\tau^{*} ,X} \right)\) of the fin is graphically examined in this section. The nonlinear PDE (Eq. (5)) is solved using the finite difference method (FDM) technique in the domain \(0 \le X \le L\) and \(0 \le \tau^{*} \le T\). Along with uniform mesh, the finite-difference approximation is applied in the direction of \(X\) and the step size of time and space domains are chosen as \(\Delta \tau^{*} = \Delta X = 0.001\). Further, the present analysis (GRPSM) is compared with the numerical result (FDM) as displayed in Fig. 2 and they are found to be in excellent agreement. The significance of dimensionless parameters on the temperature deviance of the fin has been portrayed in Figs. 3, 4, 5, 6 and 7.

Table 1 Variation of \(\Theta \left( {X,\tau^{*} } \right)\) for various angle of inclination at \(\tau^{*} = 0.5\).
Full size table
Figure 2
figure 2

Validation of the present result with the numerical method.

Full size image
Figure 3
figure 3

(a) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various \(Nc\) values (b) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various \(Nr\) values.

Full size image
Figure 4
figure 4

(a) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various \(\Theta_{a}\) values (b) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various \(S_{H}\) values.

Full size image
Figure 5
figure 5

(a) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various \(Q\) values (b) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various τ* values.

Full size image
Figure 6
figure 6

(a) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for \(\tau^{*} = 0.1\) (b) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) for various \(\tau^{*} = 0.3\).

Full size image
Figure 7
figure 7

(a) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) of solid non-porous fin (b) Nature of \(\Theta \left( {X,\tau^{*} } \right)\) of porous fin.

Full size image

The impact of convective parameter \(Nc\) on the temperature distribution of the concave fin is seen in Fig. 3a for \(S_{H} = 0.5\), \(Nr = 1\), \(\Theta_{a} = 0.1\), \(k_{r} = 0.1\), \(\phi = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), \(Q = 0.8\), and \(\tau^{*} = 0.5\) by considering different \(C\) values (\(C = 0.1\,{\text{and}}\,C = 0.3\)). It is detected that with a rise in the convective parameter (\(Nc = 1,\,3,\,5\)) thermal profile decreases. This is due to the effect of the natural convection on the concave surface of the fin. The convection will carry the heat on fin surface and hence helps in decreasing the heat and aids in fin cooling. With all the considered parameter \(Nc = 1\), \(S_{H} = 0.6\), \(\Theta_{a} = 0.2\), \(k_{r} = 0.1\), \(\phi = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), \(Q = 0.8\), Fig. 3b displays the impact of radiative parameter \(Nr\) on the thermal performance of the concave fin. The radiative parameter exhibits the same nature as that of the convective parameter, i.e., a decrease in temperature profile with increase in \(Nr\) (2, 4, 6). The radiation effect increases the transfer of heat from fin surface to the surrounding. Therefore, the reduction in temperature has been observed with rising in radiation parameter. The significance of ambient temperature \(\Theta_{a} \left( {0,\,0.3,\,0.5} \right)\) on the fin thermal field of a concave inclined porous fin with \(Nc = 1\), \(S_{H} = 0.2\), \(Nr = 1\), \(k_{r} = 0.1\), \(\phi = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), \(Q = 0.8\), and \(\tau^{*} = 0.5\) is exhibited in Fig. 4a. The enhancement in ambient temperature results in an increase in thermal profile. This is because, \(\Theta_{a}\) is the ratio of surrounding temperature to base temperature. Hence, with augment in \(\Theta_{a}\) there is a decrease in the transmission of heat from fin surface to surrounding which leads to the increase in thermal profile. By setting \(Nc = 2\), \(Nr = 1\), \(\Theta_{a} = 0.3\), \(k_{r} = 0.1\), \(\phi = 0.1\),\(\gamma = 0.1\) , \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), \(Q = 0.7\), and \(\tau^{*} = 0.5\), the effect of \(S_{H}\) on \(\Theta\) of the fin has been revealed in Fig. 4b. The enhancement in \(S_{H}\) (\(1,\,3,\,5\)) leads to the reduction in the temperature profile. This is due to the fact that the porosity parameter helps in better interaction of surrounding air with the pores of the fin. Hence the porosity parameter helps in the fin cooling effect. The consequences of heat generation parameter \(Q\) on the \(\Theta\) of the fin have been depicted in Fig. 5a with \(Nc = 1\), \(S_{H} = 0.3\), \(Nr = 1\), \(\Theta_{a} = 0.2\), \(k_{r} = 0.1\), \(\phi = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), and \(\tau^{*} = 0.5\). Here the augment in \(Q\) (\(0,\,0.4,\,0.8\)) enlarges the thermal value along the axial length of the fin because of the presence of internal heat within the fin. The internal heat enhances the fin surface temperature therefore it decreases the rate of cooling from the surface of the fin. Figure 5b explicates the impact of \(\tau^{*}\) on \(\Theta\) of the concave porous fin. As the \(\tau^{*}\) (\(0.2,\,0.3,\,0.4\)) values increase, the temperature improves remarkably under the consideration of \(Nc = 1\), \(S_{H} = 0.1\), \(Nr = 1\), \(\Theta_{a} = 0.1\), \(k_{r} = 0.1\), \(\phi = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), \(Q = 0.8\). Figure 6a and b demonstrate the variation in the unsteady thermal distribution of the concave inclined porous fin as a function of time in a three-dimensional (3D) plot for \(Nc = 1\), \(S_{H} = 0.1\), \(Nr = 1\), \(\Theta_{a} = 0.1\), \(k_{r} = 0.1\), \(C = 0.3\), \(\phi = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), and \(Q = 0.8\). In particular, in Fig. 6a, the value of \(\tau^{*}\) is picked as 0.1, and for this value, a decrement in thermal variation has been discovered, whereas an increment in thermal variation is recognized for \(\tau^{*} = 0.3\), as exhibited in Fig. 6b. A comparison of the thermal profile values of the concave inclined solid and porous fin has been performed to uphold the significance of modeled fin problem. For a better interpretation of the thermal variation of the concave inclined porous and solid fin, Fig. 7a and b are plotted when the parameter values are set to \(Nc = 1\), \(Nr = 1\), \(\Theta_{a} = 0.1\), \(k_{r} = 0.1\), \(C = 0.1\), \(\gamma = 0.1\), \(\alpha = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}\), \(Q = 0.8\), and \(\tau^{*} = 0.5\). At \(X = 0\), the thermal field value of the solid fin \(\left( {S_{H} = \phi = 0} \right)\) is comparatively higher than the porous fin \(\left( {S_{H} = 10,\,\phi = 0.1} \right)\) and the same behavior is observed at all the considered values of \(X\) (0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6). Thus, it is deduced that the porous fin helps in thermal dissipation and thereby provides a higher heat transfer rate. The effect of the fin taper ratio is recognizable in all of the aforementioned thermal investigation cases, and it is determined that the temperature inside the fin decreases as the scale of \(C\) (0.1, 0.3) increases.

Conclusions

The current study explains transient thermal dispersion in a concave permeable fin exposed to convective-radiative heat transfer. The governing equation is nondimensionalized by employing non-dimensional terms, and the arising PDE is solved analytically using the GRPSM. The consequences of significant non-dimensional factors on the temperature gradient are also depicted utilizing graphical portrayal. The following are some of the most significant study results of the present research:

  • Unlike prior investigation, the heat transfer performance of the fin is effected not only by the radiation and convection mechanisms but also by the fin taper ratio, and inclination of the primary surface.

  • The thermal dispersal in the porous fin is elevated in increasing time.

  • With a greater level of fin taper ratio, the fin undergoes diminishing thermal dispersal.

  • As the convection-conduction and porosity parameter values rise, the thermal dispersal in the fin declines.

  • The temperature profile of the fin exhibits an enhanced nature for the raised heat-generating parameter.

  • The thermal dispersal in the fin drops as the magnitude of the radiation-conduction attribute rises.

  • It may be highly beneficial to a designer to select the tapered fin design with an inclined vertical surface for thermal effectiveness in a practical application such as latent heat thermal energy storage systems.

  • GRPSM provides an analytical solution for nonlinear differential equations and the obtained outcomes in this research work are in close agreement with numerical ones. The exactness of the proposed method signifies that GRPSM is an alternative to other techniques for solving nonlinear PDEs.

Data availability

All the data are clearly available in the manuscript.