Introduction

Supercritical carbon dioxide (ScCO2) is a fluid above its critical point. It has physical properties (density, diffusivity, viscosity and surface tension) intermediate to that of gas and liquid1,2. ScCO2 has been used as a solvent in various process applications, because it has gas like diffusivity and liquid like density with low viscosity and surface tension1,3,4,5. The major applications are in drug particle micronization, food processing, textile dyeing, ceramic coating, extraction and many more4,6,7,8,9,10,11,12. Although, several supercritical fluids are utilized as solvent in process industry, ScCO2 is the most desirable solvent8,13,14,15,16,17. In general, phase equilibrium information is necessary to implement supercritical fluid technology (SFT)6,7,9. The solubility is the basic information for the design and development of SFT. In literature, solubility of many drug solids in ScCO2 is readily available18,19,20,21,22,23,24,25,26,27,28,29,30, however, the solubility of empagliflozin has not been reported, therefore in this work for the first time, its solubility in ScCO2 has been measured. This data may be used in the particle micronization process using ScCO2. The molecular formula of empagliflozin is C23H27 ClO7 and its molecular weight is 450.91. The chemical structure is shown in Fig. 1.

Figure 1
figure 1

Empagliflozin chemical structure.

Full size image

Empagliflozin is an inhibitor of sodium-glucose co-transporter-2 (SGLT2), the transporters primarily responsible for the re-absorption of glucose in the kidney. Further, it is useful in reducing the risk of cardiovascular death in adults with type 2 diabetes mellitus and cardiovascular disease31. Sufficient drug dosage is very essential for those treatments and this is achieved through a proper particle size. Therefore, the present study is quite useful in particle micronization using ScCO2. Solubility measurement at each desired condition is very cumbersome and hence, there is a great need to develop a model that correlates/predicts the solubility32. Recent developments such as machine learning methods may be considered with the improvement of artificial intelligence prediction methods for the data correlation33,34,35. However, in general, the solubility models are classified into five types; however, only three are user friendly, and they are equation of state, density-based and mathematical models36. Directly or indirectly all of them are derived based on thermodynamic frame work. The derived models make use of the basic concepts related to phase equilibrium criteria (solid–gas or solid–liquid), solvent–solute association theory, dilute solution theory, solution theory and Wilson model or any other model37. In fact, most of the literature models correlate the solubility of the solid solutes in ScCO2 quite well. A solid–gas equilibrium models need the critical properties and vapour pressure of the solute, while these properties are rarely available in literature, due to this, the group contribution methods are commonly used38. On the other hand, the solid–liquid equilibrium (SLE) criterion requires an appropriate model for activity coefficient calculation. A recent study reveals that SLE model in combination with Van Laar activity coefficient model can be a simple approach in model development, but this method resulted in an implicit expression in terms of mole fraction38,39. Therefore, there is a need to develop an explicit solubility model and hence, this task is taken up in this work.

The main motives of this study were in two levels. In the first level, empagliflozin solubility in ScCO2 was determined and in the second level, a new explicit solubility model was developed based on solid–liquid equilibrium criterion in combination with Wilson activity coefficient model for the activity coefficient calculation.

Experimental

Materials

Gaseous CO2 (purity > 99.9%) was obtained from Fadak company, Kashan (Iran), empagliflozin (CAS Number: 864070-44-0, purity > 99%) was purchased from Amin Pharma company, and dimethyl sulfoxide (DMSO, CAS No. 67-68-5, purity > 99%) was provided from Sigma Aldrich company. Table 1 indicates all the information about the chemicals utilized in this work.

Table 1 Some physicochemical properties of the used materials.
Full size table

Experiment details

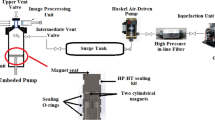
The detailed discussion of the solubility apparatus and equilibrium cell has been presented in our earlier studies (Fig. 2)19,25,40,41. However, a brief description about the apparatus is presented in this section. This method may be classified as an isobaric-isothermal method42. Each measurement was carried out with high precision and temperatures and pressures were controlled within ± 0.1 K and ± 0.1 MPa, respectively. For all measurement, 1 g of empagliflozin drug was used. As mentioned in our previous works, the equilibrium was observed within 60 min. After equilibrium, 600 µL saturated ScCO2 sample was collected via 2-status 6-way port valve in a DMSO preloaded vial. After discharging 600 µL saturated ScCO2, the port valve was washed with 1 ml DMSO. Thus, the total saturation solution was 5 ml. Each measurement was repeated thrice and their average values were reported. Mole fraction is obtained as follows:

$$ y_{2} = \frac{{n_{drug} }}{{n_{drug} + n_{{CO_{2} }} }} $$
(1)

where \({n}_{\text{solute}}\) is the moles number of the drug, and \({n}_{{\text{CO}}_{2}}\) is the moles number of CO2 in the sampling loop.

Figure 2
figure 2

Experimental setup for solubility measurement, E1—CO2 cylinder; E-2—Filter; E-3—Refrigerator unit; E-4—Air compressor; E-5—High pressure pump; E-6—Equilibrium cell; E-7—Magnetic stirrer; E-8—Needle valve; E-9—Back-pressure valve; E-10—Six-port, two position valve; E-11—Oven; E-12—Syringe; E13—Collection vial; E-14—Control panel.

Full size image

Further, the above quantities are given as:

$${n}_{\text{solute}}=\frac{{C}_{s}\cdot {V}_{s}}{{M}_{s}}$$
(2)
$${n}_{{\text{CO}}_{2}}=\frac{{V}_{1}\cdot \rho }{{M}_{{\text{CO}}_{2}}}$$
(3)

where \({C}_{\text{s}}\) is the drug concentration in saturated sample vial in g/L. The volume of the sampling loop and vial collection are V1(L) = 600 \(\times \) 10–6 m3 and Vs(L) = 5 \(\times \) 10–3 m3, respectively. The \(M_{s}\) and \(M_{{\text{CO}_{2} }}\) are the molecular weight of drug and CO2, respectively. Solubility is also described as

$$ S = \frac{{C_{S} V_{s} }}{{V_{1} }} $$
(4)

The relation between S and \(y_{2}\) is

$$ S = \frac{{\rho M_{s} }}{{M_{{\text{CO}_{2} }} }}\frac{{y_{2} }}{{1 - y_{2} }} $$
(5)

A UV–Visible spectrophotometer (Model UNICO-4802) and DMSO solvent were used for the measurement of empagliflozin solubility. The samples were analyzed at 276 nm.

Existing and new models and their correlations

In this section, the details of various solubility models are presented along with a new explicit solubility model.

Existing models

Alwi–Garlapati model (three parameters model)43

It is one of the latest models for the solubility correlation. It is mathematically explained as

$$ y_{2} = \frac{1}{{\rho_{r} T_{r} }}\exp \left( {A_{1} + \frac{{B_{1} }}{{T_{r} }} + C_{1} \rho_{r} } \right) $$
(6)

where \(A_{1} - \;C_{1}\) are model constants.

Bartle et al., model (three parameters model)44

It is an empirical model and mathematically stated as:

$$ \ln \left( {\frac{{y_{2} P}}{{P_{ref} }}} \right) = A_{2} + \frac{{B_{2} }}{T} + C_{2} \left( {\rho - \rho_{ref} } \right) $$
(7)

where \(A_{2} - C_{2}\) are model constants. From parameter \(B_{2}\), one can estimate sublimation enthalpy using the relation, \(\Delta_{sub} H = - B_{2} R\), in which R is universal gas constant.

Bian et al., model (five parameters model)45

It is an empirical model and mathematically formulated as:

$$ y_{2} = \rho_{1}^{{\left( {A_{3} + B_{3} \rho_{1} } \right)}} \exp \left( {{{C_{3} } /T} + D_{3} {{\rho_{1} } / T} + E_{3} } \right) $$
(8)

where \(A_{3} - E_{3}\) are model constants.

Chrastil model (three parameters model)46

It is a semi-empirical model and mathematically stated as:

$$ c_{2} = \rho_{1}^{\kappa } \exp \left( {A_{4} + \frac{{B_{4} }}{T}} \right) $$
(9)

where \(\kappa ,A_{4} \;{\text{and}}\;B_{4}\) are model constants.

In terms of mole fraction, it is written as47:

$$ y_{2} = \frac{{\left( {\rho_{1} } \right)^{\kappa - 1} \exp \left( {A_{4} + \frac{{B_{4} }}{T}} \right)}}{{\left[ {1 + \left( {\rho_{1} } \right)^{\kappa - 1} \exp \left( {A_{4} + \frac{{B_{4} }}{T}} \right)} \right]}} $$
(9a)

Garlapati–Madras model (five parameters model)48

It is a mathematical model and mathematically formulated as

$$ \ln \left( {y_{2} } \right) = A_{5} + (B_{5} + C_{5} \rho_{1} )\ln \left( {\rho_{1} } \right) + \frac{{D_{5} }}{T} + E_{5} \ln \left( {\rho_{1} T} \right) $$
(10)

where \(A_{5} - E_{5}\) are model constants.

Kumar–Johnstone model (three parameters model)49

It is a semi empirical model and mathematically described as:

$$ \ln \left( {y_{2} } \right) = A_{6} + B_{6} \rho + {C_{6}} /T $$
(11)

where \(A_{6} - C_{6}\) are model constants.

Mahesh–Garlapati model (three parameters model)39

It is one of the latest models. It is based on degree of freedom and mathematically stated as:

$$ \ln \left( {y_{2} } \right) = A_{7} + B_{7} \rho_{r} T_{r} + C_{7} \rho_{r} T_{r}^{3} $$
(12)

where \(A_{7} - C_{7}\) are model constants.

Mendez–Teja model (three parameters model)50

It is a semi-empirical model and mathematically explained as:

$$ T\ln \left( {y_{2} P} \right) = A_{8} + B_{8} \rho + C_{8} T $$
(13)

where \(A_{8} - C_{8}\) are model constants.

Sodefian et al., model (six parameters model)40

It is a mathematical model and stated as:

$$ \ln \left( {y_{2} } \right) = A_{9} + \frac{{B_{9} P^{2} }}{T} + C_{9} \ln \left( {\rho_{1} T} \right) + D_{9} \left( {\rho_{1} \ln \left( {\rho_{1} } \right)} \right) + E_{9} P\ln \left( T \right) + F_{9} \frac{{\ln \left( {\rho_{1} } \right)}}{T} $$
(14)

where \(A_{9} - F_{9}\) are model constants.

Reformulated Chrastil model (three parameters model)47,51

It is a semi-empirical model and mathematically explained as:

$$ y_{2} = \left( {\frac{{RT\rho_{1} }}{{M_{CF} f^{ \cdot } }}} \right)^{{\kappa^{\prime} - 1}} \exp \left( {A_{11} + \frac{{B_{11} }}{T}} \right) $$
(15)

where \(\kappa^{\prime},A_{10} \;{\text{and}}\;B_{10}\) are model constants.

Tippana–Garlapati model (six parameters model)52

It is a degree of freedom model and mathematically stated as:

$$ y_{2} = \left( {A_{12} + B_{11} P_{r} + C_{11} P_{r}^{2} } \right)T_{r}^{2} + (D_{11} + E_{11} P_{r} + F_{11} P_{r}^{2} ) $$
(16)

where \(A_{11} - F_{11}\) are model constants.

New model

According to solid–liquid phase equilibrium criteria, the fugacity of the solute in the solid phase and liquid phase is equal at equilibrium. The liquid phase is considered as an expanded liquid phase of ScCO2. At equilibrium, the solubility may be expressed as53,54,55,56,57

$$ y_{2} = \frac{1}{{\gamma_{2}^{\infty } }}\frac{{f_{2}^{S} }}{{f_{2}^{L} }} $$
(17)

where \(\gamma_{2}^{\infty }\) is drug activity coefficient at infinitesimal dilution in ScCO2 and \(f_{2}^{S}\) and \(f_{2}^{L}\) are fugacities of drug in the solid and ScCO2 phases, respectively. The \({f_{2}^{S} }/{f_{2}^{L} }\) ratio may be expressed as follows:

$$ \ln \left( {\frac{{f_{2}^{S} }}{{f_{L}^{L} }}} \right) = \frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right) - \int\limits_{{T_{m} }}^{T} {\frac{1}{{RT^{2} }}} \left[ {\int\limits_{{T_{m} }}^{T} {\left[ {\Delta C_{p} } \right]dT} } \right]dT $$
(18)

where,\(\Delta C_{p}\) is heat capacity difference of the drug in solid phase and that of SCCO2 phase. The terms that include △Cp is much smaller than the term that has \(\Delta H_{2}^{m}\)58, thus leaving △Cp term yields a much simpler expression for fugacity ratio as:

$$ \ln \left( {\frac{{f_{2}^{S} }}{{f_{L}^{L} }}} \right) = \frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right) $$
(19)

Combining Eq. (19) with Eq. (17) give the expression for the solubility model (Eq. (20)).

$$ y_{2} = \frac{1}{{\gamma_{2}^{\infty } }}\exp \left[ {\frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right)} \right] $$
(20)

In order to use Eq. (20), the appropriate model for \(\gamma_{2}^{\infty }\) is essential.

In this work, the required activity coefficient is obtained from Wilson activity coefficient model56 at infinite dilution and it is given by the Eq. (21).

$$ \gamma_{2}^{\infty } = \exp \left[ { - \ln \left( {\lambda_{21} } \right) + 1 - \lambda_{12} } \right] $$
(21)

where \(\lambda_{12} = \left( {{{V_{2} }/ {V_{1} }}} \right)\exp \left( { - {{a_{12} } /{RT}}} \right)\) and \(\lambda_{21} = \left( {{{V_{1} } / {V_{2} }}} \right)\exp \left( { - {{a_{21} } /{RT}}} \right)\), \(V_{1}\) and \(V_{2}\) are molar volumes of solvent and solute, respectively.

When \(\rho_{1} = {1 / {V_{1} }}\), the final expression for the infinite dilution activity coefficient is obtained as:

$$ \gamma_{2}^{\infty } = \exp \left[ {1 + \ln \left( {\rho_{1} V_{2} } \right) + \frac{{a_{21} }}{RT} - \rho_{1} V_{2} \exp \left( {\frac{{ - a_{12} }}{RT}} \right)} \right] $$
(22)

The quantities \(a_{12}\) and \(a_{21}\) are assumed to be functions of reduced solvent density57, and molar volume of the solute is assumed as a constant value. In this work, \(a_{12}\) and \(a_{21}\) are assumed to have the following form:

$$ a_{12} = A\left( {\rho_{r} } \right)^{B} $$
(23)
$$ a_{21} = C\left( {\rho_{r} } \right)^{D} $$
(24)

Combining Eqs. (22), (23) and (24) with Eq. (20), give the following new explicit solubility model:

$$ y_{2} = {{\exp \left[ {\frac{{\Delta H_{2}^{m} }}{RT}\left( {\frac{T}{{T_{m} }} - 1} \right)} \right]} / {\exp \left[ {1 + \ln \left( {\rho_{1} V_{2} } \right) + \frac{{A\left( {\rho_{r} } \right)^{B} }}{RT} - \rho_{1} V_{2} \exp \left( {\frac{{ - C\left( {\rho_{r} } \right)^{D} }}{RT}} \right)} \right]}} $$
(25)

Equation (25) has four temperature independent adjustable variables namely \(A\),\(B\),\(C\) and \(D\).

Equation of state (EoS) model

The solubility of drug i (solute) in ScCO2 (solvent) is expressed as59,60,61:

$$ {\text{y}}_{{\text{i}}} = \frac{{P_{i}^{S} \hat{\varphi }_{i}^{S} }}{{P\hat{\varphi }_{i}^{{ScCO_{2} }} }}\exp \left[ {\frac{{\left( {P - P_{i}^{S} } \right)V_{S} }}{RT}} \right] \, $$
(26)

where \(P_{i}^{s}\) is the sublimation pressure of the pure solid at system temperature T, P is the system pressure,\(V_{s}\) is the molar volume of the pure solid, R is the universal gas constant. The fugacity coefficient of the pure solute at saturation (\(\hat{\varphi }_{i}^{S}\)) is usually taken to be unity. In this work, the fugacity coefficient of the solute in the supercritical phase \(\hat{\varphi }_{i}^{{ScCO_{2} }}\) is calculated using EoS along with KMmr57. The expression used for calculation of \(\hat{\varphi }_{i}^{{ScCO_{2} }}\) is obtained from the following basic thermodynamic relation60:

$$ \ln \left( {\hat{\varphi }_{i}^{{ScCO_{2} }} } \right) = \frac{1}{RT}\int\limits_{v}^{\infty } {\left[ {\left( {\frac{\partial P}{{\partial N_{i} }}} \right)_{{T,V,N_{j} }} - \frac{RT}{v}} \right]} dv - \ln Z $$
(27)

The expression for \(\hat{\varphi }_{i}^{{ScCO_{2} }}\) is

$$ \begin{aligned} \ln \left( {\hat{\varphi }_{i}^{{ScCO_{2} }} } \right) & = \ln \left( {\frac{v}{{v - b}}} \right) + \left( {\frac{{2\sum {x_{j} b_{{ij}} - b} }}{{v - b}}} \right) - \ln \left( Z \right) \hfill \\ & \quad + \left( {\frac{{a\left( {2\sum {x_{j} b_{{ij}} - b} } \right)}}{{b^{2} RT^{{3/2}} }}} \right)\left[ {\ln \left( {\frac{{v + b}}{v}} \right) - \frac{b}{{v + b}}} \right]\left( {3\alpha ^{{1/2}} {{\left( {\sum {x_{j} a_{{ij}}^{{2/3}} b_{{ij}}^{{1/3}} } } \right)} / {b^{{1/2}} }} - \alpha ^{{2/3}} \left( {{{\sum {x_{j} b_{{ij}} } } / {b^{{3/2}} }}} \right)} \right)/bRT^{{3/2}} \hfill \\ \end{aligned} $$
(28)

\({\text{where}}\) \(\alpha = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} a_{{ij}}^{{2/3}} } } b_{{ij}}^{{1/3}} \)

and the associated mixing rules are:

$$ a = \frac{{\left( {\sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} a_{{ij}}^{{2/3}} b_{{ij}}^{{1/3}} } } } \right)^{{3/2}} }}{{\left( {\sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} b_{{ij}}^{{1/2}} } } } \right)^{{1/2}} }}$$
(29)
$$ b = \sum\limits_{i}^{n} {\sum\limits_{j}^{n} {x_{i} x_{j} b_{ij} } } $$
(30)
$$ a_{ij} = \left( {1 - k_{ij} } \right)\sqrt {a_{ii} a_{jj} } $$
(31)
$$ b_{{ij}} = \left( {1 - l_{{ij}} } \right)\frac{{\left( {b_{{ii}}^{{^{{1/3}} }} + b_{{jj}}^{{1/3}} } \right)^{3} }}{8} $$
(32)

The main reason for considering RKEoS is that it has only two adjustable constants \(k_{ij}\) and \(l_{ij}\).

All the models (density-based, new and RKEoS models) are correlated with the following objective function58:

$$ OF = \sum\limits_{i = 1}^{N} {\frac{{\left| {y_{2i}^{\exp } - y_{2i}^{calc} } \right|}}{{y_{2i}^{\exp } }}} $$
(33)

The regression ability of a model is indicated in terms of an average absolute relative deviation percentage (AARD %).

$${\text{AARD }}\left( \% \right){\text{ }} = \left( {{{100} / {N_{i} }}} \right)\sum\limits_{{i = 1}}^{N} {\frac{{\left| {y_{{2i}}^{{\exp }} - y_{{2i}}^{{cal}} } \right|}}{{y_{{2i}}^{{\exp }} }}}$$
(34)

For the regression, fminsearch (MATLAB 2019a®) algorithm has been used.

Results and discussion

Table 1 shows some physicochemical properties of the used materials. Empagliflozin solubility in ScCO2 is reported at various temperatures (T = 308 to 338 K) and pressures (P = 12 to 27 MPa). Table 2 indicates the solubility data and ScCO2 density. The reported ScCO2 density is obtained from the NIST data base. Figure 3 shows the effect of pressure on various isotherms. The cross over region is observed at 16.5 MPa. From Fig. 3, below the cross over region, solubility decreases with increase in temperature, and on the other hand, above the cross over region, the solubility increases with increase in temperature. The EoS model requires critical properties which are computed with standard group contribution methods based on the chemical structure62,63,64,65. The summary of the critical properties computed are shown in Table 3. Figure 4 presents the self-consistency of the measured data with MT model.

Table 2 Solubility of crystalline empagliflozin in ScCO2 at various temperatures and pressures.
Full size table
Figure 3
figure 3

Empagliflozin solubility in ScCO2 vs. pressure.

Full size image
Table 3 Critical and physical properties of empagliflozin and CO2.
Full size table
Figure 4
figure 4

Self-consistency plot based on MT model.

Full size image

The density-based models considered in this work have different number of adjustable parameters. These parameters range from three to six numbers. The regression results of all the models are indicated in Tables 4 and 5. The correlating ability of the models is depicted in Figs. 5, 6, 7, 8, 9, 10, 11. From the results, it is clear that all the models are able to correlate the data reasonably well and maximum AARD% is observed to be 10.4%. It is believed that, more parameter models are able to correlate the data more accurately. Sodefian et al., model is able to correlate the data with AARD = 5.84% and Akaike’s information criterion (AIC = − 637.59) (more relevant information is presented in the following section). Among density models, Bian et al., model (five parameters model) is able to correlate the data well and corresponding AARD% is 5.1%. Interestingly, Chrastil (three parameters model) and Reformulated Chrastil models (three parameters model) are also able to correlate the data quite well. Further, Chrastil and Reformulated Chrastil models are able to provide the total enthalpy. Whereas, Bartle et al., model parameters are able to provide sublimation enthalpy of the empagliflozin drug. From the magnitude difference between the total and sublimation enthalpies, a solvation enthalpy is calculated. These results are reported in Table 6.

Table 4 Correlation constants for the exiting empirical models.
Full size table
Table 5 Calculated result for the new model and RKEoS + Kwak-Mansoori mixing rule model.
Full size table
Figure 5
figure 5

Empagliflozin solubility vs. ScCO2 density. Solid lines and broken lines are calculated solubilities with Chrastil and Reformulated Chrastil models, respectively.

Full size image
Figure 6
figure 6

Empagliflozin solubility vs. ScCO2 density. Solid lines and broken lines are calculated solubilities with KJ and Bartle et al., models, respectively.

Full size image
Figure 7
figure 7

Empagliflozin solubility vs. ScCO2 density. Solid lines and broken lines are calculated solubilities with Alwi–Garlapati and Mahesh–Garlapati models, respectively.

Full size image
Figure 8
figure 8

Empagliflozin solubility vs. ScCO2 density. Solid lines and broken lines are calculated solubilities with Bian et al., and Garlapati–Madras models, respectively.

Full size image
Figure 9
figure 9

Empagliflozin solubility vs. ScCO2 density. Solid lines and broken lines are calculated solubilities with Tippana–Garlapati and Sodeifian et al., models, respectively.

Full size image
Figure 10
figure 10

Empagliflozin solubility vs. ScCO2 density. Solid lines are calculated solubilities with new model.

Full size image
Figure 11
figure 11

Empagliflozin solubility vs. pressure. Solid lines are calculated solubilities with RKEoS + KM mixing rule.

Full size image
Table 6 Computed thermodynamic properties.
Full size table

A new explicit solubility model based on solid–liquid equilibrium criteria combined with Wilson activity coefficient model corresponding to infinitesimal dilution is derived. The new model has four parameters \(A\), \(B\), \(C\) and \(D\). While regression, new model parameters are treated as temperature independent and solid molar volume is kept constant. The new model requires melting point, melting enthalpy and molar volume of empagliflozin drug, and these values are obtained from literature and group contribution methods. From literature31, the melting point of empagliflozin drug (426.1 K), molar volume (3.2699 × 10–4 m3/mol) and melting enthalpy (60.238 kJ/mol) are calculated based on literature, Immirzi and Perini63 and Jain et al., methods66, respectively. The new model makes use of objective function given in Eq. (33). Similarly, RKEoS along KMmr correlations are established with the help of critical properties given in Table 3 (temperature independent correlations). The optimization results of the new solubility and RKEoS models are indicated in Table 5.

In order to examine the ability of models for correlating the solubility data, AIC is applied67,68,69,70. When the data number is less than < 40, the corrected AIC (AICc) is used.

$$ AIC_{c} = AIC + \frac{{2Q\left( {Q + 1} \right)}}{N - Q - 1} $$
(35)

where AIC, N, \(Q\) and SSE are \(N\;\ln \left( {{{SSE} / N}} \right) + 2Q\), the number of observations, the number of adjustable parameters of the model and the error sum of squares, respectively. According to AICc criterion, the best model has the least AICc value. Table 7 shows AICc values for various models considered in this study. In terms of AICc, all the models are able to correlate the data closely. However, Reformulated Chrastil model has AICc value (− 637.02), hence it is treated as the best model and at the same time, Tippana–Garlapati model has the highest AICc value (− 621.69), therefore, it is considered as a poorly correlating model. Three parameters models namely Chrastil, Alwi–Garlapati and Mendez–Teja models have AICc values − 636.95, − 635.3 and − 635.4, respectively. The new model which has four parameters, indicating comparable performance with the best model (AICc value of − 637.24).

Table 7 Statistical quantities (SSE, RMSE, AIC and AICc) of various models.
Full size table

Conclusion

Solubilities of empagliflozin in ScCO2 at temperatures (T = 308–338 K) and pressures (P = 12–27 MPa) were reported for the first time. The measured solubility in terms of mole faction ranged from 5.14 × 10–6 to 25.9 × 10–6. The data was successfully correlated with several models, Bian et al., model (AARD = 5.1%) was observed to be the best model in correlating the solubility data. All the models are able correlate the data reasonable. However, the correlating ability in ascending order of various models in terms of the lowest AICc values is as follows: Bian et al., Reformulated Chrastil, Chrastil, new solid–liquid equilibrium, Mendez–Teja, RKEoS + KMmr, Alwi–Garlapati, Sodefian et al., Mahesh–Garlapati, Bartle et al., Tippana–Garlapati models. The new model proposed in this work may be useful for correlating solids solubility in any SCF.