Design of double sampling inspection plans for life tests under time censoring based on Pareto type IV distribution

Abstract

Sampling inspection plans for life tests, called reliability sampling plans, are generally employed to determine the acceptance or non-acceptance of the lot(s) of finished products by performing tests on the sampled items, measuring the lifetime of the items and observing the number of failures of items. Lifetime of individual items is a prime quality characteristic that can be treated as a continuous random variable and can be modeled by an appropriate probability distribution. In this article, double sampling plans for life tests under time censoring with a provision to draw two random samples and to admit a maximum of one failure in the combined samples are formulated assuming that the lifetime random variable follows a Pareto type IV distribution. A methodical procedure for the selection of the plan parameters using reliable life criterion with the desired discrimination protecting the interests of the producer and the consumer in terms of the acceptable reliable life and unacceptable reliable life is evolved. The operating ratio is used as a measure of discrimination in designing the proposed reliability sampling plans.

Introduction

Reliability sampling plan, also termed as life test sampling plan, is a procedure that is adopted to draw a decision on the acceptability or non-acceptability of the lot(s) of the manufactured items based on the information provided by the tests on the sampled products or items. The lifetime of the product is measured from the tests on the individual items and is considered as the prime quality characteristic as well as the continuous random variable, which is described by an appropriate probability distribution. Fertig and Mann¹ opine that a life test sampling plan is a technique for making decision on the inspected lot based on the sample(s) and employs the concept of censoring to manage the testing time at an appropriate level. In the literature of reliability sampling, four distinct censoring schemes are generally focused, viz., time censoring, failure-censoring, hybrid censoring and progressive censoring. Time censoring and failure censoring schemes are termed as time truncated and failure truncated (type I and type II) schemes. In a time terminated life test, a given sample of n items is tested until a pre-assigned termination time, t, is reached and then the test is terminated. In a failure terminated life test, a given sample size, n, is tested until the failure occurs and then the test is terminated. As type I and type II censoring schemes do not have the flexibility of allowing removal of units at points other than the terminal point of the experiment, when practical situations warrant the removal of surviving units at points other than the final termination, a progressive censoring scheme would be adopted as an alternative scheme. See, Balakrishnan and Aggarwala². The mixture of type I and type II censoring schemes is known as hybrid censoring scheme, which is considered when cost of inspection, products and product reliabilities are high.

The basic notion and theoretical development of life test sampling plans with particular reference to exponential and Weibull distributions are found in Epstein^3,4, Handbook H-108⁵, and Goode and Kao^6,7,8. The life test sampling plans based on normal and lognormal distributions have been developed by Gupta⁹. A detailed description on the construction of life test sampling plans is provided by Schilling and Neubauer¹⁰. The recent literature in the studies relating to the construction of reliability sampling plans include the works of Wu and Tsai¹¹, Wu et al.¹², Kantam et al.¹³, Tsai and Wu¹⁴, Balakrishnan et al.¹⁵, Aslam et al.¹⁶, Kalaiselvi and Vijayaraghavan¹⁷, Kalaiselvi et al.¹⁸, Loganathan et al.¹⁹, Aslam et al.²⁰, Hong et al.²¹, Vijayaraghavan et al.²², Vijayaraghavan and Uma^23,24 and Vijayaraghavan et al.^25,26.

Pareto distribution, introduced by Pareto²⁷, is a skewed and heavy-tailed distribution. It is considered as a lifetime distribution and frequently used as a model for survival-type data. One may refer to Davis and Feldstein²⁸, Wu²⁹, Hossain and Zimmer³⁰, Howlader and Hossain³¹, Wu and Chang³², Kus and Kaya³³ and Abdel-Ghaly et al.³⁴ for the details pertaining to the theory and applications of Pareto distribution. Nadarajah and Kotz³⁵ considered a class of Pareto distributions and derived the corresponding forms for applications in reliability.

Pareto distribution of the first kind (type I) is the earliest form which has drawn applications in a wide range of areas. According to Arnold³⁶, Pareto distribution of second kind (type II), also called Lomax distribution, is well adapted for modeling reliability problems as its properties are easily interpretable. Pareto distribution of third kind (type III) is considered as the generalized Pareto distribution. Arnold³⁶ defined the Pareto distribution of fourth kind (type IV) and has observed that the Pareto distributions of the first, second and third types are the particular cases of the fourth type. Singh and Maddalla³⁷ pointed out that the Pareto distribution of the fourth kind would result in decreasing failure rates. Johnson et al.³⁸ observed that the Pareto distribution of the fourth kind is related to the beta distribution of the second kind, is more flexible and has wider applicability.

Due to the possibility of decreasing failure rates, the use of Pareto distribution of the fourth kind would be much helpful for practitioners to adopt in real-life phenomena and may be used as an alternative to other heavy tailed distributions. Applications of various continuous type distributions as lifetime distributions are seen in the literature of product control, particularly in reliability sampling plans. In the following subsections, double sampling plans for life tests under time censoring with a provision to draw two random samples and to admit a maximum of one failure in the combined samples are formulated assuming that the lifetime random variable follows a Pareto type IV distribution. A methodical procedure for the selection of the plan parameters using reliable life criterion with the desired discrimination protecting the interests of the producer and the consumer in terms of the acceptable reliable life and unacceptable reliable life is evolved. The operating ratio is used as a measure of discrimination in designing the proposed reliability sampling plans.

Double sampling inspection plans for life tests

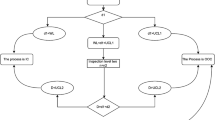
Double sampling plan (DSP) for life tests is an extension of single sampling plans and consists of a specific rule in which a second sample is drawn from the lot before it can be sentenced. It can be formulated in the following manner:

Suppose, a random sample of $n_{1}$ items is drawn from a lot and the items are placed for a life test and the experiment is stopped at a predetermined time, T. The number of failures occurred until the time point T is observed, and let it be $m_{1} .$ The lot is accepted if $m_{1}$ is equal to or less than the first acceptance number, say,$a_{1} .$ If $m_{1}$ is equal to or greater than the first rejection number $r_{1} ,$ the lot is rejected. If $a_{1} < m_{1} < r_{1} ,$ a second sample of $n_{2}$ items is taken and the number of failures,$m_{2} ,$ is observed. If the cumulative number of failures, $m_{1} + m_{2} ,$ found in the first and second samples is equal to or less than the second acceptance number,$a_{2} ,$ the lot is accepted. If $m_{1} + m_{2}$ is equal to or greater than $r_{1} ,$ the lot is rejected.

Thus, the double sampling plan for life tests is represented by the parameters $n_{1} ,\;n_{2} ,\;a_{1} ,\;r_{1}$ and $a_{2} ,$ where $n_{1}$ and $n_{2}$ are the number of items in the first and second samples, respectively, $a_{1}$ and $a_{2}$ are the allowable number of failures, called acceptance numbers, in the first sample and in the combined samples, respectively, and $r_{1} = a_{2} + 1$ is the rejection number. The plan, designated by $DSP - (n_{1} ,\;n_{2} ,\;a_{1} ,\;a_{2} ),$ is applied under the general conditions for application of sampling inspection for isolated lots.

The performance of $DSP - (n_{1} ,\;n_{2} ,\;a_{1} ,\;a_{2} )$ adopted in life testing is measured by the associated operating characteristic (OC) function, denoted by $P_{a} (p),$ which gives the probability of accepting a lot as a function of the failure probability p, and the average sample number function, denoted by $ASN(p),$ which yields the average number of items to be inspected under the plan for taking a decision about the lot. They are, respectively, expressed by

$$P_{a} (p) = F(\left. {a_{1} } \right|n_{1} ) + \sum\limits_{{m_{1} = a_{1} + 1}}^{{r_{1} - 1}} {p(\left. {m_{1} } \right|} n_{1} )F(\left. {a_{2} - m_{1} } \right|n_{2} )$$

(1)

$${\text{and}}\quad ASN(p) = n_{1} + n_{2} \sum\limits_{{m_{1} = a_{1} + 1}}^{{r_{1} - 1}} {p(\left. {m_{1} } \right|} n_{1} )$$

(2)

where $p(m|n)$ is the probability of observing m failures in a random sample of $n$ items and $F(\left. a \right|n) = \sum\nolimits_{m = 0}^{a} {p(m\,|\,n)} .$

It may be noted that under the conditions of binomial and Poisson distributions, the expressions for $p(m\,|\,n)$ are respectively given by

$$p(m|n) = \left( \begin{gathered} n \hfill \\ m \hfill \\ \end{gathered} \right)p^{m} (1 - p)^{n - m} ,\,\,\,{\text{for}}\,\,\,m = 0,\;1,\;2, \ldots ,\;n.$$

(3)

$${\text{and}}\quad p(m|n) = e^{ - np} \frac{{(np)^{m} }}{m\;!},\quad {\text{for}}\quad m = 0,\;1,\;2, \ldots .$$

(4)

Thus, the acceptance probabilities in double sampling plans under the conditions of binomial and Poisson distributions can be determined by substituting (3) and (4) in (1), respectively. In the context of life testing sampling plans, the failure probability, p, is defined by the proportion of product failing before time t, and hence, the expression for $p$ is defined by the cumulative probability distribution of T.

Double sampling plans for life tests with zero or one failure

When sampling plans for life tests are required for product characteristics that involve costly or destructive testing, and when small samples are to be involved, a sampling plan with zero or fewer failures in the samples is often employed. Dodge³⁹ observed that a single sampling plan by attributes with zero acceptance number is not desirable as it seldom protects the interests of the producer. It is demonstrated in Fig. 1 that single sampling plans for life tests with zero failures or zero acceptance number, designated by $SSP - (n,\;0),$ are not desirable as they do not provide protection to the producer against the acceptable reliable life of the product. The operating characteristic curves of such sampling plans having zero failures are uniquely in poor shape, which does not ensure protection to producers, but safeguard the interests of consumers against unacceptable reliable life of the product. It can be demonstrated that single sampling plans admitting one or more failures in a sample of items lack the undesirable characteristics of $SSP - (n,\;0),$ but require larger sample sizes. This shortcoming can be overcome, to some extent, if one follows double sampling plans with a maximum of one failure in the random samples drawn from the submitted lot.

Figure 1

Operating characteristic curves of single and double sampling plans for life tests based on Pareto type IV distribution having smaller values of acceptance numbers.

In small sample situations, single sampling plans with a fewer number of failures such as $c = 0$ and $c = 1$ can be used. But, the OC curves of $c = 0$ and $c = 1$ plans would reveal a fact that there will be a conflicting interest between the producer and the consumer as $c = 0$ plans provide protection to the consumer with lesser risk of accepting the lot having unacceptable reliable life of the product while $c = 1$ plans offer protection to the producer with lesser risk of rejecting the lot having acceptable reliable life. Such conflict can be invalidated if one is able to design a life test plan having its OC curve lying between the OC curves of $c = 0$ and $c = 1$ plans.

It can also be observed from Fig. 1 that there is a wider gap to be filled between the OC curves of $c = 0$ and $c = 1$ plans. Hence, it is, obviously, desirable to determine a plan whose OC curve is expected to lie between $c\, = \,0$ and $c\, = 1$ plans. A double sampling plan with $a_{1} = 0,\;r_{1} = 2$ and $a_{2} = 1,$ designated by $DSP - (n_{1} ,n_{2} ),$ overcomes the shortcoming of $c = 0$ plans to a greater extent by providing a desirable shape of the OC curve, which is considered as favorable to both producer and consumer. It can also be realized that the OC curves of $DSP - (n_{1} ,n_{2} )$ lie between the OC curves of $c\, = \,0$ and $c\, = 1$ plans. A special feature of $DSP - (n_{1} ,n_{2} )$ is that its OC curve coincides with the OC curve of $c\, = 1$ single sampling plan at the upper portion and coincides with the OC curve of $c\, = \,0$ single sampling plan at the lower portion. This feature would be of much help in selection of an optimum $DSP - (n_{1} ,n_{2} )$ providing protection to the producer and consumer against rejection of the lot for the specified acceptable reliable life and against acceptance of the lot for the specified unacceptable reliable life. More details about the significance and construction of sampling plans with c = 0 and c = 1 as alternative to single sampling plans with either c = 0 or with c = 1 can be had from Govindaraju⁴⁰, Soundararajan and Vijayaraghavan⁴¹ and Vijayaraghavan⁴². The operating procedure of $DSP - (n_{1} ,n_{2} )$ is as follows:

A sample of $n_{1}$ items is taken from a given lot and inspected. If no failures are found, i.e., $m_{1} = 0,$ while inspecting $n_{1}$ items, then the lot is accepted; if one failure is found, i.e., $m_{1} = 1,$ a second sample of $n_{2}$ items is taken and the number of failures, $m_{2} ,$ is observed. If no failures are found, i.e., $m_{2} = 0,$ while inspecting $n_{2}$ items, then the lot is accepted; if one or more failures are found, i.e., $m_{2}$ is greater than or equal to 1, then the lot is rejected.

Associated with $DSP - (n_{1} ,n_{2} )$ are the performance measures, called OC and ASN functions, which are, respectively, expressed by

$$P_{a} \left( p \right) = p(0|n_{1} ,p) + p(1|n_{1} ,p)p(0|n_{2} ,p)$$

(5)

and

$$ASN\left( p \right) = n_{1} + n_{2} p(0|n_{1} ,p)$$

(6)

where p is the proportion,$p,$ of product failing before time t, and $p(0|n_{1} ,p),$ $p(0|n_{2} ,p)$ and $p(1|n_{1} ,p)$ are defined either from the binomial distribution or from the Poisson distribution whose probability functions are given as expressions (3) and (4).

Pareto distribution of fourth kind

Let T be a random variable representing the lifetime of the components. Assume that T follows a Pareto distribution of fourth kind, named as Pareto Type IV distribution. The probability density function and the cumulative distribution function of T are, respectively, defined by

$$f(t;\delta ,\theta ,\eta ,\lambda ) = \frac{\lambda }{\eta \theta }\left( {1 + \left( {\frac{t - \delta }{\theta }} \right)^{{\frac{1}{\eta }}} } \right)^{ - (\lambda + 1)} \left( {\frac{t - \delta }{\theta }} \right)^{{\frac{1}{\eta }\; - \;1}} ,\;t > \delta ,\;\theta ,\eta ,\lambda > 0$$

(7)

$${\text{and}}\quad F\left( {t;\delta ,\theta ,\eta ,\lambda } \right) = 1 - \left( {1 + \left( {\frac{t - \delta }{\theta }} \right)^{{\frac{1}{\eta }}} } \right)^{ - \lambda } ,\;t > \delta ;\theta ,\eta ,\lambda > 0$$

(8)

where $\delta$ is the location parameter, $\theta$ is the scale parameter, $\lambda$ is the shape parameter and $\eta$ the inequality parameter. When $\delta = 0$, (7) and (8) would become

$$f(t;\delta ,\theta ,\eta ,\lambda ) = \frac{\lambda }{\eta \theta }\left( {1 + \left( {\frac{t}{\theta }} \right)^{{\frac{1}{\eta }}} } \right)^{ - (\lambda + 1)} \left( {\frac{t}{\theta }} \right)^{{\frac{1}{\eta }\; - \;1}} ,\;t > 0,\;\theta ,\eta ,\lambda > 0$$

(9)

$${\text{and}}\quad F\left( {t;\theta ,\eta ,\lambda } \right) = 1 - \left( {1 + \left( {\frac{t}{\theta }} \right)^{{\frac{1}{\eta }}} } \right)^{ - \lambda } ,\;t > 0;\theta ,\eta ,\lambda > 0$$

(10)

The mean life, reliability function and the hazard rate for a specified time t under the Pareto distribution are, respectively, given by

$$\mu = \theta \frac{\Gamma (\eta + 1)\Gamma (\lambda - \eta )}{{\Gamma (\lambda )}},$$

(11)

$$R(t) = \left( {1 + \left( {\frac{t}{\theta }} \right)^{{\frac{1}{\eta }}} } \right)^{ - \lambda }$$

and

$$Z\left( t \right) = \frac{\lambda }{\eta \theta }\left( {1 + \left( {\frac{t}{\theta }} \right)^{{\frac{1}{\eta }}} } \right)^{ - 1} \left( {\frac{t}{\theta }} \right)^{{\frac{1}{\eta } - 1}}$$

(12)

where $\Gamma$ is the Gamma Function.

The reliable life is the life beyond which some specified proportion of items in the lot will survive. The reliable life associated with Pareto distribution is defined and denoted by

$$\rho = \theta \left( {R(t)^{{ - \frac{1}{\lambda }}} - 1} \right)^{\eta }$$

(13)

The proportion,$p,$ of product failing before time t, is defined by the cumulative probability distribution of T and is expressed by

$$p = P(T \le t) = F(t;\theta ,\eta ,\lambda )$$

(14)

The performance of $DSP - (n_{1} ,n_{2} )$ for life tests is measured by the associated OC function, denoted by $P_{a} (p),$ which gives the probability of accepting a lot as a function of the failure probability p. Under the conditions for the application of binomial and Poisson models, the expressions for $P_{a} (p)$ from (1) using (3) and (4) are, respectively, given by

$$P_{a} \left( p \right) = (1 - p)^{{n_{1} }} + n_{1} p(1 - p)^{{n_{1} + n_{2} - 1}}$$

(15)

and

$$P_{a} \left( p \right) = e^{{ - n_{1} p}} + n_{1} pe^{{ - (n_{1} + n_{2} )p}}$$

(16)

Defense Department Quality Control and Reliability Technical Report TR6⁴³ proposed the reliable life criterion as one of the three reliability criteria for designing reliability sampling plans when Weibull distribution is the underlying distribution for a lifetime random variable. It used the dimensionless ratio t / ρ which is related to the cumulative probability p, which is the proportion of product failing before time t. Analogous to this case of t/ρ for Weibull distribution, double sampling plans with zero or one failure indexed by the reliable life giving protection to the producer and consumer are now determined.

Search procedure for the selection of $DSP - (n_{1} ,n_{2} )$

In reliability sampling, a specific sampling plan for life tests can be obtained by specifying the requirements that its operating characteristic (OC) curve should pass through two points, namely, $(\rho_{0} ,\alpha )$ and $(\rho_{1} ,\beta ),$ where $\rho_{0}$ and $\rho_{1}$ are the acceptable and unacceptable reliable life, associated with the risks $\alpha$ and $\beta ,$ respectively. The quantities $\rho_{0}$ and $\rho_{1}$ in reliability sampling are the counterparts of the lot quality levels in acceptance sampling, and hence, the operating ratio,$OR = \rho_{0} /\rho_{1}$, which is the ratio of acceptable reliable life to unacceptable reliable life, can be used as the measure of discrimination just similar to the operating ratio of the limiting quality level to the acceptable quality level in acceptance sampling. An optimum double sampling plan for life tests can be obtained by satisfying the following two conditions with the fixed value of producer's and consumer's risks at α and β, respectively, with minimum ASN:

$$P_{a} (\rho_{0} ) \ge 1 - \alpha$$

(17)

$${\text{and}}\quad P_{a} (\rho_{1} ) \le \beta .$$

(18)

It may be noted that the OC function is a function of t / ρ, which corresponds to the cumulative distribution, p, i.e., the proportion of lot failing before time t. Hence, for specified values of $t/\rho_{0}$ and $t/\rho_{1}$, the optimum values of $n_{1}$ and $n_{2}$ of $DSP - (n_{1} ,n_{2} )$ for the specified requirements under the conditions of Pareto type IV distribution can be determined by using the following procedure:

• Step 1: Specify the value of the shape parameters $(\lambda ,\eta )$ or their estimates.

• Step 2: Specify the proportion, r, of the items that will survive in the population beyond the reliability life, ρ.

• Step 3: Specify the values of $t/\rho_{0}$ and $t/\rho_{1}$, with the associated risks $\alpha = 0.05$ and $\beta = 0.10,$ respectively, so that the operating ratio is defined by $OR = \rho_{0} /\rho_{1}$ and $t/\rho_{0}$.

• Step 4: Using the relationship between p and ρ, from (13) and (14), obtain $p_{0}$ and $p_{1}$ corresponding to $t/\rho_{0}$ and $t/\rho_{1}$.

• Step 5: Search for the values of $n_{1}$ and $n_{2}$ for the specified strength $(\rho_{0} ,\;1 - \alpha )\;$ and $(\rho_{1} ,\;\beta )$ with the values of $p_{0}$ and $p_{1}$ satisfying the conditions (17) and (18), by using the expression (15) or (16).

Based on the above procedure, fixing the value of r as 90%, the optimum double sampling plans for life tests under the assumption of Pareto type IV distribution are obtained for a set of values of $(\lambda ,\eta )$ such as (1, 0.5), (2, 0.5), (2, 0.6) and (2, 0.7), and for various combinations of $OR = \rho_{0} /\rho_{1}$ and $t/\rho_{0}$. These plans are provided in Tables 1, 2, 3 and 4 along with the values of minimum ASN at $t/\rho_{0}$.

Table 1 Optimum $DSP - (n{}_{1},n_{2} )$ for life tests based on Pareto type IV distribution having shape parameters $\lambda = 1$ and $\eta = 0.5$ (r = 0.90). Key: $n{}_{1},n_{2} ,ASN\;at\;p_{1}$.

Table 2 Optimum $DSP - (n{}_{1},n_{2} )$ for life tests based on Pareto type IV distribution having shape parameters $\lambda = 2$ and $\eta = 0.5$(r = 0.90). Key: $n{}_{1},n_{2} ,ASN\;at\;p_{1}$.

Table 3 Optimum $DSP - (n{}_{1},n_{2} )$ for life tests based on Pareto type IV distribution having shape parameters $\lambda = 2$ and $\eta = 0.6$ (r = 0.90). Key: $n{}_{1},n_{2} ,ASN\;at\;p_{1}$.

Table 4 Optimum $DSP - (n{}_{1},n_{2} )$ for life tests based on Pareto type IV distribution having shape parameters $\lambda = 2$ and $\eta = 0.7$(r = 0.90). Key: $n{}_{1},n_{2} ,ASN\;at\;p_{1}$.

Procedure for the selection of DSP−(n₁, n₂) using the tables

The parameters of a double sampling plan for life tests when the lifetime random variables follows a Pareto type IV distribution are chosen from the given tables by the following method:

• Step 1: Specify the values of $\lambda$ and $\eta$ or their estimates based on a past history.

• Step 2: Specify the test termination time, t, and the requirements $(\rho_{0} ,\;1 - \alpha )\;$ and $(\rho_{1} ,\;\beta )$.

• Step 3: Compute $t/\rho_{0}$ and $t/\rho_{1}$ with $\alpha = 0.05$ and $\beta = 0.10,$ respectively.

• Step 4: Find the operating ratio, $OR = \rho_{0} /\rho_{1}$.

• Step 5: Enter the appropriate table (among Tables 1, 2, 3 and 4) corresponding to the given set of values of $\lambda$ and $\eta ;$ choose the values of $n_{1}$ and $n_{2}$ corresponding to the value of $t/\rho_{0}$ and the operating ratio which is just closer to OR found in Step 3.

Thus, the values of $n_{1}$ and $n_{2}$ will constitute the required optimum $DSP - (n_{1} ,n_{2} )$ for life tests satisfying the given requirements. The optimum plan would admit a maximum of one failure in an accepted lot.

Numerical illustration 1

A double sampling plan for life tests is to be instituted when the lifetime of the component is considered as a random variable which follows a Pareto type IV distribution whose shape parameters are specified as $\lambda = 1$ and $\eta = 0.5$. Assume that nearly 90% of items in the population will survive beyond the reliability life ρ, i.e., r = 0.90. It is expected that interests of the producer and the consumer are to be protected when the acceptable reliable life and the unacceptable reliable life are specified $\rho_{0} = 2500$ hours and $\rho_{1} = 500$ hours, respectively, with the associated producer’s risk of 5% and consumer’s risk of 10%.

It is desired that the life test is to be terminated at t = 200 h. From the given set of values, one finds OR = 5 and $t/\rho_{0} = 0.08$. Thus, entering Table 1 with $OR = \rho_{0} /\rho_{1} = 5$ and $t/\rho_{0} = 0.08$, the optimum double sampling plan is chosen having its sample sizes $n_{1} = 131$ and $n_{2} = 340,$ which yield $ASN = 160.$ One may obtain acceptable and unacceptable quality levels corresponding to $\rho_{0} = 2500$ hours and $\rho_{1} = 500$ hours using the relationship between t / ρ and p as 0.000711 and 0.017467, respectively. Thus, the desired plan for the given conditions is implemented as given below:

• 1. Choose $n_{1} = 131$ items from a lot.

• 2. Conduct the life test experiment on each sampled item.

• 3. Count the number of failures, x, before attaining the termination time.

• 4. Terminate the life test at time $t = 200$ hours.

• 5. If no failures are observed in the 131 items tested or until time t is reached, accept the lot; if there are 2 or more failures, reject the lot; if one failure is observed, select a random sample of $n_{2} = 340$ items.

• 6. Conduct the life test on each of the 340 items. Accept the lot, when there are no failures in the 340 items; if one or more failures are observed, reject the lot.

• 7. Treat the items which survive beyond time $t = 200$ hours as passed.

Numerical illustration 2

Consider a situation in which the lifetime of an item follows the Pareto type IV distribution which has the shape parameters $\lambda$ and $\eta .$ Assume that the estimated values of $\lambda$ and $\eta$ are 2 and 0.5, respectively. The life test will be terminated at t = 500 h. The acceptable and unacceptable proportion of failures are prescribed as $p_{0} = 0.168\%$ and $p_{1} = 2.65\%$ with the associated producer’s and consumer’s risks specified as $\alpha = 0.05$ and $\beta = 0.10$. Corresponding to $p_{0} = 0.168\%$ and $p_{1} = 2.65\%$, one obtains $t/\rho_{0} = 0.125$ and $t/\rho_{1} = 0.5$. Hence, the desired operating ratio is obtained as $OR = \rho_{0} /\rho_{1} = 4.$ As $\lambda = 2$ and $\eta = 0.5,$ entering Table 2, the optimum double sampling plan is identified with its samples sizes given as $n_{1} = 86$ and $n_{2} = 213$ yielding ASN = 113 at $t/\rho_{0} = 0.125$. The desired sampling plan satisfies the conditions the conditions (17) and (18). The acceptable and unacceptable reliable life, corresponding to $p_{0} = 0.168\%$ and $p_{1} = 2.65\%$ are determined, $\rho_{0} = {t \mathord{\left/ {\vphantom {t {0.125}}} \right. \kern-\nulldelimiterspace} {0.125}} = 4000$ h and $\rho_{1} = {t \mathord{\left/ {\vphantom {t {0.5 = }}} \right. \kern-\nulldelimiterspace} {0.5 = }}1000$ h, respectively.

Figures 2 and 3 display the OC curves of the double sampling plans obtained in Numerical Illustrations 1 and 2. It can be observed in Fig. 2 that the OC curve of the double sampling plan $(n_{1} = 131,n_{2} = 340)$ for life tests based on the Pareto type IV distribution passes through the desired points, namely, (0.08, 0.9777) and (0.4, 0.0999). Similarly, from Fig. 3, it can be noted that the optimum plan $(n_{1} = 86,n_{2} = 213)$ passes through the points (0.125. 0.9525) and (0.5, 0.09998).

Figure 2

OC curves of double sampling plans for life tests based on Pareto type IV distribution with $n_{1} = 131,n_{2} = 340,\lambda = 1$ and $\eta = 0.5$.

Figure 3

OC curves of double sampling plans for life tests based on Pareto type IV distribution with $n_{1} = 86,n_{2} = 213,\lambda = 2$ and $\eta = 0.5$.

Numerical illustration 3

A manufacturing industry produces various models of rotating wheels which can be used for different applications. The quality levels of rotating wheels are specified in terms of the useful life which is measured in terms of the expected number of revolutions per minute. For a particular make of rotating wheel, the producer specifies that, nearly 90% or more of the items would survive beyond 1000 revolutions per minute and expects that the lot should have the probability of acceptance at 0.95, i.e., $(\rho_{0} = 1000,\alpha = 0.05)$. The consumer’s specification is that 90% or more of the items will survive 118 or lesser revolutions per minute, i.e., and 10% risk of accepting such a lot, $(\rho_{1} = 118,\;\beta = 0.10).$

From the history, it was ascertained that the quality variable of rotating wheel follows a Pareto type IV distribution with parameters $\lambda$ and $\eta$, specified 2 and 0.7. For the given situation, it is desired to institute a reliability double sampling plan. It is assumed that the life test is to be performed on rotating wheels until reaching $t = 100$ revolutions per minute (rpm) at its axis. The tested rotating wheel when it does not reach 100 revolutions per minute can be treated as a failure of the item. From the given requirements the values of $t/\rho_{0}$ and $t/\rho_{1}$ are obtained as $t/\rho_{0} = 0.1$ and $t/\rho_{1} = 0.85.$ The operating ratio is found as $OR = \rho_{0} /\rho_{1} = 8.5$. As $\lambda = 2$ and $\eta = 0.7,$ by entering Table 4 with $OR = \rho_{0} /\rho_{1} = 8.5$ and $t/\rho_{0} = 0.1$, the optimum parameters of the double sampling plan are chosen as $n_{1} = 28$ and $n_{2} = 47,$ with the associated ASN = 33 at $t/\rho_{0} = 0.1$. Thus, the desired plan is implemented is as follows:

Select a first random sample of $n_{1} = 28$ rotating wheels and conduct the life test on each of the selected item; if no failures are observed until reaching t = 100 revolutions per minute, accept the lot; if one failure is observed, select a second random sample of $n_{2} = 47$ items. Conduct the life test on each of the 47 items. Accept the lot, when there are no failures in the 47 items; if one or more failures are observed, reject the lot.

Simulation study

A simulation study is carried out for comparing the results arrived in the above illustration. The simulated results are based on 10,000 runs using R programming. Initially, first random sample of size $n_{1} = 28$ is simulated from Pareto type IV distributions with the shape parameters $\lambda$ and $\eta$ are specified 2 and 0.7. The resulted simulated data are arranged in an ascending order as given below: 98.79, 100.25, 101.24, 102.25, 103.11, 104.30, 106.13, 111.38, 111.52, 113.28, 115.61, 124.66, 127.65, 130.24, 132.01, 135.11, 137.00, 139.22, 140.31, 140.54, 141.32, 146.71, 153.96, 155.49, 159.07, 180.52, 254.41, 275.76.

It can be observed that there is one failure before truncation of $t = 100$ revolutions, hence, a second random sample of $n_{2} = 47$ observations is generated from the distribution having the parameters $\lambda$ and $\eta$ specified as 2 and 0.7, respectively. The simulated data are given below in the ascending order:

101.09, 102.20, 104.79, 106.60, 107.80, 108.79, 109.05, 109.08, 109.64, 111.00, 111.30, 113.23, 113.86, 115.32, 116.56, 117.21, 117.62, 117.99, 121.55, 121.90, 122.47, 125.69, 126.87, 126.97,127.27, 131.32, 135.52, 138.34, 139.34, 142.19, 142.47, 142.89, 143.32, 143.34, 147.79, 149.53, 154.73, 155.55, 159.25, 166.36, 170.70, 180.66, 205.85, 207.36, 242.14, 269.06, 310.49.

It can be noted that the entities in the simulated data exhibit the more than t = 100 and no failure is observed in the second sample. Hence, the lot is treated as accepted.

Conclusion

Double sampling plans for life tests are proposed when the lifetime random variable follows a Pareto type IV distribution. A procedure for designing the sampling plans indexed by acceptable and unacceptable reliable life for a situation involving time truncation is discussed with illustrations. Tables yielding optimum double sampling plans for life tests for a selected set of parametric values of Pareto type IV distribution. A simulation study has been carried out to demonstrate the application of the proposed plans for the industrial needs.