Abstract
Control theory has seen recently impactful applications in network science, especially in connections with applications in network medicine. A key topic of research is that of finding minimal external interventions that offer control over the dynamics of a given network, a problem known as network controllability. We propose in this article a new solution for this problem based on genetic algorithms. We tailor our solution for applications in computational drug repurposing, seeking to maximize its use of FDA-approved drug targets in a given disease-specific protein-protein interaction network. We demonstrate our algorithm on several cancer networks and on several random networks with their edges distributed according to the Erdős–Rényi, the Scale-Free, and the Small World properties. Overall, we show that our new algorithm is more efficient in identifying relevant drug targets in a disease network, advancing the computational solutions needed for new therapeutic and drug repurposing approaches.
Similar content being viewed by others
Introduction
Network modeling in systems medicine has emerged as a powerful analytics approach in the last couple of decades1,2. Its aim is to analyze diseases and drug interventions as ways of acting over bio-medical dynamical networks3,4, such as protein-protein interaction networks5,6, signalling networks7, metabolic networks8, and immunological responses9. In this framework, a disease is seen as emerging from some of its modules being affected (directly or through cascading signals) and from critical nodes in the network being deregulated10. Similarly, drug therapies are seen as outside controlled interventions within a deregulated network with the aim of either re-balancing the system or possibly isolating some specific components of the network11. A particular advantage of this approach is reasoning about multiple-drug interventions, analyzing and predicting multi-drug synergies. Instead of acting over each individual dysregulated component, one can try to influence several of these entities through a few well-chosen interventions, and to have them spread in cascade into the network using the network’s own internal connections. Network controllability is a topic of high relevance in this area with a rich theory to support it12. It has found in recent years powerful applications in computational systems medicine and therapeutics5,6,13,14.
The theory of network controllability aims at providing a sound and theoretically accurate description of what control means within a network, and how it can be achieved. Intuitively, achieving control over a system from a set of input nodes means being able to drive that system from any initial setup to any desired state. This is an intrinsic global optimization problem with the objective to minimize the number of input nodes needed for the control. Additional constraints may be added depending on the application, such as the control pathways from the input nodes to the controlled nodes to be short, or the input nodes to be primarily selected from a given set of preferred nodes (e.g., targets of standard therapy drugs). This leads to several problem variations, such as: structural controllability13 (identifying pathways that offer control over the system regardless of its numerical setup); target controllability14 (achieving control over a predefined set of target nodes); constrained target controllability15 (selecting the input nodes from a pre-defined preferred set); target controllability with minimal mediators16 (avoiding specific nodes that could cause side-effects); minimum dominating sets17 (finding a minimal set of nodes that are one step upstream of all other nodes in the network). Some of these optimization problems are known to have efficient algorithmic solutions13. Others, on the contrary, are known to be computationally difficult, yet approximate efficient solutions are still achievable5. Recent successful applications of network controllability include research on the contribution of individual neurons in the locomotion of C. elegans18, and on the discovery of potential drug combinations for leukemia19, breast cancer and COVID-1920.
Motivated by the applicability of network control in systems medicine, the problem we focus on in this paper is minimizing the number of external interventions needed to achieve structural target control of a system. We are particularly interested in the case where the targets are disease-specific survivability-essential genes, key targets for synthetic lethality21. We identify control interventions that are achievable through the delivery of FDA-approved drugs, by giving a preference to FDA-approved drug targets being selected as input nodes. The minimization of the number of input nodes is part of the standard optimization objective of the network controllability problem and there is an additional incentive to minimize them in the medical case studies: combinatorial drug therapies can only include few simultaneously delivered drugs. The optimization goal of the network controllability problem can address this constraint by selecting the input nodes among the drug-approved nodes.
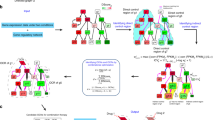
The structural target controllability problem is known to be NP-hard5, meaning that finding the smallest set of inputs for controlling the target set is computationally prohibitive for large networks. Several greedy-based approximations of the optimal solutions have been proposed for different variants of the problem5,14,15,16, also recent solutions based on linear integer programming20. In our experience6,22, the greedy algorithm tends to select few preferred input nodes in each solution. This is understandable since its search is based on consecutive edge selections that may lead it away from the preferred input nodes. To address this problem, we propose a new solution based on genetic algorithms, a well known heuristic choice for nonlinear optimization problems23. This offers a different approach to searching for a solution to network controllability: the search is on suitable combinations of input nodes that control the set of target nodes. We maximize the use of the preferred input nodes in each step of the algorithm, to get a considerably larger selection of such nodes in the solution. An overview of the basic outline of the genetic algorithm is presented in Fig. 1 and discussed in details in the “Methods” section.
The basic outline of the genetic algorithm, shown in a clockwise manner: the required data, the initial setup and chromosome encoding, the operators of the genetic algorithm, and the chromosome decoding and final result. In brief, the algorithm starts with an initialization stage, where it generates a “population” of control sets for the target set; the controllability is verified through the Kalman rank condition12. It then attempts to generate control sets of smaller and smaller size through combinations of the current control sets (crossover and mutation) and through adding new control sets to the population of solutions.
Drug repurposing, i.e., identifying novel uses for already existing drugs, has received significant attention due to its potential for efficient advances in drug development, leading to a significantly shorter timeline and reduced costs24. In addition to the standard experimental approach, recent advances in computational methods and the availability of high-quality big data enabled the evolution of efficient and promising computational approaches. Moreover, the urgency of the current COVID-19 pandemic has brought additional interest in the potential of computational drug repurposing22,25,26. Multiple computational methods have been successfully applied to the identification of drug repurposing candidates: machine learning (neural networks27, deep learning28, support vector machines and random forests29), data mining (text mining30, semantic inference31), and network analysis (clustering32, centrality measures33, controllability26). Our method can be placed at the intersection of AI- and network-based computational drug repurposing approaches, using evolutionary algorithms rooted in the structure of interaction networks and integrating additional disease- and drug-data.
Results
We tested the genetic algorithm on 15 random directed networks, generated using the NetworkX Python package34, with the number of nodes ranging from 100 to 2000 and the edges distributed according to the Erdős–Rényi-, the Scale-Free-, and the Small World-graph edge distributions. For each network, the target sets consisted of \(5\%\) randomly selected nodes with positive in-degree (which gives them a chance to be controlled). Furthermore, as a proof-of-concept, we applied the algorithm on 9 breast, pancreatic, and ovarian cancer cell line-specific directed protein–protein interaction networks6,35. These networks were constructed based on protein data from the UniProtKB database36 and interaction data from the SIGNOR database37. We used as control targets the cancer-essential genes specific to each cell line35, and as preferred control inputs the FDA-approved drug-targets of DrugBank38. An overview of the networks is presented in Table 1 (the number of nodes, edges, preferred nodes, and target nodes), in Supplementary Fig. S1 (the out-degree centrality, the closeness centrality, and the betweenness centrality), and in Supplementary Table 1.
The approach we took in this study is based on unlabelled directed networks, i.e., where we only include the information that a certain directed interaction between two proteins exists, without the details on the nature (e.g., inhibiting or activating) or the strength of that interaction. This is indeed the most common approach to network controllability. Skipping the labelling of the interactions may lead to some false positive results regarding the therapeutic effects: some of the control pathways we identify may have a weak result due to the conflicting contributions of the interactions it consists of. A modest amount of false positives is sometimes tolerated in medical research, more than false negatives, because it leads to a wider pool of candidates to be verified experimentally. Approaches representing the type of interaction within the network and within the controllability problem do exist, e.g., based on Boolean networks39,40, but they are hindered by major scalability problems.
We compared the results of the genetic algorithm to the results of the greedy algorithm for structural target controllability described in5,6. The greedy approach (the algorithm description is in the “Supplementary Information”) to structural constrained target controllability is to build control paths ending in the target nodes and starting in a minimal set of input nodes. The algorithm involves solving an iterated maximum matching problem, based on a graph theoretical result of41. The algorithm starts from the target nodes and constructs the control paths by elongating them against the direction of the edges, seeking to minimize the number of new nodes added to the paths in each step. The nodes that can eventually be no longer matched become the input nodes and they are offered as a solution to the structural target controllability problem. The focus of the algorithm is on constructing the control paths connecting the inputs to the targets, and their objective is to minimize the number of input nodes, at the cost of arbitrarily long control paths from the input nodes to the target nodes. In contrast, the genetic algorithm focuses on identifying combinations of nodes in the network that offer a solution to the structural target control problem being solved. It does this in two stages. In the initial stage, a number of solutions are generated by selecting one node from the predecessors of each of the target nodes. To check that such a selection is a solution to the structural target control problem, we use the Kalman rank condition12. The search is done within a set distance upstream of the target nodes, to constrain the search space (and implicitly, to constrain the length of the control paths). Any selection of nodes that fails the Kalman rank condition is discarded. In the second stage, the new solutions are generated through combinations of the current solutions and through adding new random solutions to the population. Each new solution is verified for consistency with the Kalman rank condition and discarded if it fails it. Several solutions are also discarded in each step: those with the highest number of input nodes. The size of the population being maintained in the search is a parameter to be set by the modeler; in our tests we used populations of 80 solutions in each iteration of the genetic algorithm. The search strategy of the genetic algorithm is discussed in detail in the “Supplementary Information”.
The greedy algorithm offers a single solution per run, while the genetic algorithm offers several solutions per run: those of minimal size in the population of solutions of the last step of its search. To make the comparison between the greedy and the genetic algorithms balanced, we defined an iteration of the greedy algorithm as a set of 80 independent runs, offering a total of 80 solutions per iteration. Also, to investigate the effect of the pathways being constrained to a certain maximum length (as done in the genetic algorithm), we ran the greedy algorithm in two different settings. In one variant, the maximum path length of the control path was bounded by the same parameter as the genetic algorithm (5, 15, 30, and 50 in different tests, details below). In the other variant, the maximum path length was left unconstrained. Each of the three algorithms (genetic, constrained greedy and unconstrained greedy) was run in this setup 10 times. All the data and the results are available in Supplementary Table 2, and in the application repository at42.
Minimizing the number of input nodes
A first benchmark objective that we compared against was the number of distinct solutions identified by each run of the algorithms (repeated runs for greedy, as explained above), and their sizes (number of input nodes). We experimented with different values for the maximum path length (5, 15, 30, and 50), to test the scalability of the methods and the influence of the longer control paths on the size of the solutions. The results are discussed below and presented in detail in Fig. 2A1–C3, and in Supplementary Table 2.
The results of the algorithms on the random networks. For all colors, the darker the shades, the longer are the maximum allowed control paths. (A) The number of the identified solutions, (B) the size of the solutions, (C) the length of the control paths in the solutions, (D) running time. Column 1: the Erdős–Rényi networks, column 2: the Scale-Free networks, column 3: the Small World networks. In blue: the results of the genetic algorithm, in green: the results of the constrained greedy algorithm, in orange: the results of the unconstrained greedy algorithm; from left to right, all plots: the networks with 100/500/1000/1500/2000 nodes.
Regarding the number of solutions, (Fig. 2A1–A3) the genetic algorithm identified more solutions than the greedy algorithms in most cases, up to 20 times more in some cases. There were only a few exceptions: in the case of Erdős–Rényi networks with 1500 and with 2000 nodes, the genetic algorithm identified roughly the same number of solutions as the unconstrained greedy, and several times more than constrained greedy. Also, the comparison was inconclusive in the case of the smallest random networks, with only 100 nodes. Obtaining more solutions is a key advantage of the genetic algorithm, especially for large drug repurposing applications, where multiple alternative solutions are important to collect and compare.
Regarding the size of the solutions, (Fig. 2B1–B3) compared to the constrained greedy algorithm, the genetic algorithm identified, on average, solutions 20–50% smaller for the Erdős–Rényi networks, and 50–70% smaller for the Small World networks, for all maximum path length values we experimented with. The differences are minor for the smaller networks, regardless of the allowed maximum path length, but become increasingly notable for the larger networks. The unconstrained greedy algorithm found smaller solutions than the genetic algorithm in the case of the Erdős–Rényi networks and of the Small World networks, at the cost of control paths up to \(500\%\) longer, (Fig. 2C1–C3). This is not surprising, because the size of the solutions is closely related to the length of the control paths: the longer the control path, the more targets a single input node can control, so the fewer input nodes are needed to control all targets. When we increased the maximum allowed length of the control paths in the genetic algorithm, the size of its solutions became comparable to that of the unconstrained greedy algorithm. In the case of the Scale-Free networks, the three algorithms identified solutions of roughly the same size. This is because these networks tend to have a small diameter and so, long paths do not exist, eliminating the key advantage of the unconstrained greedy algorithm.
Running times and convergence speed
Another benchmark objective that we investigated was the total running time and the speed of convergence to a minimal solution. The results are discussed below and presented in detail in Fig. 2D1–D3, and in Supplementary Table 2.
The genetic algorithm had a comparable running time to the constrained greedy algorithm, from 2 times slower to 2 times faster, and was up to 500 times faster than the unconstrained greedy algorithm for the Erdős–Rényi and Small World networks. On the other hand, in the case of the sparser-connected Scale-Free network, the greedy algorithms were considerably faster than the genetic one. The reason for the greedy algorithm being faster on these networks is that fewer edges implies fewer options to test when building the control paths, hence a faster running time. The Scale-Free networks tend to have a small number of “hubs” (highly connected nodes) and this leads to a difficulty with the genetic algorithm: such hubs may be considered as potential control inputs for many targets (because of their high number of descendants in the networks), but the Kalman condition will fail anytime they are suggested as control inputs for two or more targets at the same distance from the hub.
We analyzed the evolution of the quality of the solutions throughout the ten iterations of each of the algorithms, and we noticed that the optimal solutions were found very quickly, typically within the first three iterations. Moreover, within one iteration of the genetic algorithm, a near-optimal solution (i.e., a solution with the size within \(10\%\) of the best solution) was achieved very quickly, typically within 80 generations from the start for the Erdős–Rényi and Small World networks, and within only ten generations for the Scale-Free networks (Fig. S2). This suggests that the genetic algorithm may be applied successfully with a much lower number of generations, adding a considerable speed-up to it; by default, in our study we used a default number of 100 consecutive generations without an improvement in the size of the optimal solutions.
Maximizing the use of preferred inputs
We compared the ability of the three algorithms to maximize the use of preferred nodes, and we performed a brief literature-based validation of the relevance of the drug-targets and drugs found for the cancer networks. The results are discussed below and presented in detail in Fig. 3, and in Supplementary Table 2.
The results of the algorithms on the biological networks. (A) Number of identified drug-targetable inputs, (B) number of targets controllable from the identified drug-targetable inputs; column 1: breast cancer networks, column 2: ovarian cancer networks, column 3: pancreatic cancer networks; in blue: (constrained) genetic algorithm, in green: constrained greedy algorithm, in orange: unconstrained greedy algorithm.
We applied the three algorithms on our benchmark biological networks with the additional optimization objective of maximizing the selection of FDA-approved drug targets as preferred input nodes. In the greedy algorithm, maximizing the use of FDA-approved drug targets is implemented in every step of extending the control paths. All nodes acting as starting points in the control paths being constructed are attempted to be matched with preferred nodes; the nodes left unmatched are then attempted to be matched with un-preferred nodes; finally, the nodes that could not be matched towards longer control paths are selected as input nodes and their control path is completed. In the genetic algorithm, maximizing the use of preferred nodes is done when selecting the potential input nodes in every candidate solution. The choice is stochastic with a larger probability to be selected set for the preferred nodes. In our experiments we used a probability of 2/3 for the preferred nodes to be selected in a candidate solution and a probability of 1/3 for the un-preferred nodes. The optimal balance between the two probabilities is a function of the balance between preferred and un-preferred nodes in the network, and of their out-degrees. Too high a probability for preferred nodes may make it difficult to get a full rank controllability matrix (i.e., to control the entire target set) and many attempts may have to be made before one is found; too low a probability for them will lead to a sub-optimal solution in terms of how many preferred nodes are eventually included in the optimal solution.
For all networks and for all experiments we ran, the sets of input nodes returned by the genetic algorithm contained, on average, 150–300% more preferred nodes than the ones returned by either of the greedy algorithms. This led to 120–320% more control target nodes being controlled by preferred nodes in all but one cases, i.e., leading to predictions of potentially more efficient drugs. This has as a consequence a clear improvement in the applicability of the algorithm in the biomedical domain for drug repurposing, an aspect that we discuss in the next subsection.
To test the reproducibility of the results and the robustness of the genetic algorithm, we investigated how often the preferred nodes are identified over multiple runs of the algorithm. We performed these tests within two setups. First, we ran the algorithm 10 times on the benchmark biological networks; with the algorithm being stochastic, there was a diversity of solutions offered from run to run. Second, we ran the algorithm 10 times more, each time on slightly modified networks, with a random set of \(5\%\) edges removed for each iteration, to emulate the effect of false positives in the interaction data. The results are presented in Fig. 4. In both cases, about \(50\%\) of the preferred nodes were consistently identified in at least 7 of the 10 runs, and about \(30\%\) were identified in at least 9 of the 10 runs.
The distribution of input nodes repeatedly identified over 10 iterations of the genetic algorithm for the biological networks. For each biological network we counted how many of the input nodes were found in at least 9–10/7–8/5–6/3–4/1–2 of the 10 runs we did on that network. The box plots show the distribution of these counts over all the biological networks. (A) Repeated (stochastic) runs over the biological networks. (B) Repeated runs over the biological networks with of their \(5\%\) edges randomly removed.
Therapeutically relevant results
We performed a brief analysis of the top FDA-approved drug targets identified in multiple runs of the algorithms for each of the biological networks. We used the DrugBank database38 to find approved and investigational drugs targeting these proteins and known to be used in cancer therapeutics. To avoid spurious selections of inputs, for each cancer type, we considered only the drug targets that have been identified in at least half of the runs of one of the three algorithms. The sets of drug-targets returned by the unconstrained and constrained versions of the greedy algorithms and their corresponding drugs have been combined for a better comparison against the genetic algorithm. Even so, for all the cancer networks we analyzed, the genetic algorithm managed to identify more than twice drug-targets and cancer-related drugs than its counterparts. With only one exception, all of these drug-targets are known to be of significance in the corresponding cancer type. The results are presented in Table 2, in Fig. 5, and in Supplementary Table 3.
The identified drug-targets over repeated iterations for each algorithm. (A) Considering the drug-targets identified in at least one iteration by at least one algorithm, (B) considering the drug-targets identified in at least half of the iterations by at least one algorithm; column 1: specific-algorithm identified drug-targets, column 2: overlap between identified drug-targets by algorithm; in blue: (constrained) genetic algorithm, in green: constrained greedy algorithm, in orange: unconstrained greedy algorithm, in yellow: the intersection of all algorithms.
Out of the nine top preferred inputs identified solely by the genetic algorithm for the breast cancer networks, eight are known to be of significance in breast cancer proliferation: VDAC143, DDR144, ALK45, SRC46, JAK247, FGFR448, LCK50, and FGF451. In addition, there are six more preferred inputs identified by both the genetic and by the greedy algorithms, out of which five are known as important in breast cancer: KEAP180, PIM181, DDR283, RET84, and EGFR85. Furthermore, the remaining two top preferred inputs are known to be of significance in other cancer types: IL3RA49 and IL382, marking them as potential drug repurposing targets for future research. The greedy algorithms returned only two specific preferred inputs not found by the genetic algorithm, both known to be significant for breast cancer: IGF1R73 and AKT174. We found fourteen cancer-related drugs which are targeting inputs only identified by the genetic algorithm, four of which have been investigated for the treatment of breast cancer (crizotinib57, dasatinib59, lenvatinib65, and nintedanib68), and ten drugs used in an active or in a completed clinical trial (alectinib52, bosutinib54, crizotinib58, dasatinib60, entrectinib52, infigratinib63, lenvatinib66, nintedanib69, pemigatinib52, and ponatinib52). In addition, 26 drugs are targeting inputs identified by both algorithms, out of which the effect of nine has been studied for the treatment of breast cancer, and thirteen used in a clinical trial. In comparison, we found only three cancer-related existing drugs targeting the inputs only identified by the greedy algorithms, all of which are investigated in the treatment of, or under clinical investigation, for breast cancer.
The results look similar for the analyzed ovarian cancer networks. The genetic algorithm identified four specific top preferred inputs, out of which three are known to be of significance in ovarian cancer: DDR1122, SRC124, and ERBB2125. In contrast, only two were found by the greedy algorithms and not by the genetic algorithm, with one of significance in ovarian cancer: FGF1144. Both remaining inputs, one for each algorithm, are known to be important in other cancer types: PDPK1123 and HCK143. There are five additional drug-targets that have been identified by both algorithms, four of which of importance in ovarian cancer: PIM1153, SMO154, DDR2155, and CCL2157, and one in other types of cancer: PRKDC156. Of the related drug-targets, we found seventeen that are targeting the inputs identified only by the genetic algorithm, with seven under research for the treatment of ovarian cancer (afatinib126, dasatinib128, imatinib130, nintedanib134, pertuzumab136, ponatinib138, trastuzumab139), and seven part of an active or completed clinical trial (bosutinib127, dasatinib129, imatinib131, lapatinib132, nintedanib135, pertuzumab137, and trastuzumab emtansine140). Five more drugs are targeting inputs identified by both algorithms, with three of them part of a clinical trial. We found only four cancer-related drugs specific to the greedy algorithms, all of which are either researched, or under clinical investigation for ovarian cancer.
The results are consistently in favor of the genetic algorithm also in the case of the pancreatic cancer networks. There are three preferred inputs identified by both algorithms, two of which of importance in pancreatic cancer: CDK2184, and PIM1186, and one in other types of cancer: ABL1185. The genetic algorithm found six specific drug-targets, with five significant in pancreatic cancer: IGF1R164, SRC165, PDPK1166, AKT1167, and MTOR168, as opposed to only two for the greedy algorithms, both of significance in pancreatic cancer: GSK3B181, CDK4182. We found ten drugs specific to the genetic algorithm, out of which six investigated for the treatment of pancreatic cancer (arsenic trioxide169, cixutumumab171, everolimus172, genistein174, nintedanib175, and temsirolimus178), and four under clinical trials (arsenic trioxide170, everolimus173, nintedanib176, and temsirolimus179). In contrast, we found only one drug specific to the greedy algorithm. We found thirteen further drugs common to both algorithms, with two being researched, and four under clinical investigation for pancreatic cancer. The genetic algorithm uniquely identified ADCY1, currently not known to be targeted by any cancer-related drugs.
Furthermore, we found the drug fostamatinib, used for the treatment of rheumatoid arthritis and immune thrombocytopenic purpura199, which targets multiple inputs identified by the genetic algorithm in multiple runs for all studied cancer networks. Our algorithm thus suggests that the drug could potentially be used in cancer treatment. This idea is supported by several completed clinical trials for using fostamatinib in treating lymphoma200 and is investigated in an ongoing trial for ovarian cancer201.
Discussion
Applying network controllability for drug repurposing is not yet well-established. It is a very promising line of research that is currently hindered in part by the lack of powerful implementations of network controllability algorithms. This is where this paper and its algorithm contribute, making it possible to run detailed drug repurposing studies based on network controllability. We applied the algorithm to a few relatively small cancer examples, demonstrating its feasibility in the medical domain. Our demonstration was intended to show the potential of the network controllability approach to help in such studies. Our case studies suggest that this approach is promising in drug repurposing: we identified several approved drugs whose targets contribute to controlling the essential genes specific to other diseases than those the drugs were approved for. These results are to be considered as proof-of-concept, rather than fully fledged validated demonstrations of network control-based drug repurposing identification. Our search strategy was based on a genetic algorithm, where the population in each generation of the training of the algorithm is a set of valid solutions to the network controllability problem. The algorithm turned out to be scalable, with its performance staying strong even for large networks.
Our approach is to integrate the global interaction data into the directed networks and investigate a global optimization problem seeking to minimize the number of input nodes needed to control a target set. Genetic algorithms represent a known global optimization technique that permits for a global search of solutions throughout all parts of the network. They have been successfully used for solving combinatorial optimization problems, performing potentially better when compared to greedy algorithms23. Their use comes with limitations that we addressed in our implementation. To start with, evaluating the fitness function can generally be very computationally expensive. Within our approach, in order to calculate the fitness of a chromosome we first need to check its validity, which requires establishing if its corresponding Kalman matrix, whose size is dependent on the size of the target set, has a full rank. This operation can be computationally expensive for large matrices. We included in the “Supplementary Information” an overview of the function we used and its complexity. Another limitation refers to the genetic algorithms’ proneness to converging to a local optimum or arbitrary points, as opposed to the global optimum. To address this, we insert in each stage new random chromosomes (in addition to adding chromosomes obtained through crossover and mutation), to enrich the search space of the algorithm and escape the local optima. We also use elitism to ensure that each generation contains the distinct best solutions identified so far by the algorithm. Moreover, another limitation of the genetic algorithm is represented by the fact that the optimal result is not known and the quality of a solution is only comparable to the other solutions within a run. Thus, we alleviate the lack of a definite stopping criteria by running iteratively, each time until no new solutions have been identified within a predefined number of generations; by default, we set this to 100 generations.
The genetic algorithm comes by design with a set-limit on the maximum length of control paths from the input to the target nodes. We made this into a parameter whose value can be set by the user. Having this parameter is a feature of particularly important interest in applications in medicine, where the effects of a drug dissipate quickly over longer signaling paths. The focused search upstream of the target nodes led to the genetic algorithm drastically improving the percentage of FDA-approved drug targets selected in its solution, a clear step forward towards applications in combinatorial drug selection and drug repurposing. The drugs identified by our algorithm as potentially efficient for breast, ovarian, and pancreatic cancer correlate well with recent literature results, and some of our suggestions have already been subject to several clinical studies. This strengthens the potential of our approach for studies in synthetic lethality-driven drug repurposing.
There are several interesting questions around the applications of network science to drug repurposing, that deserve further investigations. On the experimental side, validating the predictions made by the network-based approaches would help drive this research line forward, and it would offer an insight into how to apply it to disease data. Some demonstrations already exist19, but more work is needed before the network analytics approach becomes a standard tool in this field. On the computational side, adding to the framework some quantitative aspects about the type and the weight of the interactions would help eliminate some of the false positive results. Also, adding non-linear interactions to the models would help extend the applicability of this method. A lot of work in this direction has already been done, e.g. on Boolean networks202,203,204, but the methods still suffer from scalability issues. Very large networks, with tens of thousands of interactions, are already practical based on linear network analyses, including the genetic algorithm proposed in this study.
Methods
We introduce briefly in the “Supplementary Information” the basic concepts of target structural network controllability and the Kalman matrix rank condition for the problem.
The algorithm takes as input a network given as a directed graph \(G=(V,E)\) and a list of target nodes \(T\subseteq V\), \(T=\{t_1,\ldots ,t_l\}\). We denote the graph’s adjacency matrix by \(A_G\). The algorithm gives as a result a set of input nodes \(I\subseteq V\) controlling the set T, with the objective being to minimize the size of I. The algorithm can also take as an additional, optional input a set \(P\subseteq V\) of so-called preferred nodes. In this case, the algorithm will aim for a double optimization objective: minimize the set I, while maximizing the number of elements from P included in I. Our typical application scenario is that of a network G consisting of directed protein-protein interactions specific to a disease mechanism of interest, with the set of targets T being a disease-specific set of essential genes, and the set of preferred nodes P a set of proteins targetable by available drugs or by specially designed compounds (e.g., inhibitors, small silencing molecules, etc.) The terminology we use to describe the algorithm, e.g., population/chromosome/crossover/mutation/fitness is standard in the genetic algorithm literature and refers to its conventions, rather than being suggestive of specifics in molecular biology.
Our algorithm starts by generating several solutions to the control problem, in the form of several “control sets” \(I_1, \ldots , I_m\); we discuss how this is achieved in the “Supplementary Information”. Each such solution is encoded as a “chromosome”, i.e., a vector of “genes” \([g_1,\ldots ,g_l]\), where for all \(1\le i\le l\), \(g_i\in V\) controls the target node \(t_i\in T\). In particular, \(g_i\) is an ancestor of \(t_i\) in graph G, for all \(1\le i\le l\). Note that a node can control simultaneously several other nodes in the network and so, the genes \(g_1,\ldots ,g_l\) of a chromosome are not necessarily distinct. In fact, the fewer the genes on a chromosome, the better its fitness will be, as we discuss in the “Supplementary Information”. The algorithm also implements maximizing the use of preferred nodes as genes on the chromosomes; the details are discussed in the “Supplementary Information”.
A set of chromosomes is called a population. Note that a chromosome will always encode a solution to our optimization problem, throughout the iterative run of the algorithm. Any population maintained by the algorithm consists of several such chromosomes, some better than others from the point of view of our optimization criteria, but all valid solutions to the target controllability problem to be solved.
The algorithm iteratively generates successive populations (sets of chromosomes) that get better at the optimization it aims to solve: the number of distinct genes on some chromosomes gets smaller and the proportion of preferred nodes among them gets higher. The algorithm stops after a number of iterations in which the quality of the solutions does not improve. To have a bounded running time even for large networks, we also added a stop condition after a maximum number of iterations; this was never reached during our tests. This pre-defined stop is necessary since the target structural controllability problem is known to be NP-hard and so, finding the optimal solution can require a prohibitively high number of steps, potentially exponential in the number of nodes in the network. The output consists of several solutions to the problem, represented by all the control sets in the final population obtained by the algorithm.
The initial population of solutions is randomly generated in such a way that each element selected for it is a solution to the target structural controllability problem \((A_G,I,T)\). To generate the next generation from the current one, we use three techniques:
-
Retain in the population the best solutions (from the point of view of the assessed optimization problem, as encoded in the fitness function). “Elitism” is used to conserve the best solutions (further discussed in the “Supplementary Information”).
-
Add random chromosomes (all being valid solutions to the optimization problem, albeit potentially of lower fitness score than some of the others in the population).
-
Generate new solutions/chromosomes resulting from combinations of those in the current population. A selection operator is used to choose the chromosomes which will produce offsprings for the following generation. New chromosomes are produced using crossover and mutation (discussed in detail in the “Supplementary Information”).
A list of all the parameters used by the genetic algorithm can be found in Table 3. The basic outline of the proposed genetic algorithm is described below. All operators are detailed in the “Supplementary Information”.
-
1.
Generate the initial population: we set \(t \leftarrow 0\) for the first generation. We initialize P(t) with a number of n randomly generated chromosomes.
-
2.
Preserve the fittest chromosomes: we evaluate the fitness of all chromosomes in P(t). We add to the next population \(P_{t+1}\) the \(p_e \cdot n\) chromosomes in the current generation with the highest fitness score, where \(0\le p_e<1\) is the ‘elitism’ parameter. If there are more chromosomes of equal fitness, the ones to be added are randomly chosen.
-
3.
Add random chromosomes: we add \(p_r \cdot n\) new randomly generated chromosomes to \(P(t + 1)\), where \(0\le p_r<1\) is the ‘randomness’ parameter.
-
4.
Add the offsprings of the current population: we apply two times the selection operator on P(t), obtaining two chromosomes of \(P_t\) selected randomly with a probability proportional to their fitness score. On the two selected chromosomes we apply the crossover operator, obtaining an offspring to be added to \(P(t + 1)\). The offspring is added in a mutated form with the mutation probability \(0\le p_m<1\). We continue applying this step until the number of chromosomes in \(P(t + 1)\) becomes n.
-
5.
Iterate: if the current index \(t<N\), the maximum number of generations, we set \(t \leftarrow t + 1\) and continue with Step 2.
-
6.
Output: we return the fittest chromosomes in the current generation as solutions to the problem and stop.
Data availability
All of the data and algorithm results are available in the application repository at42.
References
Kitano, H. Computational systems biology. Nature 420, 206–210. https://doi.org/10.1038/nature01254 (2002).
Tian, Q., Price, N. D. & Hood, L. Systems cancer medicine: Towards realization of predictive, preventive, personalized and participatory (p4) medicine. J. Internal Med. 271, 111–121. https://doi.org/10.1111/j.1365-2796.2011.02498.x (2012).
Barabási, A.-L., Gulbahce, N. & Loscalzo, J. Network medicine: A network-based approach to human disease. Nat. Rev. Genet. 12, 56–68. https://doi.org/10.1038/nrg2918 (2010).
Goh, K.-I. et al. The human disease network. Proc. Natl. Acad. Sci. 104, 8685–8690. https://doi.org/10.1073/pnas.0701361104 (2007).
Czeizler, E., Wu, K.-C., Gratie, C., Kanhaiya, K. & Petre, I. Structural target controllability of linear networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 15, 1217–1228. https://doi.org/10.1109/tcbb.2018.2797271 (2018).
Kanhaiya, K., Czeizler, E., Gratie, C. & Petre, I. Controlling directed protein interaction networks in cancer. Sci. Rep. https://doi.org/10.1038/s41598-017-10491-y (2017).
Ochsner, S. A. et al. The signaling pathways project, an integrated ‘omics knowledgebase for mammalian cellular signaling pathways. Sci. Data. https://doi.org/10.1038/s41597-019-0193-4 (2019).
Misselbeck, K. et al. A network-based approach to identify deregulated pathways and drug effects in metabolic syndrome. Nat. Commun. https://doi.org/10.1038/s41467-019-13208-z (2019).
Davis, M. M., Tato, C. M. & Furman, D. Systems immunology: Just getting started. Nat. Immunol. 18, 725–732. https://doi.org/10.1038/ni.3768 (2017).
Liu, X. et al. Computational methods for identifying the critical nodes in biological networks. Briefings Bioinform. 21, 486–497. https://doi.org/10.1093/bib/bbz011 (2019).
Cheng, F., Kovács, I. A. & Barabási, A.-L. Network-based prediction of drug combinations. Nat. Commun. https://doi.org/10.1038/s41467-019-09186-x (2019).
Kalman, R. E., Ho, Y. C. & Narendra, K. S. Controllability of linear dynamical systems. Contrib. Differ. Eqns. 1, 189–213 (1963).
Liu, Y.-Y., Slotine, J.-J. & Barabási, A.-L. Controllability of complex networks. Nature 473, 167–173. https://doi.org/10.1038/nature10011 (2011).
Gao, J., Liu, Y.-Y., D’Souza, R. M. & Barabási, A.-L. Target control of complex networks. Nat. Commun. https://doi.org/10.1038/ncomms6415 (2014).
Guo, W.-F. et al. Constrained target controllability of complex networks. J. Stat. Mech. Theory Exp. 2017, 063402. https://doi.org/10.1088/1742-5468/aa6de6 (2017).
Ebrahimi, A., Nowzari-Dalini, A., Jalili, M. & Masoudi-Nejad, A. Target controllability with minimal mediators in complex biological networks. Genomics 112, 4938–4944. https://doi.org/10.1016/j.ygeno.2020.09.003 (2020).
Molnár, F., Sreenivasan, S., Szymanski, B. K. & Korniss, G. Minimum dominating sets in scale-free network ensembles. Sci. Rep. https://doi.org/10.1038/srep01736 (2013).
Yan, G. et al. Network control principles predict neuron function in the Caenorhabditis elegans connectome. Nature 550, 519–523. https://doi.org/10.1038/nature24056 (2017).
Ding, Y.-Y. et al. Network analysis reveals synergistic genetic dependencies for rational combination therapy in Philadelphia chromosome-like acute lymphoblastic leukemia. Clin. Cancer Res. 27, 5109–5122. https://doi.org/10.1158/1078-0432.ccr-21-0553 (2021).
Guo, W.-F. et al. Network controllability-based algorithm to target personalized driver genes for discovering combinatorial drugs of individual patients. Nucleic Acids Res. 49, e37. https://doi.org/10.1093/nar/gkaa1272 (2021).
Rancati, G., Moffat, J., Typas, A. & Pavelka, N. Emerging and evolving concepts in gene essentiality. Nat. Rev. Genet. 19, 34–49. https://doi.org/10.1038/nrg.2017.74 (2017).
Siminea, N. et al. Network analytics for drug repurposing in COVID-19. Brief. Bioinform. https://doi.org/10.1093/bib/bbab490 (2021).
Whitley, D. & Sutton, A. M. Genetic algorithms—A survey of models and methods. In Handbook of Natural Computing, 637–671 (Springer Berlin Heidelberg, 2012). https://doi.org/10.1007/978-3-540-92910-9_21.
Park, K. A review of computational drug repurposing. Transl. Clin. Pharmacol. 27, 59. https://doi.org/10.12793/tcp.2019.27.2.59 (2019).
Habibi, M., Taheri, G. & Aghdam, R. A SARS-CoV-2 (COVID-19) biological network to find targets for drug repurposing. Sci. Rep. https://doi.org/10.1038/s41598-021-88427-w (2021).
Ackerman, E. & Shoemaker, J. Network controllability-based prioritization of candidates for SARS-CoV-2 drug repositioning. Viruses 12, 1087. https://doi.org/10.3390/v12101087 (2020).
Menden, M. P. et al. Machine learning prediction of cancer cell sensitivity to drugs based on genomic and chemical properties. PLoS ONE 8, e61318. https://doi.org/10.1371/journal.pone.0061318 (2013).
Chen, H., Engkvist, O., Wang, Y., Olivecrona, M. & Blaschke, T. The rise of deep learning in drug discovery. Drug Discov. Today 23, 1241–1250. https://doi.org/10.1016/j.drudis.2018.01.039 (2018).
Cabrera-Andrade, A. et al. A multi-objective approach for anti-osteosarcoma cancer agents discovery through drug repurposing. Pharmaceuticals 13, 409. https://doi.org/10.3390/ph13110409 (2020).
Cheng, D. et al. PolySearch: A web-based text mining system for extracting relationships between human diseases, genes, mutations, drugs and metabolites. Nucleic Acids Res. 36, W399–W405. https://doi.org/10.1093/nar/gkn296 (2008).
Chen, B., Ding, Y. & Wild, D. J. Assessing drug target association using semantic linked data. PLoS Comput. Biol. 8, e1002574. https://doi.org/10.1371/journal.pcbi.1002574 (2012).
Huang, Q., Wu, L.-Y. & Zhang, X.-S. Corbi: A new r package for biological network alignment and querying. BMC Syst. Biol. https://doi.org/10.1186/1752-0509-7-s2-s6 (2013).
Rakshit, H., Chatterjee, P. & Roy, D. A bidirectional drug repositioning approach for Parkinson’s disease through network-based inference. Biochem. Biophys. Res. Commun. 457, 280–287. https://doi.org/10.1016/j.bbrc.2014.12.101 (2015).
Hagberg, A. A., Schult, D. A. & Swart, P. J. Exploring network structure, dynamics, and function using networkx. in Proceedings of the 7th Python in Science Conference, 11–15 (2008).
Koh, J. L. Y. et al. COLT-cancer: Functional genetic screening resource for essential genes in human cancer cell lines. Nucleic Acids Res. 40, D957–D963. https://doi.org/10.1093/nar/gkr959 (2011).
The UniProt Consortium. et al. UniProt: The universal protein knowledgebase in 2021. Nucleic Acids Res. 49, 480–489. https://doi.org/10.1093/nar/gkaa1100 (2020).
Perfetto, L. et al. SIGNOR: A database of causal relationships between biological entities. Nucleic Acids Res. 44, D548–D554. https://doi.org/10.1093/nar/gkv1048 (2015).
Wishart, D. S. et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 46, D1074–D1082. https://doi.org/10.1093/nar/gkx1037 (2017).
Moradi, M., Goliaei, S. & Foroughmand-Araabi, M.-H. A Boolean network control algorithm guided by forward dynamic programming. PLOS ONE 14, e0215449. https://doi.org/10.1371/journal.pone.0215449 (2019).
Baudin, A., Paul, S., Su, C. & Pang, J. Controlling large Boolean networks with single-step perturbations. Bioinformatics 35, i558–i567. https://doi.org/10.1093/bioinformatics/btz371 (2019).
Murota, K. & Poljak, S. Note on a graph-theoretic criterion for structural output controllability. IEEE Trans. Autom. Control 35, 939–942. https://doi.org/10.1109/9.58507 (1990).
Popescu, V. GeneticAlgNetControl (2021). https://github.com/Vilksar/GeneticAlgNetControl. Version 1.0 (Accessed October 26, 2021).
Chen, F. et al. VDAC1 conversely correlates with CYTC expression and predicts poor prognosis in human breast cancer patients. Oxidative Med. Cell. Longevity 2021, 1–13. https://doi.org/10.1155/2021/7647139 (2021).
Jing, H., Song, J. & Zheng, J. Discoidin domain receptor 1: New star in cancer-targeted therapy and its complex role in breast carcinoma (review). Oncol. Lett. https://doi.org/10.3892/ol.2018.7795 (2018).
Holla, V. R. et al. ALK: A tyrosine kinase target for cancer therapy. Mol. Case Studies 3, a001115. https://doi.org/10.1101/mcs.a001115 (2017).
Finn, R. Targeting SRC in breast cancer. Ann. Oncol. 19, 1379–1386. https://doi.org/10.1093/annonc/mdn291 (2008).
Stanek, L., Tesarova, P., Vocka, M. & Petruzelka, L. Analysis of the JAK2 gene in triple-negative breast cancer (TNBC). Ann. Oncol. 29, viii95. https://doi.org/10.1093/annonc/mdy272.291 (2018).
Levine, K. M., Ding, K., Chen, L. & Oesterreich, S. FGFR4: A promising therapeutic target for breast cancer and other solid tumors. Pharmacol. Therap. 214, 107590. https://doi.org/10.1016/j.pharmthera.2020.107590 (2020).
Kirchhoff, D. et al. IL3ra-targeting antibody–drug conjugate BAY-943 with a kinesin spindle protein inhibitor payload shows efficacy in preclinical models of hematologic malignancies. Cancers 12, 3464. https://doi.org/10.3390/cancers12113464 (2020).
Elsberger, B. et al. Breast cancer patients’ clinical outcome measures are associated with SRC kinase family member expression. Br. J. Cancer 103, 899–909. https://doi.org/10.1038/sj.bjc.6605829 (2010).
Brady, N. J., Chuntova, P., Bade, L. K. & Schwertfeger, K. L. The FGF/FGF receptor axis as a therapeutic target in breast cancer. Expert Rev. Endocrinol. Metab. 8, 391–402. https://doi.org/10.1586/17446651.2013.811910 (2013).
Fondazione per la Medicina Personalizzata. The Rome trial from histology to target: The road to personalize target therapy and immunotherapy (ROME) (2021). https://clinicaltrials.gov/ct2/show/NCT04591431 (Accessed October 14, 2021).
McKeage, K. Alectinib: A review of its use in advanced ALK-rearranged non-small cell lung cancer. Drugs 75, 75–82. https://doi.org/10.1007/s40265-014-0329-y (2014).
Georgetown University. Wi231696: Bosutinib, palbocicilib and fulvestrant for hr+her2- advanced breast cancer refractory to a cdk4/6 inhibitor (2019). https://clinicaltrials.gov/ct2/show/NCT03854903 (Accessed October 14, 2021).
von Amsberg, G. K. & Schafhausen, P. Bosutinib in the management of chronic myelogenous leukemia. Biol. Targets Ther. https://doi.org/10.2147/btt.s30182 (2013).
Shaw, A. T. et al. Ceritinib inALK-rearranged non-small-cell lung cancer. N. Engl. J. Med. 370, 1189–1197. https://doi.org/10.1056/nejmoa1311107 (2014).
Ayoub, N., Al-Shami, K., Alqudah, M. A. Y. & Mhaidat, N. Crizotinib, a MET inhibitor, inhibits growth, migration, and invasion of breast cancer cells in vitro and synergizes with chemotherapeutic agents. Oncol. Targets Therap. 10, 4869–4883. https://doi.org/10.2147/ott.s148604 (2017).
Royal Marsden NHS Foundation Trust. Crizotinib in Lobular Breast, Diffuse Gastric and Triple Negative Lobular Breast Cancer or CDH1-mutated Solid Tumours (ROLo) (2018). https://clinicaltrials.gov/ct2/show/NCT03620643 (Accessed October 14, 2021).
Tian, J. et al. Dasatinib sensitises triple negative breast cancer cells to chemotherapy by targeting breast cancer stem cells. Br. J. Cancer 119, 1495–1507. https://doi.org/10.1038/s41416-018-0287-3 (2018).
University of Wisconsin, Madison. Window of Opportunity Trial of Dasatinib in Operable Triple Negative Breast Cancers With nEGFR (2016). https://clinicaltrials.gov/ct2/show/NCT02720185 (Accessed October 14, 2021).
Al-Salama, Z. T. & Keam, S. J. Entrectinib: First global approval. Drugs 79, 1477–1483. https://doi.org/10.1007/s40265-019-01177-y (2019).
Fathi, A. T. & Chen, Y.-B. The role of FLT3 inhibitors in the treatment of FLT3-mutated acute myeloid leukemia. Eur. J. Haematol. 98, 330–336. https://doi.org/10.1111/ejh.12841 (2017).
Stanford University. Study of Infigratinib in Combination with Tamoxifen or with Fulvestrant and Palbociclib in Hormone Receptor Positive, HER2 Negative, FGFR Altered Advanced Breast Cancer (2020). https://clinicaltrials.gov/ct2/show/NCT04504331 (Accessed October 14, 2021).
Botrus, G., Raman, P., Oliver, T. & Bekaii-Saab, T. Infigratinib (BGJ398): An investigational agent for the treatment of FGFR-altered intrahepatic cholangiocarcinoma. Expert Opin. Investig. Drugs 30, 309–316. https://doi.org/10.1080/13543784.2021.1864320 (2021).
Lim, J. S. J. et al. Clinical efficacy and molecular effects of lenvatinib (len) and letrozole (let) in hormone receptor-positive (HR+) metastatic breast cancer (MBC). J. Clin. Oncol. 38, 1019. https://doi.org/10.1200/jco.2020.38.15_suppl.1019 (2020).
University of Illinois at Chicago. Preoperative Lenvatinib Plus Pembrolizumab in Early-Stage Triple-Negative Breast Cancer (TNBC) (2020). https://clinicaltrials.gov/ct2/show/NCT04427293 (Accessed October 14, 2021).
Shaw, A. T. et al. Lorlatinib in non-small-cell lung cancer with ALK or ROS1 rearrangement: An international, multicentre, open-label, single-arm first-in-man phase 1 trial. Lancet. Oncol. 18, 1590–1599. https://doi.org/10.1016/s1470-2045(17)30680-0 (2017).
Quintela-Fandino, M. et al. Nintedanib plus letrozole in early breast cancer: A phase 0/i pharmacodynamic, pharmacokinetic, and safety clinical trial of combined FGFR1 and aromatase inhibition. Breast Cancer Res. https://doi.org/10.1186/s13058-019-1152-x (2019).
Centro Nacional de Investigaciones Oncologicas CARLOS III. Nintedanib+Letrozole in Postmenopausal Women With Breast Cancer: Clinical Trial Safety and Pharmacodynamics (2015). https://clinicaltrials.gov/ct2/show/NCT02619162 (Accessed October 14, 2021).
Rizzo, A., Ricci, A. D. & Brandi, G. Pemigatinib: Hot topics behind the first approval of a targeted therapy in cholangiocarcinoma. Cancer Treatment Res. Commun. 27, 100337. https://doi.org/10.1016/j.ctarc.2021.100337 (2021).
Musumeci, F., Greco, C., Grossi, G., Molinari, A. & Schenone, S. Recent studies on ponatinib in cancers other than chronic myeloid leukemia. Cancers 10, 430. https://doi.org/10.3390/cancers10110430 (2018).
Russo, A. et al. New targets in lung cancer (excluding EGFR, ALK, ROS1). Curr. Oncol. Rep. https://doi.org/10.1007/s11912-020-00909-8 (2020).
Ekyalongo, R. C. & Yee, D. Revisiting the IGF-1r as a breast cancer target. NPJ Precis. Oncol. https://doi.org/10.1038/s41698-017-0017-y (2017).
Martorana, F. et al. AKT inhibitors: New weapons in the fight against breast cancer? Front. Pharmacol. https://doi.org/10.3389/fphar.2021.662232 (2021).
Rowinsky, E. K. et al. IMC-a12, a human IgG1 monoclonal antibody to the insulin-like growth factor i receptor: Fig. 1. Clin. Cancer Res. 13, 5549s–5555s. https://doi.org/10.1158/1078-0432.ccr-07-1109 (2007).
Eli Lilly and Company. A Study for Safety and Effectiveness of IMC-A12 by Itself or Combined with Antiestrogens to Treat Breast Cancer (2008). https://clinicaltrials.gov/ct2/show/NCT00728949 (Accessed October 14, 2021).
Fan, P. et al. Genistein decreases the breast cancer stem-like cell population through hedgehog pathway. Stem Cell Res. Therapy 4, 146. https://doi.org/10.1186/scrt357 (2013).
Barbara Ann Karmanos Cancer Institute. Gemcitabine Hydrochloride and Genistein in Treating Women with Stage IV Breast Cancer (2008). https://clinicaltrials.gov/ct2/show/NCT00244933 (Accessed October 14, 2021).
Wang, Y. et al. Arsenic trioxide induces the apoptosis of human breast cancer MCF-7 cells through activation of caspase-3 and inhibition of HERG channels. Exp. Therap. Med. 2, 481–486. https://doi.org/10.3892/etm.2011.224 (2011).
Almeida, M., Soares, M., Ramalhinho, A. C., Moutinho, J. F. & Breitenfeld, L. Prognosis of hormone-dependent breast cancer seems to be influenced by KEAP1, NRF2 and GSTM1 genetic polymorphisms. Mol. Biol. Rep. 46, 3213–3224. https://doi.org/10.1007/s11033-019-04778-8 (2019).
Brasó-Maristany, F. et al. PIM1 kinase regulates cell death, tumor growth and chemotherapy response in triple-negative breast cancer. Nat. Med. 22, 1303–1313. https://doi.org/10.1038/nm.4198 (2016).
Dentelli, P., Rosso, A., Olgasi, C., Camussi, G. & Brizzi, M. F. IL-3 is a novel target to interfere with tumor vasculature. Oncogene 30, 4930–4940. https://doi.org/10.1038/onc.2011.204 (2011).
Gonzalez, M. E. et al. Mesenchymal stem cell-induced DDR2 mediates stromal-breast cancer interactions and metastasis growth. Cell Rep. 18, 1215–1228. https://doi.org/10.1016/j.celrep.2016.12.079 (2017).
Nigro, C. L., Rusmini, M. & Ceccherini, I. RET in breast cancer: Pathogenic implications and mechanisms of drug resistance. Cancer Drug Resistance. https://doi.org/10.20517/cdr.2019.66 (2019).
Masuda, H. et al. Role of epidermal growth factor receptor in breast cancer. Breast Cancer Res. Treatment 136, 331–345. https://doi.org/10.1007/s10549-012-2289-9 (2012).
Hurvitz, S. A., Shatsky, R. & Harbeck, N. Afatinib in the treatment of breast cancer. Expert Opin. Investig. Drugs 23, 1039–1047. https://doi.org/10.1517/13543784.2014.924505 (2014).
He, X. A Study of HER2+ Breast Cancer Patients wth Active Brain Metastases Treated with Afatinib & T-DM1 vs. T-DM1 Alone (HER2BAT) (2019). https://clinicaltrials.gov/ct2/show/NCT04158947 (Accessed October 14, 2021).
Wu, K. et al. Flavopiridol and trastuzumab synergistically inhibit proliferation of breast cancer cells: Association with selective cooperative inhibition of cyclin d1-dependent kinase and akt signaling pathways 1 this work was supported in part by nih grants ro1ca708. Mol. Cancer Therap. 1, 695–706 (2002).
Mayo Clinic. Flavopiridol Plus Cisplatin or Carboplatin in Treating Patients with Advanced Solid Tumors (2003). https://clinicaltrials.gov/ct2/show/NCT00003690 (Accessed October 14, 2021).
Neijssen, J. et al. Discovery of amivantamab (JNJ-61186372), a bispecific antibody targeting EGFR and MET. J. Biol. Chem. 296, 100641. https://doi.org/10.1016/j.jbc.2021.100641 (2021).
Suzuki, T. et al. Pharmacological characterization of MP-412 (AV-412), a dual epidermal growth factor receptor and ErbB2 tyrosine kinase inhibitor. Cancer Sci. 98, 1977–1984. https://doi.org/10.1111/j.1349-7006.2007.00613.x (2007).
Rashda, S. & Gerber, D. E. A crowded, but still varied, space: Brigatinib in anaplastic lymphoma kinase-rearranged non-small cell lung cancer. Transl. Cancer Res. 6, S78–S82. https://doi.org/10.21037/tcr.2017.02.12 (2017).
Gurdal, H., Tuglu, M., Bostanabad, S. & Dalkili, B. Partial agonistic effect of cetuximab on epidermal growth factor receptor and src kinase activation in triple-negative breast cancer cell lines. Int. J. Oncol. https://doi.org/10.3892/ijo.2019.4697 (2019).
Merck KGaA, Darmstadt, Germany. Cetuximab and Cisplatin in the Treatment of “Triple Negative” (Estrogen Receptor [ER] Negative, Progesterone Receptor [PgR] Negative, and Human Epidermal Growth Factor Receptor 2 [HER2] Negative) Metastatic Breast Cancer (BALI-1) (2007). https://clinicaltrials.gov/ct2/show/NCT00463788 (Accessed October 14, 2021).
Kalous, O. et al. Dacomitinib (PF-00299804), an irreversible pan-HER inhibitor, inhibits proliferation of HER2-amplified breast cancer cell lines resistant to trastuzumab and lapatinib. Mol. Cancer Therap. 11, 1978–1987. https://doi.org/10.1158/1535-7163.mct-11-0730 (2012).
Nishina, T. et al. Safety, pharmacokinetic, and pharmacodynamics of erdafitinib, a pan-fibroblast growth factor receptor (FGFR) tyrosine kinase inhibitor, in patients with advanced or refractory solid tumors. Investig. New Drugs 36, 424–434. https://doi.org/10.1007/s10637-017-0514-4 (2017).
Vanderbilt-Ingram Cancer Center. Fulvestrant, Palbociclib and Erdafitinib in ER+/HER2-/FGFR-amplified Metastatic Breast Cancer (2017). https://clinicaltrials.gov/ct2/show/NCT03238196 (Accessed October 14, 2021).
Bao, B. et al. Treating triple negative breast cancer cells with erlotinib plus a select antioxidant overcomes drug resistance by targeting cancer cell heterogeneity. Sci. Rep. https://doi.org/10.1038/srep44125 (2017).
Green, M. et al. Gefitinib treatment in hormone-resistant and hormone receptor-negative advanced breast cancer. Ann. Oncol. 20, 1813–1817. https://doi.org/10.1093/annonc/mdp202 (2009).
AstraZeneca. IRESSA (Gefitinib) in Breast Cancer Patients (2008). https://clinicaltrials.gov/ct2/show/NCT00632723 (Accessed October 14, 2021).
Tan, F. et al. Icotinib, a selective EGF receptor tyrosine kinase inhibitor, for the treatment of non-small-cell lung cancer. Future Oncol. 11, 385–397. https://doi.org/10.2217/fon.14.249 (2015).
Mundhenke, C. et al. Effects of imatinib on breast cancer cell biology in vitro. J. Clin. Oncol. 23, 3210. https://doi.org/10.1200/jco.2005.23.16_suppl.3210 (2005).
Novartis Pharmaceuticals. Efficacy and Safety of Imatinib and Vinorelbine in Patients with Advanced Breast Cancer (INV181) (2006). https://clinicaltrials.gov/ct2/show/NCT00372476 (Accessed October 14, 2021).
Burris, H. A. Dual kinase inhibition in the treatment of breast cancer: Initial experience with the EGFR/ErbB-2 inhibitor lapatinib. Oncologist 9, 10–15. https://doi.org/10.1634/theoncologist.9-suppl_3-10 (2004).
Socinski, M. A. Antibodies to the epidermal growth factor receptor in non–small cell lung cancer: Current status of matuzumab and panitumumab. Clin. Cancer Res. 13, 4597s–4601s. https://doi.org/10.1158/1078-0432.ccr-07-0335 (2007).
Gonzalvez, F. et al. Mobocertinib (TAK-788): A targeted inhibitor of EGFR exon 20 insertion mutants in non-small cell lung cancer. Cancer Discov. 11, 1672–1687. https://doi.org/10.1158/2159-8290.cd-20-1683 (2021).
Garnock-Jones, K. P. Necitumumab: First global approval. Drugs 76, 283–289. https://doi.org/10.1007/s40265-015-0537-0 (2016).
Chan, A. et al. Final efficacy results of neratinib in HER2-positive hormone receptor-positive early-stage breast cancer from the phase III ExteNET trial. Clin. Breast Cancer 21, 80–91.e7. https://doi.org/10.1016/j.clbc.2020.09.014 (2021).
Puma Biotechnology, Inc. Study Evaluating The Effects of Neratinib After Adjuvant Trastuzumab in Women with Early Stage Breast Cancer (ExteNET) (2009). https://clinicaltrials.gov/ct2/show/NCT00878709 (Accessed October 14, 2021).
Liao, B.-C., Lin, C.-C., Lee, J.-H. & Yang, J.C.-H. Update on recent preclinical and clinical studies of t790m mutant-specific irreversible epidermal growth factor receptor tyrosine kinase inhibitors. J. Biomed. Sci. https://doi.org/10.1186/s12929-016-0305-9 (2016).
Shea, M., Costa, D. B. & Rangachari, D. Management of advanced non-small cell lung cancers with known mutations or rearrangements: Latest evidence and treatment approaches. Therap. Adv. Respir. Disease 10, 113–129. https://doi.org/10.1177/1753465815617871 (2015).
Keating, G. M. Panitumumab. Drugs 70, 1059–1078. https://doi.org/10.2165/11205090-000000000-00000 (2010).
M.D. Anderson Cancer Center. Carboplatin and Paclitaxel With or Without Panitumumab in Treating Patients with Invasive Triple Negative Breast Cancer (2016). https://clinicaltrials.gov/ct2/show/NCT02876107 (Accessed October 14, 2021).
Yoshimura, N. et al. EKB-569, a new irreversible epidermal growth factor receptor tyrosine kinase inhibitor, with clinical activity in patients with non-small cell lung cancer with acquired resistance to gefitinib. Lung Cancer 51, 363–368. https://doi.org/10.1016/j.lungcan.2005.10.006 (2006).
Mehta, M. et al. Regorafenib sensitizes human breast cancer cells to radiation by inhibiting multiple kinases and inducing DNA damage. Int. J. Radiat. Biol. 97, 1109–1120. https://doi.org/10.1080/09553002.2020.1730012 (2020).
Luca, A. D. et al. Vandetanib as a potential treatment for breast cancer. Expert Opin. Investig. Drugs 23, 1295–1303. https://doi.org/10.1517/13543784.2014.942034 (2014).
Genzyme, a Sanofi Company. This Study is to Assess the Efficacy and Safety of ZD6474 in Subjects with Metastatic Breast Cancer (2002). https://clinicaltrials.gov/ct2/show/NCT00034918 (Accessed October 14, 2021).
Liu, C.-Y. et al. Varlitinib downregulates HER/ERK signaling and induces apoptosis in triple negative breast cancer cells. Cancers 11, 105. https://doi.org/10.3390/cancers11010105 (2019).
Aslan Pharmaceuticals. Study of ASLAN001 in Combination with Capecitabine in MBC that has Failed on Prior Trastuzumab (2015). https://clinicaltrials.gov/ct2/show/NCT02338245 (Accessed October 14, 2021).
King, E. R. & Wong, K.-K. Insulin-like growth factor: Current concepts and new developments in cancer therapy. Recent Patents Anti-cancer Drug Discov. 7, 14–30. https://doi.org/10.2174/157489212798357930 (2012).
Zou, Y.-X. et al. The impacts of zanubrutinib on immune cells in patients with chronic lymphocytic leukemia/small lymphocytic lymphoma. Hematol. Oncol. 37, 392–400. https://doi.org/10.1002/hon.2667 (2019).
Quan, J., Yahata, T., Adachi, S., Yoshihara, K. & Tanaka, K. Identification of receptor tyrosine kinase, discoidin domain receptor 1 (DDR1), as a potential biomarker for serous ovarian cancer. Int. J. Mol. Sci. 12, 971–982. https://doi.org/10.3390/ijms12020971 (2011).
Domrachev, B., Singh, S., Li, D. & Rudloff, U. Mini-review: PDPK1 (3-phosphoinositide dependent protein kinase-1), an emerging cancer stem cell target. J. Cancer Treatment Diagnosis 5, 30–35. https://doi.org/10.29245/2578-2967/2021/1.1194 (2021).
Simpkins, F. et al. Dual SRC and MEK inhibition decreases ovarian cancer growth and targets tumor initiating stem-like cells. Clin. Cancer Res. 24, 4874–4886. https://doi.org/10.1158/1078-0432.ccr-17-3697 (2018).
Luo, H., Xu, X., Ye, M., Sheng, B. & Zhu, X. The prognostic value of HER2 in ovarian cancer: A meta-analysis of observational studies. PLOS ONE 13, e0191972. https://doi.org/10.1371/journal.pone.0191972 (2018).
Shepherd-Littlejohn, A. L., Hanft, W. J., Kennedy, V. A. & Alvarez, E. A. Afatinib use in recurrent epithelial ovarian carcinoma. Gynecol. Oncol. Rep. 29, 70–72. https://doi.org/10.1016/j.gore.2019.07.001 (2019).
Abdel Karim, N. Bosutinib in Combination with Pemetrexed in Patients with Selected Metastatic Solid Tumors (2017). https://clinicaltrials.gov/ct2/show/NCT03023319 (Accessed October 14, 2021).
Xiao, J. et al. Dasatinib enhances antitumor activity of paclitaxel in ovarian cancer through src signaling. Mol. Med. Rep. 12, 3249–3256. https://doi.org/10.3892/mmr.2015.3784 (2015).
National Cancer Institute (NCI). Dasatinib in Treating Patients with Recurrent or Persistent Ovarian, Fallopian Tube, Endometrial or Peritoneal Cancer (2014). https://clinicaltrials.gov/ct2/show/NCT02059265 (Accessed October 14, 2021).
Matei, D., Chang, D. D. & Jeng, M.-H. Imatinib mesylate (gleevec) inhibits ovarian cancer cell growth through a mechanism dependent on platelet-derived growth factor receptor alpha and akt inactivation. Clin. Cancer Res. 10, 681–690. https://doi.org/10.1158/1078-0432.ccr-0754-03 (2004).
Henry M. Jackson Foundation for the Advancement of Military Medicine. Gleevec and Gemzar in Patients With Epithelial Ovarian Cancer (2009). https://clinicaltrials.gov/ct2/show/NCT00928642 (Accessed October 14, 2021).
Frederick R., & Ueland, M. D. Dose Escalation of Lapatinib with Paclitaxel in Ovarian Cancer (2020). https://clinicaltrials.gov/ct2/show/NCT04608409 (Accessed October 14, 2021).
Bang, Y. et al. First-in-human phase 1 study of margetuximab (MGAH22), an fc-modified chimeric monoclonal antibody, in patients with HER2-positive advanced solid tumors. Ann. Oncol. 28, 855–861. https://doi.org/10.1093/annonc/mdx002 (2017).
Barra, F., Laganà, A. S., Ghezzi, F., Casarin, J. & Ferrero, S. Nintedanib for advanced epithelial ovarian cancer: A change of perspective? Summary of evidence from a systematic review. Gynecol. Obstetr. Investig. 84, 107–117. https://doi.org/10.1159/000493361 (2018).
Ingelheim, B. LUME-Ovar 1: Nintedanib (BIBF 1120) or Placebo in Combination with Paclitaxel and Carboplatin in First Line Treatment of Ovarian Cancer (2009). https://clinicaltrials.gov/ct2/show/NCT01015118 (Accessed October 14, 2021).
Langdon, S. P., Faratian, D., Nagumo, Y., Mullen, P. & Harrison, D. J. Pertuzumab for the treatment of ovarian cancer. Expert Opin. Biol. Therapy 10, 1113–1120. https://doi.org/10.1517/14712598.2010.487062 (2010).
Roche, H. Pertuzumab in Platinum-Resistant Low Human Epidermal Growth Factor Receptor 3 (HER3) Messenger Ribonucleic Acid (mRNA) Epithelial Ovarian Cancer (PENELOPE) (2012). https://clinicaltrials.gov/ct2/show/NCT01684878 (Accessed October 14, 2021).
Lang, J. D. et al. Ponatinib shows potent antitumor activity in small cell carcinoma of the ovary hypercalcemic type (SCCOHT) through multikinase inhibition. Clin. Cancer Res. 24, 1932–1943. https://doi.org/10.1158/1078-0432.ccr-17-1928 (2018).
Wilken, J. A., Webster, K. T. & Maihle, N. J. Trastuzumab sensitizes ovarian cancer cells to EGFR-targeted therapeutics. J. Ovarian Res. https://doi.org/10.1186/1757-2215-3-7 (2010).
Roche, H. A Study Evaluating the Efficacy and Safety of Biomarker-Driven Therapies in Patients with Persistent or Recurrent Rare Epithelial Ovarian Tumors (2021). https://clinicaltrials.gov/ct2/show/NCT04931342 (Accessed October 14, 2021).
Phillips, G. D. L. et al. Targeting HER2-positive breast cancer with trastuzumab-DM1, an antibody–cytotoxic drug conjugate. Cancer Res. 68, 9280–9290. https://doi.org/10.1158/0008-5472.can-08-1776 (2008).
Kulukian, A. et al. Preclinical activity of HER2-selective tyrosine kinase inhibitor tucatinib as a single agent or in combination with trastuzumab or docetaxel in solid tumor models. Mol. Cancer Therap. 19, 976–987. https://doi.org/10.1158/1535-7163.mct-19-0873 (2020).
Poh, A. R., O’Donoghue, R. J. & Ernst, M. Hematopoietic cell kinase (HCK) as a therapeutic target in immune and cancer cells. Oncotarget 6, 15752–15771. https://doi.org/10.18632/oncotarget.4199 (2015).
Manousakidi, S. et al. FGF1 induces resistance to chemotherapy in ovarian granulosa tumor cells through regulation of p53 mitochondrial localization. Oncogenesis. https://doi.org/10.1038/s41389-018-0033-y (2018).
Zhang, Q.-F. et al. CDK4/6 inhibition promotes immune infiltration in ovarian cancer and synergizes with PD-1 blockade in a b cell-dependent manner. Theranostics 10, 10619–10633. https://doi.org/10.7150/thno.44871 (2020).
Jonsson Comprehensive Cancer Center. Abemaciclib for the Treatment of Recurrent Ovarian or Endometrial Cancer (2020). https://clinicaltrials.gov/ct2/show/NCT04469764 (Accessed October 14, 2021).
Raju, U., Nakata, E., Mason, K. A., Ang, K. K. & Milas, L. Flavopiridol, a cyclin-dependent kinase inhibitor, enhances radiosensitivity of ovarian carcinoma cells. Cancer Res. 63, 3263–3267 (2003).
National Cancer Institute (NCI). Cisplatin and Flavopiridol in Treating Patients with Advanced Ovarian Epithelial Cancer or Primary Peritoneal Cancer (2004). https://clinicaltrials.gov/ct2/show/NCT00083122 (Accessed October 14, 2021).
Lee, D. W. & Ho, G. F. Palbociclib in the treatment of recurrent ovarian cancer. Gyncol. Oncol. Rep. 34, 100626. https://doi.org/10.1016/j.gore.2020.100626 (2020).
Latin American Cooperative Oncology Group. Palbociclib Plus Letrozole Treatment After Progression to Second Line Chemotherapy for Women with ER/PR-positive Ovarian Cancer. (LACOG1018) (2019). https://clinicaltrials.gov/ct2/show/NCT03936270 (Accessed October 14, 2021).
Im, S.-A. et al. Overall survival with ribociclib plus endocrine therapy in breast cancer. N. Engl. J. Med. 381, 307–316. https://doi.org/10.1056/nejmoa1903765 (2019).
Buckanovich, R. Ribociclib (Ribociclib (LEE-011)) with Platinum-based Chemotherapy in Recurrent Platinum Sensitive Ovarian Cancer (2017). https://clinicaltrials.gov/ct2/show/NCT03056833 (Accessed October 14, 2021).
Wu, Y. et al. Pim1 promotes cell proliferation and regulates glycolysis via interaction with MYC in ovarian cancer. OncoTargets Ther. 11, 6647–6656. https://doi.org/10.2147/ott.s180520 (2018).
Szkandera, J., Kiesslich, T., Haybaeck, J., Gerger, A. & Pichler, M. Hedgehog signaling pathway in ovarian cancer. Int. J. Mol. Sci. 14, 1179–1196. https://doi.org/10.3390/ijms14011179 (2013).
Grither, W. R. et al. TWIST1 induces expression of discoidin domain receptor 2 to promote ovarian cancer metastasis. Oncogene 37, 1714–1729. https://doi.org/10.1038/s41388-017-0043-9 (2018).
Sun, G. et al. PRKDC regulates chemosensitivity and is a potential prognostic and predictive marker of response to adjuvant chemotherapy in breast cancer patients. Oncol. Rep. 37, 3536–3542. https://doi.org/10.3892/or.2017.5634 (2017).
Fader, A. N. et al. Ccl2 expression in primary ovarian carcinoma is correlated with chemotherapy response and survival outcomes. Anticancer Res. 30, 4791–4798 (2010).
Xie, H., Paradise, B. D., Ma, W. W. & Fernandez-Zapico, M. E. Recent advances in the clinical targeting of hedgehog/GLI signaling in cancer. Cells 8, 394. https://doi.org/10.3390/cells8050394 (2019).
Grothey, A., Blay, J.-Y., Pavlakis, N., Yoshino, T. & Bruix, J. Evolving role of regorafenib for the treatment of advanced cancers. Cancer Treatment Rev. 86, 101993. https://doi.org/10.1016/j.ctrv.2020.101993 (2020).
National Cancer Centre, Singapore. Use of Regorafenib in Recurrent Epithelial Ovarian Cancer (2016). https://clinicaltrials.gov/ct2/show/NCT02736305 (Accessed October 14, 2021).
Mahadevan, D. et al. Phase i pharmacokinetic and pharmacodynamic study of the pan-PI3k/mTORC vascular targeted pro-drug SF1126 in patients with advanced solid tumours and b-cell malignancies. Eur. J. Cancer 48, 3319–3327. https://doi.org/10.1016/j.ejca.2012.06.027 (2012).
University of Alabama at Birmingham. Phase IB Trial of LDE225 and Paclitaxel in Recurrent Ovarian Cancer (2014). https://clinicaltrials.gov/ct2/show/NCT02195973 (Accessed October 14, 2021).
Genentech, Inc. A Study of Vismodegib (GDC-0449, Hedgehog Pathway Inhibitor) as Maintenance Therapy in Patients with Ovarian Cancer in a Second or Third Complete Remission (2008). https://clinicaltrials.gov/ct2/show/NCT00739661 (Accessed October 14, 2021).
Subramani, R. et al. Targeting insulin-like growth factor 1 receptor inhibits pancreatic cancer growth and metastasis. PLoS ONE 9, e97016. https://doi.org/10.1371/journal.pone.0097016 (2014).
Ito, H., Gardner-Thorpe, J., Zinner, M. J., Ashley, S. W. & Whang, E. E. Inhibition of tyrosine kinase src suppresses pancreatic cancer invasiveness. Surgery 134, 221–226. https://doi.org/10.1067/msy.2003.224 (2003).
Ferro, R. Emerging role of the KRAS-PDK1 axis in pancreatic cancer. World J. Gastroenterol. 20, 10752. https://doi.org/10.3748/wjg.v20.i31.10752 (2014).
Parsons, C. M., Muilenburg, D., Bowles, T. L., Virudachalam, S. & Bold, R. J. The role of akt activation in the response to chemotherapy in pancreatic cancer. Anticancer Res. 30, 3279–3289 (2010).
Hassan, Z. et al. MTOR inhibitor-based combination therapies for pancreatic cancer. Br. J. Cancer 118, 366–377. https://doi.org/10.1038/bjc.2017.421 (2018).
Li, X., Ding, X. & Adrian, T. E. Arsenic trioxide induces apoptosis in pancreatic cancer cells via changes in cell cycle, caspase activation, and GADD expression. Pancreas 27, 174–179. https://doi.org/10.1097/00006676-200308000-00011 (2003).
University of Chicago. Arsenic Trioxide in Treating Patients with Pancreatic Cancer that has not Responded to Gemcitabine (2003). https://clinicaltrials.gov/ct2/show/NCT00053222 (Accessed October 14, 2021).
Philip, P. A. et al. Dual blockade of epidermal growth factor receptor and insulin-like growth factor receptor-1 signaling in metastatic pancreatic cancer: Phase ib and randomized phase II trial of gemcitabine, erlotinib, and cixutumumab versus gemcitabine plus erlotinib (SWO. Cancer 120, 2980–2985. https://doi.org/10.1002/cncr.28744 (2014).
Pawaskar, D. K. et al. Synergistic interactions between sorafenib and everolimus in pancreatic cancer xenografts in mice. Cancer Chemother. Pharmacol. 71, 1231–1240. https://doi.org/10.1007/s00280-013-2117-x (2013).
Dana-Farber Cancer Institute. RAD001 in Previously Treated Patients with Metastatic Pancreatic Cancer (2006). https://clinicaltrials.gov/ct2/show/NCT00409292 (Accessed October 14, 2021).
Liang Bi, Y., Min, M., Shen, W. & Liu, Y. Genistein induced anticancer effects on pancreatic cancer cell lines involves mitochondrial apoptosis, g 0 /g 1 cell cycle arrest and regulation of STAT3 signalling pathway. Phytomedicine 39, 10–16. https://doi.org/10.1016/j.phymed.2017.12.001 (2018).
Awasthi, N., Hinz, S., Brekken, R. A., Schwarz, M. A. & Schwarz, R. E. Nintedanib, a triple angiokinase inhibitor, enhances cytotoxic therapy response in pancreatic cancer. Cancer Lett. 358, 59–66. https://doi.org/10.1016/j.canlet.2014.12.027 (2015).
University of Texas Southwestern Medical Center. Study of Nintedanib and Chemotherapy for Advanced Pancreatic Cancer (2016). https://clinicaltrials.gov/ct2/show/NCT02902484 (Accessed October 14, 2021).
Mita, M. M. et al. Phase i trial of the novel mammalian target of rapamycin inhibitor deforolimus (AP23573; MK-8669) administered intravenously daily for 5 days every 2 weeks to patients with advanced malignancies. J. Clin. Oncol. 26, 361–367. https://doi.org/10.1200/jco.2007.12.0345 (2008).
Karavasilis, V. et al. Gemcitabine combined with the mTOR inhibitor temsirolimus in patients with locally advanced or metastatic pancreatic cancer. A hellenic cooperative oncology group phase i/II study. Targeted Oncol. 13, 715–724. https://doi.org/10.1007/s11523-018-0605-y (2018).
National Cancer Institute (NCI). CCI-779 in Treating Patients with Locally Advanced or Metastatic Pancreatic Cancer (2004). https://clinicaltrials.gov/ct2/show/NCT00075647 (Accessed October 14, 2021).
Rehan, M. Anticancer compound XL765 as PI3k/mTOR dual inhibitor: A structural insight into the inhibitory mechanism using computational approaches. PLoS One 14, e0219180. https://doi.org/10.1371/journal.pone.0219180 (2019).
Vidri, R. J. & Fitzgerald, T. L. GSK-3: An important kinase in colon and pancreatic cancers. Biochimica et Biophysica Acta (BBA) Mol. Cell Res. 1867, 118626. https://doi.org/10.1016/j.bbamcr.2019.118626 (2020).
Kumarasamy, V., Ruiz, A., Nambiar, R., Witkiewicz, A. K. & Knudsen, E. S. Chemotherapy impacts on the cellular response to CDK4/6 inhibition: Distinct mechanisms of interaction and efficacy in models of pancreatic cancer. Oncogene 39, 1831–1845. https://doi.org/10.1038/s41388-019-1102-1 (2019).
Sonpavde, G., Hutson, T. E. & Sternberg, C. N. Pazopanib, a potent orally administered small-molecule multitargeted tyrosine kinase inhibitor for renal cell carcinoma. Expert Opin. Investig. Drugs 17, 253–261. https://doi.org/10.1517/13543784.17.2.253 (2008).
Iseki, H. A novel strategy for inhibiting growth of human pancreatic cancer cells by blocking cyclin-dependent kinase activity. J. Gastrointest. Surg. 2, 36–43. https://doi.org/10.1016/s1091-255x(98)80101-7 (1998).
Wang, J. & Pendergast, A. M. The emerging role of ABL kinases in solid tumors. Trends Cancer 1, 110–123. https://doi.org/10.1016/j.trecan.2015.07.004 (2015).
Xu, J. et al. PIM-1 contributes to the malignancy of pancreatic cancer and displays diagnostic and prognostic value. J. Exp. Clin. Cancer Res. https://doi.org/10.1186/s13046-016-0406-z (2016).
National Cancer Institute (NCI). Docetaxel and Flavopiridol in Treating Patients with Refractory Metastatic Pancreatic Cancer (2006). https://clinicaltrials.gov/ct2/show/NCT00331682 (Accessed October 14, 2021).
Kazi, A. et al. Global phosphoproteomics reveal CDK suppression as a vulnerability to KRas addiction in pancreatic cancer. Clin. Cancer Res. 27, 4012–4024. https://doi.org/10.1158/1078-0432.ccr-20-4781 (2021).
Isakoff, S. J. et al. Bosutinib plus capecitabine for selected advanced solid tumours: Results of a phase 1 dose-escalation study. Br. J. Cancer 111, 2058–2066. https://doi.org/10.1038/bjc.2014.508 (2014).
Wei, J. et al. Identification of biomarkers and their functions in dasatinib-resistant pancreatic cancer using bioinformatics analysis. Oncol. Lett. https://doi.org/10.3892/ol.2019.10281 (2019).
National Cancer Institute (NCI). Dasatinib in Treating Patients with Metastatic Pancreatic Cancer (2007). https://clinicaltrials.gov/ct2/show/NCT00474812 (Accessed October 14, 2021).
Chen, J. et al. The tyrosine kinase inhibitor imatinib fails to inhibit pancreatic cancer progression. Cancer Lett. 233, 328–337. https://doi.org/10.1016/j.canlet.2005.03.027 (2006).
University of Medicine and Dentistry of New Jersey. Gemcitabine and Imatinib Mesylate as First-Line Therapy in Patients with Locally Adv. or Metastatic Pancreatic Cancer (2005). https://clinicaltrials.gov/ct2/show/NCT00161213 (Accessed October 14, 2021).
Blay, J.-Y. & von Mehren, M. Nilotinib: A novel, selective tyrosine kinase inhibitor. Semin. Oncol. 38, S3–S9. https://doi.org/10.1053/j.seminoncol.2011.01.016 (2011).
Heo, S.-K. et al. The c-abl inhibitor, radotinib induces apoptosis in multiple myeloma cells via mitochondrial-dependent pathway. Sci. Rep. https://doi.org/10.1038/s41598-021-92651-9 (2021).
Stuart Salmon, MD. A Study of Regorafenib in Advanced Pancreatic Cancer Patients (2014). https://clinicaltrials.gov/ct2/show/NCT02080260 (Accessed October 14, 2021).
Aldoss, I. T., Tashi, T. & Ganti, A. K. Seliciclib in malignancies. Expert Opin. Investig. Drugs 18, 1957–1965. https://doi.org/10.1517/13543780903418445 (2009).
Burris, H. A. et al. Umbralisib, a novel PI3k delta and casein kinase-1 epsilon inhibitor, in relapsed or refractory chronic lymphocytic leukaemia and lymphoma: An open-label, phase 1, dose-escalation, first-in-human study. Langet. Oncol. 19, 486–496. https://doi.org/10.1016/s1470-2045(18)30082-2 (2018).
Kang, Y. et al. Efficacy and safety of multiple dosages of fostamatinib in adult patients with rheumatoid arthritis: A systematic review and meta-analysis. Front. Pharmacol. https://doi.org/10.3389/fphar.2019.00897 (2019).
Rigel Pharmaceuticals. Efficacy and Safety Study of Fostamatinib Tablets to Treat B-cell Lymphoma (2007). https://clinicaltrials.gov/ct2/show/NCT00446095 (Accessed October 14, 2021).
Sidney Kimmel Comprehensive Cancer Center at Johns Hopkins. Clinical Trial of Combined Fostamatinib and Paclitaxel in Ovarian Cancer (2017). https://clinicaltrials.gov/ct2/show/NCT03246074 (Accessed October 14, 2021).
Zañudo, J. G. T. & Albert, R. Cell fate reprogramming by control of intracellular network dynamics. PLOS Comput. Biol. 11, e1004193. https://doi.org/10.1371/journal.pcbi.1004193 (2015).
Murrugarra, D., Veliz-Cuba, A., Aguilar, B. & Laubenbacher, R. Identification of control targets in Boolean molecular network models via computational algebra. BMC Syst. Biol. https://doi.org/10.1186/s12918-016-0332-x (2016).
Biane, C. & Delaplace, F. Causal reasoning on Boolean control networks based on abduction: Theory and application to cancer drug discovery. IEEE/ACM Trans. Comput. Biol. Bioinform. 16, 1574–1585. https://doi.org/10.1109/tcbb.2018.2889102 (2019).
Acknowledgements
This work was partially supported by the Academy of Finland (project 311371/-2017 to E.C.) and by the Romanian National Authority for Scientific Research and Innovation (PED Grant 2391 to I.P.).
Author information
Authors and Affiliations
Contributions
V.-B.P., D.I.N., E.C. and I.P. designed the study. V.-B.P. and I.P. performed the computational analysis. V.-B.P. and K.K. collected and curated the data. V.-B.P., E.C. and I.P. analyzed the results and co-wrote the manuscript. All authors were involved in drafting the article and all have reviewed and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Popescu, VB., Kanhaiya, K., Năstac, D.I. et al. Network controllability solutions for computational drug repurposing using genetic algorithms. Sci Rep 12, 1437 (2022). https://doi.org/10.1038/s41598-022-05335-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-05335-3
This article is cited by
-
Systems biology approaches to identify driver genes and drug combinations for treating COVID-19
Scientific Reports (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.