Abstract
Vaccines are thought to be the best available solution for controlling the ongoing SARS-CoV-2 pandemic. However, the emergence of vaccine-resistant strains may come too rapidly for current vaccine developments to alleviate the health, economic and social consequences of the pandemic. To quantify and characterize the risk of such a scenario, we created a SIR-derived model with initial stochastic dynamics of the vaccine-resistant strain to study the probability of its emergence and establishment. Using parameters realistically resembling SARS-CoV-2 transmission, we model a wave-like pattern of the pandemic and consider the impact of the rate of vaccination and the strength of non-pharmaceutical intervention measures on the probability of emergence of a resistant strain. As expected, we found that a fast rate of vaccination decreases the probability of emergence of a resistant strain. Counterintuitively, when a relaxation of non-pharmaceutical interventions happened at a time when most individuals of the population have already been vaccinated the probability of emergence of a resistant strain was greatly increased. Consequently, we show that a period of transmission reduction close to the end of the vaccination campaign can substantially reduce the probability of resistant strain establishment. Our results suggest that policymakers and individuals should consider maintaining non-pharmaceutical interventions and transmission-reducing behaviours throughout the entire vaccination period.
Similar content being viewed by others
Introduction
Vaccines are among the most effective public health measures against infectious disease1. Their track record brings hope that SARS-CoV-2 may soon be under control2 as a consequence of a plethora of vaccine development efforts3,4,5,6,7,8. A potential cause of concern is the low rate of vaccine production and administration9 coupled with reports of new strains with higher transmission rates10,11,12 and even with potential for some degree of vaccine resistance13,14,15,16. A number of models considered the dynamics of the spread of a vaccine-resistant strain in the population17,18,19,20. However, to our knowledge, the interplay of the population vaccination rate with the stochastic dynamics of emergence of a resistant strain has been discussed21, but not formally modeled. Specifically, a concern is whether a combination of vaccination and transmission rates can create positive selection pressure on the emergence and establishment of resistant strains22,23. To address this issue, we implemented a model to simulate the probability of emergence of a resistant strain as a function of vaccination rates and changes in the rate of virus transmission, resembling those caused by non-pharmaceutical interventions and behavioural changes. We then performed a number of simulations based on realistic parameters to study the likelihood and pattern of the emergence of a resistant strain. Finally, we considered possible countermeasures to reduce the probability of the establishment of the resistant strain in the population.
Results
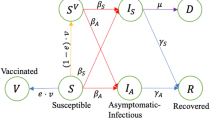
We implemented a modification of a SIR model18,24 that included additional states to study the interplay of the rate of vaccination, rate of transmission and the likelihood of emergence of resistant strains (Fig. 1a). In addition to other states, individuals could be vaccinated (V), infected by the resistant strain (Ir), or simultaneously be vaccinated and infected with the resistant strain (IrV). The model was run to simulate a population of 10,000,000 individuals over 3 years with the vaccination starting after the first year. In the model, the susceptible individuals (S) are infected by the wildtype, or the original, strain at a rate of β and infected individuals recover at a rate of γ or die at a rate of δ. At each time step, a fraction θ of all non-infected individuals is vaccinated and with some fixed probability p, an infected individual becomes infected with a resistant strain. Conversely, any individual infected with the resistant strain can revert back to the wildtype strain population with the same probability, p. Immunity acquired after infection decayed at a rate of μ. Overall, our model included eight character states and six transition parameters between them (Fig. 1a, Table 1).
The states, transition parameters and dynamics. (a) States are shown in circles and transition parameters in squares. The transition parameter, μ, is the rate at which individuals lose natural immunity and p, is the probability that an individual infected with the wildtype strain transmits a resistant strain, so it is not a deterministic parameter. Example dynamics of the number of individuals infected with the wildtype (blue) and resistant strains (red) for p = 10–6, θ0 = 1/365 and Fh = 15,000. The period of vaccination is highlighted (green). Under the same parameters the resistant strain may emerge and go extinct, (b), or become established, (c).
The rate of transmission in the course of a pandemic is typically cyclical34,35,36 due to government interventions36,37, behavioural changes38,39,40, and environmental41,42 and other factors43,44. Generally, the number of infected individuals is wave-like, guided by periods of high rate of transmission, followed by periods of a low rate of transmission31,34,35,45. We thus varied β, the rate of virus transmission to reflect this cyclical behavior (Fig. 1b,c). A high rate of transmission (βh = 0.18, equivalent to the effective reproduction number of Rh = 2.52) was alternated with a low rate (βl = 0.055 or Rl = 0.77), which broadly reflected the observed rates of transmission in various countries affected by the SARS-CoV-19 pandemic with and without lockdown measures, respectively31,32,33. The low rate of transmission was triggered in the model when the number of individuals infected with any strain reached a high threshold Fh = (Iwt + Ir + IrV). We considered two modes of transition from a low rate of transmission back to a high rate, when the number of infected individuals reached a low threshold Fl at a constant value of Fl = (Iwt + Ir + IrV) = 1000, which was used to generate the main figures, and at a relative value of Fl = Fh/8, which are available as “Supplementary materials S1”. The explored values of Fh and Fl were selected such that the number of infection waves during the first year of the model roughly coincided with the number of waves of SARS-CoV-2 infection observed in most countries during the first year of the pandemic.
SIR-like models frequently consider only deterministic dynamics18. However, the emergence of a new strain is an inherently stochastic process under extensive influence of genetic drift46,47. Therefore, we incorporated a stochastic stage into our model to allow for genetic drift in the early phases of population dynamics of the resistant strains. The growth rate of the number of individuals infected with the wildtype strain at time t was determined deterministically by (β*S/N − γ − δ)Iwt. By contrast, when the frequency of the resistant strain in the population is low, the number of transmissions of the resistant strain was drawn from a Poisson distribution with a mean of \((\beta {I}_{r}(S+V)/N)dt\)48. However, when the frequency of the resistant strain is greater than 1000 individuals (0.01% of the population), making it highly unlikely to disappear by stochastic forces, the dynamics are treated deterministically in the same manner as the wildtype strain.
We define three stages of vaccine-resistant strain propagation, including emergence, the appearance of the first individual with the infected strain, establishment, the time point when the number of infected individuals reached 1000, and extinction, when the number of resistant strain infected individuals returned to zero. The impact of three parameters on the resistant strain propagation were explored: the probability of the emergence of the resistant strain (p), the speed of vaccination (θ) and the initiation of periods of lower rate of transmission (Fh). All other parameters were constants and their values were chosen to be broadly reflecting a realistic set of parameters that approximate the available data for the SARS-CoV-2 pandemic, μ = 1/180, γ = 0.99*1/14 and δ = 0.01*1/14 (see Table 1).
Higher probability of the initial emergence of a resistant strain emerging in a single individual, p, had a predictably49 positive effect on the probability of the establishment of the resistant strain (Figs. S1), but depended on the rate of vaccination (θ) and low transmission initiation (Fh) in a complex manner (Fig. 2, Figs. S1). The dependency was periodic and the probability of establishment of the resistant strain was different by a factor of two even for some similar values of θ and Fh (Fig. 2d,e).
Impact of the rate of vaccination, θ, and the initiation of low rate of transmission, Fh, on model dynamics. The cumulative death rate from the (a) wildtype and (b) resistant strains, (c) the number of wildtype-strain infected individuals at tv60, the point in time when 60% of the population is vaccinated and (d) the probability of resistant strain establishment, for p = 10–6. (e) The probability of emergence of the resistant strain as a function of the probability of emergence, p shown for the parameter ranges of θ and Fh in the corresponding red and blue boxes from figure (d). (f) The average number of times of 8 × 106 simulation runs during which a resistant strain emerges (black) or goes extinct (grey) during periods of low (βl) or high (βh) transmission for p = 10–6. (g) A resistant strain was never observed to establish during periods of low transmission (βl) for p = 10–6.
The behaviour of the emergence, establishment and extinction of the resistant strain in the population bears striking resemblance to the population genetics problem addressing the survival of a beneficial allele in a growing population50,51. To understand the stochastic dynamics of the resistant strain in the model, it is therefore instructive to consider the underlying mechanism in population genetics terms. Unless the rate of mutation is zero, or infinitesimally low, new variants will emerge in the population at a rate of p*Iwt. When the rates of transmission of the wildtype and the resistant strain are equal, the probability that the resistant strain will go extinct, 1 − Qt, can be approximated by
where s is the selection advantage of the resistant strain46,52 and Rtr = (S + V)β/N(γ + δ), or the rate of population growth. Therefore, even when there is no selective advantage of the resistant strain (s = 0) over the wildtype strain but the rate of transmission is high (Rtr > 1), the likelihood that a new mutation is lost from the population is small (~ 10% for βh = 0.18, or R0 = 2.52). By contrast, when the rate of transmission is low (Rtr < 1, which is the case during the low transmission periods in the model), the probability of extinction of the resistant strain by genetic drift is substantial46,47. The results of our model are consistent with theory46,47, such that the resistant strain emerges during periods of high and low transmission rates, but goes extinct with higher probability during periods of low transmission (Fig. 2f). Furthermore, under the parameters of our model the resistant strain becomes established only when the rate of transmission is high (Fig. 2f).
The complex influence of the speed of vaccination, θ, and initiation of low transmission period, Fh, on the dynamics of establishment of the resistant strain (Fig. 2d) is, therefore, likely driven by the overlap of the vaccination period and the periodicity of the cycles of the number of infected individuals driven by the interaction of Fh and θ (Fig. 1b,c). The coincidence of a high number of vaccinated individuals and a high rate of transmission has two effects on the resistant strain. First, as mentioned previously, because the rate of transmission is high, the emerging resistant strain is not lost through genetic drift (see also50,53). Second, a high number of vaccinations creates a selective advantage of the resistant strain over the wildtype strain23. The effective reproductive number of the wildtype versus the resistant strains, Rtwt/Rtr, is (V + S)/S, which is the selective advantage 1 + s in Eq. (1). Thus, when V is large the resistant strain has a growth advantage over the wildtype strain, contributing to its establishment in the population towards the end of the vaccination campaign. Taken together, the highest probability for establishment of the resistant strain for a given p is reached when V, Iwt and β (and the corresponding Rtr) are large (Fig. 2c, Eq. (1)).
Indeed, when p = 10–6, in those cases when the resistant strain becomes established, its initial time of emergence frequently occurs at around the time when 60% of the population is vaccinated (Fig. 3). Therefore, we then tested the influence of a single intervention triggering at a single extraordinary period of low transmission centred around 60% of vaccinated individuals in the population (Fig. 3). We varied the duration of this intervention, T, ranging from 1 week to 120 days and considered three rates of transmission, βl = 0.055 (R0 = 0.77), 0.03 (R0 = 0.42) and 0.01 (R0 = 0.14). Both parameters decrease the probability of establishment of the resistant strain with the length of the intervention having a relatively stronger effect (Fig. 3, Figs. S1, S1, S1, S1, S1, S1, S1).
Time of initial emergence of a resistant strain that has become established. Probability density that the resistant strain emerges as a function of time since the start of the simulation, t, rescaled by the time at which 60% of the individuals are vaccinated, tV60, averaged across simulations with θ (0.001 through 0.015), Fh (2000 through 20,000) and p = 10–6. Without any extraordinary periods of low transmission (blue line) the peak of the likelihood of emergence of a new strain is at t/tV60 = 1. The likelihood of emergence of a resistant strain can be reduced by an extraordinary period of low transmission centered at t/tV60 = 1 with a stronger reduction when such period is longer, T (colour-coded), or when the rate of transmission is more strongly reduced (a) βl = 0.055, (b) βl = 0.03, (c) βl = 0.01.
Discussion
Our model suggests three specific risk factors that favour the emergence and establishment of a vaccine-resistant strain that are intuitively obvious: high probability of initial emergence of the resistant strain, high number of infected individuals54 and low rate of vaccination55. By contrast, a counterintuitive result of our analysis is that the highest risk of resistant strain establishment occurs when a large fraction of the population has already been vaccinated but the transmission is not controlled. Similar conclusions have been reached in a SIR model of the ongoing pandemic56 and a model of pathogen escape from host immunity57. Furthermore, empirical data consistent with this result has been reported for influenza58. Indeed, it seems likely that when a large fraction of the population is vaccinated, especially the high-risk fraction of the population (aged individuals and those with specific underlying conditions) policy makers and individuals will be driven to return to pre-pandemic guidelines59 and behaviours conducive to a high rate of virus transmission60,61. However, the establishment of a resistant strain at that time may lead to serial rounds of resistant strain evolution with vaccine development playing catch up in the evolutionary arms race against novel strains.
Prior to discussion of the implications of our model we reflect on several properties of the assumptions and implementation of our model. In classical SIR-like deterministic models even a single individual infected with a vaccine resistant strain with reproduction number Rt > 1 will lead to automatic establishment of the strain in the population. In an analytical solution, a SIR-like model, even for Rt < 1 for the vaccine resistant strain, the number of infected individuals will tend to 0 but only as time tends to infinity. In actual populations, a single individual infected with a vaccine resistant strain still has a non-negligible chance not to infect anyone causing the variant to go extinct due to random stochastic forces47. Therefore, the implementation of stochastic dynamics62,63 of the vaccine resistant strain at low frequency in our model, considers the impact of random drift on its dynamics, which lies at the heart of extinction of rare strains.
We considered the dynamics of a single vaccine resistant strain, however, there may be different mutations that can lead to vaccine resistance. The emergence of different genotypes causing the same phenotype is analogous to a distinction in population genetics between alleles identical by state and by descent64. In our model, the treatment of independent emergence of different mutations as a single entity does not influence the dynamics under the following two assumptions. First, that different mutations lead to exactly the same phenotype, which is vaccine resistance, and, second, that there is no recombination. However, the reported dynamics may be quantitatively different if either of the two assumptions do not hold.
We have not explored the parameter ranges of βh, βl, the high and low rates of transmission, respectively, and Fl the threshold between low and high rate of transmission. We selected the βh and βl, to represent the known transmission values at the start of the pandemic31,32,33. However, evolving strains are reported to have a higher rate of transmission10 leading to higher βh and, possibly, βl values than we used. An increase in the rate of transmission is not expected to qualitatively influence the reported dynamics, but would shift the probability density of establishment of a resistant strain (Fig. 3). Indeed, the peak probability at 60% vaccinated individuals roughly corresponds to the point at which for the given βh, Rt, the average number of transmissions for one infected individual, becomes less than 1. Because the reproduction number for the vaccine resistant strain, Rt, is equal to (S + V)β/N(γ + δ), the perk of the risk of establishment of the vaccine resistant strain would increase proportional to an increase of β. An increase in either Fh or Fl would lead to more individuals becoming infected and a proportionally higher rate of emergence of the vaccine related strain, but would not change the qualitative behaviour of the model. Furthermore, an increase of Fl would lead to reversion to a high transmission rate with higher number of infected individuals, leading to shorter periods of low transmission and decreased probability of extinction of the vaccine resistant strains.
The results of our model provide several qualitative implications for the strategy forward in the months of vaccination. In our model, the probability of emergence of a resistant strain in one individual per day was in the range of 10–5 to 10–8 for a population of 107 individuals. For the entire human population of ~ 1010 that probability would be 10–8 to 10–11, which does not seem improbably large. As of February 2021, ~ 109 individuals have been infected by SARS-CoV-265 with an average 14 days of sickness per individual25, so > 1010 number of total days of infected individuals. Furthermore, highly mutated strains may emerge as a result of long shedding in immunocompromised individuals, a rare but realistic scenario66,67,68. Taken together, the emergence of a partially or fully vaccine-resistant strain and its eventual establishment appears inevitable. However, as vaccination needs to be ahead of the spread of such strains in similar ways to influenza23, it is necessary to reduce the probability of establishment by a targeted effort to reduce the virus transmission rate towards the end of the vaccination period before the current vaccines become ineffective. Conversely, lack of non-pharmaceutical interventions at that time can increase the probability of establishment of vaccine-resistant strains. For example, plans to vaccinate individuals with a high risk of a fatal disease outcome followed by a drive to reach herd immunity while in uncontrolled transmission among the rest of the population is likely to greatly increase the probability that a resistant strain is established, annulling the initial vaccination effort. Another potential risk factor may be the reversion of vaccinated individuals to pre-pandemic behaviours that can drive the initial spread of the resistant strain.
One simple specific recommendation is to keep transmission low even when a large fraction of the population has been vaccinated by implementing acute non-pharmaceutical interventions (i.e. strict adherence to social distancing) for a reasonable period of time, to allow emergent lineages of resistant strains to go extinct through stochastic genetic drift. The implementation of non-pharmaceutical measures at a time of high vaccination can also help reduce infectivity when the efficacy of vaccines is not perfect69. Additional factors that may make these measures even more effective are: (1) increased and widespread testing, (2) rigorous contact tracing, (3) high rate of viral sequencing of positive cases58,70 and (4) travel restrictions. Finally, while our model formally considers only one homogenous population, our data also suggest that delays in vaccination in some countries relative to others will make the global emergence of a vaccine-resistant strain more likely. Without global coordination, vaccine resistant strains may be eliminated in some populations but could persist in others. Thus, a truly global vaccination effort may be necessary to reduce the chances of a global spread of a resistant strain.
Materials and methods
Our extension of the SIR Model features 8 distinct states. Susceptible, S, and recovered, R, individuals are vaccinated over time to become vaccinated, V, or recovered vaccinated, RV, respectively. Susceptible individuals can become infected with the wildtype, Iwt, or the resistant virus strain, Ir. While the vaccinated population is immune to the wildtype, it can be infected by the vaccine-resistant strain, in which case the state is represented by IrV. After a while any infected individual recovers or dies, D. Finally, we assume that the recovered population retains natural immunity towards both strains, but becomes susceptible again with some small rate, μ. In our model, immunity against the wildtype strain gained through vaccination is not lost during the entire model period of 3 years, consistent with current estimates71,72.
The total number of individuals, N, in the population remains constant at 10,000,000, which includes the diseased individuals. We do not introduce new individuals into the population because only a very small number of individuals die during the 3 years that we simulate.
For all of the eight states, for convenience we omit the time index, e.g. we write, for example, S instead of S(t). In the limit of large population sizes, the full dynamics without mutations can be described by the following set of differential equations. In these equations, \(\dot{x}= dx/dt\) where t is time.
Or, in the matrix format, \(\dot{X}=\widehat{P}X,\) with \(X={(S,{I}_{wt},{I}_{r},{I}_{r}^{V},R,{R}^{V},D,V)}^{T}\)
The dynamics are influenced by the following constant parameters: the recovery rate, γ, the death rate, δ, and the rate at which natural immunity is lost, μ. Additionally we introduce a time dependent transmission rate \(\beta (t)\) and a function \(\theta (t)\), which controls the speed of vaccination.
Time dependent transmission rate
Pandemics often proceed in a wave-like pattern31,34,35,45, so we introduce a parameter \(\beta (t)\), which switches between high and low transmission rates. The model begins with a period of a high rate of transmission, \({\beta }_{h}/N.\) A low transmission rate, \({\beta }_{l}/N\), is initiated when the fraction of individuals infected with any strain, \(I=({I}_{wt}+{I}_{r}+{I}_{r}^{V})\), reaches the value of Fh. Transition from a period of low to high infection rate occurs at Fl = 1000 or Fl = Fh/8.
Vaccination
Vaccination is modelled as almost always a linear function with saturation. The deviation from linearity occurs towards the end of the vaccination period. At that time, there may be fewer individuals that can be vaccinated than the number of individuals vaccinated at any time point, or \(S + R - h < \theta\). This state can persist for longer than one point in time because in our model infected individuals are vaccinated only once they recover. h denotes the number of individuals in the population that are never vaccinated. A maximum of N − h individuals can be vaccinated at the end of the vaccination program. The constant k controls the saturation of the vaccination speed once the number of susceptible individuals is significantly depleted. The state dependent vaccination speed \(\theta (t)\) is given as:
where \({\theta }_{0}\) can take different values and h and k are chosen to be small (see Table 1).
Integration method
The deterministic differential equations Eq. (11) were numerically solved using an Euler Forward Integration Scheme, with time step Δt, measured in days.
Resistant strain
Each day and for every individual infected with the wildtype strain, Iwt, there is a small probability p, that a vaccine-resistant strain emerges in that individual. Then this individual switches from state Iwt to state Ir. Conversely, any individual infected with the resistant strain, Ir can revert back to the wildtype strain, Iwt, with the same probability p. Each time step the number of individuals that transition between being infected with different strains is drawn from a Poisson distribution with mean ΔtpIwt, for transition to the resistant strain, or ΔtpIr, for reversion to the wildtype strain. The sum of Poisson distributed random variables is itself a Poisson distributed random variable with the mean corresponding to the sum of the means.
Stochastic and deterministic regimes
The population dynamics of a rare variant is an inherently stochastic process46,47. We can formally treat the spread of a disease in our model as a stochastic birth–death process. In the following we illustrate this with the number of wildtype infections Iwt as an example. In each infinitesimally small time step dt, there is a probability \(\beta S{I}_{wt}dt\), that the wildtype population Iwt grows by 1, \({I}_{wt}\to {I}_{wt}+1,\) Iw while the susceptible population is decreased, \(S\to S-1\). Similarly, with probability \((\gamma +\delta ){I}_{wt}dt,\) Iwt is reduced by 1, \({I}_{wt}\to {I}_{wt}-1\), while the number of recovered or dead grows by 1. We carefully model small populations, \({I}_{wt}<{N}^{*}\), with \({N}^{*}\) representing a small number of individuals, using a stochastic Tau-Leaping Algorithm73. We choose a fixed time step size τ, that is equal to the time step of the Euler Integrator Δt. For very small Iwt Tau Leaping Algorithm can produce a negative population73. This stems from the fact, that the number of events K that occur in time τ is drawn from a Poisson Distribution, that always assigns a non-zero probability for any \(K>{I}_{wt}\). We reduce the chances of such a scenario, by solving the exact SSA Gillespie Algorithm when Iwt is below a critical size Nc48.
For large Iwt, larger than some N*, this stochastic process can be approximated with the limiting differential Eq. (4) and an Euler Integration Scheme. Once \({I}_{wt}\ge {N}^{*}\), we consider that the resistant strain of the virus is established in the population and we continue modelling it using the deterministic equation18.
Parallel evaluation of deterministic and stochastic variables
In our model we evaluate deterministic and the stochastic dynamics in parallel. While small populations of infected individuals are treated as stochastic, other variables, such as the number of susceptible individuals, S, are evaluated within the deterministic regime. While the infection numbers of the wildtype or the emergent strain are in the stochastic regime (< N*), the corresponding terms that contain the wildtype infections Iwt or the emergent infections Ir and IrV are removed from the deterministic rate equations. When Iwt or Ir + IrV grow above the threshold value N*, the corresponding population of infected individuals is treated as deterministic.
Sources of errors
Finally, we discuss some sources of errors in our simulation: (1) depending on the time step Δt the Euler Integration Scheme is not exact. In most of our simulations, we choose a time step of 1 day, Δt = 1d. (2) Using the deterministic rate equations for the infection numbers in Eq. (11) is an approximation to the exact stochastic dynamics given by a birth–death model. The quality of this approximation is given by the threshold value N*, which was 1000 in our model. (3) When Iwt or Ir + IrV trespasses the threshold N* from above, the populations of infected individuals changes from being treated as a real number (the mean field average) to being treated as a natural number. We truncate the mean field average with a floor function and treat the remainder as part of the recovered population. (4) The Tau Leaping algorithm is an approximation to the exact SSA Gillespie Algorithm, that allows faster evaluation with a constant step size τ. Increasing the threshold value Nc increases the accuracy of the model (Fig. S1). (5) As discussed above, on rare occasions a population of infected individuals drops below 0 in one leap. If this happens we redraw from the same Poisson distribution. (6) Finally, while the time step of the deterministic model Δt and τ are chosen to be equal, for population sizes above Nc, the SSA algorithm acts on exponentially distributed waiting times τSSA between reactions48. This introduces errors, if \({\tau }_{SSA}\gg \Delta t\), because the interaction rates may change, while we wait for the next reaction to occur.
In order to determine a range of acceptable values of Nc, we ran our simulation for a period of T = 200 days, initially loading the system with Iwt = 200 wildtype carriers. For multiple values of Nc and no mutations, we compared the results of disease survival with the analytical solution derived for the birth death process,
We pick Nc = 100 individuals, which gives us a reasonably small error.
Assumptions and choice of parameters
The model is run for a total time of 3 years, with vaccination starting 1 year into the model. We assume that the wildtype and emergent strains have the same infectivity (β is the same for both strains). We assume that infection by any one strain provides immunity to both, reflecting that many vaccines carry only the Spike protein of the SARS-CoV-2 virus and it may be easier to escape immunity provided by the vaccine than the immunity provided by infection. We also assume that the immune response provided by the vaccine is more permanent and that immunity provided by infection, is lost at rate μ, on average after 0.5 years2,71,72,74 after recovery. Both of these assumptions influence the model when the number of infected individuals becomes large, which is unlikely for realistic average rates of transmission across the simulated time.
We assume that susceptible and recovered individuals have an equal chance to be vaccinated, θ0. We also assume that the infection-recovery rate, γ, and infection-fatality rate, δ are the same for the wildtype and mutated strains.
We regulate the rates of transmission exogenously in the model, with the rate of transmission (β) switching between a high rate, βh and a low rate, βl, when the total number of individuals infected with either strain reaches a threshold parameter. These threshold parameters, Fh and Fl, simultaneously reflect the impact of all non-pharmaceutical interventions and behavioural changes of individuals. The ranges of these parameters were chosen to broadly reflect realistic parameters of a pandemic, including rates of infection and several waves of high infection in the first couple of years of the model.
We operate under the assumption that vaccine efficacy not only impacts disease manifestation but also blocks transmission at the same rate, which is a reasonable assumption based on previous vaccine performance but has not yet been demonstrated.
In Table 1 we present the choice of parameters for the model, the ones that were constant and those that were varied, including their boundaries.
Code availability
References
Andre, F. E. et al. Vaccination greatly reduces disease, disability, death and inequity worldwide. Bull. World Health Organ. 86, 140–146 (2008).
Anderson, R. M., Vegvari, C., Truscott, J. & Collyer, B. S. Challenges in creating herd immunity to SARS-CoV-2 infection by mass vaccination. Lancet 396, 1614–1616 (2020).
Polack, F. P. et al. Safety and efficacy of the BNT162b2 mRNA COVID-19 vaccine. N. Engl. J. Med. 383, 2603–2615 (2020).
Logunov, D. Y. et al. Safety and efficacy of an rAd26 and rAd5 vector-based heterologous prime-boost COVID-19 vaccine: An interim analysis of a randomised controlled phase 3 trial in Russia. Lancet https://doi.org/10.1016/s0140-6736(21)00234-8 (2021).
Baden, L. R. et al. Efficacy and safety of the mRNA-1273 SARS-CoV-2 vaccine. N. Engl. J. Med. 384, 403–416 (2021).
Dong, Y. et al. A systematic review of SARS-CoV-2 vaccine candidates. Signal Transduct. Target Ther. 5, 237 (2020).
Graham, B. S. Rapid COVID-19 vaccine development. Science 368, 945–946 (2020).
Malone, B. et al. Artificial intelligence predicts the immunogenic landscape of SARS-CoV-2 leading to universal blueprints for vaccine designs. Sci. Rep. 10, 22375 (2020).
Coronavirus (COVID-19) Vaccinations. Ourworldindata https://ourworldindata.org/covid-vaccinations (2021)
Davies, N. G. et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science 372 https://doi.org/10.1126/science.abg3055 (2021)
Tegally, H. et al. Sixteen novel lineages of SARS-CoV-2 in South Africa. Nat. Med. https://doi.org/10.1038/s41591-021-01255-3 (2021).
Faria, N. R,. et al. Genomics and epidemiology of the P.1 SARS-CoV-2 lineage in Manaus, Brazil. Science 372, 815-821 https://doi.org/10.1126/science.abh2644 (2021).
Cele, S. et al. Escape of SARS-CoV-2 501Y.V2 from neutralization by convalescent plasma. Nature 593, 142-146 https://doi.org/10.1038/s41586-021-03471-w (2021).
Andreano, E. et al. SARS-CoV-2 escape in vitro from a highly neutralizing COVID-19 convalescent plasma. bioRxiv https://doi.org/10.1101/2020.12.28.424451 (2020).
Williams, T. C. & Burgers, W. A. SARS-CoV-2 evolution and vaccines: Cause for concern?. Lancet Respir. Med. https://doi.org/10.1016/S2213-2600(21)00075-8 (2021).
Barnes, C. O. et al. SARS-CoV-2 neutralizing antibody structures inform therapeutic strategies. Nature 588, 682–687 (2020).
Luong, T. H. Mathematical Modeling of Vaccinations: Modified SIR Model, Vaccination Effects, and Herd Immunity (Portland State University, 2019). https://doi.org/10.15760/honors.712.
Huppert, A. & Katriel, G. Mathematical modelling and prediction in infectious disease epidemiology. Clin. Microbiol. Infect. 19, 999–1005 (2013).
Fudolig, M. & Howard, R. The local stability of a modified multi-strain SIR model for emerging viral strains. PLoS ONE 15, e0243408 (2020).
Xiao, Y. & Moghadas, S. M. Impact of viral drift on vaccination dynamics and patterns of seasonal influenza. BMC Infect. Dis. 13, 589 (2013).
Volz, E. M. & Didelot, X. Modeling the growth and decline of pathogen effective population size provides insight into epidemic dynamics and drivers of antimicrobial resistance. Syst. Biol. 67, 719–728 (2018).
Rauff, D., Strydom, C. & Abolnik, C. Evolutionary consequences of a decade of vaccination against subtype H6N2 influenza. Virology 498, 226–239 (2016).
Grenfell, B. T. et al. Unifying the epidemiological and evolutionary dynamics of pathogens. Science 303, 327–332 (2004).
Bjørnstad, O. N., Shea, K., Krzywinski, M. & Altman, N. Modeling infectious epidemics. Nat. Methods 17, 455–456 (2020).
Lauer, S. A. et al. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: Estimation and application. Ann. Intern. Med. 172, 577–582 (2020).
Petersen, E. et al. Comparing SARS-CoV-2 with SARS-CoV and influenza pandemics. Lancet Infect. Dis. 20, e238–e244 (2020).
Yang, W. et al. Estimating the infection-fatality risk of SARS-CoV-2 in New York City during the spring 2020 pandemic wave: A model-based analysis. Lancet Infect. Dis. 21, 203–212 (2021).
Pastor-Barriuso, R. et al. Infection fatality risk for SARS-CoV-2 in community dwelling population of Spain: Nationwide seroepidemiological study. BMJ 371, m4509 (2020).
Hartley, G. E. et al. Rapid generation of durable B cell memory to SARS-CoV-2 spike and nucleocapsid proteins in COVID-19 and convalescence. Sci. Immunol. 5, https://doi.org/10.1126/sciimmunol.abf8891 (2020).
Choe, P. G. et al. Antibody responses 8 months after asymptomatic or mild SARS-CoV-2 infection. Emerg. Infect. Dis. 27, 928-931 https://doi.org/10.3201/eid2703.204543 (2020).
Chowdhury, R. et al. Dynamic interventions to control COVID-19 pandemic: A multivariate prediction modelling study comparing 16 worldwide countries. Eur. J. Epidemiol. 35, 389–399 (2020).
Hilton, J. & Keeling, M. J. Estimation of country-level basic reproductive ratios for novel Coronavirus (SARS-CoV-2/COVID-19) using synthetic contact matrices. PLoS Comput. Biol. 16, e1008031 (2020).
Alimohamadi, Y., Taghdir, M. & Sepandi, M. Estimate of the basic reproduction number for COVID-19: A systematic review and meta-analysis. J. Prev. Med. Public Health 53, 151–157 (2020).
Bjørnstad, O. N. & Viboud, C. Timing and periodicity of influenza epidemics. Proc. Natl. Acad. Sci. USA 113, 12899–12901 (2016).
Martinez, M. E. The calendar of epidemics: Seasonal cycles of infectious diseases. PLoS Pathog. 14, e1007327 (2018).
Kissler, S. M., Tedijanto, C., Goldstein, E., Grad, Y. H. & Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 368, 860–868 (2020).
Habersaat, K. B. et al. Ten considerations for effectively managing the COVID-19 transition. Nat. Hum. Behav. 4, 677–687 (2020).
Althouse, B. M. & Hébert-Dufresne, L. Epidemic cycles driven by host behaviour. J. R. Soc. Interface 11, 20140575 https://doi.org/10.1098/rsif.2014.0575 (2014).
West, R., Michie, S., Rubin, G. J. & Amlôt, R. Applying principles of behaviour change to reduce SARS-CoV-2 transmission. Nat. Hum. Behav. 4, 451–459 (2020).
Van Bavel, J. J. et al. Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 4, 460–471 (2020).
Mecenas, P., Bastos, R. T. R. M., Vallinoto, A. C. R. & Normando, D. Effects of temperature and humidity on the spread of COVID-19: A systematic review. PLoS ONE 15, e0238339 (2020).
Carleton, T., Cornetet, J., Huybers, P., Meng, K. C. & Proctor, J. Global evidence for ultraviolet radiation decreasing COVID-19 growth rates. Proc. Natl. Acad. Sci. USA. 118, e2012370118 https://doi.org/10.1073/pnas.2012370118 (2021).
Rosenstrom, E. et al. High-quality masks reduce COVID-19 infections and deaths in the US. medRxiv https://doi.org/10.1101/2020.09.27.20199737 (2021).
Aleta, A. et al. Modeling the impact of social distancing, testing, contact tracing and household quarantine on second-wave scenarios of the COVID-19 epidemic. medRxiv https://doi.org/10.1101/2020.05.06.20092841 (2020).
Cacciapaglia, G., Cot, C. & Sannino, F. Second wave COVID-19 pandemics in Europe: A temporal playbook. Sci. Rep. 10, 15514 (2020).
Charlesworth, B. & Charlesworth, D. Elements of Evolutionary Genetics (Roberts & Company, 2010).
Haldane, J. B. S. A mathematical theory of natural and artificial selection, part V: Selection and mutation. Math. Proc. Cambridge Philos. Soc. 23, 838–844 (1927).
Gillespie, D. T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115, 1716–1733 (2001).
Elena, S. F. & Sanjuán, R. Adaptive value of high mutation rates of RNA viruses: Separating causes from consequences. J. Virol. 79, 11555–11558 (2005).
Uecker, H. & Hermisson, J. On the fixation process of a beneficial mutation in a variable environment. Genetics 188, 915–930 (2011).
Eshel, I. On the survival probability of a slightly advantageous mutant gene in a multitype population: A multidimensional branching process model. J. Math. Biol. 19, 201–209 (1984).
Otto, S. P. & Whitlock, M. C. The probability of fixation in populations of changing size. Genetics 146, 723–733 (1997).
Orr, H. A. & Unckless, R. L. Population extinction and the genetics of adaptation. Am. Nat. 172, 160–169 (2008).
Boni, M. F., Gog, J. R., Andreasen, V. & Christiansen, F. B. Influenza drift and epidemic size: The race between generating and escaping immunity. Theor. Popul. Biol. 65, 179–191 (2004).
Wen, F. T., Malani, A. & Cobey, S. The beneficial effects of vaccination on the evolution of seasonal influenza. biorxiv https://doi.org/10.1101/162545.
Rochman, N., Wolf, Y. & Koonin, E. Substantial impact of post-vaccination contacts on cumulative infections during viral epidemics. F1000Res 10, 315 (2021).
Chabas, H. et al. Evolutionary emergence of infectious diseases in heterogeneous host populations. PLoS Biol. 16, e2006738 (2018).
Boni, M. F. Vaccination and antigenic drift in influenza. Vaccine 26(Suppl 3), C8-14 (2008).
Eichenbaum, M. S., Rebelo, S. & Trabandt, M. The Macroeconomics of Epidemics. Working Paper Series https://doi.org/10.3386/w26882(2020).
Flaxman, S. et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 584, 257–261 (2020).
Dickens, B. L. et al. Modelling lockdown and exit strategies for COVID-19 in Singapore. Lancet Regional Health Western Pacific 1, 100004 https://doi.org/10.1016/j.lanwpc.2020.100004 (2020).
Adak, D., Majumder, A. & Bairagi, N. Mathematical perspective of COVID-19 pandemic: Disease extinction criteria in deterministic and stochastic models. Chaos Solitons Fractals 142, 110381 (2021).
Khatri, B. S. Stochastic extinction of epidemics: how long would it take for Sars-Cov-2 to die out without herd immunity? medRxiv https://doi.org/10.1101/2020.08.10.20171454 (2020).
Gillespie, J. H. Population Genetics: A Concise Guide (JHU Press, 2004).
Dong, E., Du, H., Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 20, 533-534 https://doi.org/10.1016/S1473-3099(20)30120-1(2020).
Avanzato, V. A. et al. Case study: Prolonged infectious SARS-CoV-2 shedding from an asymptomatic immunocompromised individual with cancer. Cell 183, 1901-1912.e9 (2020).
Choi, B. et al. Persistence and evolution of SARS-CoV-2 in an immunocompromised host. N. Engl. J. Med. 383, 2291–2293 (2020).
Bazykin, G.A., Stanevich, O., Danilenko, D., Fadeev, A., Komissarova, K., Ivanova, A., Sergeeva, M., Safina, K., Nabieva, E., Klink, G., Garushyants, S., Zabutova, J., Kholodnaia, A., Skorokhod, I., Ryabchikova, V.V., Komissarov, A., Lioznov, D. Emergence of Y453F and Δ69–70HV mutations in a lymphoma patient with long-term COVID-19. https://virological.org/t/emergence-of-y453f-and-69-70hv-mutations-in-a-lymphoma-patient-with-long-term-covid-19/580?fbclid=IwAR0fMWUrXHqEhpU0j0LI_-cWuF4G-PbC_qAZWtqkZce943OffhdkLyNoFzw (2021).
Makhoul, M. et al. Epidemiological impact of SARS-CoV-2 vaccination: Mathematical modeling analyses. Vaccines (Basel) 8, 668 https://doi.org/10.3390/vaccines8040668 (2020).
Petrova, V. N. & Russell, C. A. The evolution of seasonal influenza viruses. Nat. Rev. Microbiol. 16, 47–60 (2018).
Liu, W. et al. Two-year prospective study of the humoral immune response of patients with severe acute respiratory syndrome. J. Infect. Dis. 193, 792–795 (2006).
Tang, F. et al. Lack of peripheral memory B cell responses in recovered patients with severe acute respiratory syndrome: A six-year follow-up study. J. Immunol. 186, 7264–7268 (2011).
Cao, Y., Gillespie, D. T. & Petzold, L. R. Avoiding negative populations in explicit Poisson tau-leaping. J. Chem. Phys. 123, 054104 (2005).
Kiyuka, P. K. et al. Human coronavirus NL63 molecular epidemiology and evolutionary patterns in rural coastal Kenya. J. Infect. Dis. 217, 1728–1739 (2018).
Acknowledgements
We thank Alexey Kondrashov, Nick Machnik, Raimundo Julian Saona Urmeneta, Gasper Tkacik and Nick Barton for fruitful discussions. We also thank participants of EvoLunch seminar at IST Austria and the internal seminar at the Banco de España for useful comments. The opinions expressed in this document are exclusively of the authors and, therefore, do not necessarily coincide with those of the Banco de España or the Eurosystem. ETD is supported by the Swiss National Science and Louis Jeantet Foundation. The work of FAK was in part supported by the ERC Consolidator Grant (771209-CharFL).
Author information
Authors and Affiliations
Contributions
E.T.D. and F.A.K. formulated the question. S.A.R. and Y.A.K. formulated the model. S.A.R. programmed and ran the model. All authors jointly analyzed the results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rella, S.A., Kulikova, Y.A., Dermitzakis, E.T. et al. Rates of SARS-CoV-2 transmission and vaccination impact the fate of vaccine-resistant strains. Sci Rep 11, 15729 (2021). https://doi.org/10.1038/s41598-021-95025-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-95025-3
This article is cited by
-
A computational model of epidemic process with three variants on a synthesized human interaction network
Scientific Reports (2024)
-
Policy makers believe money motivates more than it does
Scientific Reports (2024)
-
Seroprevalence of anti-SARS-CoV-2 antibodies and factors associated with infection among adolescent men who have sex with men and transgender women in Salvador, Brazil
BMC Public Health (2023)
-
A mathematical model for COVID-19 considering waning immunity, vaccination and control measures
Scientific Reports (2023)
-
COVID-19 activity risk calculator as a gamified public health intervention tool
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.