Testing average wind speed using sampling plan for Weibull distribution under indeterminacy

Abstract

The time truncated plan for the Weibull distribution under the indeterminacy is presented. The plan parameters of the proposed plan are determined by fixing the indeterminacy parameter. The plan parameters are given for various values of indeterminacy parameters. From the results, it can be concluded that the values of sample size reduce as indeterminacy values increase. The application of the proposed plan is given using wind speed data. From the wind speed example, it is concluded that the proposed plan is helpful to test the average wind speed at smaller values of sample size as compared to existing sampling plan.

Introduction

Wind speed is an important parameter of wind energy. The meteorologists are interested to estimate the average wind speed for the next day, next month, or maybe for the next year, see¹ for more details. In such a case, the meteorologists are interested to test the null hypothesis that the average wind speed is equal to the specified average speed versus the alternative hypothesis that average wind speed differs significantly. At the time of testing the hypothesis, it may not possible to record the average wind speed for a whole year for example. In this case, a random sample of days can be selected and the average wind speed can be recorded for those selected days only. The null hypothesis can be rejected if the daily average wind speed, say acceptance number of days, is more than or equal to the specified average wind speed during the given number of days. For example, let the specified average wind speed is 7mph and the average wind speed of 30 days is recorded. Let the meteorologists are decided to record the average wind speed for 10 days (acceptance number of days). Based on this information, the null hypothesis that the average wind speed is equal to 7 mph will be rejected if in 30 days, if the daily average wind speed in 10 days is less than 7 mph, otherwise, the alternative hypothesis is accepted. As the decision of daily average wind speed is taken on the basis of sample information, therefore, two types of errors are associated with testing the average wind speed. The probability that rejecting the null hypothesis when it is true is called the type-I error and the probability of accepting it when wrong is known as type-II error. The acceptance sampling plan can help meteorologists to choose the sample size of days and acceptance number of days that minimize both errors. The details about the acceptance sampling plans can be seen in^2,3.

The wind speed data is recorded at random and follows the statistical distribution. Among other statistical distributions, the Weibull distribution has been applied widely for estimating and forecasting the wind speed. Akpinar et al.⁴ presented the statistical study for wind speed data. Yilmaz and Çelik⁵ discussed the statistical method to estimate wind speed. Ali et al.⁶ applied the Weibull distribution and Rayleigh distribution for the wind speed data. Arias-Rosales and Osorio-Gómez⁷ used the statistical analysis for estimating energy cost. The comparisons of wind speed distributions can be seen in^8,9,10,11 used the Weibull distribution for modeling wind speed data. Campisi-Pinto et al.¹² presented the statistical tests for surface wind speed. ul Haq et al.¹³ applied the Marshall–Olkin Power Lomax distribution for wind speed estimation. More applications of statistical techniques in analyzing the wind speed data can be read in^14,15,16,17.

For estimating and forecasting, the statistical distributions under classical statistics can only be applied when the observations or the parameters are determined. Usually, the daily wind speed data is recorded in intervals. In this case, the statistical distributions under classical statistics cannot be applied. Alternately, the statistical methods using fuzzy logic can be applied for estimating purposes. Jamkhaneh et al.¹⁸ worked on the single sampling plan using a fuzzy approach. Jamkhaneh et al.¹⁹ discussed the effect of sampling error on inspection using a fuzzy approach. Sadeghpour Gildeh et al.²⁰ proposed a single plan using fuzzy logic. Afshari and Sadeghpour Gildeh²¹ proposed the improved sampling plan using fuzzy logic. For details, the reader may refer to^22,23.

The neutrosophic logic gives information about the measure of determinacy, and indeterminacy and measure of falseness, see²⁴. Therefore, the neutrosophic logic is more efficient than the fuzzy logic and interval-based analysis. Later on, several authors worked on neutrosophic logic for various real problems and showed its efficiency over fuzzy logic, see, for example^{25,26,27,28,29,30}. The idea of neutrosophic statistics was given using the idea of neutrosophic logic^31,32,33. The neutrosophic statistics gives information about the measure of determinacy and measure of indeterminacy, see³⁴. The neutrosophic statistics reduces to classical statistics if no information is recorded about the measure of indeterminacy. References^35,36,37,37 proposed the acceptance sampling plans using the neutrosophic statistics. Aslam et al.³⁸ proposed the time-truncated group plans for the Weibull distribution. Alhasan and Smarandache³⁹ worked on neutrosophic Weibull and neutrosophic family of Weibull distribution.

The existing sampling plans based on classical statistics and fuzzy logic do not give information about the measure of indeterminacy. By exploring the literature and best of our knowledge, there is no work on a time-truncated plan for the neutrosophic Weibull distribution. In this paper, the neutrosophic Weibull distribution is introduced and applied for testing the daily average wind speed. The plan parameters for testing the hypothesis will be determined by minimizing type-I and type-II errors. It is expected that a smaller sample size is needed for testing the average wind speed using the proposed sampling plan.

Methodology

In this section, the Weibull distribution under neutrosophic statistics is introduced. We will also present the design of the sampling scheme plan for testing the average wind speed under an indeterminate environment.

Preliminaries

Suppose that $f\left({x}_{N}\right)=f\left({x}_{L}\right)+f\left({x}_{U}\right){I}_{N};{I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]$ be a neutrosophic probability density function (npdf) having determinate part $f\left({x}_{L}\right)$, indeterminate part $f\left({x}_{U}\right){I}_{N}$ and indeterminacy interval ${I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]$. Note that ${x}_{N}\epsilon \left[{x}_{L},{x}_{U}\right]$ be a neutrosophic random variable follows the npdf. The npdf is the generalization of pdf under classical statistics. The proposed neutrosophic form of $f\left({x}_{N}\right)\epsilon \left[f\left({x}_{L}\right),f\left({x}_{U}\right)\right]$ reduces to pdf under classical statistics when $I_{L} = 0$. Based on this information, the npdf of the Weibull distribution is defined as follows

$$f\left( {x_{N} } \right) = \left\{ {\left( {\frac{\beta }{\alpha }} \right)\left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta - 1} e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} } \right\} + \left\{ {\left( {\frac{\beta }{\alpha }} \right)\left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta - 1} e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} } \right\}I_{N} p;I_{N} \in \left[ {I_{L} ,I_{U} } \right]$$

(1)

where $\alpha$ and $\beta$ are scale and shape parameters, respectively. Note here that the proposed npdf of the Weibull distribution is the generalization of pdf of the Weibull distribution under classical statistics. The neutrosophic form of the npdf of the Weibull distribution reduces to the Weibull distribution when $I_{L} = 0$. The neutrosophic cumulative distribution function (ncdf) of the Weibull distribution is given by

$$F\left( {x_{N} } \right) = 1 - \left\{ {e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} \left( {1 + I_{N} } \right)} \right\} + I_{N} ; I_{N} \in \left[ {I_{L} ,I_{U} } \right]$$

(2)

The neutrosophic mean of the Weibull distribution is given by

$$\mu_{N} = \alpha {\Gamma }\left( {1 + 1/\beta } \right)\left( {1 + I_{N} } \right);I_{N} \in \left[ {I_{L} ,I_{U} } \right]$$

(3)

The median life for the neutrosophic Weibull distribution is given by

$$\tilde{\mu }_{N} = \alpha \left( {{\text{ln}}\left( 2 \right)} \right)^{1/\beta } \left( {1 + I_{N} } \right);I_{N} \in \left[ {I_{L} ,I_{U} } \right]$$

(4)

Methodology

The null and alternative hypotheses for the average wind speed are stated as follows:

$$H_{0} :\mu = \mu_{0} \;{\text{Vs}}{.}\;H_{1} :\mu \ne \mu_{0}$$

where $\mu$ is true average wind speed and ${\mu }_{0}$ is the specified average wind speed. Based on this information, the proposed sampling plan is stated as follows

Step 1 Select a random sample of $n$ number of days and record the daily average speed for these selected days. Specify the number of days, say $c$, average wind speed ${\mu }_{0}$ and indeterminacy parameter ${I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]$.

Step 2 Accept ${H}_{0}:\mu ={\mu }_{0}$ if daily average wind speed in $c$ days is more than or equal to ${\mu }_{0}$, otherwise, reject ${H}_{0}:\mu ={\mu }_{0}$.

The proposed sampling scheme is characterized by the three parameters $n$, $c$ and ${I}_{N}$, where ${I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]$ is considered as the specified parameter and set according to the uncertainty level. Suppose that ${t}_{0}=a{\mu }_{0}$ be the time in days, where $a$ is the termination ratio. The probability of accepting ${H}_{0}:\mu ={\mu }_{0}$ is given by

$$L\left( p \right) = \mathop \sum \limits_{i = 0}^{c} \left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)p^{i} \left( {1 - p} \right)^{n - i}$$

(5)

where $p$ is the probability of rejecting ${H}_{0}:\mu ={\mu }_{0}$ and obtained using Eqs. (2) and (3) and defined by

$$p=1-\left\{\mathrm{exp}(-{a}^{\beta }{\left(\mu /{\mu }_{0}\right)}^{-\beta }{{\left(\Gamma \left(1/\beta \right)/\beta \right)}^{\beta }\left(1+{I}_{N}\right)}^{\beta })\left(1+{I}_{N}\right)\right\}+{I}_{N}$$

(6)

where $\mu /{\mu }_{0}$ is the ratio of true average daily wind speed to specified average daily wind speed. Suppose that $\stackrel{\sim }{\alpha }$ and $\stackrel{\sim }{\beta }$ be type-I and type-II errors. The meteorologists are interested to apply the proposed plan for testing ${H}_{0}:\mu ={\mu }_{0}$ such that the probability of accepting ${H}_{0}:\mu ={\mu }_{0}$ when it is true should be larger than $1-\stackrel{\sim }{\alpha }$ at $\mu /{\mu }_{0}$ and the probability of accepting ${H}_{0}:\mu ={\mu }_{0}$ when it is wrong should be smaller than $\stackrel{\sim }{\beta }$ at $\mu /{\mu }_{0}=1$. The plan parameters for testing ${H}_{0}:\mu ={\mu }_{0}$ will be obtained such that the following two inequalities are satisfied.

$$L\left({p}_{1}|\mu /{\mu }_{0}=1\right)\le \stackrel{\sim }{\beta }$$

(7)

$$L\left({p}_{2}|\mu /{\mu }_{0}\right)\ge 1-\stackrel{\sim }{\alpha }$$

(8)

where ${p}_{1}$ and ${p}_{2}$ are defined by

$${p}_{1}=1-\left\{\mathrm{exp}(-{a}^{\beta }{{\left(\Gamma \left(1/\beta \right)/\beta \right)}^{\beta }\left(1+{I}_{N}\right)}^{\beta })\left(1+{I}_{N}\right)\right\}+{I}_{N}$$

(9)

and

$${p}_{2}=1-\left\{\mathrm{exp}(-{a}^{\beta }{\left(\mu /{\mu }_{0}\right)}^{-\beta }{{\left(\Gamma \left(1/\beta \right)/\beta \right)}^{\beta }\left(1+{I}_{N}\right)}^{\beta })\left(1+{I}_{N}\right)\right\}+{I}_{N}$$

(10)

The values of the plan parameters $n$ and $c$ for various values of $\stackrel{\sim }{\beta }$, $\stackrel{\sim }{\alpha }=0.10$, $a$ and ${I}_{N}$ are placed in Tables 1, 2, 3, 4, 5 and 6. Tables 1 and 2 are shown for the exponential distribution case. For exponential distribution, it can be seen that the values of $n$ decreases as the values of $a$ increases from 0.5 to 1.0. On the other hand for other the same parameters, the values of $n$ decreases as the values of $\beta$ increases. Note here that the indeterminacy parameter ${I}_{N}$ also plays a significant role in minimizing the sample size.

Table 1 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =1$ and $a=0.50$.

Table 2 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =1$ and $a=1.0$.

Table 3 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =2$ and $a=0.50$.

Table 4 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =2$ and $a=0.10$.

Table 5 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =3$ and $a=0.50$.

Table 6 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =3$ and $a=0.10$.

Comparative study

In this section, the efficiency of the proposed plan is discussed in terms of sample size. The smaller the sample size means that less cost is needed for testing the hypothesis about the daily average wind speed. Note here that the proposed sampling plan is the generalization of the plan under classical statistics when no uncertainty/indeterminacy is found in recording the daily average wind speed. The proposed sampling plan reduces to the existing sampling plan when ${I}_{N}$=0. The first column in Tables 1, 2, 3, 4, 5 and 6 presents the plan parameters under the classical statistics. From Tables 1, 2, 3, 4, 5 and 6, it can be noted that the values of the sample size required for testing ${H}_{0}:\mu ={\mu }_{0}$ decreasing as the indeterminacy parameter ${I}_{N}$ increases. For example, when $\mu /\mu_{0} = 1.1$ and $a = 0.5$ from Table 1, it can be seen that $n = 1143$ from the plan under classical statistics and $n = 1010$ for the proposed sampling plan when $I_{N} = 0.05$. From the study, it is concluded that the proposed plan under indeterminacy is efficient in sample size as compared to the existing sampling plan under classical statistics. Therefore, the application of the proposed plan for testing the null hypothesis ${H}_{0}:\mu ={\mu }_{0}$ requires a smaller sample as compared to the existing plan. The meteorologist can apply the proposed plan under uncertainty with fewer effort and time.

Application for wind speed data

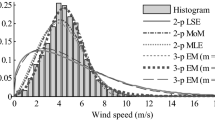
The application of the proposed sampling plan will be discussed using wind speed data. The wind speed is a big and important source of energy. Due to the randomness and uncertainty, the wind speed data follows the statistical distribution under neutrosophic statistics. The meteorologists are interested to see the daily average wind speed under indeterminacy. The average wind speed data of Cairo city is taken from⁴⁰ and shown in Table 7. It is found that the wind speed data follows the Weibull distribution with shape parameter $\widehat{\beta }=$ 2.7857 and scale parameter $\alpha =8.05$. The plan parameters for this shape parameter are shown in Tables 8 and 9. For the proposed plan, the shape parameter is ${\widehat{\beta }}_{N}=(1+0.02)\times 2.7857 \approx 3$ when $I_{U} = 0.02$. Suppose that meteorologists are interested to test $H_{0} :\mu = 7.15$ with the aid of the proposed sampling plan when $I_{U} = 0.02$, $\tilde{\alpha } = 0.10$, $\mu /\mu_{0} = 1.3$, $a = 0.5$ and $\tilde{\beta } = 0.25$. From Table 5, it can be noted that $n = 100$ and $c = 7$. The proposed sampling plan will be implemented as: accept the null hypothesis ${H}_{0}:\mu =7.15$ if average daily speed in 7 days is more than equal to 7.15mph. From the data, it can be noted average daily wind speed is more than equal to 7.15mph in more than 7 days, therefore, the claim about the average daily wind speed ${H}_{0}:\mu =7.15$ will be accepted. From the real example, it is concluded that the proposed sampling will be helpful to check the daily average wind speed.

Table 7 The daily average wind speed data.

Table 8 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =2.7857$ and $a=0.50$.

Table 9 The plan parameter when $\stackrel{\sim }{\alpha }=0.10;\beta =2.7857$ and $a=0.10$.

Concluding remarks

The time truncated plan for the Weibull distribution under the indeterminacy was presented. The plan parameters of the proposed plan were determined by fixing the indeterminacy parameter. The plan parameters were given for various values of indeterminacy parameters, shape parameter, and scale parameter. Several tables for the application of the proposed plan are given. The application of the proposed plan was given with the help of daily average wind speed. The testing of the hypothesis was done to test the average daily wind speed. From the study, it is concluded that the indeterminacy parameter plays a significant role in fixing the plan parameters. The less sample size is needed as the indeterminacy parameter increased. In addition, it is found that the proposed plan is efficient than the existing sampling plan in terms of sample size. To save time, efforts, and energy, it is recommended to apply the proposed plan for testing the average wind speed. The proposed plan can be applied in metrology, oceanography, and thermodynamics. The proposed plan can be applied for testing big data from oceanography as future research. By following^41,42, the software for goodness of fit tests using the npdf in Eq. (1) can be developed as future research.