Introduction

Ti3AlC2 belongs to the family of Mn+1AXn (MAX) phases with more than 80 members. These are layered, machinable, nanolaminated ternary carbides, nitrides and borides, where M is an early transition metal, A is an A-group element, mainly from groups 13–16 and X is C or N or B1,2,3. These compounds possess hexagonal crystal structure with space group P63/mmc (space group number: 194), where M atoms are in a near closed packed arrangement and are intercalated with A-group atomic layers, with the X-atoms residing in the octahedral sites between the M layers. These atomic arrangements give the MAX phases an effective laminated layered structure that leads to the naming of the MAX phase as nanolaminates4. MAX phases possess a unique combination of properties, both metallic and ceramic in nature due to the layered structure. Metallic properties can include good thermal and electrical conductivities, good thermal shock resistance, excellent damage tolerance, and good machinability. Ceramic properties include low density, elastic rigidity, oxidation and creep resistance, and the ability to maintain the strength up to very high temperatures3,4,5.

These properties constitute MAX phases technologically important materials. There are potential uses of MAX phases as high temperature heating elements, tough, machinable and thermal shock resistant refractories, neutron irradiation resistant parts for nuclear applications, coatings for electrical contacts, precursor for the synthesis of carbide-derived carbon and MXenes, a family of two-dimensional transition metal carbides, nitrides, borides, and carbonitrides3,4,5,6.

The structures as well as the properties of MAX phases can be altered, and even improved, by hosting a new element into the lattice. The inclusion of a new element on the M, A, and/or X sites leads to isostructural MAX phase solid solutions. In recent time, a growing interest in MAX phase solid solutions is seen in the scientific community as a way to obtain improved properties. For example the phase Ti3SiC2 is found to be more oxidation resistant when Al on A-site or Nb on M-site is introduced to form Ti3(Si1−xAlx)C2 or (Nb1−xTix)3SiC2 solid solutions7,8. Meng et al.9 and Barsoum et al.10 reported on the solid solution hardening effect for (VxTi1−x)2AlC and Ti2AlCxNy, respectively. A solid solution softening effect was reported by Bei et al.11 for Ti3(Al1−xSnx)C2. The partial inclusion of Ti on the M-site in Nb4AlC3 improves the mechanical properties12, flexural strength, fracture toughness and Vickers hardness13 significantly. Structural, magnetic, and electrical and thermal transport properties are observed to modify as the x-content in Cr2−xMxGeC (M = Ti, V, Mn, Fe, and Mo) increases14. M-site solid solutions with partial inclusion of Zr, Hf, and Nb enhance the elastic moduli and strength of Ti3SiC2 at elevated temperatures15. Incorporation of Si in Ti3AlC2 can improve Young’s and shear moduli significantly16. According to a theoretical study, the partial inclusion of Nb atoms in Ti2SC and Zr2SC improves the mechanical strength17.

M-site solid solutions (Zr3−xTix)AlC2 have been reported recently and a density functional theory (DFT) calculation described their mechanical and thermodynamic properties18,19. Synthesis of Zr3(Al1−xSix)C2 has been associated with an improvement of the free energy barrier for nucleation, without preferential, competitive phase formation20. Successful synthesis of (Zr,M)2AlC and Zr2(Al,A)C compounds with variable compositions has been reported21,22. Furthermore, alloying effects on the M-site in M2AlC (M = Ti, V, Zr, and Hf) with elements in the first transition metal row as well as Ca and Sc have been investigated theoretically23. Meanwhile, phase stability and physical properties of (Zr1−xNbx)2AlC MAX phases have also been predicted recently24.

A renewed interest on MAX phases has grown in the scientific community after the synthesis of phase pure, dense bulk Ti3SiC2 in 199625. This phase has become among the most studied MAX phases due to the combination of strength, machinability and ductility at high temperatures, in addition to non-susceptibility to thermal shock, never observed previously in any other MAX phase material26. On the other hand, Ti3AlC2 is the only ceramic that exhibits room temperature compressive plasticity27,28. Moreover, Ti3AlC2 exhibits excellent oxidation resistance at high temperature due to formation of a pure alumina protective oxide layer29. For this reason, it is expected that the MAX phase solid solutions Ti3(Al1−xSix)C2 may be enriched with a good set of properties to make them technologically important materials. It is thus not surprising that these solid solutions have been investigated extensively both experimentally and theoretically7,30,31,32,33,34,35,36,37,38. All previous theoretical and experimental studies on Ti3(Al1−xSix)C2 have been accomplished with x = 0, 0.25, 0.33, 0.37, 0.50, 0.625, 0.67, 0.75, 0.875, and 1.0. The samples prepared in previous experimental studies were not highly pure. So, the physical properties described in those studies were not able to address properly the Ti3(Al1−xSix)C2 solid solutions. In the same manner, the theoretical results cannot be justified accurately.

Recently, a series of new high-purity Ti3(Al1−xSix)C2 solid solutions with varying compositions (x = 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0) have been reported and their lattice parameters, elastic modulus, heat capacities and thermal expansion coefficient have been experimentally investigated to examine the effects of the amount of Si in Ti3(Al1−xSix)C2 solid solutions on their structural, physical and mechanical properties16. The present DFT study aims to investigate the physical properties of Ti3(Al1-−Six)C2 solid solutions from a theoretical perspective and to validate the DFT based first-principles methods using the more recently available experimental results.

Results and discussions

Structural properties

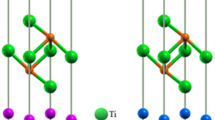
The supercell of Ti3(Al1−xSix)C2 with x = 0.2 is shown in Fig. 1a. The optimized lattice parameters are listed in Supplementary Table 1 along with the experimental values. Figure 1b also shows these results as a function of Si content x, where the near linear trend indicates a good agreement with Vegard’s law for solid solutions39. With the increase of silicon content x, a decrease of cell parameters (negligible in a and significant in c as well as in V) is observed. The Al-containing Ti3AlC2 has a unit cell larger than that of the Si-containing Ti3SiC2 as the Al has larger covalent atomic radius (1.18 Å) compared to that of Si (1.11 Å). The deviation of lattice parameters calculated in this study from the corresponding experimental values is within 0.2% for a, 1.1% for c and 1.2% for V, indicating the reliability of the present investigations. The GGA trend in lattice parameters is also observed in this study.

Figure 1
figure 1

Structural properties for the considered MAX solid solutions. (a) Supercell of Ti3(Al1−xSix)C2 with x = 0.2. (b) Structural properties of Ti3(Al1−xSix)C2 as a function of Si-content x. Solid and open symbols represent the calculated and experimental16 values, respectively.

Full size image
Table 1 Single crystal elastic constants Cij, elastic moduli (B, G, E) and Cauchy pressure Pc = C12–C44 (in GPa), Pugh’s ratio B/G and Poisson’s ratio v of Ti3(Al1−xSix)C2.
Full size table

Electronic and bonding properties

The ground state electronic band structures of Ti3(Al1−xSix)C2 calculated along high symmetry directions in the first Brillouin zone are shown in Supplementary Fig. 1. The band structures show dense regions of valence and conduction bands connected by highly dispersive bands within a window of about 2 eV around the Fermi level, indicating metallic bonding nature of all compositions of Ti3(Al1−xSix)C2. The overlap of the dispersive bands and the dense conduction band region occurs at the Γ-point at about 1 eV above the Fermi level. This intersection (or overlap) point shows the tendency to be closer to the Fermi level as Si-content x increases from 0 to 1. The energy dispersions along different directions are different, indicating the lattice anisotropy in Ti3(Al1−xSix)C2. The lowest valence bands occupy the energy states between –12 and –9.6 eV. A band gap above the lowest valence bands appears for x = 0. This gap reduces gradually as x increases and fully disappears for x = 0.6 and an intermediate valence band appears between the upper and lower valence bands (see DOS profiles). The increase of Si-content x significantly reduces the d-resonance around the Fermi level of the transition metal Ti. This can be seen more clearly in Supplementary Fig. 2, wherein the electronic density of states (DOS) is depicted.

Figure 2
figure 2

Variation of the investigated mechanical properties as a function of Si-content x in Ti3(Al1−xSix)C2 solid. (a) Elastic constants. (b) Elastic moduli. (c) Cauchy pressure. (d) Pugh’s and Poisson’s ratio.

Full size image

In order to understand the nature of chemical bonding in Ti3(Al1−xSix)C2, the total density of states (TDOS) as well as the partial density of states (PDOS) are calculated and shown in Supplementary Fig. 2. The Fermi level is denoted with a vertical broken line, which is set at 0 eV in the energy scale defined by E − EF. For x = 0, i.e., for Ti3AlC2, the TDOS in the Fermi level is placed at a dip, which is known as a pseudogap, signifying the structural stability of this phase. The Fermi level gradually moves away from the pseudogap towards the upper bound (right direction) when the value of the Si content x goes from zero to unity. This means that the structural stability reduces gradually when the amount of Si increases within the Ti3(Al1−xSix)C2 system. The finite value N(EF) of TDOS at the Fermi level for all x values resulting from d-resonance of the transition metal Ti indicates metallic bonding of Ti3(Al1−xSix)C2. N(EF) decreases gradually up to x = 0.6 and then increases but the value of N(EF) for x = 1.0 does not exceed the value for x = 0.0.

The lowest valence band situated between –12 and –9.2 eV arises due to hybridization of C 2s with Ti 3d electrons in the two end members of Ti3(Al1−xSix)C2. In other cases, together with C 2s orbital, almost equal contribution comes from Si 3s electrons. All of these interactions indicate covalent Ti-C and Ti-Si bonding. The higher valence band consists of several distinct peaks. The left peak of the middle region (–4 to –1 eV) arises as a result of interaction between C 2p and Ti 3d electrons for two end members of Ti3(Al1−xSix)C2. For x = 0.2 and 0.4, mainly Si 3p and C 2p lead to form such peaks, while for x = 0.6 and 0.8, Al 2p instead of Si 3p contributes similarly. For the two end members, the middle maximum is due to C 2p and Ti 3d electrons. For x = 0.2 and 0.4, an additional large contribution comes from Si 3p electrons, while for x = 0.6 and 0.8, this contribution comes from Al 2p electrons. The right peak of the middle region is close to the Fermi level, which corresponds to the hybridization between Ti 3d and Al 2p/Si 3p electrons in two end members, respectively. This hybridization leads to weaker Ti–Al and Ti-Si covalent bonding in Ti3AlC2 and Ti3SiC2, respectively. The bond length between Ti and Al (2.908 Å) is larger than that of between Ti and Si (2.701 Å) when Al is entirely substituted by Si. On the other hand, the bond population of Ti–Al bond (0.60) is smaller than that of Ti-Si bond (0.76) when Al is completely replaced by Si. Therefore, the Ti-Si bond is stronger than the Ti–Al bond. The relative strengths and lengths of these particular bonds are responsible for the increase of elastic constants and moduli and hence the mechanical strength of Ti3(Al1−xSix)C2 with the increase of x (refer to Table 1). For x = 0.2–0.8, the right peak indicates the presence of both Ti–Al and Ti-Si covalent bonding. The conduction band for all x arises mainly from the Ti 3d electrons. For pure solid solutions (x = 0.2–0.8), the contributions in chemical bonding are different from those of the two end members. It is expected that this difference will lead to significant modification of the physical properties of the two end members. The chemical bonding in the solid solutions Ti3(Al1−xSix)C2 is obviously a mixture of metallic, covalent and, due to the difference in electronegativity between the comprising elements, ionic in nature.

Mechanical properties

Knowledge of elastic constants is of high importance to analyze the mechanical behaviors of crystalline solids. MAX phases have five independent elastic constants Cij, namely, C11, C33, C44, C12, and C13 due to their hexagonal crystal symmetry. The calculated elastic constants of Ti3(Al1−xSix)C2 for Si-content x = 0.0, 0.2, 0.4, 0.6, 0.8, and 1.0 are listed in Table 1 and shown in Fig. 2a. All compositions are mechanically stable as they satisfy the Born criteria40. A monotonous increase in elastic constants is observed with the increase of Si-content x. It means that the mechanical strength and stiffness increase with Si content x. C33 increases at a faster rate and C12 at a slower rate than other Cij. This means that the elastic stiffness along the c-axis increases with Si content x at a faster rate than that along the a- and b-axes.

Bulk and shear moduli (B and G) are calculated using the Voigt–Reuss–Hill (VRH) approximation41. These parameters are listed in Table 1 and shown in Fig. 2b. Both moduli increase with Si content x. The calculated shear modulus G is consistent with the measured values16 in the whole compositional range. The larger the shear modulus, the more rigid the material behaves. This leads to evaluate the sensitivity of the material to strain variation. The shear modulus assesses the elastic behavior of a material due to shear loading. With Si content x, the rigidity of Ti3(Al1−xSix)C2 increases almost linearly.

The Young’s modulus E is calculated from B and G by using: E = 9BG/(3B + G). This modulus is somewhat larger than the measured values at room temperature16. The reason is that the higher the temperatures the lower the Young’s modulus. After that their increasing trends with Si content x are almost similar. This modulus measures the resistance of a material to elastic deformation under a load. A stiff material has a high Young's modulus and changes its shape only slightly under elastic loads. The Si content x increases the stiffness of Ti3(Al1−xSix)C2. The Young’s modulus is also related to the thermal shock resistance R5. The lower the Young’s modulus, the higher the thermal shock resistance. Therefore, Ti3AlC2 has better thermal shock resistance among all compositions of Ti3(Al1−xSix)C2.

The Cauchy pressure defined as Pc = C12 − C44 is shown in Fig. 2c. It can evaluate the failure modes of solids and the nature of chemical bonding5. A negative (positive) value of Pc is always associated with the brittle (ductile) failure of solids. Accordingly, the solid solution Ti3(Al1−xSix)C2 is brittle in nature and its brittleness increases monotonically with the Si content x. A negative Cauchy pressure corresponds to directional covalent bonding with angular character, while a positive Cauchy pressure signifies metallic bonding. Therefore, all compositions of Ti3(Al1−xSix)C2 are dominated by directional covalent bonding and its covalency increases with the increase of Si content x.

The Pugh’s ratio B/G serves as a decisive factor for classifying solid materials into brittle and ductile groups. A value of 1.75 for B/G plays this role and is known as the border line for separating the brittle materials from ductile ones5 (see Fig. 2d). Values lower (higher) than this value is associated with a brittle (ductile) material. It is evident that all compositions of Ti3(Al1−xSix)C2 are brittle in nature as is predicted from the Cauchy pressure.

The Poisson’s ratio v is used to predict many physical properties of materials. The stability of a compound against shear can be predicted by a low Poisson’s ratio6. Thus all compositions of Ti3(Al1−xSix)C2 are stable against shear. The interatomic forces in crystalline solids can be predicted as central forces if their Poisson’s ratios range from 0.25 to 0.50, otherwise they will be non-central forces6. Clearly, all compositions of Ti3(Al1−xSix)C2 are stabilized with non-central forces. The non-central force is the characteristic of brittle materials. The nature of chemical bonding is found to be purely covalent or totally metallic for a crystal whose Poisson’s ratio is 0.1 or 0.336. All compositions of Ti3(Al1−xSix)C2 possess the values between these two characteristic values and exhibit partially metallic and covalent nature. Brittle materials are characterized by a Poisson’s ratio lower than a typical value of 0.26 and ductile materials possess a value larger than 0.266. In this scale, all compositions of Ti3(Al1−xSix)C2 should exhibit brittleness as predicted from the Cauchy pressure and Pugh’s ratio (see Fig. 2d).

Thermal properties

Debye temperature and melting point

The Debye temperature, a characteristic temperature, can be used to assess many physical properties of solids, including thermal expansion, thermal conductivity, lattice vibrations, melting temperature, and specific heat. It is also linked to the superconducting transition temperature and the electron–phonon coupling constant in the case of superconductors. Moreover, the vacancy formation energy in metals can depend upon the Debye temperature. For calculating this characteristic temperature, the Anderson method is simple and rigorous among several methods. According to this method the Debye temperature θD can be expressed using the average sound velocity vm via the expression42:

$$\theta_{{\text{D}}} = \frac{h}{{k_{{\text{B}}} }}\left[ {\left( {\frac{3n}{{4\pi }}} \right)\frac{{N_{{\text{A}}} \rho }}{M}} \right]^{1/3} v_{{\text{m}}} .$$
(1)

Here, h and kB are respectively the Planck and Boltzmann constants, NA is the Avogadro’s number, ρ is the density of mass, n is the number of atoms in a molecule, and M is the molecular weight. The average sound velocity vm is calculated from the longitudinal and transverse sound velocities vl and vt by the equation:

$$v_{{\text{m}}} = \left[ {\frac{1}{3}\left( {\frac{1}{{v_{{\text{l}}}^{3} }} + \frac{2}{{v_{{\text{t}}}^{3} }}} \right)} \right]^{ - 1/3} .$$
(2)

Using the bulk and shear moduli, vl and vt can be calculated as

$$v_{{\text{l}}} = \left( {\frac{3B + 4G}{{3\rho }}} \right)^{1/2} \;{\text{and}}\;v_{{\text{t}}} = \left( {\frac{G}{\rho }} \right)^{1/2} .$$
(3)

The Debye temperature and sound velocities calculated for Ti3(Al1−xSix)C2 MAX phases are listed in Table 2 and plotted in Fig. 3a, indicating that the Debye temperature increases with the increase of Si content x. High mass density of Si leads to high Debye temperature of Ti3(Al1−xSix)C2 with the increase of Si content x. Commonly, the lower the Debye temperature, the softer the material. Therefore, Ti3AlC2 is softer than Ti3SiC2. A comparatively low Debye temperature should lead to low thermal conductivity of Ti3AlC, which favors it to be a promising TBC material43.

Table 2 Density (ρ; g/cm3), sound velocities (vl, vt, vm; km/s), Debye and melting temperatures (θD, Tm; K), and minimum and lattice thermal conductivities (kmin, kph; W/m K).
Full size table
Figure 3
figure 3

Variation of the investigated thermal properties as a function of Si-content x in Ti3(Al1−xSix)C2 solid solutions. (a) Debye and melting temperatures. (b) Minimum and room temperature lattice thermal conductivity. (c) Temperature dependence of lattice thermal conductivity.

Full size image

An empirical formula: Tm = 354 + 1.5(2C11 + C33) developed for hexagonal crystals is used to calculate the melting point of Ti3(Al1−xSix)C2 MAX phases44. The calculated Tm is shown in Table 2 and Fig. 3a. It is evident that the melting temperature increases with the increase of Si-content x. Higher melting temperature implies that the solid solutions Ti3(Al1−xSix)C2 should have potential applications in harsh environments.

Lattice thermal conductivity

For applications at high temperatures the materials are selected on the basis of their lattice thermal conductivity as well as on their minimum thermal conductivity. The DFT calculation of the lattice thermal conductivity for MAX phases is not simple owing to their dual properties between metals and ceramics. Therefore, a perfect method based on a modest technique with judicious approximations is greatly anticipated. Slack developed an equation to calculate the lattice thermal conductivity taking into consideration the average of the atoms in a “molecule” (or the atoms in the formula unit of the crystal) and their average atomic weight45. Slack’s model is convenient to determine the temperature-dependent lattice thermal conductivity of MAX phases owing to their partially ceramic nature46, while Clarke’s model is very expedient to calculate the temperature-independent minimum thermal conductivity of compounds. The empirical formula derived by Slack for calculating the lattice thermal conductivity is

$$k_{{{\text{ph}}}} = A\frac{{M_{{{\text{av}}}} \theta_{D}^{3} \delta }}{{\gamma^{2} n^{2/3} T}}.$$
(4)

In this equation, Mav denotes the average atomic mass of a crystal in kg/mol, θD refers to the Debye temperature in K, δ defines the cubic root of average atomic volume in m, n is the number of atoms in the conventional unit cell, T is the temperature in K, and γ is the unitless Grüneisen parameter, which is derived from the Poisson’s ratio using the expression:

$$\gamma = \frac{{3\left( {1 + \nu } \right)}}{{2\left( {2 - 3\nu } \right)}}.$$
(5)

The factor A(γ) due to Julian47 is calculated as

$$A\left( \gamma \right) = \frac{{5.720 \times 10^{7} \times 0.849}}{{2 \times \left( {1 - 0.514/\gamma + 0.228/\gamma^{2} } \right)}}.$$
(6)

The lattice thermal conductivity calculated at room temperature (300 K) for Ti3(Al1−xSix)C2 solid solutions is listed in Table 2 and their room temperature values and temperature dependencies are shown in Fig. 3b,c, respectively. The reliability of the Slack model has been established as evident from the calculated lattice thermal conductivity of Ta4AlC3 (5 W/m–K) being comparable with the experimental value of 6 W/m–K at 1300 K. Moreover, the calculated value for Nb4AlC3 is identical to the experimental value of 7 W/m–K at 1300 K48. With Si-content x the lattice thermal conductivity of Ti3(Al1−xSix)C2 decreases gradually.

The total thermal conductivity at room temperature for MAX phases ranges from 12 to 60 W/m–K in which the electronic contribution to the total thermal conductivity is trivial49. Therefore, it is anticipated that the present values for Ti3(Al1−xSix)C2 solid solutions may not exceed this range if their electronic contribution is considered. The lattice thermal conductivity of Ti3(Al1−xSix)C2 solid solutions at room temperature ranges from 52.7 to 55.3 W/m–K. From Fig. 3c, it is evident that the lattice thermal conductivity decreases gradually with increasing temperature. The compositions with x = 0.0 and x = 0.4, respectively have the lowest and highest lattice thermal conductivity in the whole temperature range. The lattice thermal conductivity of Ti3(Al1−xSix)C2 solid solutions follows the order with x: 0.4 > 1.0 > 0.6 > 0.8 > 0.2 > 0.0.

Minimum thermal conductivity

At high temperatures, the inherent thermal conductivity reaches a lower limit, which is known as the minimum thermal conductivity of the compound. At the high temperature, the phonons become completely unpaired and the heat energy transfers to neighboring atoms. In this situation, the mean free path of the phonons is supposed to be the average interatomic distance. Thus, different atoms in a molecule can be replaced with an equivalent atom that has an average atomic mass of M/n (n is the number of atoms in the unit cell) in this approximation. In the cell, a single “equivalent atom” never has the optical modes and can be applied to derive a formula for the minimum thermal conductivity κmin at high temperature as assumed in Clarke’s model50:

$$\kappa_{\min } = { }k_{{\text{B}}} v_{{\text{m}}} \left( {\frac{{nN_{{\text{A}}} \rho }}{M}} \right)^{2/3} .$$
(7)

The symbols in this equation bear the same meanings as in Eq. (4). The minimum thermal conductivity calculated for Ti3(Al1−xSix)C2 solid solutions is shown in Table 2 and Fig. 3b. The minimum thermal conductivity increases with the increase of Si-content x. The minimum thermal conductivity shows linear increasing trend with the Si content x. The end member Ti3AlC2 has a minimum thermal conductivity smaller than that of other compositions including the other end member Ti3SiC2 too.

Optical properties

The optical properties of Ti3(Al1−xSix)C2 MAX phase solid solutions are calculated for the two polarization directions 〈100〉 and 〈001〉 of incident photons. Due to the hexagonal symmetry of MAX phases the incident photon polarization directions 〈100〉 and 〈001〉 correspond to the directions of associated electric field perpendicular and parallel to the crystallographic c-axis, respectively. MAX phases are partially metallic compounds and consequently the intraband transitions have momentous impact at far infrared regions i.e., low energy part of the spectrum. To take account of intraband transition, a phenomenological damping of 0.05 eV, Drude parameters, i.e., the free-electron plasma frequency of 3 eV and Gaussian smearing of 0.5 eV are used for all calculations. The imaginary part of the dielectric function that leads to calculate the remaining optical properties of materials can be expressed as:

$$\varepsilon_{2} \left( \omega \right) = \frac{{2\pi e^{2} }}{{{\Omega }\varepsilon_{0} }}\mathop \sum \limits_{k,v,c} \left| {\psi_{k}^{c} } \right|{\varvec{u}}.{\varvec{r}}\left| {\psi_{k}^{v} } \right|^{2} \delta \left( {E_{k}^{c} - E_{k}^{v} - E} \right)$$
(8)

Here, ω is the frequency of the phonon, e is the electronic charge, Ω is the unit cell volume, u is the unit vector along the polarization of the incident electric field and \(\psi_{k}^{c}\) and \(\psi_{k}^{v}\) are wave functions for conduction and valence band electrons at a particular k, respectively. The expressions for the remaining functions can be found in the literature51.

The real part of the dielectric function ε1(ω) calculated for photon energy of 30 eV is shown in Fig. 4a. Comparing the spectra for 〈100〉 and 〈001〉 polarization directions from left and right panels of Fig. 4a, it can be said that the solid solutions exhibit highly anisotropic nature at the low energy region from 0 to ~ 6 eV. It is seen that the real part ε1(ω) goes through zero in the low energy range, indicating the metallic nature for all compositions of Ti3(Al1−xSix)C2. The static dielectric constant is higher for composition x = 0.2 and lowest for x = 1 when photon is polarized along the 〈100〉 direction. For polarization direction 〈001〉, the static dielectric function is highest for x = 0.4 and lowest for x = 1. All spectra approach zero at 15.5 eV for polarization direction 〈100〉 and at 16 eV for polarization direction 〈001〉. The dielectric function shows highest anisotropic nature for x = 0.4 and lowest for x = 1.

Figure 4
figure 4

Variation of dielectric function as a function of incident photon energy ranged from 0 to 30 eV along the polarization directions 〈100〉 and 〈001〉 for the considered solid solutions Ti3(Al1−xSix)C2. (a) Real part of dielectric function ε1(ω). (b) Imaginary part of dielectric function ε2(ω).

Full size image

Regarding optical phenomena, the imaginary part of the dielectric function ε2(ω) reveals the energy attenuation features of an optical medium with the change of frequency. Figure 4b shows the spectra of ε2(ω) calculated for Ti3(Al1−xSix)C2 MAX solid solutions. For both polarization directions it approaches zero from above, indicating the metallic nature of all compositions. At the IR and visible light regions, the spectral features are different for the two polarization directions, highlighting the anisotropic nature in optical properties. At the high energy region the spectra for both polarizations are almost identical for all compositions. The electronic structure of a material is mostly accountable for optical spectra. For this reason, the origin of the peaks in the spectra can be explained from the DOS plot of the relevant material. To elucidate this link, the composition x = 0 is selected arbitrarily. In the spectrum for polarization 〈001〉, the peak nearby 0.4 eV is due to transitions within Ti 3d orbitals.

The reflectivity of Ti3(Al1−xSix)C2 MAX phases is calculated for the 〈100〉 and 〈001〉 polarization directions and is shown in Fig. 5a. The spectra for both polarizations exhibit distinct features for all compositions with peak’s shapes, heights and positions, indicating anisotropic nature. In the visible region (1.8–3.1 eV), the minimum reflectivity of all compositions for both polarizations is above 45%, which makes them potential candidate materials for coatings to reduce solar heating52. With reflectivity above 51%, the composition with x = 0.2 is a better coating material for preventing solar heating than the other compositions. In the UV region, all compositions exhibit maximum reflectivity between 7.3 and 10.8 eV for the polarization direction 〈100〉. The reflectivity spectra start to decrease drastically at around 21 eV and reach zero value at around 30 eV for both polarizations.

Figure 5
figure 5

Variation of optical properties as a function of incident photon energy ranged from 0 to 30 eV along the polarization directions 〈100〉 and 〈001〉 for the considered solid solutions Ti3(Al1–xSix)C2. (a) Reflectivity R(ω). (b) Optical conductivity σ(ω).

Full size image

The optical conductivity σ(ω) is a key parameter for understanding the electromagnetic response of a material. In the presence of an alternating electric field, it implies electrical conductivity of the material. The photoconductivity can be estimated by means of optical conductivity51. The optical conductivity of Ti3(Al1−xSix)C2 is calculated for the 〈100〉 and 〈001〉 polarization directions, and its real parts are shown in Fig. 5b. The spectra of σ(ω) for both polarization directions show significant diversity in a wide range of photon energy of 0 to 25 eV for all compositions, indicating the anisotropic nature of the optical properties. In the higher-energy region from 25 to 30 eV, the features of the optical conductivity are almost identical for both polarization directions. The peaks in the spectra arise mainly from interband transitions from occupied Ti p orbitals to unoccupied Ti d orbitals.

We further calculate other optical properties such as refractive index, extinction coefficient, absorption coefficient and energy loss function and the results are presented in Supplementary Information section (see Supplementary Figs. 3 & 4).

Conclusion

In summary, we have employed DFT for Ti3(Al1−xSix)C2 solid solutions to calculate the physical properties including structural, electronic, mechanical, thermal and optical properties for the first time. The lattice parameters and elastic moduli calculated in this study show reasonable agreement with experimental results. With the increase of Si content x, a decrease of cell parameters (negligible in a and significant in c as well as in V) occurs. All elastic constants and moduli of Ti3(Al1−xSix)C2 are found to be increased by the Si content x. The Fermi level gradually shifts to the upper bound of the pseudogap when the Si content increases from zero to unity, signifying a gradual decrease in structural stability of the Ti3(Al1−xSix)C2 system as x increases. All Ti3(Al1−xSix)C2 compositions are brittle in nature in accordance with the Cauchy pressure, Pugh’s ratio and Poisson’s ratio. The Si content x increases the stiffness and decreases the thermal shock resistance of Ti3(Al1−xSix)C2. Ti3AlC2 is expected to be a promising thermal barrier coating material due to its low Debye temperature, lattice thermal conductivity and minimum thermal conductivity. Due to high melting temperature the solid solutions Ti3(Al1−xSix)C2 should also have potential applications in harsh environments. All compositions of Ti3(Al1−xSix)C2 are expected to be potential candidate coating materials for reduction of solar heating due to their minimum reflectivity above 45% in the visible region (1.8–3.1 eV).

Computational methods

Electronic structure calculations are carried out using the pseudopotential DFT method embodied in the Cambridge serial total energy package (CASTEP) code53. The Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA) is employed to model the exchange–correlation potential54. The interaction between electrons and ion cores is treated in the reciprocal space using the Vanderbilt-type ultrasoft pseudopotential55. For the Brillouin zone sampling a special k-point mesh of 13 × 13 × 2 in Monkhorst–Pack scheme is used56. BFGS minimization technique named after Broyden–Fletcher–Goldferb–Shanno is applied to optimize the geometry via minimizing the total energy and internal forces57. Pseudoatomic calculations for the valence and nearly valence electrons of Ti, Al, Si and C are performed using a planewave basis with an energy cutoff of 500 eV. The convergence tolerance for the total energy, maximum ionic force, maximum ionic displacement and maximum stress are set to 5.0 × 10–6 eV/atom, 0.01 eV/Å, 5.0 × 10–4 Å and 0.02 GPa, respectively. The present DFT method has been established for calculating the electronic structure of crystalline solids as described in previous studies3, 5.

The conventional unit cell of Ti3(Al1−xSix)C2 is modeled with the Virtual Crystal Approximation (VCA) technique as described in the code for mixing Si with Al at A-atomic sites, and the lattice parameters are obtained from the optimized cells. This technique allows one to mix different atoms, isotopes and oxidation states for a specific atomic site to be occupied randomly. The VCA technique has been previously applied successfully to study the disorder in some perovskites, silicates, ferroelectric ceramics and MAX phases18,19,24. This approach does not allow for any probable short-range order. It is assumed that a virtual atom occupies every potentially disordered site and extrapolates an averaged behavior between the real components. The VCA method ignores local distortions nearby the atoms. Therefore, in our case, there may be some energy difference between the actual Al1−xSix model and the VCA scheme. Ramer and Rappe58 carried out a comparative study for three different modifications of the 1:1 Pb(Zr,Ti)O3 ceramics. They found that the VCA results for structural aspect are highly consistent with those obtained in calculations. For total energies, both sets of results exhibit a negligibly small difference.

For optical properties and Mulliken atomic population calculations, a 5 × 1 × 1 supercell of Ti3AlC2 is constructed, from which 2, 4, 6, 8, and 10 Al atoms are replaced by Si atoms successively to obtain the composition Ti3(Al1−xSix)C2 with x = 0.2, 0.4, 0.6, 0.8, and 1.0, respectively. In this calculation, a k-point mesh of 2 × 9 × 1-grid with a plane-wave energy cutoff of 350 eV is applied.