Introduction

MAX phases are a family of over 70 synthesized ternary nitrides and carbides of general stoichiometry Mn+1AXn where n = 1, 2, or 3, M denotes early transition metals (TM), A represents A- group elements (mostly from group IIIA or IVA) and X is either nitrogen (N) or carbon (C)1,2,3,4. Resulting from their general formula, different groups of MAX phases are characterized as 211, 312, 413, 614, and so on5. Some MAX phases were discovered experimentally by Nowotny et al. about forty years ago6. In the early 1960s, the majority of MAX phases were discovered in a succession of experiments by Nowotny and his co-workers7. However, these discovered MAX phases did not receive adequate interest till the Barsoum and El-Raghy synthesized and fully characterized the bulk Ti3SiC2 MAX phase in 19968. Thereafter, interest in the layered ternary compounds increased rapidly9,10,11. Based on the web of science (WOS)12, to date, there are over 4,168 published papers on MAX compounds alone, with Ti3SiC2 having roughly half of the published works in the past six years13,14. MAX phase family is a large group of layered ternary carbides and nitrides that crystalizes into the hexagonal structure of spacegroup No. P63/mmc. Withthe characteristics of metallic as well as ceramics materials15, where each group member contains at least two forms of ionic, covalent, or metallic chemical bonds16. The MAX phases such as Ti3SiC2 and Ti3AlC2 are a 312 class of layered ternaries where the individual phases differ by the number of M-layers parting the A-layers in the 312-MAX phases17,18,19,20,21. These compounds combine some characteristics of metals like strong compressive strength, high fracturing strength, hardness, ductility, good electrical and thermal conductivity, high stiffness, damage tolerance, relatively low thermal expansion coefficient. Like ceramics they have outstanding thermal and chemical tolerance. . Furthermore, these compounds are considered as one of the best classes of materials for coating on steel surfaces in heavy liquid metals and as pump impellers. However, Ti3SiC2 and Ti3AlC2 are among the best-accepted representatives of the MAX phase compounds and are known as the best thermal conductors than titanium metal22,23,24,25,26.

First-principles approaches are widely employed to study the properties of MAX phases, for example, M2GaN (M = Ti, V and Cr)27, Ti2TlC, Zr2TlC, and Hf2TlC17,23, Ti3AlC2 and Ti2SiC220. Zhou et al.28 reported the distribution of charge density on the (1120) plane of Ti3AlC2, where robust directional Ti-C-Ti-C-Ti covalent bond chains were observed that linked to fairly weaker Ti–Al covalent bindings. In a similar study of electronic structure and bonding properties of Ti3AlC2, Wang and Zhou29 reported that the electrical conductivity of Ti3AlC2 decreases with increasing pressure, and over the whole pressure range, the material was found to exhibit elastic anisotropy. Son et al.30 have used density functional theory (DFT) to analyze the structural, elastic, and thermodynamic properties of Ti3SiC2 and Ti3AlC2 crystals. In order to discover the finite-temperature properties of these crystals, the vibrational, mechanical, quasi-harmonic contributions, and anharmonic adjustment to the total free energy of the systems were determined and extrapolated and the functions of electron localization, charge densities, electronic and vibrational densities have been studied.

Zhou and Zhimei investigated the electronic structure and chemical bonding in layered machinable Ti3SiC231. According to them, bonding within Ti3SiC2 is facilitated by metallic, covalent, and ionic bonding due to the strong Ti-C-Ti-C-Ti covalent bond strings in the structure31. In recent years, several studies have been carried out on the mechanical properties, and structural stabilities of Ti3SiC2 and Ti3AlC232,33,34 that reported their excellent structural properties that are suitable for many practical applications. Synchrotron x-ray diffraction measurements showed that Ti3SiC2 and Ti3AlC2 are stable materials under pressure from 0 to 61 GPa at room temperature35. Thermal stability of bulk Ti3AlC2 has been investigated36 within 1100–1400 °C, and hydrogen has been found to alter the properties and stability of the MAX phase. Analogous facts have also been noticed in the temperature range 1473–1673 K in bulk Ti3SiC2 in the hydrogen atmosphere and it was found that the dissociation of Ti3SiC2 was accelerated by hydrogen37.

Herein, we have investigated Ti3SiC2 and Ti3AlC2 using plane-wave pseudopotentials (PW-PP) approach in the framework of DFT. Since hardness varies from one material to another as commonly acknowledged by materials scientists, materials with Vickers hardness greater than 40 GPa are categorized as superhard38,39. We have achieved a result which by far characterizes Ti3SiC2 and Ti3AlC2 as superhard materials which we feel none of the studies conducted so far could address.

Result and discussion

Structural properties

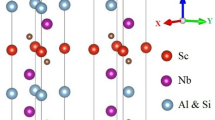
The layered ternary Ti3(Al1−nSin)C2 (n = 0, 1) compounds are based on the layers of hexagonally close-packed Si/Al and Ti layers with C occupying octahedral centers between the Ti layers as depicted in Fig. 1. The end phases could also be characterized as alternating stacking of two layers of a planar close-packed Si/Al and Ti6C octahedral layers. The Ti atom is found to be located at 4f. (0.33, 0.67, z), Al/Si atoms are positioned at 2b (0, 0, 0.25) whereas the atom of C is at 4f. (0.33, 0.67, z) Wyckoff positions. Figure 1 illustrates the crystal symmetries of the studied compounds and their computed structural parameters as well as the experimental results from available literature(s) are summarized in Table 1. The results of the equilibrium lattice constants, bulk modulus, and its pressure derivative are computed by fitting the obtained data of the equilibrium energy as well as volume to the second-order Birch-Murnaghan’s equation of state (EOS)40. The obtained results showed the reasonability of our calculations.

Figure 1
figure 1

Crystal structure of (a) Ti3AlC2, (b) Ti3SiC2 MAX phase compounds.

Full size image
Table 1 Calculated equilibrium lattice parameters a, c, c/a ratio, volume, V, bulk modulus Bo, and its pressure derivative\({, B}_o^{\mathrm{^{\prime}}}\) and values from the literature.
Full size table
$$ ~E\left( V \right) = E_{o} \frac{9}{{16}}B_{o} \left[ {\left( {4 - B_{o}^{'} } \right)\frac{{V_{o}^{3} }}{{V^{2} }} - \left( {14 - 3B_{o}^{'} } \right)\frac{{V_{o}^{{7/3}} }}{{V^{{4/3}} }}\left( {16 - 3B_{o}^{'} } \right)\frac{{V_{o}^{{5/3}} }}{{V^{{2/3}} }}} \right] $$
(1)

One can easily note that the difference between our obtained results and experimental data of equilibrium lattice parameters is less than 1%, showing that our results obtained at the level of the Perdew-Burke-Ernzerhof (PBE) type of generalized gradient approximations functional are sufficiently reliable. In Table 1, the bulk modulus of Ti3SiC2 is higher than that of Ti3AlC2, showing that Ti3SiC2 is harder than Ti3AlC2.

Electronic properties

Figure 2 demonstrates the band structures and total density of states (TDOS) computed along the high symmetry points in the brilluoin zone (BZ) using the equilibrium lattice parameters. It is seen that both valence bands and conduction bands overlap significantly resulting in no energy gap at the Fermi level. Thus, the studied compounds demonstrate metallic character which is a common feature of the MAX phase materials. However, there are more valence electrons in the Ti3SiC2 unit cell than in Ti3AlC2. This gives rise to the further occupation of the bonding states near the Fermi level. The substitution of Si by Al in Ti3AlC2 presents additional valence electrons per atom, and consequently, the Fermi level is moved to a higher energy level. This suggests that the increased extra valence electrons fill in the Si/Al-Ti p-d hybridized bonding states as well as the metal to metal d-d consequential bonding.

Figure 2
figure 2

Band structures and TDOS of (a) Ti3SiC2, (b) Ti3AlC2 MAX phase compounds.

Full size image

Accordingly, the filling of the bonding orbitals rises the strength of the bond and thereby increasing the bulk moduli. The energy band also exhibits a highly anisotropic character along with lesser c-axis energy dispersion. The anisotropy of the band structure near and below the Fermi level implies that, for single crystals, both Ti3SiC2 and Ti3AlC2 are conductors and anisotropic, and electrical conductivity is lowered along c direction than the ab- plane similar to the observed trend in the literature28.

The investigated total densities of states (TDOS) plot for Ti3SiC2 and Ti3AlC2 presented in Fig. 2 points out that the peak structures and corresponding heights of the peaks are equivalent, signifying resemblance in chemical bonding. The TDOS per unit cell at the Fermi level for Ti3SiC2 and Ti3AlC2 are 4.029 and 6.855 states/eV, respectively. Therefore, there is an increasing trend in the DOS at the Fermi level with an increasing number of valence electrons of the transition metals showing that the transition metal bands play a dominant role in the TDOS and their electrical transport properties. Analysis of bonding properties is obtained from the PDOS of each contributing element in Fig. 3. Here, the width of Al-3 s and Si-3 s states are wider for each one than that of the C-2 s state. With several less contributing peaks in the Al/Si-are due to 3 s states. The Al/Si-3 s energy states show that there are s-p interactions in Al/Si, i.e. close-packed layer of Al/Si atoms are bonded through s-p interactions. For the energy range -12 eV to -9.4 eV in the valence bands of both Ti3SiC2 and Ti3AlC2, there is a high degree of hybridization of C-2p with Ti-3d states, which suggests covalent bonding between them. Hence the chemical stability is largely attributed to the p-d hybridization. Therefore, the Ti-3d and C-2p hybridization is a driving bonding force in Ti3SiC2 and Ti3AlC2, similar to bonding properties in some 312 MAX phases like Ti3SnC2 and Ti3GeC242,43.

Figure 3
figure 3

Calculated PDOS of (a) Ti3SiC2 and (b) Ti3AlC2 MAX phases.

Full size image

Elastic properties

Investigations of elastic constants are vital for applications related to the mechanical properties of solids. They provide information on stability, bonding, ductility, brittleness, anisotropy, compressibility, Vicker’s hardness, and stiffness of solids44,45. For hexagonal crystals structures, five independent elastic constants (\({C}_{11}\), \({C}_{12}\), \({C}_{13}\),\({C}_{33}\), \({C}_{44}\)) are required. Table 2 summarizes our computed results of the five independent elastic constants of Ti3SiC2 and Ti3AlC2 alongside available experimental and theoretical data.

Table 2 Computed elastic constants Cij (GPa) alongside experimental and theoretical results.
Full size table

A stable hexagonal crystal must satisfy the following Born-Huang stability criteria46;

$${C}_{11}>0; {C}_{11}-{C}_{12}>0; {C}_{44}>0; \left({C}_{11}+ C_{12}\right){C}_{33}-{2C}_{13}^{2}>0$$
(2)

Table 2 demonstrates that the computed results of the independent elastic constants for Ti3SiC2 and Ti3AlC2 MAX phase compounds satisfy the mechanical stability criteria which signify that all the compounds are mechanically stable. It is also well known that elastic constants C11, and C33 shows linear compression resistances along a and c directions, respectively, whereas C12, C13, and C44 are related to the shape elasticity. Consistent with Table 2, the value of C11 is higher than C33 for both Ti3SiC2 and Ti3AlC2 compounds which agrees well with literature results.

From the computed elastic constants, several polycrystalline elastic moduli comprising, Bulk, Shear, Young moduli, and Poisson’s ratio were evaluated using Voigt48, Reuss49, and Hill50 approximations. It is assumed that, in the Voigt scheme, the strain is uniform all along the polycrystalline materials aggregating to external strain. By following this approach, for the hexagonal lattices, the Voigt shear modulus (GV) and Reuss shear modulus (GR) are expressed as:

$${G}_{V}= \frac{1}{15}\left\{2{C}_{11}-{C}_{12}+{C}_{33}-{2C}_{13}\right\}+\frac{1}{5}\left\{2{C}_{44}+\frac{1}{2}\left( {C}_{11}-{C}_{12}\right)\right\}$$
(3)
$${G}_{R}=\frac{5}{2}\left\{\frac{\left[\left[\left({C}_{11}+{C}_{12}\right){C}_{33}-2{C}_{13}^{2}\right]{C}_{44}{C}_{66}\right]}{\left[3{B}_{V}{C}_{44}{C}_{66}+\left[\left({C}_{11}+{C}_{12}\right){C}_{33}-2{C}_{13}^{2}\right]\left({C}_{44}+{C}_{66}\right)\right]}\right\}$$
(4)

And Voigt bulk modulus (BV), Reuss bulk modulus (BR) by:

$${B}_{V}= \frac{1}{9}\left\{2\left({C}_{11}+ {C}_{12}\right)+{C}_{33}+4{C}_{13}\right\}$$
(5)
$${B}_{R}= \frac{\left({C}_{11}+{C}_{12}\right){C}_{13}-2{C}_{13}^{2}}{{C}_{11}+ {C}_{12}+2{C}_{33}+4{C}_{13}}$$
(6)

Hill showed that Voigt/Reuss averages give upper and lower bounds, and therefore, proposed that real effective moduli can be approximated by the arithmetic mean of the two bounds51. Thus, using Hill’s approximations

$$B=\frac{1}{2}\left({B}_{R}+{B}_{V}\right),\quad G=\frac{1}{2}\left({G}_{R}+{G}_{V}\right)$$
(7)

We have also computed \(Y\), and \(\eta \), which are commonly evaluated for polycrystalline materials to study their hardness. Both \(Y\) and \(\eta \) are defined by the following expressions as;

$$Y=\frac{9BG}{3B+G} , \quad\eta =\frac{3B-2G}{2\left(3B+G\right)}$$
(8)

The computed Bulk modulus, Young’s modulus, Shear moduli, and Poisson’s ratio of both Ti3SiC2 and Ti3AlC2 as defined in Eqs. (3)–(8) are listed in Table 3. The calculated values for the bulk modulus of Ti3SiC2 and Ti3AlC2 are 139 GPa and 182 GPa respectively. These values agree well with the reported value by Gray et al.47, with less than 13% and 7% deviation respectively for Ti3AlC2 and Ti3SiC2. Moreover, our results for Shear modulus of 87 GPa for Ti3AlC2 although are lower than the reported experimental value in Table 3, the results of Ti3SiC2 of 121 GPa are in good agreement with the reported value. From comparing Tables 1 and 3, it can be seen that the calculated value of B obtained from the single crystal elastic constants summarized in Table 3 has approximately the same value as the one obtained from the data fitting in the Murnaghan’s equation of state (Table 1). This indicates the accuracy and reliability of our computed elastic constants for both Ti3SiC2 and Ti3AlC2 MAX phase compounds.

Table 3 Computed bulk modulus B (GPa), Young modulus Y(GPa), shear modulus G (GPa), Poisson’s ratio η, compressibility B−1 (GPa)−1, Pugh’s ratio (B/G), Cauchy pressure \({C}_{c} \mathrm{(GPa)},\) anisotropic factor-A and Vicker’s hardness Hv.
Full size table

Following the Pugh ratio, \(B/G\) shows the brittle or ductile character of materials. Pugh’s critical value is 1.75. The calculated ratio B/G for Ti3AlC2 and Ti3SiC2 are 1.60 and 1.56, respectively, which are less than Pugh’s critical value. As such, these compounds have a brittle feature which agreed well with the result given in Table 352. Cauchy relation defined as: \({C}_{c}={C}_{13}-{C}_{44}\), is another parameter signifying ductility or brittleness of a material. Positive values of \({C}_{c}\) shows ductility otherwise the material is brittle53. The evaluated \({C}_{c}\) of the ternaries are -44 and -28 GPa respectively. From these values, one can conclude that the studied materials are brittle in nature which confirmed the Pugh’s result. Consequently, the brittle nature of Ti3AlC2 and Ti3SiC2 can be related to their ceramic character.

Young’s modulus (Y) measures the stiffness of a material. The higher the Y, the stiffer a material is. Our result presented in Table 3 shows that there is good agreement with the reported values of 215 GPa and 297 GPa for Ti3AlC2 and Ti3SiC2, respectively. Information about the bonding forces can be obtained via Poisson’s ratio (η). The\( \left(\eta \right)\) for Ti3AlC2 and Ti3SiC2 are 0.24 and 0.23 respectively, which shows the interatomic forces within studied materials are central since upper and lower limits of the Poisson’s ratio is \(0.5\) and \(0.25\) respectively, and the calculated values fall within the two limits. Our results are closer to the experimental value of 0.178 for Ti3AlC2 and 0.248 for Ti3SiC252. We have further calculated the Vickers’ hardness Hv54 of studied compounds. Vickers’s hardness is another key mechanical property of solids that explains stability, which is predicted using Eq. (9). It is reported that solids with Vickers hardness HV > 40 GPa38 are graded as super hard solids. The calculated Hv of Ti3AlC2 and Ti3SiC2 MAX phase compounds are 40.28 GPa, and 46.75 GPa respectively (Table 3). Therefore, these crystals, have an excellent ability to withstand dents or scratches.

$${H}_{V}=0.92{\left(\frac{B}{G}\right)}^{1.3137}{G}^{0.708}$$
(9)

Method

Ab initio calculations were used to investigate the elastic, and electronic properties of Ti3SiC2 and Ti3AlC2 using PW-PP as implemented in Quantum Espresso55. Generalized gradient approximation (GGA) parametrized by Perdew-Burke-Ernzerhof (PBE) is used to treat exchange and correlation (XC) energy56. The core ion and valence electrons interactions were described using ultrasoft-pseudopotentials (UPP). A 600 Ry kinetic energy cut-off of the plane wave is used in the calculations. The electronic configurations: 3s2, 4s2, 3p6, 3d2 for Ti, 3s2, 3p2 for Si, 3p1, 3s2 for Al and 2s2, 2p2 for C were considered for the valence electrons. For the Brillouin zone (BZ) integration, 12 × 12 × 12 k-points mesh was generated using the Monkhorst–Pack scheme57. These parameters were found to be adequate to converge total energies up to 10–8 eV. Both studied materials were fully relaxed in terms of cell parameters and atomic positions. Analysis of independent elastic constant \(({C}_{ij})\) were performed using thermo_pw45. \({C}_{ij}\) delineates response of materials to macroscopic stress. In computing elastic constants, a small strain, e is applied to a material and the variation of total energy per volume, U of the material is obtained58:

$$U=\frac{\Delta E}{{V}_{0}}=\frac{1}{2}\sum_{i}^{n}\sum_{j}^{m}{C}_{ij}{e}_{i}{e}_{j}$$
(10)

where \({V}_{0}\) and \(\Delta E\) represent the equilibrium volume and the difference between the initial and deformed total energy of the system respectively. The hexagonal Ti3SiC2 and Ti3AlC2 MAX phase compounds are characterized by five independent elastic constants which include \({C}_{11}\), \({C}_{12}\), \({C}_{13}\),\({C}_{33}\) and \({C}_{44}\). Therefore, the elastic matrix of the hexagonal system is written as59,60;

$${C}_{ij}=\left[\begin{array}{cccccc}{C}_{11}& {C}_{12}& {C}_{13}& .& .& .\\ .& {C}_{11}& {C}_{13}& .& .& .\\ .& .& {C}_{33}& .& .& .\\ .& .& .& {C}_{44}& .& .\\ .& .& .& .& {C}_{44}& .\\ .& .& .& .& .& .\end{array}\right]$$
(11)

Conclusion

In this work, the structural stability, electronic, and mechanical properties were investigated using ab-initio calculations. The complete set of independent elastic constants Cij, shear modulus, bulk modulus, Poisson’s ratio, and Young’s modulus were calculated. Our results showed that the studied ternaries are mechanically stable and are super hard materials with Vicker’s hardness as large as 46.75 GPa and 40.28 GPa for Ti3SiC2 and Ti3AlC2 respectively. The investigated electronic band structures, TDOS, and PDOS showed the metallic behavior of these compounds. In Ti3SiC2, the top of the VB and bottom of the CB were found to be dominated by the Si-3p, C-2p, and Ti-3d energy states while for the Ti3AlC2 the top and bottom of VB and CB were respectively found to be shaped by Al-3p, C-2p, and Ti-3d orbitals. We expect that our findings will provide suitable guidance for experimental and theoretical studies on these interesting MAX phases.