Introduction

Control charts are useful tools for fault detection1. Shewhart chart, CUSUM chart and EWMA chart are most popular tools in statistical process control. These control charts are efficient and fruitful for fault diagnosis in practical applications. Most control charts that need observations are univariate and usually assume that the observation follows a known gaussian distribution.

In real life, we usually process multivariate or high-dimensional variables rather than univariate variables. The monitoring of high–dimensional data in a timely manner has become increasingly important in quality control. Hotelling2 proposed a T-squared control chart for multivariate process, which assumes that the dataset distributions are multivariate normal distribution. Both the parameters of mean vector and variance matrix are known. Based on T2 statistics, Lowry et al.3 proposed a multivariate CUSUM chart. Furthermore, Sullivan and Woodall4 provided a change–point chart for detecting a shift of the location parameter, the scale parameter.

However, statistical process control is a challenge when the underlying distribution and the magnitude of changes are both totally unknown. For the situation of a multivariate process with an unknown distribution, Yue and Liu5, from the point of Mahalanobis data depth, introduced a chart for monitoring processes for multivariate process. Data depth is efficient and totally nonparametric. However, the computational complexity is high as the number of variables grows and may influence the performance of detection of a chart. In addition, the covariance matrix of the data depth method is constant5. Therefore, the method may be unsuitable when the covariance matrix in a process is not stable. Zou and Tsung6 proposed a new multivariate EWMA chart to detect location parameters. The chart is affine-invariant, and its controlled run length distribution is the same for the class of distributions with elliptical directions.

Some strictly distribution–free rank–based methods have been developed to increase the efficiency in detecting a nonparametric process7,8,9. The computation speed of these rank–based methods is fast, and the methods are easy to implement. However, all of these methods focus on a univariate process. In our article, we introduce a new nonparametric multivariate EWMA chart based on rank method, which is combined with the Hotelling T2 statistic for a multivariate process. This method is completely distribution–free, and it is easy to implement in applications. Moreover, the covariance matrix of observations keeps being updated as new observations arrive. Additionally, the computation load is very light.

For multivariate or high-dimensional statistical process control, location parameter shifts sometimes occur in only one or a few characteristics in a process. We want to detect these shifts quickly, accurately and to identify the shifted location parameter components. Consider this issue, fruitful nonparametric control charts have been introduced in the literature. Qiu and Hawkins10 and Hawkins11 constructed a new multivariate statistical process control chart and indicated that proposed chart was more efficient than the T2 control chart when a shift occurred in only one characteristic. However, the shift of a process is usually unknown and may occur in several highly correlated variables. To address this issue, in the context of a process where the location parameter often changes in a few number of variables, Zou and Qiu12 proposed a useful multivariate statistical process control chart by using the LASSO tool. In addition, inspired by Zou and Tsung, Liang et al.13 came up with a new multivariate EWMA chart to monitor sparse mean changes. In our paper, the proposed method is designed to detect sparse mean changes, and the results shows that this method performs relatively better in applications.

Previous studies showed that the multivariate control chart could be useful for biosurveillance. Rogerson and Yamada14 proposed a multivariate cumulative sum approach to detect the change in spatial patterns and applied it to a county-level breast cancer datasets. Their results suggested that the proposed chart for multivariate process performed relatively better compared with the univariate method when shifts occurred in many regions. Abdollahian and Hayati Rezvan15 applied a multivariate EWMA control chart to monitor patient’s progress after cardiac surgery, in which the proposed multivariate EWMA chart can detect an out-of-control signal that was missed by the univariate EWMA charts. This is because that the correlations between charting statistics are ignored in univariate chart. Then the univariate chart may give a misleading indication when such correlation is considerably high.

The structure of this paper is organized as follows: in Section 2, the rank–based method is given, and a nonparametric chart for online monitoring is provided. A simulation of this control chart is presented in Section 3. Real data are studied to illustrate the performance of the proposed control chart in Section 4. Finally, some conclusions are presented in Section 5.

Model

EWMA control chart

The EWMA control chart has good properties for control applications. Lucas and Saccucci16 studied the performance of EWMA and CUSUM charts. In their paper, the EWMA chart has relatively better performance for small shifts with an appropriate smoothing parameter. The EWMA control chart is first introduced for univariate variables. The EWMA control chart is easy to construct and implement, and it is based on the following statistic:

$${Z}_{i}=\lambda {X}_{i}+(1-\lambda ){Z}_{i-1},\,0 < \lambda \le 1,$$

Zi is the EWMA statistic, where the starting value is Z0 = 0, and λ is a smoothing parameter. Xi represents the observations in a process. The EWMA chart corresponds to a Shewhart control chart when λ = 1. The weight of the historical data is decided by the magnitude of the smoothing parameter. A process is considered out-of-control (OC) whenever Zi falls outside the range of the control limits.

Rank–based methods

A rank–based method is first given for a one–dimensional process. Liu et al.9 introduced the rank–based method and assumed that independent observations, Xi, follow the model below:

$${X}_{i} \sim \{\begin{array}{cc}F(X,{\mu }_{0}), & if\,i=1,2,\cdots ,\tau ,\\ F(X,{\mu }_{1}), & if\,i=\tau +1,\tau +2,\cdots ,\end{array}$$

where μ0 is the in-control (IC) location parameter, and μ1 is the OC location parameter. τ is the unknown change point. F is an unknown continuous distribution function. Let Ri denote the i th sequential rank; Liu et al.9 presented the formula for the rank of Xi among X1, X2, …, Xi, …, Xn as follws:

$${R}_{i}=\mathop{\sum }\limits_{j=1}^{i}\,I\{{X}_{i}\ge {X}_{j}\}.$$

The standardized sequential rank was defined as

$${R}_{i}^{\ast }=\frac{{R}_{i}-E{R}_{i}}{\sqrt{Var{R}_{i}}}(i\ge 2),$$

where

$$E{R}_{i}=\mathop{\sum }\limits_{r=1}^{i}\,r\times P({R}_{i}=r)=\mathop{\sum }\limits_{r=1}^{i}\,r\times \frac{1}{i}=\frac{i(i+1)}{2}\times \frac{1}{i}=\frac{i+1}{2},$$
$$Var{R}_{i}=E({R}_{i}^{2})-{(E({R}_{i}))}^{2}=\mathop{\sum }\limits_{r\mathrm{=1}}^{i}\,{r}^{2}\times P({R}_{i}=r)-{(\frac{i+1}{2})}^{2}=\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}\mathrm{.}$$

\({R}_{i} \sim U[1,\,i]\). Therefore,

$$({R}_{i}-\frac{i+1}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}} \sim U[(1-\frac{i+1}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}},(i-\frac{i+1}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}}]\mathrm{.}$$

Then,

$$(1-\frac{i+1}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}}=(\frac{1-i}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}}=-\sqrt{\mathrm{3((}i-\mathrm{1)/(}i+\mathrm{1)}},$$
$$(i-\frac{i+1}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}}=(\frac{i-1}{2})/\sqrt{\frac{(i+\mathrm{1)(}i-\mathrm{1)}}{12}}=\sqrt{\mathrm{3((}i-\mathrm{1)/(}i+\mathrm{1)}}\mathrm{.}$$

Therefore, the distribution of Ri* is defined in the interval

$$[-\sqrt{\mathrm{3((}i-\mathrm{1)/(}i+\mathrm{1)}},\sqrt{\mathrm{3((}i-\mathrm{1)/(}i+\mathrm{1)}}].$$

The asymptotic distribution of Ri* is U(\(-\sqrt{3}\), \(\sqrt{3}\)) as i → ∞.

In the context of a multivariate process, it is supposed that there are m independent observations from an unknown multivariate continuous distribution with dimensionality p. That is, Yi = (Y1,i,Y2,i, …, Yp,i)′, i = 1, 2, …, m. There are p characteristics to be examined that we are interested in. For a set of variables, Yj,1, Yj,2, …, Yj,m, j = 1, 2, …, p, which represents the j th characteristic with m observations, the rank–based method can be used to construct statistics. When the observations are p-dimensional, the i th observations are Yi = (Y1,i, Y2,i, …, Yp,i)′. For the j th component, Yj,i, Rj,i* denote the i th standardized sequential rank with the arrival of the j th component Yj,i. Therefore, the vectors Qi = (R1,i*, R2,i*, …, Rp,i*)′ can be obtained. In addition, each component Rj,i* follows the same uniform distribution as Ri*. Then, the EWMA statistics can be constructed, which are based on T2 statistics. The EWMA statistics are given by

$${Z}_{i}=R{Q}_{i}+(I-R){Z}_{i-1},$$

where R = diag(λ1, λ2, …, λk, …, λp), <λk ≤ 1 represents the smoothing parameter. I represents the p-dimensional identity matrix. If there is no a priori information given, different smoothing parameters are needed for different components; then, λ1 = λ2 = ··· = λk = ··· = λp are used, and the starting value is Z0 = (0, 0, …, 0)′. The process is considered to be OC if a manufacturing or business process is in a state of uncontrollable (i.e. ZiΤΣZi−1Zi > L), where L is the upper control limit. And the covariance matrix of Zi is as follows:

$${\varSigma }_{{Z}_{i}}=\mathop{\sum }\limits_{k=1}^{i}\,R{(I-R)}^{i-k}\varSigma {(I-R)}^{i-k}R\mathrm{.}$$

In particular, ΣZi = (1−(1−λ)2i)λ/(2−λ)Σ when λ1 = λ2 = ··· = λk = ··· = λp = λ. λ is a fixed value. Usually, we take the limit form, ΣZi = λ/(2−λ)Σ. Σ, the covariance matrix of Qi, is estimated from samples in practice.

Simulation

In the art of research, fruitful distribution–free control charts have been introduced. If a chart IC run–length distributions are the same to every continuous distribution17, we call this chart is nonparametric or distribution-free. We discuss the choice of parameter by using the multivariate normal distribution. This indicates that the determine of parameters are still valid when a series of observations obey other distributions. Therefore, we consider the i th observation, Xi, is collected as time goes by using the following relational model:

$${X}_{i} \sim \{\begin{array}{cc}N({\mu }_{IC},{\varSigma }_{IC}\mathrm{),\ } & i=\mathrm{1,}\,\mathrm{2,}\cdots ,\tau ,\\ N({\mu }_{OC},{\varSigma }_{IC}), & i=\tau +\mathrm{1,}\,\tau +\mathrm{2,}\cdots ,\end{array}$$

where

$${\mu }_{IC}=(0,0,0),\,{\varSigma }_{IC}=(\begin{array}{ccc}1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\end{array})\,and\,{\mu }_{OC}=(\delta ,0,0).$$

And α is the probability of a type I error and β is the probability of a type II error. For a fair comparison, we usually fix α and compare β. A small β is considered better. The average run length (ARL) is the number of points that, on average will be plotted on a control chart before an OC signal. If a manufacturing or business process is IC:

$$AR{L}_{0}=1/\alpha .$$

If the process is considered OC:

$$AR{L}_{1}=1/(1-\beta ).$$

Therefore, we fix IC ARL, ARL0 and compare OC ARL, ARL1. A small ARL1 is considered better.

Meanwhile, inspired by Han and Tsung18, we consider the relative mean index (RMI) values to evaluate the average performance of these charts for detecting a range of parameter changes, which are given as following:

$${\rm{RMI}}=\frac{1}{m}{\sum }_{i\mathrm{=1}}^{m}\,\frac{AR{L}_{{\delta }_{X}}-MAR{L}_{{\delta }_{X}}}{MAR{L}_{{\delta }_{X}}},$$

where m is the number of shifts that we considered. When detecting a certain shift δX, ARLδX denotes as the OC ARL of these given charts. And MARLδX is the smallest OC ARL among all the OC ARL values of these charts when detecting a certain shift δX. The RMI calculates the average of all the detection efficiency values18. A control chart with a relatively smaller RMI value is regarded as relatively better detection efficiency.

We suppose that there are 1000 independent and identically distributed historical (reference) observations. X1, X2, …, X1000 are 1000 random observations from N(μ0,Σ0). To make a fair comparison, all of these control charts have the same IC zero–state ARL, which is equal to 500. It should be note that zero-state run lengths refer to the run lengths of control charts initialized at the target value16. When the process goes OC, a chart is considered as a better detection efficiency with a small ARL. The ARLs of these EWMA methods with λ = 0.03 for a range of shifts are presented in Table 1. EWMA1 represents the rank-based EWMA scheme, and EWMA2 represents an EWMA control chart based on the Mahalanobis depth method5. We also provide simulation studies with the non-diagonal covariance matrix

$${\varSigma }_{1}=(\begin{array}{ccc}9 & 8 & 8\\ 8 & 9 & 8\\ 8 & 8 & 9\end{array}),$$
Table 1 ARL comparisons for the EWMA control chart under N(μ0,Σ0) with a zero–state ARL = 500.
Full size table

The ARLs of the EWMA scheme with λ = 0.03 for a range of shifts under N(μ0,Σ1) are presented in Table 2. In addition, the detection performance of these charts under a bivariate Weibull distribution, LBVW(θ1, θ2,α,ρ) are shown in Table 3. θ1 and θ2 are the scale parameter. α is the shape parameters. ρ is the correlation coefficient. When a process is IC, \(({X}_{1},{X}_{2}) \sim LBVW({\theta }_{1},{\theta }_{2},\alpha ,\rho )\). \(({X}_{1},{X}_{2}) \sim LBVW({\theta }_{1},{\theta }_{2},\alpha +{\delta }_{X},\rho )\) when the process is OC. Tables 1–3 provide the ARL of the EWMA1 and EWMA2 control charts for a range of shifts δX. Tables 1–3 show that the EWMA1 control chart has a relatively better performance for detecting small shifts. EWMA2 has a better performance for detecting large shifts. On the whole, EWMA1 has a relatively small RMI.

Table 2 ARL comparisons for the EWMA control chart under N(μ0,Σ1) with a zero–state ARL = 500.
Full size table
Table 3 ARL comparisons for the EWMA control chart under LBVW(1, 1, 1, 0.5) with a zero–state ARL = 500.
Full size table

Table 4 presents the simulation results under N(μ2,Σ2), where μ2 = (0, 0, 0, 0, 0, 0) and Σ2 is 6 × 6 indentity matrix. Table 4 shows that EWMA1 still performs better. Sometimes, we encounter the case that observations follow block-diagonal correlation structures. Therefore, we provided ARL comparisons for observations follow a block-diagonal correlation structures, which presented in Table 5. Where μ3 = (0, 0, 0, 0) and

$${\varSigma }_{3}=(\begin{array}{cccc}1 & 1 & 0 & 0\\ 1 & 3 & 0 & 0\\ 0 & 0 & 1 & 1\\ 0 & 0 & 1 & 2\end{array})\mathrm{.}$$
Table 4 ARL comparisons for the EWMA control chart under N(μ2,Σ2) with a zero–state ARL = 500.
Full size table
Table 5 ARL comparisons for the EWMA control chart designed to detect a shift under N(μ3,Σ3) with a zero–state ARL = 500.
Full size table

Table 5 shows the proposed methods performs relatively better. In addition, the proposed control chart based on ranks of data is a nonparametric method without assuming normal or Poisson distribution for the data. To investigate the performance of the proposed method for Poisson data, we conducted an additional simulation study under multivariate Poisson distribution. Results in Table 6 showed that the proposed methods (EWMA1) still had a better performance in terms of the OC ARL and RMI.

Table 6 ARL comparisons for the EWMA control chart designed to detect a shift under multivariate Poisson(θ1 + δX, θ2, θ0) with a zero–state ARL = 500, where (θ1, θ2, θ0) = (0.5, 0.6, 0.2).
Full size table

In addition, we also provide the computing time of the EWMA1 and EWMA2 control charts. From Fig. 1, EWMA1 has relatively shorter computing time compared to that of EWMA2. Therefore, the proposed EWMA control chart is chosen, which is based on rank methods, for monitoring in this paper.

Figure 1
figure 1

Computing time of the EWMA1 and EWMA2 charts for a range of shifts.

Full size image

Analysis of Japanese Data

Data source

That is the case, with the Japanese influenza data19, which cover 6 regions in Japan. These regions include Gunma, Chiba, Tokyo, Ishikawa, Nagano, and Osaka. Influenza data analysis is a very important issue today20,21. Simultaneous monitoring of flu break–outs in multiple regions is an important topic in epidemiology. Influenza is an acute contagious disease caused by a virus19. The Japanese influenza data are used to illustrate the proposed control chart. Time–series data of the weekly incidence of influenza in Japan are used from January 2000 through December 2011. To evaluate the incidence data (see “Influenza Dataset” in Supplementary Information), we conduct spectral analysis, which is useful for investigating the periodicities of shorter time series, such as that of the incidence data used in the present study.

The Japanese influenza data are presented in Fig. 2. A quantile–quantile (Q–Q) plot of each region that includes 782 historical observations is presented in Fig. 3. Figure 3 suggests that the normality assumption for the influenza data is invalid.

Figure 2
figure 2

The Japanese influenza data.

Full size image
Figure 3
figure 3

The corresponding normal Q-Q plot.

Full size image

The correlation of six regions as shown in Fig. 4, for a total of C62 = 15 lines. Figure 4 shows that the cross-correlation is not stable. Therefore, we update the covariance matrix with the arrival of new observations. It should be noted that the covariance matrix Σ is updated, as presented in section 2.2.

Figure 4
figure 4

Correlation of six regions.

Full size image

Data analysis

In this section, a multivariate control chart is used to monitor the incidence of influenza in six regions which may have a certain correlation. Ignoring the correlation and using several univariate charts could lead to biased conclusions. For example, the univariate chart statistic may result in unnecessarily frequent out-of-control signals when the process is actually in control and may not detect the change when the process becomes out of control3.

In the past few decades, many researchers have studied spectral analysis22. In addition to the obvious annual cycle of influenza epidemics, the longer–term incidence patterns are important for interpreting the mechanism of influenza epidemics. The method proposed by Sawada et al.23 is a combination of spectral analysis and non–linear least squares fitting (LSF) for fitting analysis. Spectral analysis is a useful tool to investigate the periodicities of a short time series, and the formulations of the LSF curve are related to the research of Sawada et al.

Spectral analysis is used identify the interepidemic period of influenza epidemics in Japan (see “Computing Code” in Supplementary Information). Based on spectral analysis, the trend of the incidence data is determined. The procedure comprises the following 3 steps. In step I, the influenza data (standardized datasets) are preprocessed. In step II, the temporal behavior of the interepidemic period is investigated. Then, LSF is used for the fitting analysis. This trend is then removed by subtracting the LSF curve from the data, thereby yielding the residual time–series data. In step III, the obtained residual time–series datasets are analysed.

The vertical coordinates of Fig. 5 represents the power spectral density (PSD). Figure 5 indicates that the numbers of the maximum entropy method (MEM) spectral periods. From Fig. 5 and the processed data, we find that the power has a large magnitude at a frequency of 0.035 (1/week), and there is a second peak at a frequency of 0.019 (1/week). A large magnitude indicates that a large portion of the amplitude of the incidence data is expressed as a wave that repeats itself every year. Spectral analysis has enabled us to identify multiple periodicities for the interepidemic period of influenza epidemics (1- and 0.5-year periods). The residual time–series data are relevant.

Figure 5
figure 5

Spectral analysis of the influenza data series.

Full size image

For residuals data, Table 7 presents the results of Shapiro-Wilk test and Kolmogorov-Smirnov test for normality. The p-values are smaller than 0.05, indicating that the data are non-normally distributed. Therefore, a nonparametric control chart could be more appropriate than those based on normality assumption. Moreover, a first order autoregressive model (AR(1)) is used to analyze the sequence correlation. Table 8 shows that sequences are highly correlated. Thus, the first order difference is employed to reduce the sequence correlation (see results in Table 9). Then the differential data can be used to illustrate the proposed method.

Table 7 Shapiro-Wilk test and Kolmogorov-Smirnov test for normality.
Full size table
Table 8 The coefficients of AR(1) for residuals data.
Full size table
Table 9 The coefficients of AR(1) for residuals data after the first order difference.
Full size table

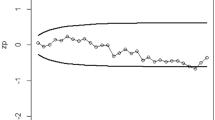
The EWMA1 control chart of the residual data series is presented in Fig. 6. Figure 6 shows that EWMA statistics fall outside the range of the control limits in 2003, 2006, 2009. SARS jumped simultaneously from a village in China to two cities on opposite sides of the world, Singapore and Toronto, in 2003. H5N1 outbreaks in poultry peaked in 2006, and the highly pathogenic H5N1 avian influenza virus spread to affect wild or domestic birds in 17 new countries in Africa, Asia, Europe, and the Middle East. The H1N1 influenza pandemic continued to spread in 2009. From Fig. 7, the four peaks occurred at approximately the 160th case (2003-1-19), 366th case (2006-12-31), 509th case (2009-9-27), and 596th case (2011-5-29), respectively. The signal of alarm appeared for the 159th case (2003-1-12), 363th case (2006-12-10), 502th case (2009-8-9), suggesting that the proposed method can provide early detection of influenza epidemics.

Figure 6
figure 6

EWMA1 control chart.

Full size image
Figure 7
figure 7

EWMA control chart based on data depth.

Full size image

We provide the performance of EWMA2 by using Japanese influenza data (Fig. 7). It can be observed that the EWMA2 chart shows an inconsistent trend with the result in practice (the charting statistics indicate that the six regions are almost at the epidemic level after 32 cases). This may be caused by the constant covariance setting in EWMA2. Hence, updating the covariance between the six regions could be important in correctly detecting an epidemic of influenza.

We also presented six single univariate control charts for Japanese influenza data in Fig. 8. The univariate chart statistic gave unnecessarily frequent out-of-control signals when the process is actually in control. Specifically, the first out-of-control signal of six regions occurred approximately at the 30th case, the 61th case, the 42th case, the 24th case, the 27th case, and the 17th case, respectively. However the multivariate chart may suggest a in-control state, indicating that ignoring the correlation between regions in biosurveillance may give an unexpected high rate of false alarm.

Figure 8
figure 8

Six single univariate control charts for Japanese influenza data.

Full size image

Conclusions

This paper provides a new EWMA control chart based on rank methods for a multivariate process. The performance of an EWMA control chart based on rank methods and Mahalanobis depth are compared. The EWMA control chart based on rank methods has a relatively better performance for detecting small shifts. Finally, Japanese influenza data are also provided to illustrate the proposed control chart. Spectral analysis is first conducted to investigate the periodicities of shorter time series, and then non–linear least squares fitting is used for fitting analysis. The residual data series are obtained, and the residual data series are monitored. The Japanese influenza data example shows that the proposed control chart has relatively better performance for detecting process changes.