Abstract
Molecular based spin-1/2 triangular lattice systems such as LiZn2Mo3O8 have attracted research interest. Distortions, defects, and intersite disorder are suppressed in such molecular-based magnets, and intrinsic geometrical frustration gives rise to unconventional and unexpected ground states. Li2AMo3O8 (A = In or Sc) is such a compound where spin-1/2 Mo3O13 clusters in place of Mo ions form the uniform triangular lattice. Their ground states are different according to the A site. Li2InMo3O8 undergoes conventional 120° long-range magnetic order below TN = 12 K whereas isomorphic Li2ScMo3O8 exhibits no long-range magnetic order down to 0.5 K. Here, we report exotic magnetisms in Li2InMo3O8 and Li2ScMo3O8 investigated by muon spin rotation (μSR) and inelastic neutron scattering (INS) spectroscopies using polycrystalline samples. Li2InMo3O8 and Li2ScMo3O8 show completely different behaviors observed in both μSR and INS measurements, representing their different ground states. Li2InMo3O8 exhibits spin wave excitation which is quantitatively described by the nearest neighbor anisotropic Heisenberg model based on the 120° spin structure. In contrast, Li2ScMo3O8 undergoes short-range magnetic order below 4 K with quantum-spin-liquid-like magnetic fluctuations down to the base temperature. Origin of the different ground states is discussed in terms of anisotropies of crystal structures and magnetic interactions.
Similar content being viewed by others
Introduction
When quantum spins are aligned on geometrically frustrated lattices, unusual ground state eventually emerges among energetically competed states1,2,3. Two-dimensional (2D) spin-1/2 triangular lattice Heisenberg antiferromagnet (TLHAF) is a prototypical system of geometrically frustrated magnets. Theoretically, the ground states of 2D TLHAF with both quantum and classical spins are known to be so-called 120° long-range order4,5,6,7. When perturbations such as the second nearest-neighbor interaction8, ring exchange interaction9, spatially anisotropic interactions10, and randomness of the strength of the nearest-neighbor interaction11 are set in, the system undergoes a quantum spin liquid (QSL) ground state where the system does not show static long-range magnetic order but shows long-range entanglement and fractional excitations1,2. Extensive experimental studies have also been conducted on spin-1/2 TLHAFs; the 120° long-range magnetic order is reported in Ba3CoSb2O912,13,14 whereas QSL state is proposed for the ground states of κ-(BEDT-TTF)2Cu2(CN)315,16, EtMe3Sb[Pd(dmit)2]217,18, YbMgGaO419,20,21,22 and 1T-TaS223. Furthermore, spin-1 TLHAF Ba3NiSb2O9 also shows QSL behaviors24,25,26. QSL with spinon Fermi surface27,28 was proposed and succeeded in understanding the QSL behaviors in such compounds20,21,26. However, experimental realization of the QSL ground state in spin-1/2 TLHAF systems is still limited and remains an intriguing pursuit.
Recently, cluster magnet LiZn2Mo3O8 has attracted considerable research interest as spin-1/2 TLHAF29. Seven 4d electrons in a Mo3O13 cluster occupy their orbitals, resulting in one unpaired electron. Unpaired electron with spin S = 1/2 remains in the total symmetry of the Mo3O13 cluster (A1 irreducible representation) with equal contributions from all three Mo atoms, and network of the magnetic clusters forms a uniform triangular lattice in LiZn2Mo3O8. The dominant magnetic interaction between spin-1/2 Mo3O13 clusters is antiferromagnetic29, yielding geometrical frustration. LiZn2Mo3O8 is therefore an ideal 2D spin-1/2 TLHAF system. Magnetic susceptibility and heat capacity measurements suggested that 2/3 of S = 1/2 spins are quenched below 96 K, and condensed valence bond state (VBS) where resonance valence-bond states30,31 coexist with remnant paramagnetic spins is proposed for the possible ground state29,32. Gapless spin excitations were reported by electron spin resonance32, 7Li nuclear magnetic resonance (NMR)32, muon spin rotation (μSR)32, and inelastic neutron scattering (INS)33 measurements. Emergent honeycomb lattice is theoretically proposed for the origin of the condensed VBS34. Recently, a 1/6-filled extended Hubbard model in an anisotropic kagome lattice is also proposed to account for the low temperature phase of LiZn2Mo3O835. However, intersite disorder between Li+ and Zn2+ ions is reported29,32, which may affect on the intrinsic magnetism in LiZn2Mo3O8.
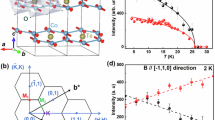
New molecular based triangular lattice systems Li2AMo3O8 where A = In or Sc are of particular interest in this context36,37. Li2AMo3O8 crystallizes in a hexagonal structure P63mc, and no intersite disorder between Li+ and A3+ sites exists (see Supplementary Information). As in LiZn2Mo3O8, spin-1/2 carrying Mo3O13 clusters are arranged on the structurally perfect triangular lattice separated by nonmagnetic Li and A layers in both compounds as shown in Fig. 1(a,b). Susceptibility measurements of both compounds report that the dominant magnetic interactions are antiferromagnetic and the effective moments are 1.61 μB (In) and 1.65 μB (Sc), which are close to peff = 1.73 μB the ideal value for spin S = 1/2. Spin-1/2 TLHAF is therefore realized in Li2AMo3O8, whose ground states are however different from each other. In Li2InMo3O8, long-range magnetic order develops below TN = 12 K with Curie-Weiss temperature of ΘCW = −242 K, and 7Li NMR study suggests that the magnetic structure is the 120° structure as described in Fig. 1(c). On the other hand, isostructural Li2ScMo3O8 shows no long-range magnetic order down to 0.5 K in spite of large Weiss temperature of ΘCW = −127 K. Instead, both magnetic susceptibility and heat capacity measurements indicate the development of short-range magnetic order below 10 K. Spin glass state is ruled out as the ground state of Li2ScMo3O8 since the magnetic susceptibility shows no splitting between zero-field-cooling and field-cooling processes37. Low-temperature heat capacity measurements in Li2ScMo3O8 shows sizable T-linear term γmag = 35.7 mJ/mol · K2, which is similar to those of QSL candidates κ-(BEDT-TTF)2Cu2(CN)316, EtMe3Sb[Pd(dmit)2]218, and Ba3CuSb2O938. Furthermore, different magnetic entropies between Li2ScMo3O8 and LiZn2Mo3O8 suggests that the ground state in Li2ScMo3O8 is QSL rather than condensed VBS. Because of easy access to two different ground states of spin-1/2 TLHAF, Li2AMo3O8 is an intriguing system to investigate 2D spin-1/2 TLHAF. However, lack of microscopic measurements prevents us from fully understanding the ground states and dynamics of Li2AMo3O8. In this paper, we investigate quantum magnetisms of polycrystalline Li2InMo3O8 and Li2ScMo3O8 by combination of μSR and time-of-flight (TOF) neutron scattering techniques.
Results and Discussion
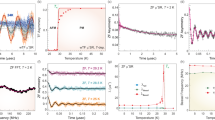
Zero field- (ZF-) μSR time spectra of Li2InMo3O8 at several temperatures are shown in Fig. 2(a). The spectra show a damping at around 12 K, and spectral oscillations appear at lower temperatures. It is a direct evidence of the long-range magnetic order as reported in the earlier studies36,37,39,40. Fourier transform of the spectrum at 3.33 K [see the inset of Fig. 2(a)] suggests that at least three different local fields are found in Li2InMo3O8, which is probably due to crystallographically inequivalent muon stopping sites indicated by our density functional theory (DFT) calculation (see Supplementary Fig. S3 for Li2ScMo3O8). The ZF-μSR spectra of Li2InMo3O8 are fitted by three cosine functions with transverse and longitudinal relaxations
where An and ABG are the positron decay asymmetries of each oscillation (n = 1~3) and background (mainly from a silver backing plate) components, fn is the precession frequency, ϕ is the initial phase, and λt (λl) is the transverse (longitudinal) relaxation rate. Fitting result at each temperature is shown in Fig. 2(a). Local magnetic fields of 84.9(3), 103.1(2), and 151.5(5) G are extracted at 3.33 K, and these values are comparable in magnitude of local fields that are observed in spin-1/2 magnets41. Figure 2(c) shows temperature dependences of f1, f2, and f3, representing that long-range magnetic order evolves in Li2InMo3O8 below TN = 12 K with the critical exponents β ~ 0.33.
ZF- and LF-μSR results on Li2AMo3O8. μSR time spectra of (a) Li2InMo3O8 and (b) Li2ScMo3O8. Solid lines in each panel represent the fitting curves (see the main text). A Fourier transform of the μSR time spectrum of Li2InMo3O8 at 3.33 K (real amplitude) is plotted in the inset of (a). The inset of (b) shows a magnified view of the spectrum of Li2ScMo3O8 at 0.07 K under HLF = 1 kG. (c) Temperature dependences of local fields in Li2InMo3O8 and Li2ScMo3O8. (d) Temperature dependences of muon relaxation rates λf (left scale) and λs (right scale) of Li2ScMo3O8 under longitudinal field. Solid line is calculated λ (right scale) using Eq. (7).
In the meanwhile, ZF-μSR time spectrum of Li2ScMo3O8 at 0.07 K shows a highly damped oscillation with a pronounced reduction of the 1/3 tail as described in Fig. 2(b). To see the temperature evolution of the local fields in Li2ScMo3O8, the ZF-μSR spectrum are fitted by combination of transverse and longitudinal relaxations
The fitting result at each temperature is plotted in Fig. 2(b), and temperature dependence of the local field fSc is also plotted in Fig. 2(c). One can clearly see the temperature evolution of fSc below 4 K with the critical exponent β ~ 0.28 which is similar to those of Li2InMo3O8. Therefore, magnetic nature of these compounds are essentially the same, but it should be noted that the ground state of Li2ScMo3O8 is short-range magnetic order by considering the strong damping of the oscillation below 4 K. The anomaly at 4 K was also found in the temperature derivative of the magnetic susceptibility37. Although the short-range magnetic order develops in Li2ScMo3O8 below 4 K, the spectrum shows a moderate tail over a long period of time, suggesting that spin fluctuation survives even at 0.07 K. To explicitly distinguish the spin fluctuation of the Mo3O13 cluster, we performed longitudinal field- (LF-) μSR measurements on Li2ScMo3O8 under longitudinal magnetic field (HLF) of 1 kG. Figure 2(b) and its inset display a LF-μSR time spectrum measured at 0.07 K. HLF = 1 kG seems to be sufficient to quench (decouple) muon spin relaxations by both nuclear dipoles and the short-range ordered state. The characteristic LF-μSR spectrum of Li2ScMo3O8 at 0.07 K was fitted by the following equation
where Af and As are asymmetries of fast (λf) and slow (λs) relaxation components, respectively (Af + As = 0.16), and ABG is the background asymmetry (ABG = 0.03). The fitting results are described by the solid lines in Fig. 2(b) and its inset. We also fit LF-μSR time spectra under HLF = 1 kG at several temperatures, and obtained temperature dependences of λf and λs are plotted in Fig. 2(d). λf shows a rapid relaxation with relative signal amplitude of ~3%. It mainly corresponds to the remnant signal from the short-range ordered state since λf exhibits a steep increase at 4 K as temperature goes down. On the other hand, λs shows a slow relaxation with two orders of magnitude less than λf, which is related to the intrinsic spin fluctuation of the Mo3O13 cluster. Remarkably, temperature dependence of λs shows a temperature-independent plateau below 1 K and converges into the finite value of ~0.002 μs−1 which is very close to that of triangular lattice QSL 1T-TaS2 (λ = 0.0023 μs−1 at 0.07 K)23. Indeed, such low-temperature plateau behaviors of muon relaxation rate is common feature in the TLHAF QSL candidates20,25, which will be discussed again. To obtain complementary information to our μSR results on Li2AMo3O8, TOF neutron scattering measurements were also conducted.
Elastic neutron scattering spectra of Li2InMo3O8 below and above TN are shown in Fig. 3(e). A magnetic Bragg peak appears at momentum transfer Q = 0.719(1) Å−1 below TN. The Q position corresponds to (1/3, 1/3, 0), indicating the 120° magnetic structure consistent with the previous 7Li-NMR measurements37. By comparing the intensity of the magnetic peak with those of nuclear Bragg peaks, the ordered moment at 4.6 K is estimated to be 0.51(3) μB. Theoretically, the magnetic moment is reduced by about 59% for the spin-1/2 TLHAF6, which is close to the observed ordered moment (reduced by 49% assuming g = 2). The reduced moment originates in a combination of geometrical frustration and quantum fluctuation. Neutron scattering intensity (I) map from Li2InMo3O8 as a function of Q and energy transfer (\(\hslash \omega \)) at 4.5 K (<TN) is shown in Fig. 3(a). Dispersive excitation centered at the magnetic zone center (1/3, 1/3, 0) was observed. Because of the Q position, the excitation is assigned to be the spin wave excitation in the long-range magnetic ordered state. Energy spectrum at the magnetic zone center exhibits a substantial peak at \(\hslash \omega =2.08(3)\) meV as shown in Fig. 3(f). This result claims that one branch (or some branches) of the spin wave excitation has spin gap at the magnetic zone center due to the magnetic anisotropy. On the other hand, magnetic signals at the magnetic zone center become quasielastic above TN as shown in Fig. 3(b,f). Therefore, the gap-like excitation is a characteristic feature of the long-range magnetic ordered state. To observe the whole structure of the spin wave excitation at 4.5 K, \(I(Q,\hslash \omega )\) map using higher Ei is presented in Fig. 3(c). The spin wave excitation survives up to ~9 meV. Q dependences of the spin wave intensities at various \(\hslash \omega \)s are plotted in Fig. 3(g). The spectra are asymmetric at \(\hslash \omega > 3.0\) meV, and the peak shifts to lower Q at higher \(\hslash \omega \). This result suggests that the squared magnetic form factor (|F(Q)|2) of the Mo3O13 cluster decreases quickly and is negligible at high Q, representing the unpaired electron with equal contributions from all three Mo atoms in Li2InMo3O8.
TOF neutron scattering results on Li2InMo3O8. Low-energy inelastic neutron scattering intensity maps at (a) 4.6 K and (b) 13.5 K measured with Ei = 11.9 meV. (c) High-energy inelastic neutron scattering intensity map at 4.6 K measured with Ei = 22.0 meV. (d) Calculated inelastic neutron scattering intensity map at 4.6 K using the optimum parameters as described in the main text. Calculated energy resolution for Ei = 11.9 meV was convoluted. (e) Elastic neutron scattering intensities at 4.6 and 18.7 K with energy window of [−0.15, 0.15] meV. Solid lines represent the fitting result using the Gaussian function with linear background. (f) Energy spectra integrated over Q = [0.69, 0.77] Å−1 at 4.6 and 13.5 K measured with Ei = 11.9 meV. (g) Q dependences of the neutron scattering intensities at several energy windows. Each energy window was [1.5, 2.0], [2.0, 2.5], [2.5, 3.0], [3.0, 3.5], and [3.5, 4.0] meV with Ei = 11.9 meV (red), [4.0, 4.5] and [4.5, 5.0] meV with Ei = 15.8 meV (blue), [5.0, 6.0] and [6.0, 7.0] meV with Ei = 22.0 meV (green), and [7.0, 8.0] meV with Ei = 32.7 meV (black), respectively. Constant background was subtracted from each Q dependence. Solid lines are calculated results using the optimum parameters in Eq. (5).
For quantitative analysis on the spin wave excitation in Li2InMo3O8, semi-classical linear spin wave (LSW) analysis was performed considering the 120° spin structure on the spin-1/2 2D Mo3O13-based triangular lattice [Fig. 1(c)]. The gap-like excitation at the magnetic zone center in the long-range magnetic ordered state is also observed in the other spin-1/2 triangular lattice system Ba3CoSb2O913, and the peak energy (E0) roughly scales with TN in these compounds: E0 = 0.65 meV and TN = 3.8 K in Ba3CoSb2O913 whereas E0 = 2.08 meV and TN = 12 K in Li2InMo3O8. This suggests that the origin of the gap-like excitation in Li2InMo3O8 is the same as that in Ba3CoSb2O913. Therefore, as in Ba3CoSb2O912,13,14, the nearest-neighbor anisotropic exchange interaction was considered as the model Hamiltonian for Li2InMo3O8
where α, J, and δ represent the renormalization factor, the nearest neighbor exchange coupling constant, and the anisotropic factor. J was fixed to 112 K determined by the magnetic susceptibility measurement37. By fitting the calculated powder-averaged Q dependences to the experimental results at different \(\hslash \omega \)s (2~7.5 meV) simultaneously, optimum parameters were yielded
Fitting results together with the experimental results are shown in Fig. 3(g), and calculated LSW \(I(Q,\hslash \omega )\) map is also shown in Fig. 3(d). Satisfactory agreements with calculation and experiment were confirmed. Obtained α is smaller than 1, indicating a negative quantum renormalization effect theoretically proposed for 2D spin-1/2 TLHAF42,43,44. Similar negative quantum renormalization effect (α ~ 0.65) was also reported in Ba3CoSb2O914. Therefore, observed magnetic excitations of Li2InMo3O8 in the accessible \((Q,\hslash \omega )\) region are well understood by the semi-classical LSW theory assuming the 120° magnetic structure on the spin-1/2 Mo3O13 triangular lattice.
In contrast to Li2InMo3O8, no magnetic Bragg peak evolves in the elastic channel down to 0.3 K in Li2ScMo3O8 as plotted in Fig. 4(c), in agreement with our μSR results. On the other hand, diffuse scattering expected for the short-range order is not observed in our neutron measurements. Strong incoherent scattering may smear out such magnetic diffuse scattering in Li2ScMo3O8. Figure 4(a) depicts \(I(Q,\hslash \omega )\) map at 0.3 K. Clear diffuse scattering was observed in the inelastic channel. Although both magnetic excitations in Li2InMo3O8 and Li2ScMo3O8 are centered at Q ~ 0.7 Å−1 [Figs 3(a) and 4(a)], the overall structures are different, representing their different ground states. In Li2ScMo3O8, steep continuum excitation was observed. The Q dependences of the magnetic excitations are invariant in the different energy windows as shown in Fig. 4(d). Steep continuum excitation, or spinon continuum, is the common feature of the magnetic excitations in the QSL candidates3,21,22,26,45. \(I(Q,\hslash \omega )\) map at high temperature (22 K) is also shown in Fig. 4(b). Although overall magnetic fluctuation at 22 K is similar to that at 0.3 K, there are some differences. Scattering intensity decreases at 22 K. In addition, as shown in Fig. 4(e), spectrum weight of the Q dependence at 2 meV slightly shifts to Q = 0 at high temperature, which is also observed in other QSL candidates22,26,45.
TOF neutron scattering results on Li2ScMo3O8. Inelastic neutron scattering intensity maps with Ei = 10.3 meV measured at (a) 0.3 K and (b) 22 K. (c) Elastic neutron scattering intensities with energy window of [−0.075, 0.075] meV at 0.3 and 22 K with Ei = 10.3 meV. (d) Q dependences of the neutron scattering intensities at several energy windows at 1.7 K. Each energy window was [1.5, 2.5] meV with Ei = 7.5 meV, [2.5, 3.5] meV with Ei = 10.3 meV, [3.5, 4.5] meV with Ei = 15.0 meV, and [4.5, 5.5] meV with Ei = 23.9 meV, respectively. (e) Q dependences of the neutron scattering intensities with [1.5, 2.5] meV at 0.3 and 22 K using Ei = 7.5 meV. (f) Dynamical spin susceptibilities at Q = [0.6, 0.8] Å−1 for 0.3, 10, 22, and 40 K. Solid lines are the fitting results by the quasielastic Lorentzian as described in the main text. (g) Temperature dependences of static spin susceptibility χ′ (left scale) and relaxation rate Γ (right scale) obtained by the fitting in panel (f). Solid line is a scaled bulk magnetic susceptibility (χbulk = M/H) measured with H = 1 T.
To investigate in more detail the characteristic energy (or time) scale of the steep continuum in Li2ScMo3O8, the dynamical spin susceptibilities \(\chi ^{\prime\prime} (\hslash \omega )=[1-\exp (\,-\,\hslash \omega /{k}_{B}T)]/|F(Q){|}^{2}I(\hslash \omega )\) at Q = [0.6, 0.8] Å−1 where the magnetic signal is maximal are plotted for different temperatures in Fig. 4(f). The spectra are well fitted by the quasielastic Lorentzian \(\chi ^{\prime\prime} (\hslash \omega )=\chi ^{\prime} \hslash \omega {\rm{\Gamma }}/[{(\hslash \omega )}^{2}+{{\rm{\Gamma }}}^{2}]\) where χ′ is the static susceptibility and Γ the spin relaxation rate [or peak position of \(\chi ^{\prime\prime} (\hslash \omega )\)]. The temperature dependences of the resulting parameters are shown in Fig. 4(g). Upon decreasing temperature, Γ decreases while χ′ increases. Contrary to the conventional long-range ordered magnets, no divergent behavior was observed in the temperature dependences of χ′ and Γ. It should be noted that χ′ scales with bulk magnetic susceptibility χbulk over the temperature range of 3 ≤ T ≤ 40 K [see solid line in Fig. 4(g)] and Γ is also scaled by the muon relaxation rate λs as discussed below. These fittings also extract two important features of the steep continuum in Li2ScMo3O8: (1) the magnetic excitation is gapless consistent with the heat capacity measurement37 and (2) the dynamical spin susceptibility extends from the elastic channel up to at least 9.5 meV which is about 1.6 J where J (=67 K) is determined by the magnetic susceptibility measurement37.
Complementary analysis of μSR and INS results enables us to exclusively clarify the quantum fluctuations in Li2ScMo3O8. Muon spin relaxation rate λs in Fig. 2(d) is related to the spin relaxation rate of the magnetic fluctuation Γ in Fig. 4(g) on the basis of following Redfield’s formula46
where γμ and δμ are the gyromagnetic ratio of muon (=2π × 135.54 MHz/T) and average distribution of local magnetic fields at muon sites. We performed electrostatic potential calculations using a point-charge model47 and estimated δμ = 204.8 G for Li2ScMo3O8 (see Supplementary Information). Since HLF (=1 kG = 8.5 × 108 Hz) is much smaller than Γ (=2.7 meV = 6.5 × 1011 Hz at 0.3 K) in Li2ScMo3O8, Eq. (6) is reformulated as
We plotted calculated temperature dependence of λ using Γ obtained by our INS measurements and compared with λs obtained by our LF-μSR measurements [see solid line for calculation and circles for μSR results in Fig. 2(d)]. Quantitative agreement can be seen; the anomaly around 4 K is artificial feature owing to λf. Therefore, both μSR and INS measurements exhibit that quantum fluctuations persist at the lowest measured temperature. As mentioned above, such low-temperature plateaus of the relaxation rates were widely observed in the triangular-lattice20,25 and kagome-lattice45,48,49,50,51 QSL candidates.
To account for the QSL-like excitations in Li2ScMo3O8, we now consider the spinon Fermi surface QSL model. In Li2ScMo3O8, no static long-range order was detected even down to 0.07 K [Figs 2(b) and 4(c)]. Alternatively, gapless continuum in Li2ScMo3O8 was observed at Q = 0.726(4) Å−1 corresponding to the (1/3, 1/3, 0) position [Fig. 4(a,d,f)]. Moreover, both λs and Γ exhibit temperature-independent plateaus at low temperature [Figs 2(d) and 4(g)]. These features are well explained by QSL with spinon Fermi surface27,28. As discussed in earlier works20,21,26, the spinon Fermi surface QSL model on the spin-1/2 TLHAF expects that (1) absence of static long-range magnetic order, (2) muon spin relaxation rate approach a finite value as temperature approaches zero, (3) magnetic excitation is gapless continuum, and (4) \(\chi ^{\prime\prime} (Q,\hslash \omega )\) shows the maximum intensity at the corner of the 2D Brillouin zone [e.g. (1/3, 1/3, 0)]. All observed features of the magnetic fluctuation in Li2ScMo3O8 can be well described by the spinon Fermi surface QSL model. Although the second peak of the spinon continuum in Ba3NiSb2O9 was also observed at (2/3, 2/3, 0)26, the second peak in Li2ScMo3O8 was not detected at (2/3, 2/3, 0) corresponding to Q = 1.45 Å−1 as shown in Fig. 4(d) because of the quick decay of the squared magnetic form factor of the Mo3O13 cluster33. By performing complementary analysis on μSR and INS results, we conclude that Li2ScMo3O8 undergoes the short-range magnetic order below 4 K with the QSL-like fluctuations which persist down to the lowest temperature.
We compare the Mo3O13-cluster-based triangular lattice antiferromagnets, Li2AMo3O8 and LiZn2Mo3O8, in line with the recent theory by Chen et al.35. They proposed a 1/6-filled Hubbard model on an anisotropic kagome lattice with the nearest-neighbor electron hopping and repulsions35 to account for the magnetism in LiZn2Mo3O829. Electron is fractionalized into charged boson and spin-carring spinons; plaquette charge order emerges as the charge ground state and the spin degree of freedom can be then described by U(1) QSL with spinon Fermi surface, which can explain the unusual magnetic susceptibility in LiZn2Mo3O829. For comparison with different compounds, they introduce a phenomenological parameter ξ to characterize the anisotropy of the Mo kagome lattice: ξ = dinter/dintra where dintra (dinter) is the intracluster (intercluster) Mo-Mo bond length. Large anisotropy ξ tends to suppress charge fluctuations between clusters leading to the 120° long-range magnetic order whereas small anisotropy ξ corresponds to large charge fluctuation generating the U(1) QSL with spinon Fermi surface. Using the structural parameters summarized in Supplementary Information, we estimated ξ as 1.271, 1.269, and 1.258 for Li2InMo3O8, Li2ScMo3O8, and LiZn2Mo3O829, respectively. The phenomenological parameter ξ explains the different ground states between the 120° long-range magnetic order in Li2InMo3O8 and the condensed VBS in LiZn2Mo3O8. However, the ξ values of Li2InMo3O8 and Li2ScMo3O8 are very close to each other in spite of their different ground states. Nevertheless, 115In and 45Sc NMR measurements on Li2AMo3O8 reported that charge fluctuation in Li2ScMo3O8 is 2.6 times larger than that in Li2InMo3O852, and the difference between charge fluctuations can qualitatively explain the different ground states of Li2InMo3O8 and Li2ScMo3O8. Therefore, the anisotropic parameter for the Mo kagome lattice, ξ, is too simplified to explain the different ground states in Li2AMo3O8, and more detailed parameter is required for Li2AMo3O8.
We also compare the magnetic excitations in Li2InMo3O8 and Li2ScMo3O8 to discuss the origin of the different ground states. Although both magnetic excitations in Li2InMo3O8 and Li2ScMo3O8 center at Q ~ 0.72 Å−1, low-energy magnetic excitations show opposite behaviors. The magnetic excitation at the magnetic zone center in Li2InMo3O8 clearly exhibits the peak at 2.08(3) meV [Fig. 3(a,f)]. Our LSW analysis suggests that the anisotropic exchange interaction is necessary to reproduce the peak. Meanwhile, the gapless magnetic excitation in Li2ScMo3O8 indicates that magnetic anisotropy is negligibly small in Li2ScMo3O8 [Fig. 4(a,f)]. Thus, the difference in the magnetic anisotropy is another possibility of the origin of the different ground states in Li2AMo3O8. In fact, the gap-like excitation was observed in the long-range ordered state of Ba3CoSb2O913,14, whereas the gapless magnetic excitations in the QSL systems YbMgGaO421,22 and Ba3NiSb2O926. INS measurements on magnetic excitations in the substitution system Li2(In1−xScx)Mo3O840 are effective to further elucidate the origin of different magnetic ground states, which is left for future work.
Conclusion
We performed a comprehensive study on the quantum magnetisms in the Mo3O13-cluster-based spin-1/2 triangular lattice antiferromagnets, Li2InMo3O8 and Li2ScMo3O8 by means of μSR and TOF neutron scattering techniques. Spin wave excitation in Li2InMo3O8 was well described by the nearest neighbor anisotropic Heisenberg model based on the 120° spin structure. Li2ScMo3O8 exhibits the short-range magnetic order below 4 K with the QSL-like fluctuations which persist down to the lowest temperature. The origin of the different magnetic ground states in Li2AMo3O8 is discussed in terms of anisotropies of crystal structures and magnetic interactions.
Methods
The preparation of polycrystalline Li2InMo308 (Li2ScMo3O8) was carried out by two steps37. First, to synthesize a precursor Li2MoO4, a mixture with a ratio of MoO3:Li2CO3 = 1:1 was ground, placed in an alumina crucible, and heated at 873 K for 24 hours in air; we repeated this step for three times. Then, a mixture having a ratio of In2O3 (Sc2O3):Li2MoO4:MoO3:Mo = 0.5:1:0.84:1.16 was ground, pressed into a pellet, sealed in an evacuated quartz tube, heated at 923 K for 12 hours, and heated at 1198 K (1173 K) for 24 hours; we repeated this step for two times. Magnetization measurements were performed using a commercial superconducting quantum interference device (SQUID) magnetometer (Quantum Design Magnetic Property Measurement System, MPMS). ZF- and LF-μSR experiments were performed using the Advanced Research Targeted Experimental Muon Instrument at the S1 line spectrometer (ARTEMIS)53 with a conventional 4He flow cryostat and the D1 spectrometer53 with a 3He-4He dilution refrigerator installed at Materials and Life Science Experimental Facility (MLF), Japan Proton Accelerator Research Complex (J-PARC). We used the VASP software54 for DFT calculation and the DipElec program47 to calculate the local magnetic fields in Li2ScMo3O8. TOF neutron scattering measurements were performed using the Fermi chopper spectrometer 4SEASONS at MLF, J-PARC55. Frequencies of the Fermi chopper were 350 and 250 Hz for the In and Sc systems, resulting in the combinations of incident neutron energies of 11.9, 15.8, 22.0, and 32.7 meV, and 7.5, 10.3, 15.0, and 23.9 meV56, respectively. A standard top-loading cryostat at 4SEASONS was used for the measurements on Li2InMo3O8, whereas a 4He refrigerator and a 3He cryostat were used for Li2ScMo3O8. Empty can was measured at corresponding temperatures, and then subtracted from raw data of Li2ScMo3O8. TOF data were visualized by software suite Utsusemi57. Neutron scattering intensities are converted to the absolute unit using the incoherent scattering of each sample58 after correction of the neutron absorption effect. Squared magnetic form factor of the Mo3O13 cluster33 and \(\hslash \omega \)-dependent energy resolution at 4SEASONS59 were included in the LSW calculations for Li2InMo3O8.
Data Availability
The datasets generated and analyzed during the current study are available from the corresponding author.
References
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Savary, L. & Balents, L. Quantum spin liquids: a review. Rep. Prog. Phys. 80, 016502 (2017).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Seabra, L., Momoi, T., Sindzingre, P. & Shannon, N. Phase diagram of the classical Heisenberg antiferromagnet on a triangular lattice in an applied magnetic field. Phys. Rev. B 84, 214418 (2011).
Huse, D. A. & Elser, V. Simple variational wave functions for two-dimensional Heisenberg spin-1/2 antiferromagnets. Phys. Rev. Lett. 60, 2531–2534 (1988).
Capriotti, L., Trumper, A. E. & Sorella, S. Long-range Néel order in triangular Heisenberg model. Phys. Rev. Lett. 82, 3899–3902 (1999).
White, S. R. & Chernyshev, A. L. Néel order in square and triangular lattice Heisenberg models. Phys. Rev. Lett. 99, 127004 (2007).
Iqbal, Y., Hu, W.-J., Thomale, R., Poilblanc, D. & Becca, F. Spin liquid nature in the Heisenberg J 1–J 2 triangular antiferromagnet. Phys. Rev. B 93, 144411 (2016).
Motrunich, O. I. Variational study of triangular spin-1/2 model with ring exchanges and spin liquid state in κ-(ET)2Cu2(CN)3. Phys. Rev. B 72, 045105 (2005).
Trumper, A. E. Spin-wave analysis to the spatially anisotropic Heisenberg antiferromagnet on a triangular lattice. Phys. Rev. B 72, 2987–2989 (1999).
Watanabe, K., Kawamura, H., Nakano, H. & Sakai, T. Quantum spin-liquid behavior in the spin-1/2 random Heisenberg antiferromagnet on the triangular lattice. J. Phys. Soc. Jpn. 83, 034714 (2014).
Shirata, Y., Tanaka, H., Matsuo, A. & Kindo, K. Experimental realization of a spin-1/2 triangular-lattice Heisenberg antiferromagnet. Phys. Rev. Lett. 108, 057205 (2012).
Ma, J. et al. Static and dynamical properties of the spin-1/2 equilateral triangular-lattice antiferromagnet Ba3CoSb2O9. Phys. Rev. Lett. 116, 087201 (2016).
Ito, S. et al. Structure of the magnetic excitations in the spin-1/2 triangular-lattice Heisenberg antiferromagnet Ba3CoSb2O9. Nat. Commun. 8, 235 (2017).
Shimizu, Y., Miyagawa, K., Kanoda, K., Maesato, M. & Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003).
Yamashita, S. et al. Thermodynamic properties of a spin-1/2 spin-liquid state in a κ-type organic salt. Nat. Phys. 4, 459–462 (2008).
Yamashita, M. et al. Highly mobile gapless excitations in a two-dimensional candidate quantum spin liquid. Science 328, 1246–1248 (2010).
Yamashita, S., Yamamoto, T., Nakazawa, Y., Tamura, M. & Kato, R. Gapless spin liquid of an organic triangular compound evidenced by thermodynamic measurements. Nat. Commun. 2, 275 (2011).
Li, Y. et al. Gapless quantum spin liquid ground state in the two-dimensional spin-1/2 triangular antiferromagnet YbMgGaO4. Sci. Rep. 5, 16419 (2015).
Li, Y. et al. Muon spin relaxation evidence for the U(1) quantum spin-liquid ground state in the triangular antiferromagnet YbMgGaO4. Phys. Rev. Lett. 117, 097201 (2016).
Shen, Y. et al. Evidence for a spinon Fermi surface in a triangular-lattice quantum-spin-liquid candidate. Nature 540, 559–562 (2016).
Paddison, J. A. M. et al. Continuous excitations of the triangular-lattice quantum spin liquid YbMgGaO4. Nat. Phys. 13, 117–122 (2017).
Klanjšek, M. et al. A high-temperature quantum spin liquid with polaron spins. Nat. Phys. 13, 1130–1134 (2017).
Cheng, J. G. et al. High-pressure sequence of Ba3NiSb2O9 structural phases: new S = 1 quantum spin liquids based on Ni2+. Phys. Rev. Lett. 107, 197204 (2011).
Quilliam, J. A. et al. Gapless quantum spin liquid ground state in the spin-1 antiferromagnet 6HB-Ba3NiSb2O9. Phys. Rev. B 93, 214432 (2016).
Fåk, B. et al. Evidence for a spinon Fermi surface in the triangular S = 1 quantum spin liquid Ba3NiSb2O9. Phys. Rev. B 95, 060402(R) (2017).
Lee, S.-S. & Lee, P. A. U(1) gauge theory of the Hubbard model: spin liquid states and possible application to κ-(BEDT-TTF)2Cu2(CN)3. Phys. Rev. Lett. 95, 036403 (2005).
Norman, M. R. & Micklitz, T. How to measure a spinon Fermi surface. Phys. Rev. Lett. 102, 067204 (2009).
Sheckelton, J. P., Neilson, J. R., Soltan, D. G. & McQueen, T. M. Possible valence-bond condensation in the frustrated cluster magnet LiZn2Mo3O8. Nat. Mater. 11, 493–496 (2012).
Anderson, P. W. Resonating valence bonds: a new kind of insulator? Mater. Res. Bull. 8, 153–160 (1973).
Fazekas, P. & Anderson, P. W. On the ground state properties of the anisotropic triangular antiferromagnet. Phil. Mag. 30, 423–440 (1973).
Sheckelton, J. P. et al. Local magnetism and spin correlations in the geometrically frustrated cluster magnet LiZn2Mo3O8. Phys. Rev. B 89, 064407 (2014).
Mourigal, M. et al. Molecular quantum magnetism in LiZn2Mo3O8. Phys. Rev. Lett. 112, 027202 (2014).
Flint, R. & Lee, P. A. Emergent honeycomb lattice in LiZn2Mo3O8. Phys. Rev. Lett. 111, 217201 (2013).
Chen, G., Kee, H.-Y. & Kim, Y. B. Cluster Mott insulators and two Curie-Weiss regimes on an anisotropic kagome lattice. Phys. Rev. B 93, 245134 (2016).
Gall, P., Orabi, R. A. R. A., Guizouarn, T. & Gougeon, P. Synthesis, crystal structure and magnetic properties of Li2InMo3O8: a novel reduced molybdenum oxide containing magnetic Mo3 clusters. J. Solid State Chem. 208, 99 (2013).
Haraguchi, Y., Michioka, C., Imai, M., Ueda, H. & Yoshimura, K. Spin-liquid behavior in the spin-frustrated Mo3 cluster magnet Li2ScMo3O8 in contrast to magnetic ordering in isomorphic Li2InMo3O8. Phys. Rev. B 92, 014409 (2015).
Zhou, H. D. et al. Spin liquid state in the S = 1/2 triangular lattice Ba3CuSb2O9. Phys. Rev. Lett. 106, 147204 (2011).
Sugiyama, J. et al. Internal magnetic field on the two-dimensional triangular lattice formed by Mo3O8 trimers. J. Phys.: Conf. Ser. 21, 011012 (2018).
Akbari-Sharbaf, A. et al. Tunable quantum spin liquidity in the 1/6th-filled breathing kagome lattice. Phys. Rev. Lett. 120, 227201 (2018).
Portis, A. M. & Celio, M. Muon and other studies of magnetic ordering in cuprate layer-compounds. Hyperfine Interactions 49, 129–166 (1989).
Starykh, O. A., Chubukov, A. V. & Abanov, A. G. Flat spin-wave dispersion in a triangular antiferromagnet. Phys. Rev. B 74, 180403(R) (2006).
Zheng, W., Fjarestand, J. O., Singh, R. R. P., McKenzie, R. H. & Coldea, R. Excitation spectra of the spin-1/2 triangular-lattice Heisenberg antiferromagnet. Phys. Rev. B 74, 224420 (2006).
Chernyshev, A. L. & Zhitomirsky, M. E. Spin waves in a triangular lattice antiferromagnet: decays, spectrum renormalization, and singularities. Phys. Rev. B 79, 144416 (2009).
Fåk, B. et al. Kapellasite: a kagome quantum spin liquid with competing interactions. Phys. Rev. Lett. 109, 037208 (2012).
Slichter, C. P. Principles of Magnetic Resonance. 3rd edition, (Springer Verlag, New York, 1990).
Kojima, K. M. et al. Site-dilution in the quasi-one-dimensional antiferromagnet Sr2(Cu1−xPdx)O3: reduction of Néel temperature and spatial distribution of ordered moment sizes. Phys. Rev. B 70, 094402 (2004).
Mendels, P. et al. Quantum magnetism in the paratacamite family: towards an ideal kagomé lattice. Phys. Rev. Lett. 98, 077204 (2007).
Kermarrec, E. et al. Spin-liquid ground state in the frustrated kagome antiferromagnet MgCu3(OH)6Cl2. Phys. Rev. B 84, 100401(R) (2011).
Clark, L. et al. Gapless spin liquid ground state in the S = 1/2 vanadium oxyfluoride kagome antiferromagnet [NH4]2[C7H14N][V7O6F18]. Phys. Rev. Lett. 110, 207208 (2013).
Gomilsek, M. et al. Instabilities of spin-liquid states in a quantum kagome antiferromagnet. Phys. Rev. B 93, 060405(R) (2016).
Haraguchi, Y., Michioka, C., Ueda, H. & Yoshimura, K. Charge fluctuation in S = 1/2 triangular lattice cluster antiferromagnets Li2ScMo3O8 and Li2InMo3O8. J. Phys.: Conf. Series 868, 012022 (2017).
Kojima, K. M. et al. New μSR spectrometer at J-PARC MUSE based on Kalliope detectors. J. Phys. Conf. Ser. 551, 012063 (2014).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kajimoto, R. et al. The Fermi chopper spectrometer 4SEASONS at J-PARC. J. Phys. Soc. Jpn. 80, SB025 (2011).
Nakamura, M. et al. First demonstration of novel method for inelastic neutron scattering measurement utilizing multiple incident energies. J. Phys. Soc. Jpn. 78, 093002 (2009).
Inamura, Y., Nakatani, T., Suzuki, J. & Otomo, T. Development status of software “Utsusemi” for chopper spectrometers at MLF, J-PARC. J. Phys. Soc. Jpn. 82, SA031 (2013).
Xu, G., Xu, Z. & Tranquada, J. M. Absolute cross-section normalization of magnetic neutron scattering data. Rev. Sci. Instrum. 84, 083906 (2013).
Iida, K. et al. Energy- and Q-resolution investigations of a chopper spectrometer 4SEASONS at J-PARC. JPS Conf. Proc. 1, 014016 (2014).
Acknowledgements
We thank Seiko Ohira-Kawamura and Kim Sandvik for helpful discussion and Hua Li for DFT calculations. We also acknowledge technical supports from the MLF sample environment team. Magnetic susceptibility measurements were performed at the CROSS user laboratories. The synchrotron X-ray diffraction experiments were conducted at BL5S2 of Aichi Synchrotron Radiation Center, Aichi Science and Technology Foundation, Aichi, Japan (Proposal Nos. 201803046 and 201803047). The μSR measurements at the S1 and D1 beamlines were conducted under the user program with proposal number 2017B0033. The proposal numbers for the TOF neutron scattering experiments at 4SEASONS were 2016I0001, 2017A0004, 2017B0030, and 2018I0001. The DFT calculations were supported by the Condensed Matter Research Center, Institute of Materials Structure Science, KEK, and the KEK Large Scale Simulation Program (Nos 15/16-07 and 16/17-18). This work was partially supported by JSPS KAKENHI Grant Numbers JP17K14349 and JP18K03529, and the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (20181072).
Author information
Authors and Affiliations
Contributions
K.I. designed the project. H.Y. and Y. Ishii synthesized the polycrystalline samples. H.Y., Y. Ishii, M.I. and K.I. characterized the samples. N.K. conducted synchrotron X-ray diffraction measurements and Rietveld analysis. H.O., A.K., R. Kadono, K.I. and R. Kajimoto conducted muon experiments while K.I., R. Kajimoto, H.Y., Y. Inamura, N.M. and M.I. performed neutron scattering measurements. K.I., H.O. and N.K. analyzed the data and wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iida, K., Yoshida, H., Okabe, H. et al. Quantum magnetisms in uniform triangular lattices Li2AMo3O8 (A = In, Sc). Sci Rep 9, 1826 (2019). https://doi.org/10.1038/s41598-018-36123-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-36123-7
This article is cited by
-
Quantum spin liquid and cluster Mott insulator phases in the Mo3O8 magnets
npj Quantum Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.