Quantum magnetisms in uniform triangular lattices Li₂AMo₃O₈ (A = In, Sc)

Abstract

Molecular based spin-1/2 triangular lattice systems such as LiZn₂Mo₃O₈ have attracted research interest. Distortions, defects, and intersite disorder are suppressed in such molecular-based magnets, and intrinsic geometrical frustration gives rise to unconventional and unexpected ground states. Li₂AMo₃O₈ (A = In or Sc) is such a compound where spin-1/2 Mo₃O₁₃ clusters in place of Mo ions form the uniform triangular lattice. Their ground states are different according to the A site. Li₂InMo₃O₈ undergoes conventional 120° long-range magnetic order below T_N = 12 K whereas isomorphic Li₂ScMo₃O₈ exhibits no long-range magnetic order down to 0.5 K. Here, we report exotic magnetisms in Li₂InMo₃O₈ and Li₂ScMo₃O₈ investigated by muon spin rotation (μSR) and inelastic neutron scattering (INS) spectroscopies using polycrystalline samples. Li₂InMo₃O₈ and Li₂ScMo₃O₈ show completely different behaviors observed in both μSR and INS measurements, representing their different ground states. Li₂InMo₃O₈ exhibits spin wave excitation which is quantitatively described by the nearest neighbor anisotropic Heisenberg model based on the 120° spin structure. In contrast, Li₂ScMo₃O₈ undergoes short-range magnetic order below 4 K with quantum-spin-liquid-like magnetic fluctuations down to the base temperature. Origin of the different ground states is discussed in terms of anisotropies of crystal structures and magnetic interactions.

Introduction

When quantum spins are aligned on geometrically frustrated lattices, unusual ground state eventually emerges among energetically competed states^1,2,3. Two-dimensional (2D) spin-1/2 triangular lattice Heisenberg antiferromagnet (TLHAF) is a prototypical system of geometrically frustrated magnets. Theoretically, the ground states of 2D TLHAF with both quantum and classical spins are known to be so-called 120° long-range order^4,5,6,7. When perturbations such as the second nearest-neighbor interaction⁸, ring exchange interaction⁹, spatially anisotropic interactions¹⁰, and randomness of the strength of the nearest-neighbor interaction¹¹ are set in, the system undergoes a quantum spin liquid (QSL) ground state where the system does not show static long-range magnetic order but shows long-range entanglement and fractional excitations^1,2. Extensive experimental studies have also been conducted on spin-1/2 TLHAFs; the 120° long-range magnetic order is reported in Ba₃CoSb₂O₉^12,13,14 whereas QSL state is proposed for the ground states of κ-(BEDT-TTF)₂Cu₂(CN)₃^15,16, EtMe₃Sb[Pd(dmit)₂]₂^17,18, YbMgGaO₄^19,20,21,22 and 1T-TaS₂²³. Furthermore, spin-1 TLHAF Ba₃NiSb₂O₉ also shows QSL behaviors^24,25,26. QSL with spinon Fermi surface^27,28 was proposed and succeeded in understanding the QSL behaviors in such compounds^20,21,26. However, experimental realization of the QSL ground state in spin-1/2 TLHAF systems is still limited and remains an intriguing pursuit.

Recently, cluster magnet LiZn₂Mo₃O₈ has attracted considerable research interest as spin-1/2 TLHAF²⁹. Seven 4d electrons in a Mo₃O₁₃ cluster occupy their orbitals, resulting in one unpaired electron. Unpaired electron with spin S = 1/2 remains in the total symmetry of the Mo₃O₁₃ cluster (A₁ irreducible representation) with equal contributions from all three Mo atoms, and network of the magnetic clusters forms a uniform triangular lattice in LiZn₂Mo₃O₈. The dominant magnetic interaction between spin-1/2 Mo₃O₁₃ clusters is antiferromagnetic²⁹, yielding geometrical frustration. LiZn₂Mo₃O₈ is therefore an ideal 2D spin-1/2 TLHAF system. Magnetic susceptibility and heat capacity measurements suggested that 2/3 of S = 1/2 spins are quenched below 96 K, and condensed valence bond state (VBS) where resonance valence-bond states^30,31 coexist with remnant paramagnetic spins is proposed for the possible ground state^29,32. Gapless spin excitations were reported by electron spin resonance³², ⁷Li nuclear magnetic resonance (NMR)³², muon spin rotation (μSR)³², and inelastic neutron scattering (INS)³³ measurements. Emergent honeycomb lattice is theoretically proposed for the origin of the condensed VBS³⁴. Recently, a 1/6-filled extended Hubbard model in an anisotropic kagome lattice is also proposed to account for the low temperature phase of LiZn₂Mo₃O₈³⁵. However, intersite disorder between Li⁺ and Zn²⁺ ions is reported^29,32, which may affect on the intrinsic magnetism in LiZn₂Mo₃O₈.

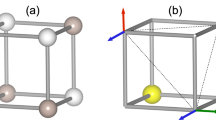
New molecular based triangular lattice systems Li₂AMo₃O₈ where A = In or Sc are of particular interest in this context^36,37. Li₂AMo₃O₈ crystallizes in a hexagonal structure P6₃mc, and no intersite disorder between Li⁺ and A³⁺ sites exists (see Supplementary Information). As in LiZn₂Mo₃O₈, spin-1/2 carrying Mo₃O₁₃ clusters are arranged on the structurally perfect triangular lattice separated by nonmagnetic Li and A layers in both compounds as shown in Fig. 1(a,b). Susceptibility measurements of both compounds report that the dominant magnetic interactions are antiferromagnetic and the effective moments are 1.61 μ_B (In) and 1.65 μ_B (Sc), which are close to p_eff = 1.73 μ_B the ideal value for spin S = 1/2. Spin-1/2 TLHAF is therefore realized in Li₂AMo₃O₈, whose ground states are however different from each other. In Li₂InMo₃O₈, long-range magnetic order develops below T_N = 12 K with Curie-Weiss temperature of Θ_CW = −242 K, and ⁷Li NMR study suggests that the magnetic structure is the 120° structure as described in Fig. 1(c). On the other hand, isostructural Li₂ScMo₃O₈ shows no long-range magnetic order down to 0.5 K in spite of large Weiss temperature of Θ_CW = −127 K. Instead, both magnetic susceptibility and heat capacity measurements indicate the development of short-range magnetic order below 10 K. Spin glass state is ruled out as the ground state of Li₂ScMo₃O₈ since the magnetic susceptibility shows no splitting between zero-field-cooling and field-cooling processes³⁷. Low-temperature heat capacity measurements in Li₂ScMo₃O₈ shows sizable T-linear term γ_mag = 35.7 mJ/mol · K², which is similar to those of QSL candidates κ-(BEDT-TTF)₂Cu₂(CN)₃¹⁶, EtMe₃Sb[Pd(dmit)₂]₂¹⁸, and Ba₃CuSb₂O₉³⁸. Furthermore, different magnetic entropies between Li₂ScMo₃O₈ and LiZn₂Mo₃O₈ suggests that the ground state in Li₂ScMo₃O₈ is QSL rather than condensed VBS. Because of easy access to two different ground states of spin-1/2 TLHAF, Li₂AMo₃O₈ is an intriguing system to investigate 2D spin-1/2 TLHAF. However, lack of microscopic measurements prevents us from fully understanding the ground states and dynamics of Li₂AMo₃O₈. In this paper, we investigate quantum magnetisms of polycrystalline Li₂InMo₃O₈ and Li₂ScMo₃O₈ by combination of μSR and time-of-flight (TOF) neutron scattering techniques.

Figure 1

(a,b) Crystal structure of Li₂AMo₃O₈. Li site is not depicted. (c) 120° spin structure on the Mo₃O₁₃-based triangular lattice in Li₂InMo₃O₈. Dashed lines in each panel represent the chemical unit cell.

Results and Discussion

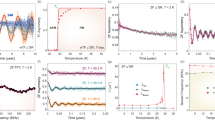
Zero field- (ZF-) μSR time spectra of Li₂InMo₃O₈ at several temperatures are shown in Fig. 2(a). The spectra show a damping at around 12 K, and spectral oscillations appear at lower temperatures. It is a direct evidence of the long-range magnetic order as reported in the earlier studies^36,37,39,40. Fourier transform of the spectrum at 3.33 K [see the inset of Fig. 2(a)] suggests that at least three different local fields are found in Li₂InMo₃O₈, which is probably due to crystallographically inequivalent muon stopping sites indicated by our density functional theory (DFT) calculation (see Supplementary Fig. S3 for Li₂ScMo₃O₈). The ZF-μSR spectra of Li₂InMo₃O₈ are fitted by three cosine functions with transverse and longitudinal relaxations

$${A}_{{\rm{ZF}}}(t)=\sum _{n=1}^{3}\,{A}_{n}\,[\frac{2}{3}\,\cos \,(2\pi {f}_{n}t+\varphi )\,\exp \,(\,-\,{\lambda }_{t}t)+\frac{1}{3}\,\exp \,(\,-\,{\lambda }_{l}t)]+{A}_{{\rm{BG}}}$$

(1)

where A_n and A_BG are the positron decay asymmetries of each oscillation (n = 1~3) and background (mainly from a silver backing plate) components, f_n is the precession frequency, ϕ is the initial phase, and λ_t (λ_l) is the transverse (longitudinal) relaxation rate. Fitting result at each temperature is shown in Fig. 2(a). Local magnetic fields of 84.9(3), 103.1(2), and 151.5(5) G are extracted at 3.33 K, and these values are comparable in magnitude of local fields that are observed in spin-1/2 magnets⁴¹. Figure 2(c) shows temperature dependences of f₁, f₂, and f₃, representing that long-range magnetic order evolves in Li₂InMo₃O₈ below T_N = 12 K with the critical exponents β ~ 0.33.

Figure 2

ZF- and LF-μSR results on Li₂AMo₃O₈. μSR time spectra of (a) Li₂InMo₃O₈ and (b) Li₂ScMo₃O₈. Solid lines in each panel represent the fitting curves (see the main text). A Fourier transform of the μSR time spectrum of Li₂InMo₃O₈ at 3.33 K (real amplitude) is plotted in the inset of (a). The inset of (b) shows a magnified view of the spectrum of Li₂ScMo₃O₈ at 0.07 K under H_LF = 1 kG. (c) Temperature dependences of local fields in Li₂InMo₃O₈ and Li₂ScMo₃O₈. (d) Temperature dependences of muon relaxation rates λ_f (left scale) and λ_s (right scale) of Li₂ScMo₃O₈ under longitudinal field. Solid line is calculated λ (right scale) using Eq. (7).

In the meanwhile, ZF-μSR time spectrum of Li₂ScMo₃O₈ at 0.07 K shows a highly damped oscillation with a pronounced reduction of the 1/3 tail as described in Fig. 2(b). To see the temperature evolution of the local fields in Li₂ScMo₃O₈, the ZF-μSR spectrum are fitted by combination of transverse and longitudinal relaxations

$${A}_{{\rm{ZF}}}(t)={A}_{1}\,\cos \,(2\pi {f}_{{\rm{Sc}}}t+\varphi )\,\exp \,(\,-\,{\lambda }_{t}t)+{A}_{2}\,\exp \,(\,-\,{\lambda }_{l}t)+{A}_{{\rm{BG}}}.$$

(2)

The fitting result at each temperature is plotted in Fig. 2(b), and temperature dependence of the local field f_Sc is also plotted in Fig. 2(c). One can clearly see the temperature evolution of f_Sc below 4 K with the critical exponent β ~ 0.28 which is similar to those of Li₂InMo₃O₈. Therefore, magnetic nature of these compounds are essentially the same, but it should be noted that the ground state of Li₂ScMo₃O₈ is short-range magnetic order by considering the strong damping of the oscillation below 4 K. The anomaly at 4 K was also found in the temperature derivative of the magnetic susceptibility³⁷. Although the short-range magnetic order develops in Li₂ScMo₃O₈ below 4 K, the spectrum shows a moderate tail over a long period of time, suggesting that spin fluctuation survives even at 0.07 K. To explicitly distinguish the spin fluctuation of the Mo₃O₁₃ cluster, we performed longitudinal field- (LF-) μSR measurements on Li₂ScMo₃O₈ under longitudinal magnetic field (H_LF) of 1 kG. Figure 2(b) and its inset display a LF-μSR time spectrum measured at 0.07 K. H_LF = 1 kG seems to be sufficient to quench (decouple) muon spin relaxations by both nuclear dipoles and the short-range ordered state. The characteristic LF-μSR spectrum of Li₂ScMo₃O₈ at 0.07 K was fitted by the following equation

$${A}_{{\rm{LF}}}(t)={A}_{{\rm{f}}}\,\exp \,(\,-\,{\lambda }_{f}t)+{A}_{{\rm{s}}}\,\exp \,(\,-\,{\lambda }_{{\rm{s}}}t)+{A}_{{\rm{BG}}}$$

(3)

where A_f and A_s are asymmetries of fast (λ_f) and slow (λ_s) relaxation components, respectively (A_f + A_s = 0.16), and A_BG is the background asymmetry (A_BG = 0.03). The fitting results are described by the solid lines in Fig. 2(b) and its inset. We also fit LF-μSR time spectra under H_LF = 1 kG at several temperatures, and obtained temperature dependences of λ_f and λ_s are plotted in Fig. 2(d). λ_f shows a rapid relaxation with relative signal amplitude of ~3%. It mainly corresponds to the remnant signal from the short-range ordered state since λ_f exhibits a steep increase at 4 K as temperature goes down. On the other hand, λ_s shows a slow relaxation with two orders of magnitude less than λ_f, which is related to the intrinsic spin fluctuation of the Mo₃O₁₃ cluster. Remarkably, temperature dependence of λ_s shows a temperature-independent plateau below 1 K and converges into the finite value of ~0.002 μs⁻¹ which is very close to that of triangular lattice QSL 1T-TaS₂ (λ = 0.0023 μs⁻¹ at 0.07 K)²³. Indeed, such low-temperature plateau behaviors of muon relaxation rate is common feature in the TLHAF QSL candidates^20,25, which will be discussed again. To obtain complementary information to our μSR results on Li₂AMo₃O₈, TOF neutron scattering measurements were also conducted.

Elastic neutron scattering spectra of Li₂InMo₃O₈ below and above T_N are shown in Fig. 3(e). A magnetic Bragg peak appears at momentum transfer Q = 0.719(1) Å⁻¹ below T_N. The Q position corresponds to (1/3, 1/3, 0), indicating the 120° magnetic structure consistent with the previous ⁷Li-NMR measurements³⁷. By comparing the intensity of the magnetic peak with those of nuclear Bragg peaks, the ordered moment at 4.6 K is estimated to be 0.51(3) μ_B. Theoretically, the magnetic moment is reduced by about 59% for the spin-1/2 TLHAF⁶, which is close to the observed ordered moment (reduced by 49% assuming g = 2). The reduced moment originates in a combination of geometrical frustration and quantum fluctuation. Neutron scattering intensity (I) map from Li₂InMo₃O₈ as a function of Q and energy transfer ($\hslash \omega$) at 4.5 K (<T_N) is shown in Fig. 3(a). Dispersive excitation centered at the magnetic zone center (1/3, 1/3, 0) was observed. Because of the Q position, the excitation is assigned to be the spin wave excitation in the long-range magnetic ordered state. Energy spectrum at the magnetic zone center exhibits a substantial peak at $\hslash \omega =2.08(3)$ meV as shown in Fig. 3(f). This result claims that one branch (or some branches) of the spin wave excitation has spin gap at the magnetic zone center due to the magnetic anisotropy. On the other hand, magnetic signals at the magnetic zone center become quasielastic above T_N as shown in Fig. 3(b,f). Therefore, the gap-like excitation is a characteristic feature of the long-range magnetic ordered state. To observe the whole structure of the spin wave excitation at 4.5 K, $I(Q,\hslash \omega )$ map using higher E_i is presented in Fig. 3(c). The spin wave excitation survives up to ~9 meV. Q dependences of the spin wave intensities at various $\hslash \omega$s are plotted in Fig. 3(g). The spectra are asymmetric at $\hslash \omega > 3.0$ meV, and the peak shifts to lower Q at higher $\hslash \omega$. This result suggests that the squared magnetic form factor (|F(Q)|²) of the Mo₃O₁₃ cluster decreases quickly and is negligible at high Q, representing the unpaired electron with equal contributions from all three Mo atoms in Li₂InMo₃O₈.

Figure 3

TOF neutron scattering results on Li₂InMo₃O₈. Low-energy inelastic neutron scattering intensity maps at (a) 4.6 K and (b) 13.5 K measured with E_i = 11.9 meV. (c) High-energy inelastic neutron scattering intensity map at 4.6 K measured with E_i = 22.0 meV. (d) Calculated inelastic neutron scattering intensity map at 4.6 K using the optimum parameters as described in the main text. Calculated energy resolution for E_i = 11.9 meV was convoluted. (e) Elastic neutron scattering intensities at 4.6 and 18.7 K with energy window of [−0.15, 0.15] meV. Solid lines represent the fitting result using the Gaussian function with linear background. (f) Energy spectra integrated over Q = [0.69, 0.77] Å⁻¹ at 4.6 and 13.5 K measured with E_i = 11.9 meV. (g) Q dependences of the neutron scattering intensities at several energy windows. Each energy window was [1.5, 2.0], [2.0, 2.5], [2.5, 3.0], [3.0, 3.5], and [3.5, 4.0] meV with E_i = 11.9 meV (red), [4.0, 4.5] and [4.5, 5.0] meV with E_i = 15.8 meV (blue), [5.0, 6.0] and [6.0, 7.0] meV with E_i = 22.0 meV (green), and [7.0, 8.0] meV with E_i = 32.7 meV (black), respectively. Constant background was subtracted from each Q dependence. Solid lines are calculated results using the optimum parameters in Eq. (5).

For quantitative analysis on the spin wave excitation in Li₂InMo₃O₈, semi-classical linear spin wave (LSW) analysis was performed considering the 120° spin structure on the spin-1/2 2D Mo₃O₁₃-based triangular lattice [Fig. 1(c)]. The gap-like excitation at the magnetic zone center in the long-range magnetic ordered state is also observed in the other spin-1/2 triangular lattice system Ba₃CoSb₂O₉¹³, and the peak energy (E₀) roughly scales with T_N in these compounds: E₀ = 0.65 meV and T_N = 3.8 K in Ba₃CoSb₂O₉¹³ whereas E₀ = 2.08 meV and T_N = 12 K in Li₂InMo₃O₈. This suggests that the origin of the gap-like excitation in Li₂InMo₃O₈ is the same as that in Ba₃CoSb₂O₉¹³. Therefore, as in Ba₃CoSb₂O₉^12,13,14, the nearest-neighbor anisotropic exchange interaction was considered as the model Hamiltonian for Li₂InMo₃O₈

$$ {\mathcal H} =\alpha J\,\sum _{i,j}\,({S}_{i}^{x}{S}_{j}^{x}+{S}_{i}^{y}{S}_{j}^{y}+\delta {S}_{i}^{z}{S}_{j}^{z})$$

(4)

where α, J, and δ represent the renormalization factor, the nearest neighbor exchange coupling constant, and the anisotropic factor. J was fixed to 112 K determined by the magnetic susceptibility measurement³⁷. By fitting the calculated powder-averaged Q dependences to the experimental results at different $\hslash \omega$s (2~7.5 meV) simultaneously, optimum parameters were yielded

$$\begin{array}{rcl}\alpha & = & 0.56(1),\\ \delta & = & 0.975(1).\end{array}$$

(5)

Fitting results together with the experimental results are shown in Fig. 3(g), and calculated LSW $I(Q,\hslash \omega )$ map is also shown in Fig. 3(d). Satisfactory agreements with calculation and experiment were confirmed. Obtained α is smaller than 1, indicating a negative quantum renormalization effect theoretically proposed for 2D spin-1/2 TLHAF^42,43,44. Similar negative quantum renormalization effect (α ~ 0.65) was also reported in Ba₃CoSb₂O₉¹⁴. Therefore, observed magnetic excitations of Li₂InMo₃O₈ in the accessible $(Q,\hslash \omega )$ region are well understood by the semi-classical LSW theory assuming the 120° magnetic structure on the spin-1/2 Mo₃O₁₃ triangular lattice.

In contrast to Li₂InMo₃O₈, no magnetic Bragg peak evolves in the elastic channel down to 0.3 K in Li₂ScMo₃O₈ as plotted in Fig. 4(c), in agreement with our μSR results. On the other hand, diffuse scattering expected for the short-range order is not observed in our neutron measurements. Strong incoherent scattering may smear out such magnetic diffuse scattering in Li₂ScMo₃O₈. Figure 4(a) depicts $I(Q,\hslash \omega )$ map at 0.3 K. Clear diffuse scattering was observed in the inelastic channel. Although both magnetic excitations in Li₂InMo₃O₈ and Li₂ScMo₃O₈ are centered at Q ~ 0.7 Å⁻¹ [Figs 3(a) and 4(a)], the overall structures are different, representing their different ground states. In Li₂ScMo₃O₈, steep continuum excitation was observed. The Q dependences of the magnetic excitations are invariant in the different energy windows as shown in Fig. 4(d). Steep continuum excitation, or spinon continuum, is the common feature of the magnetic excitations in the QSL candidates^{3,21,22,26,45}. $I(Q,\hslash \omega )$ map at high temperature (22 K) is also shown in Fig. 4(b). Although overall magnetic fluctuation at 22 K is similar to that at 0.3 K, there are some differences. Scattering intensity decreases at 22 K. In addition, as shown in Fig. 4(e), spectrum weight of the Q dependence at 2 meV slightly shifts to Q = 0 at high temperature, which is also observed in other QSL candidates^22,26,45.

Figure 4

TOF neutron scattering results on Li₂ScMo₃O₈. Inelastic neutron scattering intensity maps with E_i = 10.3 meV measured at (a) 0.3 K and (b) 22 K. (c) Elastic neutron scattering intensities with energy window of [−0.075, 0.075] meV at 0.3 and 22 K with E_i = 10.3 meV. (d) Q dependences of the neutron scattering intensities at several energy windows at 1.7 K. Each energy window was [1.5, 2.5] meV with E_i = 7.5 meV, [2.5, 3.5] meV with E_i = 10.3 meV, [3.5, 4.5] meV with E_i = 15.0 meV, and [4.5, 5.5] meV with E_i = 23.9 meV, respectively. (e) Q dependences of the neutron scattering intensities with [1.5, 2.5] meV at 0.3 and 22 K using E_i = 7.5 meV. (f) Dynamical spin susceptibilities at Q = [0.6, 0.8] Å⁻¹ for 0.3, 10, 22, and 40 K. Solid lines are the fitting results by the quasielastic Lorentzian as described in the main text. (g) Temperature dependences of static spin susceptibility χ′ (left scale) and relaxation rate Γ (right scale) obtained by the fitting in panel (f). Solid line is a scaled bulk magnetic susceptibility (χ_bulk = M/H) measured with H = 1 T.

To investigate in more detail the characteristic energy (or time) scale of the steep continuum in Li₂ScMo₃O₈, the dynamical spin susceptibilities $\chi ^{\prime\prime} (\hslash \omega )=[1-\exp (\,-\,\hslash \omega /{k}_{B}T)]/|F(Q){|}^{2}I(\hslash \omega )$ at Q = [0.6, 0.8] Å⁻¹ where the magnetic signal is maximal are plotted for different temperatures in Fig. 4(f). The spectra are well fitted by the quasielastic Lorentzian $\chi ^{\prime\prime} (\hslash \omega )=\chi ^{\prime} \hslash \omega {\rm{\Gamma }}/[{(\hslash \omega )}^{2}+{{\rm{\Gamma }}}^{2}]$ where χ′ is the static susceptibility and Γ the spin relaxation rate [or peak position of $\chi ^{\prime\prime} (\hslash \omega )$]. The temperature dependences of the resulting parameters are shown in Fig. 4(g). Upon decreasing temperature, Γ decreases while χ′ increases. Contrary to the conventional long-range ordered magnets, no divergent behavior was observed in the temperature dependences of χ′ and Γ. It should be noted that χ′ scales with bulk magnetic susceptibility χ_bulk over the temperature range of 3 ≤ T ≤ 40 K [see solid line in Fig. 4(g)] and Γ is also scaled by the muon relaxation rate λ_s as discussed below. These fittings also extract two important features of the steep continuum in Li₂ScMo₃O₈: (1) the magnetic excitation is gapless consistent with the heat capacity measurement³⁷ and (2) the dynamical spin susceptibility extends from the elastic channel up to at least 9.5 meV which is about 1.6 J where J (=67 K) is determined by the magnetic susceptibility measurement³⁷.

Complementary analysis of μSR and INS results enables us to exclusively clarify the quantum fluctuations in Li₂ScMo₃O₈. Muon spin relaxation rate λ_s in Fig. 2(d) is related to the spin relaxation rate of the magnetic fluctuation Γ in Fig. 4(g) on the basis of following Redfield’s formula⁴⁶

$$\lambda =\frac{2{({\gamma }_{\mu }{\delta }_{\mu })}^{2}{\rm{\Gamma }}}{{({\gamma }_{\mu }{H}_{{\rm{LF}}})}^{2}+{{\rm{\Gamma }}}^{2}}$$

(6)

where γ_μ and δ_μ are the gyromagnetic ratio of muon (=2π × 135.54 MHz/T) and average distribution of local magnetic fields at muon sites. We performed electrostatic potential calculations using a point-charge model⁴⁷ and estimated δ_μ = 204.8 G for Li₂ScMo₃O₈ (see Supplementary Information). Since H_LF (=1 kG = 8.5 × 10⁸ Hz) is much smaller than Γ (=2.7 meV = 6.5 × 10¹¹ Hz at 0.3 K) in Li₂ScMo₃O₈, Eq. (6) is reformulated as

$$\lambda \sim \frac{2{({\gamma }_{\mu }{\delta }_{\mu })}^{2}}{{\rm{\Gamma }}}.$$

(7)

We plotted calculated temperature dependence of λ using Γ obtained by our INS measurements and compared with λ_s obtained by our LF-μSR measurements [see solid line for calculation and circles for μSR results in Fig. 2(d)]. Quantitative agreement can be seen; the anomaly around 4 K is artificial feature owing to λ_f. Therefore, both μSR and INS measurements exhibit that quantum fluctuations persist at the lowest measured temperature. As mentioned above, such low-temperature plateaus of the relaxation rates were widely observed in the triangular-lattice^20,25 and kagome-lattice^{45,48,49,50,51} QSL candidates.

To account for the QSL-like excitations in Li₂ScMo₃O₈, we now consider the spinon Fermi surface QSL model. In Li₂ScMo₃O₈, no static long-range order was detected even down to 0.07 K [Figs 2(b) and 4(c)]. Alternatively, gapless continuum in Li₂ScMo₃O₈ was observed at Q = 0.726(4) Å⁻¹ corresponding to the (1/3, 1/3, 0) position [Fig. 4(a,d,f)]. Moreover, both λ_s and Γ exhibit temperature-independent plateaus at low temperature [Figs 2(d) and 4(g)]. These features are well explained by QSL with spinon Fermi surface^27,28. As discussed in earlier works^20,21,26, the spinon Fermi surface QSL model on the spin-1/2 TLHAF expects that (1) absence of static long-range magnetic order, (2) muon spin relaxation rate approach a finite value as temperature approaches zero, (3) magnetic excitation is gapless continuum, and (4) $\chi ^{\prime\prime} (Q,\hslash \omega )$ shows the maximum intensity at the corner of the 2D Brillouin zone [e.g. (1/3, 1/3, 0)]. All observed features of the magnetic fluctuation in Li₂ScMo₃O₈ can be well described by the spinon Fermi surface QSL model. Although the second peak of the spinon continuum in Ba₃NiSb₂O₉ was also observed at (2/3, 2/3, 0)²⁶, the second peak in Li₂ScMo₃O₈ was not detected at (2/3, 2/3, 0) corresponding to Q = 1.45 Å⁻¹ as shown in Fig. 4(d) because of the quick decay of the squared magnetic form factor of the Mo₃O₁₃ cluster³³. By performing complementary analysis on μSR and INS results, we conclude that Li₂ScMo₃O₈ undergoes the short-range magnetic order below 4 K with the QSL-like fluctuations which persist down to the lowest temperature.

We compare the Mo₃O₁₃-cluster-based triangular lattice antiferromagnets, Li₂AMo₃O₈ and LiZn₂Mo₃O₈, in line with the recent theory by Chen et al.³⁵. They proposed a 1/6-filled Hubbard model on an anisotropic kagome lattice with the nearest-neighbor electron hopping and repulsions³⁵ to account for the magnetism in LiZn₂Mo₃O₈²⁹. Electron is fractionalized into charged boson and spin-carring spinons; plaquette charge order emerges as the charge ground state and the spin degree of freedom can be then described by U(1) QSL with spinon Fermi surface, which can explain the unusual magnetic susceptibility in LiZn₂Mo₃O₈²⁹. For comparison with different compounds, they introduce a phenomenological parameter ξ to characterize the anisotropy of the Mo kagome lattice: ξ = d_inter/d_intra where d_intra (d_inter) is the intracluster (intercluster) Mo-Mo bond length. Large anisotropy ξ tends to suppress charge fluctuations between clusters leading to the 120° long-range magnetic order whereas small anisotropy ξ corresponds to large charge fluctuation generating the U(1) QSL with spinon Fermi surface. Using the structural parameters summarized in Supplementary Information, we estimated ξ as 1.271, 1.269, and 1.258 for Li₂InMo₃O₈, Li₂ScMo₃O₈, and LiZn₂Mo₃O₈²⁹, respectively. The phenomenological parameter ξ explains the different ground states between the 120° long-range magnetic order in Li₂InMo₃O₈ and the condensed VBS in LiZn₂Mo₃O₈. However, the ξ values of Li₂InMo₃O₈ and Li₂ScMo₃O₈ are very close to each other in spite of their different ground states. Nevertheless, ¹¹⁵In and ⁴⁵Sc NMR measurements on Li₂AMo₃O₈ reported that charge fluctuation in Li₂ScMo₃O₈ is 2.6 times larger than that in Li₂InMo₃O₈⁵², and the difference between charge fluctuations can qualitatively explain the different ground states of Li₂InMo₃O₈ and Li₂ScMo₃O₈. Therefore, the anisotropic parameter for the Mo kagome lattice, ξ, is too simplified to explain the different ground states in Li₂AMo₃O₈, and more detailed parameter is required for Li₂AMo₃O₈.

We also compare the magnetic excitations in Li₂InMo₃O₈ and Li₂ScMo₃O₈ to discuss the origin of the different ground states. Although both magnetic excitations in Li₂InMo₃O₈ and Li₂ScMo₃O₈ center at Q ~ 0.72 Å⁻¹, low-energy magnetic excitations show opposite behaviors. The magnetic excitation at the magnetic zone center in Li₂InMo₃O₈ clearly exhibits the peak at 2.08(3) meV [Fig. 3(a,f)]. Our LSW analysis suggests that the anisotropic exchange interaction is necessary to reproduce the peak. Meanwhile, the gapless magnetic excitation in Li₂ScMo₃O₈ indicates that magnetic anisotropy is negligibly small in Li₂ScMo₃O₈ [Fig. 4(a,f)]. Thus, the difference in the magnetic anisotropy is another possibility of the origin of the different ground states in Li₂AMo₃O₈. In fact, the gap-like excitation was observed in the long-range ordered state of Ba₃CoSb₂O₉^13,14, whereas the gapless magnetic excitations in the QSL systems YbMgGaO₄^21,22 and Ba₃NiSb₂O₉²⁶. INS measurements on magnetic excitations in the substitution system Li₂(In_1−xSc_x)Mo₃O₈⁴⁰ are effective to further elucidate the origin of different magnetic ground states, which is left for future work.

Conclusion

We performed a comprehensive study on the quantum magnetisms in the Mo₃O₁₃-cluster-based spin-1/2 triangular lattice antiferromagnets, Li₂InMo₃O₈ and Li₂ScMo₃O₈ by means of μSR and TOF neutron scattering techniques. Spin wave excitation in Li₂InMo₃O₈ was well described by the nearest neighbor anisotropic Heisenberg model based on the 120° spin structure. Li₂ScMo₃O₈ exhibits the short-range magnetic order below 4 K with the QSL-like fluctuations which persist down to the lowest temperature. The origin of the different magnetic ground states in Li₂AMo₃O₈ is discussed in terms of anisotropies of crystal structures and magnetic interactions.

Methods

The preparation of polycrystalline Li₂InMo₃0₈ (Li₂ScMo₃O₈) was carried out by two steps³⁷. First, to synthesize a precursor Li₂MoO₄, a mixture with a ratio of MoO₃:Li₂CO₃ = 1:1 was ground, placed in an alumina crucible, and heated at 873 K for 24 hours in air; we repeated this step for three times. Then, a mixture having a ratio of In₂O₃ (Sc₂O₃):Li₂MoO₄:MoO₃:Mo = 0.5:1:0.84:1.16 was ground, pressed into a pellet, sealed in an evacuated quartz tube, heated at 923 K for 12 hours, and heated at 1198 K (1173 K) for 24 hours; we repeated this step for two times. Magnetization measurements were performed using a commercial superconducting quantum interference device (SQUID) magnetometer (Quantum Design Magnetic Property Measurement System, MPMS). ZF- and LF-μSR experiments were performed using the Advanced Research Targeted Experimental Muon Instrument at the S1 line spectrometer (ARTEMIS)⁵³ with a conventional ⁴He flow cryostat and the D1 spectrometer⁵³ with a ³He-⁴He dilution refrigerator installed at Materials and Life Science Experimental Facility (MLF), Japan Proton Accelerator Research Complex (J-PARC). We used the VASP software⁵⁴ for DFT calculation and the DipElec program⁴⁷ to calculate the local magnetic fields in Li₂ScMo₃O₈. TOF neutron scattering measurements were performed using the Fermi chopper spectrometer 4SEASONS at MLF, J-PARC⁵⁵. Frequencies of the Fermi chopper were 350 and 250 Hz for the In and Sc systems, resulting in the combinations of incident neutron energies of 11.9, 15.8, 22.0, and 32.7 meV, and 7.5, 10.3, 15.0, and 23.9 meV⁵⁶, respectively. A standard top-loading cryostat at 4SEASONS was used for the measurements on Li₂InMo₃O₈, whereas a ⁴He refrigerator and a ³He cryostat were used for Li₂ScMo₃O₈. Empty can was measured at corresponding temperatures, and then subtracted from raw data of Li₂ScMo₃O₈. TOF data were visualized by software suite Utsusemi⁵⁷. Neutron scattering intensities are converted to the absolute unit using the incoherent scattering of each sample⁵⁸ after correction of the neutron absorption effect. Squared magnetic form factor of the Mo₃O₁₃ cluster³³ and $\hslash \omega$-dependent energy resolution at 4SEASONS⁵⁹ were included in the LSW calculations for Li₂InMo₃O₈.