Abstract
Distance, environmental heterogeneity and local adaptation can strongly influence population structure and connectivity. Understanding how these factors shape the genomic landscape of threatened species is a major goal in conservation genomics and wildlife management. Herein, we use thousands (6,859) of single nucleotide polymorphism markers and spatial data from hundreds of individuals (n = 646) to re-evaluate the population structure of Agassiz’s desert tortoise (Gopherus agassizii). Analyses resolve from 4 to 8 spatially well-defined clusters across the range. Western, central, and southern populations within the Western Mojave recovery unit are consistent throughout, while analyses sometimes merge other recovery units depending on the level of clustering. Causal modeling consistently associates genetic connectivity with least-cost distance, based on multiple landscape features associated with tortoise habitat, better than geographic distance. Some features include elevation, soil depth, rock volume, precipitation, and vegetation coverage, suggesting that physical, climatic, and biotic landscape features have played a strong evolutionary role restricting gene flow between populations. Further, 12 highly differentiated outlier loci have associated functions that may be involved with neurogenesis, wound healing, lipid metabolism, and possibly vitellogenesis. Together, these findings have important implications for recovery programs, such as translocations, population augmentation, reproduction in captivity and the identification of ecologically important genes, opening new venues for conservation genomics in desert tortoises.
Similar content being viewed by others
Introduction
A major goal in conservation genetics involves understanding how landscape features influence population connectivity and structure1,2. Heterogeneous environments, geographic distance and life-history traits, such as longevity, mating behavior, and potential for dispersal, can affect rates of gene flow across a species’ range. Agassiz’s desert tortoises (Gopherus agassizii) are long-lived, have low-motility, and inhabit one of the most arid environments in North America3,4. Populations of G. agassizii have been assessed genetically5,6,7,8,9,10 since the species was prioritized for conservation11,12. One focus has been the redefinition and delineation of recovery units, originally proposed in the Desert Tortoise Recovery Plan12, based on clustering methods from population genetic data. While some patterns of population genetic structure have been resolved consistently, marked differences in experimental design, numbers of samples, and sampling strategies fostered inconsistent results, in particular with respect to the resolution of the Western Mojave recovery unit9,10,12.
Previous studies have recognized the importance of isolation-by-distance (IBD) as a factor modulating genetic connectivity among desert tortoises9,10,13,14. IBD is an evolutionary process by which genetic differences between individuals and/or populations increase with geographic distance15,16. The main biological assumption is that many organisms have limited dispersal leading to geographically restricted mating. While geographic distance is an important part the landscape, it is insensitive to the environment, which can be an important source of divergence17,18. Isolation-by-environment (IBE) and isolation-by-resistance (IBR) are two ways in which the effects of landscape heterogeneity can be measured with respect to genetic connectivity. Because IBR can conflate both IBE and IBD in empirical data17, it can be desirable to explicitly test for IBE, together with IBR and IBD, to untangle multiple competing patterns. A means to accomplish this is to treat IBD as the null hypothesis, against which multiple IBE and IBR models can be tested. While IBE models use overall environmental distances, IBR uses environmental friction or resistance as a proxy for probability of dispersal, where lower resistance leads to higher dispersal16. Environmental friction can be quantified by the least-cost distance (LCD), which is the path between two points that accumulates less friction and resistance-distance (RD), which uses circuit-theory to simultaneously weigh many possible routes across a landscape18.
Landscape genetics models on G. agassizii have reported stronger support for IBD than for IBR13,14. However, at a fine spatial scale (<100 km2), Latch et al.14 found weak population structure and weak influence of natural (e.g., slope) and anthropogenic (e.g., roads) factors on genetic connectivity in one population in the central Mojave Desert. Over a broader scale, Hagerty et al.13 used habitat suitability scores from a model of the distribution of desert tortoises19 to quantify landscape friction with LCD and RD. Their results suggested distance due to barriers, such as mountains and deep valleys, are major landscape features limiting gene flow. However, their barrier model was not better than the null IBD expectation13. Moreover, these landscape genetic studies have relied on Mantel tests to identify explanatory variables, a method which has been heavily critiqued20,21,22. After comparing a suite of popular methods for assessing spatial correlation, Shirk et al.23 suggested that linear mixed-effect models using maximum-likelihood population effects24 and reciprocal causal modeling16,25 were among the most consistent methods; these have not been applied yet for desert tortoises. Furthermore, previous studies on tortoises have relied on at most 20 selectively-neutral microsatellite markers, which inform only about random, stochastic changes in allele frequencies. Genome-wide single nucleotide polymorphisms (SNPs), alternatively, are generally more abundant and can potentially inform about adaptive processes acting upon specific alleles26,27.
The genome era promises to resolve many conservation genetics issues associated with breadth of data, marker evolution (e.g., neutral vs. selected sites) and scalability27. For instance, thousands of selectively neutral markers can accurately estimate effective population sizes (minimum number of genetically viable individuals) and migration rates (frequency of inter-individual gene exchange), both of which are evolutionary measures critical for assessing conservation status. Further, genomic sites under selection can identify adaptations associated with geographic features, adding potential links to the environment27,28. Landscape genomics extends the amalgamation of population genetics and landscape ecology (landscape genetics) on two fronts: (1) access to thousands of putatively independent markers across the genome, which should increase analytical accuracy; and (2) access to genetic data that may be subject to evolutionary forces other than drift, such as natural selection and linkage29. The distribution of genetic variation across landscapes can reflect intricate interactions between the environment and evolutionary processes affecting population structure and adaptation to local conditions30.
The recently published genome of G. agassizii provides a unique resource to study the genomic basis of desert adaptations, and factors related to health, disease, and longevity31. Likewise, such data can facilitate population genomic analyses by serving as a reference for mapping variants that can be linked to functional regions. Reduced-representation-sequencing approaches, such as double-digest restriction-site associated sequencing (ddRAD-seq), are rapid, reliable, and cost-effective for generating thousands of SNPs across the genome for hundreds of individuals32. These approaches may significantly advance evolutionary and conservation analyses for many species28,33.
Herein, we report an analysis of ddRAD-seq data comprising thousands of markers for hundreds of Agassiz’s desert tortoises. Our aim is to comprehensively re-assess population structure throughout the species’ range and provide an understanding of how landscape features influence genetic connectivity. We also seek to associate outlier loci with the functions of neighboring genes and model their distribution in an attempt to better understand local adaptation using reverse ecology. Lastly, we anticipate that our results will better inform wildlife management decisions for recovering declining desert tortoise populations34.
Materials and Methods
Sampling
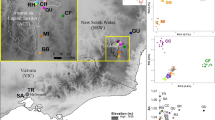
We evaluated 538 samples of G. agassizii from the Marine Air Ground Task Force Training Command, Marine Corps Air Ground Combat Center, Twentynine Palms, California. These samples came mainly from 23 locations in the southern Mojave region. In addition, we used archival DNA samples employed in Murphy et al.9 (n = 494), which came from hand-captured tortoises whose blood was salvaged from other research projects7,35,36,37. For these, samples were collected at 31 locations across the Mojave and Colorado deserts (electronic Supplementary File S1), except for Nevada and the Beaver Dam Slope in Utah9 (Fig. 1). In total, 1032 samples were processed. In the field, animal-handling procedures followed federal and state protocols which adhered to U.S. Fish and Wildlife Service guidelines. Samples were collected under research permits from the California Department of Fish and Game and U.S. Fish and Wildlife Service (TE-06556, TE-17730, BO 8-8-11-F-65R), and complied with the Animal Care and Use Committee of the U.S. Geological Survey and the Animal Research Committee at the University of California, Los Angeles.
Map of the area with orographic and hydrological details that might act as barriers. USFWS12 recovery units are delineated in white. Points represent samples used in this study and are colored by the populations inferred by Murphy et al.9. The hillshade effect was computed using the hillShade function in the R package raster46 after extracting slope and aspect rasters from elevation data at a resolution of 3.6 arc seconds (USGS, and Japan ASTER Program, 2011, SC:ASTGTM.002:2088835414, 1B, USGS, Sioux Falls, 2011-10-07, downloaded from https://earthexplorer.usgs.gov/). The map was generated with the R package raster v2.6 (https://cran.r-project.org/web/packages/raster/index.html).
Laboratory procedures and next-generation sequencing
Total genomic DNA was isolated from 50–100 µl of whole blood in 750 µl lysis buffer (50 mM Tris pH 8.0; 50 mM EDTA; 25 mM Sucrose; 100 mM NaCl; 1% SDS) by overnight lysis with proteinase K at 55 °C, followed by robotic extraction using a QIAGEN BioSprint 96 robotic magnetic-particle purification system (Qiagen, Valencia, California, USA) and Invitrogen Dynal bead extraction chemistry (Life Technologies, Carlsbad, California, USA). The recovered DNA was quantified using a BioTEK Synergy HT (BioTEK, Vermont, USA) and diluted working stocks to 5 ng/μl in Low TE (10 mMTris-pH 8.0, 0.1 mM EDTA). Genotyping was performed at the University of Arizona Genetics Core following the protocol of Peterson et al.32. In brief, genotyping consisted of cutting genomic DNA with two restriction endonucleases (SphI and MluCI), followed by size-selection, PCR amplification, quantification, and adaptor ligation. Barcode adapters, which recognized individual samples, were ligated to each fragment. Samples were pooled as equimolar concentrations, having 43–48 samples per pool (7 pools per sequencing lane). Libraries were later massively pair-ended sequenced using 4-5 flow-cell lanes with Illumina HiSeq2500 at a read length of 100 bp.
Bioinformatics
Sequences were retrieved from the University of Arizona Genetics Core server and transferred to SciNet, a high-performance computing server at the University of Toronto. All Illumina pair-end sequence data were filtered for quality control, de-multiplexed (separated and clustered into groups of reads based on individual-level sequence tags) and assembled using Stacks v1.4438, a software package for restriction-site associated sequencing analysis. Raw reads were initially processed with the program process_radtags, filtering all reads with at least one uncalled base (-c option), reads with at least 10% of their length (about 10 bp) having contiguous low-quality bases (<20 Phred score; options: -q -w 0.1 -s 20), and recovering ambiguous barcode tags (-r option). De-multiplexing involved looking for a four-base in-read barcode tag, followed by the restriction site of sphI on forward reads (–renz_1 sphI), and the restriction site of mluCI (–renz_1 mluCI) on the reverse end, and the Illumina library index in the FASTQ header (–inline_index). Next, de-multiplexed sequences were mapped (locally aligned) to the reference genome of G. agassizii31 using Bowtie239 and the following settings: -D 15 -R 2 -N 0 -L 20 -i S,1,0.75. The resulting sequence alignment/map file was converted to binary data, sorted, and indexed with Samtools v1.3.140. Locus identification, cataloging, and re-matching were performed with pstacks, cstacks, and sstacks, respectively. Only stacks with a read depth of ≥5 (-m in pstacks) were kept. For cataloging, loci were determined by genomic position (-g), allowing a maximum of 3 mismatches per sample locus (-n in cstacks). A variant-call format file was generated by the program populations (Stacks) reporting all variable sites per locus (e.g., scaffold/contig); loci found in at least 50% of the samples were retained. In a second filtering step, SNPs with a minor allele frequency below 0.001 were excluded, retaining the SNP with the highest minor allele frequency per linkage group (scaffold) using a Perl script (https://github.com/santiagosnchez/sing_snp_vcf).
Population structure
We assessed population structure with Admixture41, which can efficiently handle thousands of SNPs and uses a block relaxation algorithm that accurately estimates ancestry coefficients per individual. To select the best genetic group size (K), 10 bootstrap runs were executed using a 5-fold cross-validation (50 cross-validations per K) for K values ranging from 1 to 10. Only the K cluster with the smallest cross-validation error and significantly (Wilcoxon rank sum test) different bootstrapped cross-validation distributions was used for subsequent analyses; other K clusters that were only marginally worse were reported. Q-matrices were imported into R v3.442 and bar plots with stacked proportions of ancestry per individual were generated.
In addition to Admixture, a discriminant analysis of principal components (DAPC)43 was performed using the R package adegenet44. The discriminant analysis of principal components used ordination to graphically depict total genetic variation, maximizing between-group genetic variation, while minimizing within-group variation. Given that the analyses did not allow inclusion of missing data, missing genotypes were substituted for the mean of the available data per locus, where allelic data represented allelic counts separated into two columns (e.g., for a homozygote AA, heterozygote AT, and homozygote TT, the genotypes would be represented as [2,0], [1,1], and [0,2], respectively). DAPC required the a priori selection of both the number of retained principal components (PCs) and the number of discriminant functions. Thus, analyses ran a 50-fold cross-validation with data separated into training (90%) and testing (10%) sets (maximum number of retained PCs = 100) using the function xvalDapc in adegenet. Afterwards, the optimization with the best trade-off between retaining too few or too many principal components was selected. Ordinated genetic distances were then visualized in a scatter plot and colored by genetic cluster in R42.
Spatial interpolation of ancestry coefficients
The Q-matrix generated by Admixture was used to predict ancestry coefficients on a spatial grid. An R implementation of Kriging interpolation (the Krig function from the package fields45) was applied using a scaling theta of 1, assuming that the unknown covariance was a realization of a Gaussian random spatial processes. To improve model predictions, 200 random locations from outside the predicted distribution were added. For this, a binary grid mask based on the species distribution model (SDM) was generated, which included habitat suitability values above a minimal threshold of 0.2 (based on multiple cross-validation evaluations, see Species distribution model below). To exclude internal areas with low suitability scores, the raster was converted to polygons (rasterToPolygons) and we used only the polygon with the largest area (electronic Supplementary data S3). Random coordinates of cells outside this polygon were sampled and assumed to have an ancestry coefficient of zero for all groups. Once Kriging models were generated for each group, the interpolate function (bilinear method) from the package raster46 was used to extrapolate ancestry coefficients to the whole surface. Finally, all cells that had ancestry coefficients below the 80% quantile were ignored. This approach was similar (i.e., same under-the-hood functions) to the package tess3r47.
Species distribution model
The distribution of G. agassizii was reconstructed based on 11 environmental variables that were proposed previously to represent desert tortoise distribution19. These variables encompassed topography (elevation and slope), climate (precipitation and temperature), soil (depth to bedrock, fine earth density, coarse fragment volume) and vegetation (vegetation coverage) (Table 1). A detailed variable explanation and plausible connections to tortoise biology and ecology were supplied as electronic Supplementary file S2. All grid/raster data were downloaded at a resolution equal to or higher than 0.01 degrees or 1,000 × 1,000 meters. Raster files with higher resolution were downscaled to 0.01 degrees in R, using the aggregate and resample functions from the package raster. All layers were adjusted to the same coordinate projection system (EPSG: 4326 or +proj = longlat + ellps = WGS84 + datum = WGS84 + no_defs) and cropped to an extent delimited by longitude: −120, −112, and latitude: 32, 38.
Presence data consisted of 1,848 downloaded georeferenced records of G. agassizii from the Global Biodiversity Information Facility (GBIF) server within the area of study. After adding our own georeferenced data, 2,565 presence coordinates were obtained. To avoid data redundancy and same-cell overrepresentation, our presence data were reduced to 645 coordinates representing cells with presence data only (600 × 800 matrix). To generate pseudo-absence data, 10,000 random coordinate points were simulated and cells (1000 × 1000 m) were selected based on those points. Cells with presence data were excluded from the absence data set.
MaxEnt48 was employed to model habitat suitability based on the environmental data as predictor variables, and presence and pseudo-absence coordinate data. MaxEnt, which is a statistical machine-learning model based on the principle of maximum entropy, has been used often for predicting distributions of species49. The model was evaluated using a 10-fold cross-validation approach where all the data were separated into small training and testing sets. All statistical evaluation parameters, such as the area-under-the-receiver-operating-characteristic curve (AUC), were summarized across replicates. Variable importance was determined using a jackknife approach. Threshold values were estimated for each replicate and averaged. Habitat suitability scores were inferred using the predict function of the package raster. Because G. agassizii mostly occurs west and north of the Colorado River, we excluded suitability scores east of the Colorado River in the SDM (see electronic Supplementary file S3).
Geographic- and landscape-based distance matrices
An individual-based approach was used to test for IBD, IBE and IBR. First, genetic distances were estimated with the function dist_amova using multivariate genotypic data in the R package gstudio50. These distances were equivalent to the sum of the squared Euclidean distance between the ith and the jth genotype51,52. Next, matrices with Euclidean geographic and environmental distances were constructed, as well as landscape resistance distances either based on LCD or RD18. To have a single individual per cell, one individual was randomly selected in cases where more than one individual was found per cell. Samples from the Upper Virgin River recovery unit (electronic Supplementary file S3) were excluded due to the sampling gap between California and Utah. After this reduction, data for 277 individuals were analyzed. All raster and spatial objects were transformed to Universal Transverse Mercator (UTM) units either using the projectRaster or the spTransform functions from the R packages raster and sp. The spatial resolution of all raster grids was 1000 × 1000 m. Euclidean distances were calculated using the R function dist, and given that UTM units were meters, Euclidean distances were scaled to km. Data from all environmental layers (Table 1) were proportionally rescaled to fit values between 1 and 10. For environmental distances, we extracted environmental values for subsampled individuals with genetic data (n = 277) and for all rasters. Then, we calculated Euclidean environmental distances between individuals.
Expert opinion has been the most common way to empirically assign resistance values. Analytical approaches that involve applying parametric statistical models based on individual distributions have been shown often to be more flexible, informative, and pragmatic53. Therefore, we assigned resistance values analytically. First, we extracted the values of cells with presence data (n = 1,848) and calculated the density distribution (density) for each variable. Then, we fitted cubic smoothing splines (smooth.spline) with the values of the density distribution as the response variable and the sampled environmental values from the distribution as predictor variables. We used this model to extrapolate density values to all data cells for each raster. Resistance was assumed to be 1–density to assign lower values to cells with higher density or less friction. The cell values in all rasters were again rescaled [1, 10]. We did this for all environmental variables except for the SDM, where direct habitat suitability (1–suitability score) was taken as a proxy for resistance; low suitability scores equaled higher resistance. Similarly, slope was evaluated by using both the degree of the slope as a measure of friction and by using the density approach described above. To improve computational efficiency, all 12 layers were trimmed to a polygon defined by the convex Hull of the largest polygon in the SDM (electronic Supplementary file S3).
LCD was calculated using the function costDistance, which is based on Dijkstra’s algorithm, in the R package gdistance54. First, a conductance transition object was generated on all layers, considering the eight immediate neighboring cells. Because gdistance required transition objects for conductance, rather than resistance values, the function 1/mean(resistance) was used to obtain a conductance matrix. An R script (https://github.com/santiagosnchez/runCS) that ran CircuitScape55 in the background was used to calculate RD, directly loading matrices as dist objects in R. Least-cost distance and resistance distance matrices were linearized as vectors and stored as data frames.
Statistical analyses
Following Shirk et al.23, two approaches for model evaluation were used. The first approach used linear mixed-effect modeling with MLPE24. Models were fitted using the function MLPE.lmm in the R package ResistanceGA56. Population assignments (K = 5) for every pair of individuals or every distance value in the matrix were used to build the correlation structure. This information was specified as a sparse matrix, which was built using a matrix with two columns and n(n−1)/2 rows (n is the number of individuals), to the ZZ argument in the MLPE.lmm function. The model considered the relationships between genetic distances and the predictor distances as fixed effects, and the population structure relationships as random effects. Univariate models were compared using the Akaike Information Criterion (AIC)23,57 and Bayesian Information Criterion (BIC) with maximum likelihood, not restricted maximum likelihood (REML), as REML has caused issues in mixed-effect model comparisons58. MLPE.lmm used the lme459 package internally.
The second approach applied reciprocal causal modeling (RCM) with partial Mantel tests16,25. The mantel function in the ecodist package60 was used to perform partial Mantel tests for each pair of variables. In every case, the Rm (Mantel’s R) was calculated using 999 permutations having one of the variables as the main variable and suppressing the alternative variable (model A). The reciprocal test (model B) was performed next. If the difference in Rm between model A and model B was positive, then the test favored model A, and if it was negative or zero it favored model B61. As in Ruiz-Gonzalez et al.61, RmA−RmB, results were reported in a colored heat map where red colors indicated negative values and blue colors indicated positive values. RmA−RmB values were summed for each column to simplify variable ranking. The heat map was plotted using the R package plotly.
Outlier loci detection analysis
BayeScan v2.162 was used to detect outlier loci (n = 646, loci = 6,859). This used a Bayesian multinomial Dirichlet model to estimate allele frequencies and FST coefficients, which were then decomposed into population-specific (beta) and locus-specific (alpha) components. Loci for which the locus-specific component was necessary to explain the observed variation were considered non-neutral (e.g., alpha significantly different than 0). Positive alpha values indicated that the locus was under positive diversifying selection, while negative values indicated negative purifying selection. A reversible-jump Monte Carlo Markov chain was then used to select one of two models, in which the alpha component was added or not. Before running the program, a VCF file was converted to the input format required by BayeScan for SNP data (https://github.com/santiagosnchez/vcf2bayescan). Next, BayeScan was run with default MCMC settings (-n 5000 -thin 10 -nbp 20 -pilot 5000 -burn 50000), except for the posterior odds prior (pr_odds), which was set to 100. Increasing the posterior odds prior increased the sensitivity and made the analysis more conservative, particularly because more than 1,000 markers were analyzed. Outlier loci were detected by plotting the FST coefficients against the log10 of the posterior odds, and the q-values (false discovery rate analog of p-value) against alpha. Thresholds were marked by 2 (log10(100)) on the x-axis, and q-value of 0.05 on the y-axis, for each case. The closest function in bedtools v2.2663 was used to find the closest annotated gene for each outlier locus.
The distribution of the minor allele (lowest frequency allele) of outlier loci was modeled in a similar way as in the spatial ancestry interpolation. A VCF file with outlier SNPs was imported into R using read.vcf from the package pegas64. Then each locus was converted to a numeric multivariate format in which both alleles were separated into homozygotes (1 or 0) and heterozygotes (0.5). The spatial analysis was done as described earlier using Krig interpolation. This analysis was only performed on loci that were close to annotated genes to facilitate physiological interpretation in a spatial context.
Data availability
Sequencing data were deposited in NCBI under the BioProject ID PRJNA450441. Scripts used for bioinformatics were made available through GitHub (https://github.com/santiagosnchez). All other data were supplied as online supplementary files.
Results
Sequence and SNP data
An average of 930,203 reads (SD = 1,335,739, min = 3,098, max = 15,846,603, n = 1032) were generated per individual after quality control filtering. From these, an average of 906,208 reads were successfully mapped to the reference genome. Read depth averaged 13.6 across all samples (SD = 16.8, max = 1049.7). The average number of scored loci was 54,152 (SD = 47,805.54, min = 5,014, max = 342,811, n = 845) per sample after excluding samples with less than 5,000 scored loci. Due to poor data-yield, 386 samples were excluded (good quality, n = 646 after exclusion). We catalogued 1,046,121 loci, most of which were excluded for not being present in at least 50% of all samples. Ultimately, after filtering out low quality data, 6,859 SNPs were retained for analyses.
Genetic structure
A group size of 5 clusters (K = 5) had the lowest cross-validation error (CVE = 0.42897), followed closely by K = 4 clusters (CVE = 0.42979; Fig. 2A,B). K values ranging from 3 to 9 had marginally worse errors (Fig. 2A,B). For K = 5, groups included the following proposed recovery units based on Murphy et al.9: Cluster 1 (purple) represented the central Mojave group; Cluster 2 (blue) the western Mojave group; Cluster 3 (green) the southern Mojave group; Cluster 4 (yellow) included the Eastern Colorado, Eastern Mojave, and Northern Colorado recovery units; Cluster 5 (red) included Northeastern Mojave and Upper Virgin River recovery units (Fig. 2B). For K = 5, pairwise FST values ranged between 0.209 (between Cluster 1 and 2) and 0.283 (between Cluster 3 and 5). Recovery units that were recognized with other K values included Northeastern Mojave and Upper Virgin River groups (K = 6 and K = 7) and the Eastern Colorado (K = 8) (Fig. 2B). Eastern Mojave and Northern Colorado appeared as a single cluster at K = 8 (Fig. 2B). In addition, the population at Daggett, found between the southern, western, and central Mojave groups, was resolved as a distinct group at K = 7 and K = 8 (Fig. 2B). The DAPC (Fig. 2C) was mostly congruent with the structure found by Admixture, as we also found 5 groups. The group representing the most variation in PC1 and the most genetically distant was Cluster 5 (Fig. 2C). Clusters 1–4 differentiated from each other along PC2, with Cluster 4 being the most distinct among them. The most genetically heterogeneous group, with ordination values more centrally distributed, was the southern Mojave (Cluster 3; Fig. 2C). The DAPC based on the K = 5 clusters retained the first 30 PCs and three discriminant functions, while the one based on the populations from Murphy et al.9 retained the first 60 PCs and seven discriminant functions.
Analysis of genetic structure in Agassiz’s desert tortoise (Gopherus agassizii). (A) Bootstrapped (n = 10) 5-fold cross-validation error estimations for clusters form K = 1 to K = 10. The best K value is marked with the vertical dashed line. Statistically significant differences were found between the best K, and the second and third best K values, respectively (Wilcoxon rank sum test: W = 91.5, p-value = 0.002 [***]; W = 82,5, p-value = 0.01 [**]). (B) Bar plot with ancestry proportions per individual for 4 to 8 clusters. (C) Genetic ordination analysis using the population structure inferred by Admixture (K = 5) and that from Murphy et al.9 central Mojave (n = 81), western Mojave (n = 71), southern Mojave (n = 374), Eastern Colorado (n = 31), Eastern Mojave (n = 17), Northern Colorado (n = 10), Northeastern Mojave (n = 30), Upper Virgin River (n = 32).
Species distribution modeling
An average AUC of 0.875 (SD ± 0.021) from 10 cross-validation runs indicated a good model fit and a significant deviation from random or homogeneous prediction (i.e., AUC close to 0.5). Based on Jackknife and permutation analyses, the variable depth-to-bedrock (soil) had the largest contribution to the model (average = 42.3%), followed by elevation (topography; average = 15.7%), and mean temperature during the wet season (climate; bio8, average = 13.6%). All other variables contributed from 7 to 1%, with the lowest being coarse fragment volume (soil, Table 1). Visually, the predicted SDM coincided with the Mojave and Colorado deserts. A map of the SDM excluding areas south and east of the Colorado River, and areas with habitat suitability <0.2, was supplied in electronic Supplementary file S3.
Spatial and landscape genetics
By interpolating the ancestry coefficients, 5 spatially well-defined clusters were identified (Fig. 3F). Most of Cluster 1 was confined to the north-central part of the populations in California (Fig. 3A). Cluster 2 included the far western portion of geographic range (Fig. 3B). Cluster 3 was largely confined to the south-central portion of the Mojave Desert with some presence of admixed individuals (Fig. 3C). Cluster 4 dominated the eastern and southern portions of California, in the eastern and northern Colorado Desert and eastern Mojave Desert (Fig. 3D). Cluster 5 (Northeastern Mojave, Upper Virgin River) stretched from the northeastern portion of the geographic range in California, into Nevada and the southwestern corner of Utah (Fig. 3E).
Spatial interpolation of ancestry coefficients of Agassiz’s desert tortoises (Gopherus agassizii) using Krig modeling, superimposed on a shaded relief (made with Natural Earth. Free vector and raster map data@http://www.naturalearthdata.com/downloads/10m-raster-data/10m-manual-shaded-relief/). (A) Cluster 1; (B) Cluster 2; (C) Cluster 3; (D) Cluster 4; (E) Cluster 5. The last map (F) combines areas of maximal ancestry proportion for each of the five genetic groups. In F, the total area was trimmed using the species distribution model (darker grey area). Contour lines indicate 0.1–0.9 quantiles. The scale bar in the smaller map in E is equivalent to 500 km. The points highlighted in the white, transparent circle indicate to the population at Daggett. Maps were generated with the R package raster v2.6 (https://cran.r-project.org/web/packages/raster/index.html).
Both landscape genetic approaches were consistent with each other for the best selected landscape factors. For MLPE, the best model resulted in the mixed-effect linear correlation of genetic distance and LCD based on elevation, followed by average winter precipitation (bio16), habitat suitability (SDM), and depth-to-bedrock (d2b) (Table 2). These variables were better predictors of genetic distance than Euclidean geographic distances (geo) or IBD (Table 2). Similarly, LCD based on variables such as slope (based on slopeD), vegetation coverage (vegS, vegW), the volume of coarse soil fragments (cfv), and the average summer precipitation (bio9) were also better predictors of genetic distance than the null, geographic distance model. In contrast, only one RD variable (summer vegetation coverage) was better than the null model. RCM with partial Mantel tests showed similar results. Six LCD variables (elev, bio16, SDM, bio9, d2b, vegS) had overall better support than the null model (Fig. 4A). RCM did not show strong support for RD models when compared to geographic distances (Fig. 4B). With respect to IBE, none of the environmental distance matrices were better predictors of genetic distance than the IBD or IBR models (Table 2, Fig. 4C). MLPE and RCM differed mainly in the number and relative importance of the best supported predictor variables.
Pairwise heatmaps with reciprocal causal modelling results showing RmA − RmB for (A) least-cost distance models, (B) resistance-distance models, and (C) environmental distance models. Columns represent the main variables and rows represent the alternative variables. Thus, the figure should be read by columns and not by rows. For each column, blue squares indicate a supported variable against an alternative variable. Red squares indicate support for the alternative variable (degree indicated by scale on the right). On top of each heatmap the RmA−RmB value is summed for the null model (geographic distance), marked by a white box, and the testing variables marked by a grey box. Variables that were better supported than the null model are also marked with an asterisk.
Loci under selection
Convergence of the MCMC chain in BayeScan was assured by plotting the log-likelihood against generations. The prior odds value of 100 was used to select loci with log10(PO) > 2, which resulted in loci emitting a very strong to decisive signature (q-value > 0.99). This identified 32 outlier loci (Fig. 5A). Eighty-one outlier loci (Fig. 5B) were detected by choosing a q-value threshold of 0.05. Given that the first threshold was more conservative, and that the first 32 loci were included in the later 81, we only report the former BayeScan results and their closest genes with annotation (if any) in Table 3. From the 32 loci, 21 were on scaffolds with no annotations, 10 were close to an annotated gene of known function, two were close to an annotated gene of unknown function, and the SNP position of five loci occurred within the gene (Table 3). The five SNPs that were found within genes were in introns. The farthest distance from the nearest annotated gene was 67 kbp.
BayeScan outlier loci detection using a log10 posterior odds threshold of 100 (left) and a false discovery rate (FDR) threshold of 0.05 (right). Values at 1000 log10 posterior odds in the left panel should be infinity because the probability was estimated to be 1; however, BayeScan automatically fixes the log10(PO) to 1000 in these cases. All black-colored loci had a probability ≥ 0.99.
The distributions of the minor alleles of outlier loci that were on or close to annotated genes were modeled (Fig. 6). Overall, the distributions of some loci were fairly population-specific (e.g., 3264_0, 11119_0 and 15060_0 in Fig. 6). Other alleles were found mostly among northern populations (e.g., 2293_0, 2747_0, 4574_0, 5683_0, 15846_0 in Fig. 6), or, to some extent, were rather widespread (e.g. 7003_0 and 15920_0 in Fig. 6).
Spatial modelling of outlier minor alleles on or close to an annotated gene. See Table 3 for reference. Raster data is superimposed on a shaded relief (made with Natural Earth. Free vector and raster map data @ http://www.naturalearthdata.com/downloads/10m-raster-data/10m-manual-shaded-relief/). Maps were generated with the R package raster v2.6 (https://cran.r-project.org/web/packages/raster/index.html).
Discussion
A major goal in conservation genetics involves performing spatial and genetic assessments of evolutionary significant units to gain knowledge about factors influencing population structure2,65,66. The extent to which the landscape limits genetic connectivity may potentially inform about the species potential for dispersal and interactions with the environment67. Analyses of vast genotypic data (more than 6,000 SNPs), ample sampling throughout the Mojave and Colorado deserts68, and high-resolution GIS data enable powerful insights about the spatial features and genomic composition of desert tortoise populations. The type and volume of data offer unprecedented value for desert tortoise conservation, making possible a more accurate assignment of individuals to spatially defined genetic units, measurement of intra- and inter-population relationships, and allowing for identification of candidate genes on which natural selection may be ocurring27,28.
Species distribution modelling
Species distribution models are an important tool for modern spatial analyses in conservation, and other biological applications69. Our SDM constitutes ‘proof-of-concept’ by enhancing multiple analyses. For instance, it improves our spatial ancestry prediction (Fig. 3) where we characterize the absence of genetic data outside a probable distribution margin. We also use the SDM to remove ancestry predicted outside the species’ known range (electronic Supplementary file S3), visually resolving landscape features (e.g. mountains and deep valleys) that may influence spatial genetic structure (Fig. 3F); this step can help us identify likely contact zones between genetic groups. Lastly, we incorporate and test the SDM as a source of heterogeneity in our landscape genetic analyses, as others have done13, finding that individual variables can be more informative in explaining genetic connectivity than only using habitat suitability scores.
Genetic structure
Our analyses detect from four to seven genetically distinct groups (Fig. 2) with well-defined spatial boundaries (Fig. 3) that coincide well with existing and proposed recovery units9,10,12. For example, Clusters 1, 2 and 3 (K = 5) essentially correspond to the central, western, and southern Mojave populations proposed as recovery units in Murphy et al.9. Some agreement also occurs with respect to the Eastern Colorado, Northeastern Mojave, and Upper Virgin River populations at K = 6 and K = 8. To a large extent, our second DAPC analysis (Fig. 1C), based on the populations delimited in Murphy et al.9, mirrors their 2-dimensional scaling plot using FST distances between sampled locations (Fig. 5 in Murphy et al.9). The high resemblance in results might be partially due to the re-analysis of many of the same samples, albeit using considerably more, new and different data. Analyses of these data show strong genetic relationships within the southeastern (Eastern Mojave, Eastern Colorado, and Northern Colorado), western (western, central, and southern Mojave), and northeastern (Northeastern Mojave and Upper Virgin River) groups.
Our genome-level analyses, together with the results in Murphy et al.9, support the hypothesis that the Western Mojave recovery unit, as proposed originally in the Desert Tortoise Recovery Plan12, is a conglomerate of at least three distinct genetic groups. Our results contrast with the study of Hagerty and Tracy10, which supports the Western Mojave recovery unit as a single group. In support of our hypothesis, the genetic distinctiveness of these three groups remains consistent at K values ranging from 4 to 8 (Fig. 1B), and in the DAPC analysis (Fig. 1C). Other than this disagreement, our analyses are consistent with the Eastern Colorado and Northern Colorado groups described by Hagerty and Tracy10. To some extent, our analyses also correspond to their groupings in Nevada and Utah (specifically Southern Las Vegas and Virgin River), which match our Northeastern Mojave and Upper Virgin River groups, respectively. Differences in sampling may account for discordance between our results and Murphy et al.‘s compared to Hagerty and Tracy’s. For instance, using stronger sampling in Nevada and Utah, Hagerty and Tracy resolved a higher level of structure than we resolve. In contrast, our study has stronger sampling in the western portion of the Mojave Desert, where we find a higher level of genetic subdivision. Recent genetic simulations on IBD models69 demonstrate that population-level sampling (e.g.9 and this study) may better resolve membership identification than does random sampling (e.g.10) in a IBD scenario. However, we suggest that for conservation purposes all information available should be synthetized into a single framework.
Although we do not quantify gene flow directly, and drift can also be an important factor leading to divergence, both structure and landscape genetics analyses (next section) suggest admixture patterns between the different groups. The southern Mojave population (Cluster 3) seems to be the most admixed group (Fig. 1B,C). Clusters with genetic contributions mainly include geographically contiguous populations, such as those in the western and central Mojave to the west and north, respectively, as well as the Eastern Colorado in the south. Admixture appears to occur between the central Mojave and western Mojave populations, which are close to one another (Figs 2 and 3). While few barriers exist (i.e., Black Mountain in Fig. 1) between these populations, environmental differences are more notorious9. Tortoises in the eastern and southern recovery units (Eastern Mojave, Eastern Colorado, and Northern Colorado; as described in12; Fig. 1) appear to be more admixed with populations in the southern, central and western Mojave than with populations in the Northeastern Mojave and Upper Virgin River recovery units (Figs 2 and 3). Admixture between the central Mojave group and populations further east may be limited by the Avawatz, Soda, Clark and Mesquite mountains. Similarly, the Northeastern Mojave recovery unit and populations to the south in the East Mojave and Colorado Desert recovery units may be limited by the Providence, New York, Piute and El Dorado mountains in northeastern California and southern Nevada (Fig. 1). Despite the close geographical distance of our samples in the Northeastern Mojave recovery unit to other Californian groups (Fig. 1), this population still has a higher genetic affinity with the more distant Upper Virgin River recovery unit (Fig. 2C,B). This genetic affinity between both groups occurs even in spite of the sampling gap in Nevada, which should result in structured populations29.
The extent and directionality of admixture, together with the spatially explicit genetic structure (Figs 2 and 3), suggest a pattern recognizable as IBD. Five previous studies have described IBD as a likely evolutionary force driving population structure in desert tortoises8,9,10,13,14. As the authors suggested, limited dispersal, previous and present barriers, and climatic features are thought to be important factors effecting genetic differentiation3,9,71,72,73,74.
Landscape effects on genetic connectivity
The effects of IBD are usually assessed by inspecting relationships between Euclidean (e.g., straight line) inter-individual or inter-population geographic distances and genetic distances15. In contrast, more sophisticated landscape genetic approaches1 apply IBR models to evaluate the effect of landscape heterogeneity on genetic connectivity16,18. Because IBD can conflate IBR, our assessment uses multiple IBE models in a comparative framework. Our results do not find a direct influence of raw environmental distances on population structure. In contrast, IBD and IBR models are consistently better supported than IBE, suggesting that spatial features may be more important than raw environmental differences. Moreover, analyses find that several landscape features are better predictors of genetic connectivity than geographic distances (Table 2, Fig. 4A). Some of these features also may seem to be relevant for niche partitioning between G. agassizii and G. morafkai, which are genetically close and geographically adjacent species74.
Elevation is the best supported variable by both MLPE and RCM, and also contributes significantly to the SDM model. Previous microsatellite-based landscape genetic analyses have concluded that topological features restrict gene flow in desert tortoises13,14. Hagerty et al.13 reported that mountains and deep valleys serve to limit gene flow, albeit with marginal support. This reinforces field observations and distribution models suggesting that tortoises generally avoid steep slopes, high elevation areas, and playas12,19,75. Typical desert tortoise habitat can range from sandy plains to rocky or rolling foothills, including alluvial fans, washes, and canyons12. Tortoises also spend most of the year underground76, which means that they are likely to be found in areas with soils suitable for burrowing or caves in well-developed calcic layers77,78. This makes the idea of testing soil variables appealing. In fact, our analyses find support for variables such as the absolute depth-to-bedrock and fraction of coarse (>2 mm) soil fragments (Table 2, Fig. 4A), which might be relevant to burrowing. Depth-to-bedrock also has the highest contribution to the SDM, even more so than elevation, indicating that it is a relevant landscape feature for predicting tortoise habitat78.
Rainfall has strong effects on food plant production79,80,81 and provides drinking water essential for life35,76,82. Better nutrition and access to water can, in turn, improve health, and increase growth, activity, and reproductive output35,37,76,82,83,84,85. Rainfall also stimulates growth of plants (e.g., shrubs and other perennials) that provide tortoises shade and shelter, plus stability to soils that support tortoise burrows. Interestingly, our analyses find average winter precipitation and vegetation coverage (winter and summer) to be good predictors of genetic connectivity (Table 2, Fig. 4A). Because tortoises can find suitable habitat conditions at a fine scale86, both the scale of the study (1000 × 1000 m) and/or the high variability of the landscape due to low primary productivity of deserts, could have hindered the relationship between vegetation coverage and genetic connectivity. However, our results show that even at broader scales the amount of vegetated land, in particular perennial plants, can have a substantial impact on how desert tortoise populations are structured.
Circuit-based IBR models were introduced as more realistic alternatives to LCP analyses, which assume that individuals have preferred dispersal routes1,16,18. In contrast, RD is quantified as the average random walks between locations, assuming that gene flow happens through multiple, alternate routes18,56. LCD models for the best variables (Table 2, Fig. 4) are better predictors of genetic distance, which implies that genetic corridors among tortoises tend not to follow random routes. Instead, corridors may follow narrower paths that are optimal for them to increase their movement efficiency. Noteworthy, in nature, tortoises have high site fidelity, and tend not to move far away from burrows, rock shelters and dens. Tortoises are aware of geophagy sites87,88, drinking basins82 and other resources (e.g., conspecifics) in their home ranges. Thus, because genetic variation accumulates over time, it is important to frame genetic connectivity as a measure that represents evolutionary tendencies of genetic exchange, and not as a measure that represents contemporary movement.
Management perspective
Understanding the genetic units of tortoises is important for managing this threatened species. Genetic units, among other factors, form the basis of recovery units for the Mojave population of desert tortoises12. It is possible to improve management techniques, including population augmentation (e.g., headstarting and translocation), by incorporating knowledge of genetic boundaries and distances that tortoises should be moved. Our analyses delineate genetic population boundaries by using robust sampling for most of the species’ geographic range. These genetic boundaries are similar but not identical to those proposed by Murphy et al.9 and Hagerty and Tracy10.
Averill-Murray and Hagerty89, using genetic boundaries drawn by Hagerty and Tracy10, wrote that populations “within a 200–276 km straight-line radius of each other (249–308 km measured around topographic barriers) tend to be genetically correlated and may be considered single genetic units for management purposes.”. Our findings, drawing on more robust genetic analyses, indicate the prudence of considering the importance of population boundaries in addition to distance. Distances of 200 km extend across several genetically identifiable populations (i.e., western Mojave, central Mojave, Daggett, and the southern Mojave) in the Western Mojave recovery unit, and across genetically identifiable populations in the southern Mojave to the eastern Colorado Desert. Mixing genetic populations could lead to outbreeding depression, failure to integrate, thrive, and survive9,90,91, or outbreeding vigor90, although there are no ‘common garden’ studies92,93 or other empirical investigations that explore these phenomena for G. agassizii. Via conservative management, however, we may limit risks by avoiding population augmentations across genetic population boundaries or over long distances94. Consistent with this approach, headstart tortoises in the western, central, southern, and northeastern Mojave genetic populations are being placed within their genetic population of origin.
Loci under selection and their functions
Our analyses consider outlier loci for two reasons. First, we confirm that the majority (99.5%) of loci are neutral, which is an assumption in models of population structure95. Second, the approach can identify genes or neighboring genes of loci that strongly conform to a non-neutral model26. In a recent conservation genomics study of the Burmese roofed turtle (Batagur trivittata), from about 1500 SNPs, not a single locus departed significantly from neutrality96. In contrast, our analyses discover at least 32 loci under potential diversifying selection. Among 12 loci that associate with annotations, five variants occur within introns of five genes (Table 3), upon which the effects of selection are likely to be stronger due to linkage97,98, if, in fact, these genes are targets of selection. Analyzing RNA expression of these candidate genes can help understand their fitness effects. Likewise, dN/dS-type analyses of sequence data for the whole gene and multiple species can also provide additional evidence for selection.
Some genes in the vicinity of these loci have functions that may be involved with neurogenesis, wound healing, lipid metabolism and vitellogenesis. More specifically, noteworthy functions include the following: Beta-thymosin (IPR001152), a multi-function protein involved with cellular processes such as wound healing, actin formation (muscle development), embryonic organ development, and disease pathogenesis99,100; ADAM9 (IPR006586), a membrane-anchored protein involved with cell adhesion, fertilization, muscular development and neurogenesis101; Roundabout homolog 2 (IPR032985) and SCO-spondin (IPR030119), which are independently related to axonal migration, growth, neural development, and tissue development102; and cholesteryl ester transfer protein (IPR017130), with functions related to lipid and cholesterol control103.
The direct relationship between allele frequencies, gene functions, and their implication on the biology of tortoises is difficult to assess. However, the cholesteryl ester transfer protein (IPR017130) might point to interesting future research given the association of lipid metabolism with energy storage and vitellogenesis among desert tortoises37,85. Lipid metabolism helps females increase body lipid reserves they use subsequently during periods of low resource availability, such as drought and brumation, and stimulates egg production85. Cholesterol and triglyceride levels have been found to vary between females and males, and among seasons, where they are high in spring when females are preparing eggs37. Egg production among female desert tortoises varies with the amount of rainfall or concomitant primary production81,104 and distribution (i.e., East-to-West Mojave108). However, our results show that the minor allele associated with the cholesteryl ester transfer protein occurs mostly in northern areas (Fig. 6: 2293_0) and has no east-to-west variation. Moreover, this protein may serve other functions. For instance, a variant of the cholesteryl ester transfer protein in humans has been linked to larger high- and low-density lipoprotein particle sizes, which may decrease hypertension and cardiovascular disease, therein promoting longevity105. A recent comparative genomic analysis in chelonians has revealed several genes involved with longevity and fatty acid metabolism to be under a high rate of molecular evolution31.
Conclusions
Landscape genomics aims at identifying complex interactions between the environment and the genome of individuals in a population. These interactions include, but are not limited, to how the landscape limits gene flow between and within populations, and how genome-wide allele frequencies change as a function of space and the environment. With better inferences about these interactions and underling biological processes, better conservation and wildlife management actions can take place to restore major, threatened species, such as the desert tortoise. For the first time, we generate thousands of genome-wide genotypic data for hundreds of individuals in desert tortoises, which have helped to robustly assess the population structure in the species. By coupling genetic and spatial interpolation techniques, analyses delimit genetic clusters spatially, which can help inform potential locations for translocation and headstart releases, and where interpopulation interactions may occur. We also apply novel statistical methods to evaluate the effect of the landscape on genetic connectivity, using geographical distance as a null model. Our results allow us to build on previous studies, showing how several environmental, climatic, and biotic features explain genetic differences between populations. Finally, we identify potentially non-neutral loci that are in the vicinity of genes that may be involved with neurogenesis, wound healing, lipid metabolism and vitellogenesis. While their direct correlation to the environment is still uncertain, this research opens new directions for conservation genomics in desert tortoises.
References
Manel, S., Schwartz, M. K., Luikart, G. & Taberlet, P. Landscape genetics: combining landscape ecology and population genetics. Trends Ecol. Evol. 18, 189–197 (2003).
Manel, S., Gaggiotti, O. E. & Waples, R. S. Assignment methods: matching biological questions with appropriate techniques. Trends Ecol. Evol. 20, 136–142 (2005).
Bender, G. L. Reference Handbook on the Deserts of North America (Greenwood Press, 1982).
Berry, K. H., Morafka, D. J. & Murphy, R. W. Defining the desert tortoise (s): our first priority for a coherent conservation strategy. Chelonian Conserv. Biol. 4, 249–262 (2002).
Lamb, T., Avise, J. C. & Gibbons, J. W. Phylogeographic patterns in mitochondrial DNA of the desert tortoise (Xerobates agassizi), and evolutionary relationships among the North American gopher tortoises. Evolution 43, 76–87 (1989).
Rainboth, W. J., Buth, D. G. & Turner, F. B. Allozyme variation in Mojave populations of the desert tortoise. Gopherus agassizi. Copeia 1989, 115–123 (1989).
Edwards, T. Desert tortoise conservation genetics. (University of Arizona, 2003).
Edwards, T., Schwalbe, C. R., Swann, D. E. & Goldberg, C. S. Implications of anthropogenic landscape change on inter-population movements of the desert tortoise (Gopherus agassizii). Conserv. Genet. 5, 485–499 (2004).
Murphy, R. W., Berry, K. H., Edwards, T. & McLuckie, A. M. A genetic assessment of the recovery units for the Mojave population of the desert tortoise. Gopherus agassizii. Chelonian Conserv. Biol. 6, 229–251 (2007).
Hagerty, B. E. & Tracy, C. R. Defining population structure for the Mojave Desert tortoise. Conserv. Genet. 11, 1795–1807 (2010).
U.S. Fish Wildlife Service. Endangered and threatened wildlife and plants; determination of threatened status for the Mojave population of desert tortoise (U.S. Fish Wildlife Service, 1990).
U.S. Fish Wildlife Service. Desert tortoise (Mojave population) recovery plan (U.S. Fish and Wildlife Service, 1994).
Hagerty, B. E., Nussear, K. E., Esque, T. C. & Tracy, C. R. Making molehills out of mountains: landscape genetics of the Mojave Desert tortoise. Landsc. Ecol. 26, 267–280 (2010).
Latch, E. K., Boarman, W. I., Walde, A. & Fleischer, R. C. Fine-scale analysis reveals cryptic landscape genetic structure in desert tortoises. PLoS One, 6, e27794–10 (2011).
Rousset, F. Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics 145, 1219–1228 (1997).
Cushman, S. A., McKelvey, K. S., Hayden, J. & Schwartz, M. K. Gene flow in complex landscapes: testing multiple hypotheses with causal modeling. Am. Nat. 168, 486–499 (2006).
Wang, I. J. & Bradburd, G. S. Isolation by environment. Mol. Ecol. 23, 5649–5662 (2014).
McRae, B. H. Isolation by resistance. Evolution 60, 1551–1561 (2006).
Nussear, K. E. et al. Modeling habitat of the desert tortoise (Gopherus agassizii) in the Mojave and parts of the Sonoran Deserts of California, Nevada, Utah, and Arizona (U.S. Geological Survey, 2009).
Guillot, G. & Rousset, F. Dismantling the Mantel tests. Methods Ecol. Evol. 4, 336–344 (2013).
Zeller, K. A. et al. Using simulations to evaluate Mantel-based methods for assessing landscape resistance to gene flow. Ecol. Evol. 6, 4115–4128 (2016).
Legendre, P., Fortin, M.-J. & Borcard, D. Should the Mantel test be used in spatial analysis? Methods Ecol. Evol. 6, 1239–1247 (2015).
Shirk, A. J., Landguth, E. L. & Cushman, S. A. A comparison of regression methods for model selection in individual-based landscape genetic analysis. Mol. Ecol. Res. 32, 267–13 (2017).
Clarke, R. T., Rothery, P. & Raybould, A. F. Confidence limits for regression relationships between distance matrices: Estimating gene flow with distance. J. Agr. Biol. Envir. St. 7, 361–372 (2002).
Cushman, S., Wasserman, T., Landguth, E. & Shirk, A. Re-Evaluating causal modeling with Mantel tests in landscape genetics. Diversity 5, 51–72 (2013).
Morin, P. A., Luikart, G. & Wayne, R. K. The SNP workshop group. SNPs in ecology, evolution and conservation. Trends Ecol. Evol. 19, 208–216 (2004).
Allendorf, F. W., Hohenlohe, P. A. & Luikart, G. Genomics and the future of conservation genetics. Nat. Rev. Genet. 11, 697–709 (2010).
Shafer, A. B. A. et al. Genomics and the challenging translation into conservation practice. Trends Ecol. Evol. 30, 78–87 (2015).
Schwartz, M. K., McKelvey, K. S., Cushman, S. A. & Luikart, G. Landscape genomics: a brief perspective in Spatial Complexity, Informatics, and Wildlife Conservation (Eds. S. A. Cushman & F. Huettmann) 165–174 (Springer, 2010).
Bragg, J. G., Supple, M. A., Andrew, R. L. & Borevitz, J. O. Genomic variation across landscapes: insights and applications. New Phytol. 207, 953–967 (2015).
Tollis, M. et al. The Agassiz’s desert tortoise genome provides a resource for the conservation of a threatened species. PLoS One 12, e0177708–26 (2017).
Peterson, B. K., Weber, J. N., Kay, E. H., Fisher, H. S. & Hoekstra, H. E. Double digest RADseq: an inexpensive method for de novo SNP discovery and genotyping in model and non-model species. PLoS One 7, e37135–11 (2012).
Andrews, K. R., Good, J. M., Miller, M. R., Luikart, G. & Hohenlohe, P. A. Harnessing the power of RADseq for ecological and evolutionary genomics. Nat. Rev. Genet. 17, 81–92 (2016).
U.S. Fish and Wildlife Service. Desert Tortoise Monitoring Handbook (U.S. Fish and Wildlife Service, 2015).
Henen, B. T., Peterson, C. D., Wallis, I. R., Berry, K. H. & Nagy, K. A. Effects of climatic variation on field metabolism and water relations of desert tortoises. Oecologia 117, 365–373 (1998).
Christopher, M. M., Berry, K. H., Henen, B. T. & Nagy, K. A. Clinical disease and laboratory abnormalities in free-ranging desert tortoises in California (1990–1995). J. Wildlife Dis. 39, 35–56 (2003).
Christopher, M. M. et al. Reference intervals and physiologic alterations in hematologic and biochemical values of free-ranging desert tortoises in the Mojave Desert. J. Wildlife Dis. 35, 212–238 (1999).
Catchen, J., Hohenlohe, P. A., Bassham, S., Amores, A. & Cresko, W. A. Stacks: an analysis tool set for population genomics. Mol. Ecol. 22, 3124–3140 (2013).
Langmead, B. & Salzberg, S. L. Fast gapped-read alignment with Bowtie 2. Nat. Methods 9, 357–359 (2012).
Li, H. et al. The Sequence Alignment/Map format and SAMtools. Bioinformatics 25, 2078–2079 (2009).
Alexander, D. H., Novembre, J. & Lange, K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 19, 1655–1664 (2009).
R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/ (2017).
Jombart, T., Devillard, S. & Balloux, F. Discriminant analysis of principal components: a new method for the analysis of genetically structured populations. BMC Genetics 11, 94 (2010).
Jombart, T. adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics 24, 1403–1405 (2008).
Nychka, D., Furrer, R., Paige, J. & Sain, S. fields: Tools for spatial data. Retrieved from, https://doi.org/10.5065/D6W957CT (2015).
Hijmans, R. J. raster: Geographic Data Analysis and Modeling. Comprehensive R Archive Network (CRAN). Retrieved from, https://CRAN.R-project.org/package=raster (2016).
Caye, K., Deist, T. M., Martins, H., Michel, O. & François, O. TESS3: fast inference of spatial population structure and genome scans for selection. Mol. Ecol. Res. 16, 540–548 (2015).
Berry, K. H. & Christopher, M. M. Guidelines for the field evaluation of desert tortoise health and disease. J. Wildlife Dis. 37, 427–450 (2001).
Phillips, S. J., Anderson, R. P. & Schapire, R. E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 190, 231–259 (2006).
Phillips, S. J. & Dudík, M. Modeling of species distributions with Maxent: new extensions and a comprehensive evaluation. Ecography 31, 161–175 (2008).
Dyer, R. J. gstudio: Tools Related to the Spatial Analysis of Genetic Marker Data. Retrieved from, https://github.com/dyerlab/gstudio (2016).
Excoffier, L., Smouse, P. E. & Quattro, J. M. Analysis of molecular variance inferred from metric distances among DNA haplotypes: application to human mitochondrial DNA restriction data. Genetics 131, 479–491 (1992).
Smouse, P. E. & Peakall, R. Spatial autocorrelation analysis of individual multiallele and multilocus genetic structure. Heredity 82, 561–573 (1999).
Graves, T., Chandler, R. B., Royle, J. A., Beier, P. & Kendall, K. C. Estimating landscape resistance to dispersal. Landsc. Ecol. 29, 1201–1211 (2014).
van Etten, J. R Package gdistance: Distances and routes on geographical grids. J. Stat. Softw. 76, 1–21 (2017).
McRae, B. H., Dickson, B. G., Keitt, T. H. & Shah, V. B. Using circuit theory to model connectivity in ecology, evolution, and conservation. Ecology 89, 2712–2724 (2008).
Peterman, W. E. ResistanceGA: An R package for the optimization of resistance surfaces using genetic algorithms. Methods Ecol. Evol. https://doi.org/10.1111/2041-210X.12984 (2018).
Row, J. R., Knick, S. T., Oyler-McCance, S. J., Lougheed, S. C. & Fedy, B. C. Developing approaches for linear mixed modeling in landscape genetics through landscape-directed dispersal simulations. Ecol. Evol. 7, 3751–3761 (2017).
Zuur, A. F., Ieno, E. N., Walker, N. J., Saveliev, A. A. & Smith, G. Mixed Effects Models and Extensions in Ecology with R (Springer, 2009).
Bates, D., Maechler, M., Bolker, B. & Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48 (2015).
Goslee, S. C. & Urban, D. L. The ecodist package for dissimilarity-based analysis of ecological data. J. Stat. Softw. 22, 1–19 (2007).
Ruiz-Gonzalez, A., Cushman, S. A., Madeira, M. J., Randi, E. & Gómez-Moliner, B. J. Isolation by distance, resistance and/or clusters? Lessons learned from a forest-dwelling carnivore inhabiting a heterogeneous landscape. Mol. Ecol. 24, 5110–5129 (2015).
Foll, M. & Gaggiotti, O. A genome-scan method to identify selected loci appropriate for both dominant and codominant markers: a Bayesian perspective. Genetics 180, 977–993 (2008).
Quinlan, A. R. & Hall, I. M. BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26, 841–842 (2010).
Paradis, E. pegas: an R package for population genetics with an integrated-modular approach. Bioinformatics 26, 419–420 (2010).
Crandall, K., Bininda-Emonds, O., Mace, G. & Wayne, R. Considering evolutionary processes in conservation biology. Trends Ecol. Evol. 15, 290–295 (2000).
Schwartz, M. K., Luikart, G. & Waples, R. S. Genetic monitoring as a promising tool for conservation and management. Trends Ecol. Evol. 22, 25–33 (2007).
Bohonak, A. J. Dispersal, gene flow, and population structure. Quart. Rev. Biol. 74, 21–45 (1999).
Rico, Y. et al. Re-evaluating the spatial genetic structure of Agassiz’s desert tortoise using landscape genetic simulations. Desert Tortoise Council, Las Vegas, Nevada (2015).
Guisan, A. & Thuiller, W. Predicting species distribution: offering more than simple habitat models. Ecol. Lett. 8, 993–1009 (2005).
Rowlands, P., Johnson, H., Ritter, E. & Endo, A. The Mojave Desert in Reference Handbook on the Deserts of North America (ed. Bender, G. L.) 103–162 (Greenwood Press, 1982).
Rowlands, P. G. Regional bioclimatology of the California Desert in The California Desert: An Introduction to Natural Resources and Man’s Impact (eds. Rowlands, P. G. & Latting, J.) 95–134 (Latting Books, 1995).
Rowlands, P. G. Vegetational attributes of the California Desert Conservation Area in The California Desert: An Introduction to Natural Resources and Man’s Impact (eds. Rowlands, P. G. & Latting, J.) 135–212 (Latting Books, 1995).
Edwards, T. et al. Testing Taxon Tenacity of Tortoises: evidence for a geographical selection gradient at a secondary contact zone. Ecol. Evol. 5, 2095–2114 (2015).
Wallace, C. S. & Gass, L. Elevation Derivatives for Mojave Desert Tortoise Habitat Models (U.S. Geological Survey, 2008).
Nagy, K. A. & Medica, P. A. Physiological ecology of desert tortoises in southern Nevada. Herpetologica 42, 73–92 (1986).
Andersen, M. C. et al. Regression‐tree modeling of desert tortoise habitat in the central Mojave Desert. Ecol. Appl. 10, 890–900 (2000).
Mack, J. S., Berry, K. H., Miller, D. M. & Carlson, A. S. Factors affecting the thermal environment of Agassiz’s desert tortoise (Gopherus agassizii) cover sites in the central Mojave Desert during periods of temperature extremes. J. Herpetol. 49, 405–414 (2015).
Turner, F. B. & Randall, D. C. Net production by shrubs and winter annuals in southern Nevada. J. Arid Environ. 17, 23–36 (1989).
Jennings, W. B. & Berry, K. H. Desert tortoises (Gopherus agassizii) are selective herbivores that track the flowering phenology of their preferred food plants. PLoS One, 10, e0116716–32 (2015).
Lovich, J. E. et al. Not putting all their eggs in one basket: bet-hedging despite extraordinary annual reproductive output of desert tortoises. Biol. J. Linn. Soc. 115, 399–410 (2015).
Medica, P. A., Bury, R. B. & Luckenbach, R. A. Drinking and construction of water catchments by the desert tortoise, Gopherus agassizii, in the Mojave Desert. Herpetologica 36, 301–304 (1980).
Peterson, C. C. Ecological energetics of the desert tortoise (Gopherus agassizii): effects of rainfall and drought. Ecology 77, 1831–1844 (1996).
Duda, J. J., Krzysik, A. J. & Freilich, J. E. Effects of drought on desert tortoise movement and activity. J. Wildl. Manag. 63(1), 181–1,192 (1999).
Henen, B. T. Seasonal and annual energy budgets of female desert tortoises (Gopherus agassizii). Ecology 78, 283–296 (1997).
Barrows, C. W., Henen, B. T. & Karl, A. E. Identifying climate refugia: A framework to inform conservation strategies for Agassiz’s desert tortoise in a warmer future. Chelonian Conserv. Biol. 15, 2–11 (2016).
Burge, B. L. Movements and behavior of the desert tortoise, Gopherus agassizii (University of Nevada, 1977).
Marlow, R. W. & Tollestrup, K. Mining and exploitation of natural mineral deposits by the desert tortoise, Gopherus agassizii. Animal Behav. 30, 475–478 (1982).
Averill-Murray, R. C. & Hagerty, B. E. Translocation relative to spatial genetic structure of the Mojave Desert tortoise. Gopherus agassizii. Chelonian Conserv. Biol. 13, 35–41 (2014).
Edwards, T. & Berry, K. H. Are captive tortoises a reservoir for conservation? An assessment of genealogical affiliation of captive Gopherus agassizii to local, wild populations. Conserv. Genet. 14, 649–659 (2013).
Heaton, J. S. et al. Spatially explicit decision support for selecting translocation areas for desert tortoises. Biodivers. Conserv. 17, 575–590 (2008).
Ferguson, G. W. & Talent, L. G. Life-history traits of the lizard Sceloporus undulatus from two populations raised in a common laboratory environment. Oecologia 93, 88–94 (1993).
Hews, D. K., Thompson, C. W., Moore, I. T. & Moore, M. C. Population frequencies of alternative male phenotypes in tree lizards: geographic variation and common-garden rearing studies. Behav. Ecol. Sociobiol. 41, 371–380 (1997).
U.S. Fish and Wildlife Service. Range-wide monitoring of the Mojave Desert Tortoise (Gopherus agassizii): 2013 and 2014 Annual Reports (U.S. Fish and Wildlife Service, 2015).
Beaumont, M. A. & Nichols, R. A. Evaluating loci for use in the genetic analysis of population structure. Proc. R. Soc. B. 263, 1619–1626 (1996).
Çilingir, F. G. et al. Conservation genomics of the endangered Burmese roofed turtle. Conserv. Biol. 31, 1469–1476 (2017).
Barton, N. H. Linkage and the limits to natural selection. Genetics 140, 821–841 (1995).
Cutter, A. D. & Payseur, B. A. Genomic signatures of selection at linked sites: unifying the disparity among species. Nat. Rev. Genet. 14, 262–274 (2013).
Zhu, T. et al. Effects of thymosin β4 on wound healing of rat palatal mucosa. Int. J. Mol. Med. 34, 816–821 (2014).
Shin, S.-H. et al. Thymosin Beta4 regulates cardiac valve formation via endothelial-mesenchymal transformation in zebrafish embryos. Mol. Cells 37, 330–336 (2014).
Seals, D. F. & Courtneidge, S. A. The ADAMs family of metalloproteases: multidomain proteins with multiple functions. Genes Dev. 17, 7–30 (2003).
Dickinson, R. E. & Duncan, W. C. The SLIT-ROBO pathway: a regulator of cell function with implications for the reproductive system. Reproduction 139, 697–704 (2010).
Qiu, X. et al. Crystal structure of cholesteryl ester transfer protein reveals a long tunnel and four bound lipid molecules. Nat. Struct. Mol. Biol. 14, 106–113 (2007).
Henen, B.T. Desert tortoise diet and dietary deficiencies limiting tortoise egg production at Goffs, California. Desert Tortoise Council, Las Vegas, Nevada Symposium (1993).
Barzilai, N. et al. Unique lipoprotein phenotype and genotype associated with exceptional longevity. JAMA 290, 2030–2040 (2003).
Hengl, T. et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS One 12, e0169748–40 (2017).
Fick, S. E. & Hijmans, R. J. WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315 (2017).
Wallis, I. R., Henen, B. T. & Nagy, K. A. Egg size and annual egg production by female desert tortoises (Gopherus agassizii): The importance of food abundance, body size, and date of egg shelling. J. Herpetol. 33. 394 (1999).
Acknowledgements
We thank Dr. Fredric Janzen and one anonymous reviewer for insightful comments and suggestions about the manuscript. MCAGCC samples were collected under United States Fish & Wildlife Service Permits TE 17730-5 and BO 8-8-11-F-65R and analyzed per MCAGCC Department of Navy Contracts N62470-13-D-8016 FZ02, N62473-11-D-2224 [0054 & 0060], N62473-08-C-3504 and N62473-09-D-2603 [to 6399 and 7276]. J. Still and J. Galina-Mehlman performed ddRAD-seq library preparation and sequencing. Use of trade, product, or firm names in this publication is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Author information
Authors and Affiliations
Contributions
S.S.R., Y.R. and R.W.M. conceived the experiments. K.H.B., A.E.K. and B.T.H. provided the samples. Y.R. and T.E. performed laboratory procedures. S.S.R. processed and analyzed the data, and wrote the first draft of the manuscript, A.E.K., B.T.H. and R.W.M. provided financial support. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sánchez-Ramírez, S., Rico, Y., Berry, K.H. et al. Landscape limits gene flow and drives population structure in Agassiz’s desert tortoise (Gopherus agassizii). Sci Rep 8, 11231 (2018). https://doi.org/10.1038/s41598-018-29395-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-29395-6
This article is cited by
-
Genetic and ecological consequences of recent habitat fragmentation in a narrow endemic plant species within an urban context
Biodiversity and Conservation (2021)
-
Using movement to inform conservation corridor design for Mojave desert tortoise
Movement Ecology (2020)
-
Genes in space: what Mojave desert tortoise genetics can tell us about landscape connectivity
Conservation Genetics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.