Introduction

Controlling complex networks1,2,3 is of great importance in many applications, such as social, biological and technical networks. For example, it has been shown that understanding network controllability can help identify genes responding to viral infection4 and genes related to cancer5, as well as assist analyzing metabolic process6.

A network is said to be controllable if it can be driven from any initial state to a desirable state in finite steps by exerting external control signals on some selected nodes1, which are called driver nodes7, input nodes8 or control nodes9. The controllability of a network can be determined by Kalman’s controllability rank condition1 if the weight of each edge is known, or Lin’s structural controllability theory10 if only a zero or non-zero value of each edge’s weight is known. As edge weights of many real networks cannot be precisely measured and are often unknown, the structural controllability theory has been widely adopted recently to analyze biological systems, such as protein interaction network4, 5, 11, signaling pathway network12, and gene regulatory network13, 14.

Based on the structural controllability theory, one approach7,8,9, 15, 16 assumes that a node can control only one of its outgoing neighbor. Therefore, input nodes of a network can be inferred by finding a maximum matching of the network, which is consisted of the set of maximum edges that do not share nodes3. The unmatched nodes related to a maximum matching constitute a Minimum Input nodes Set, or MIS. However, this approach can be only applied to directed networks. Another approach5, 17, 18 assumes that a node can control all of its outgoing edges independently, that is, a node can output different signals for each edge. Under this assumption, a minimum node dominate set (MDS) can be used to control the network18. This approach may be more reasonable for artificial networks and can be applied to undirected networks.

Based on above frameworks, extensive works have been done about control principles of complex networks. It has been shown that the size of an MIS is closely related to the node degree distribution of the network7. Interestingly, the fraction of input nodes is primarily determined by the nodes of low in- and out-degrees16. The concepts of input nodes and MIS are also extensively used in analyzing many biological networks, e.g., identifying important proteins in biological networks4, 5, analyzing interbank networks19, and increasing the effectiveness of selective modulation of brain networks20.

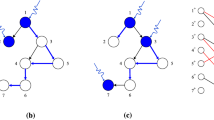
Unfortunately, maximum matching is not unique for most networks21 (Fig. 1), so there may exist numerous MISs. Although these MISs have the same size, they may have different input nodes. We call a node in an MIS a possible input node. Apparently, all possible input nodes are the union of all MISs. It is important to find all possible input nodes for understanding the controllability of a complex network. For example, finding all possible input nodes may help understand the roles of nodes in control systems22, design suitable MISs under different constraints8, and identify critical genes on signaling pathways14. Finding all possible input nodes is essentially an enumeration problem. While enumeration problems have been extensively studied, such as for enumerating all maximum matchings23, 24 or all maximally-matchable edges25, there are very few works on how to find all unmatched nodes. To solve this problem, a previous approach22 first computes a maximum matching and then assess if an unmatched node is a possible input node by removing it to test if its removal may result in a larger maximum matching. The computational complexity of finding a maximum matching is O(N 1/2 L) and the evaluation process is O(NL) on a network of N nodes and L edges, for a total complexity of O(NL) for this method.

Figure 1
figure 1

An example network with two MISs. (A) An example network; (B) two MIS of the network D 1 = {1, 3}, D 2 = {1, 2}; (C) all possible input nodes of the network, which form the union of both MISs.

Full size image

We developed an efficient algorithm for finding all possible input nodes of a network. We proved that all possible input nodes could be identified by a simple modification to a maximum matching algorithm. The complexity of our algorithm is O(N 1/2 L), which is the same as the complexity of the maximum matching algorithm. Because our algorithm does not need to evaluate every node of the network, it runs several orders of magnitude faster than the previous method22 on large networks. Furthermore, our algorithm can also output the substituting nodes set for each input nodes. Because some input nodes may not be suitable to be inputted control signals due to some economic or technical constraints, these substituting nodes can be used to replace the original input nodes and obtain new MISs with some input nodes replaced.

Method

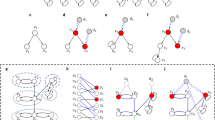
Consider a directed network G(V, E) over a set of nodes V and a set of edges E. To find an MIS of a directed network G(V, E), we first convert G(V, E) to an equivalent undirected bipartite graph B(V in , V out , E) (Fig. 2A,B). The bipartite graph is built by splitting the node set V into two node sets V in and V out, where a node n in G is converted to two nodes n in and n out in B, and nodes n in and n out are, respectively, connected to the in-edges and out-edges of node n.

Figure 2
figure 2

An example of a maximum matching of a network. (A) A directed network; (B) its corresponding bipartite graph; (C) A maximum matching of the bipartite graph. An unmatched node in the in-set is an input node; (D) Two alternating paths corresponding to the maximum matching in (C).

Full size image

Now consider maximum matching. A matching is a set of edges that share no common node. A node is called a matched node if it is connected to a matching edge, or unmatched node, otherwise. A matching with the maximum number of edges is called a maximum matching. In an undirected bipartite graph, an alternating path is a path whose edges are alternate in and out matching. An augmenting path is an alternating path whose two end nodes are unmatched nodes. Based on the Berge theorem26, a matching M * is a maximum matching if there is no augmenting path in B(v 1 , v 2 , E) with respect to M *. The input nodes are the unmatched nodes in V in corresponding to a maximum matching of bipartite graph B(V in, V out, E). The unmatched nodes in V in corresponding to any maximum matching form an MIS of G. If there exists a perfect matching in the network, the MIS can be any node of the network based on the Minimum Input Theorem7.

Because maximum matching is not unique for most networks, there may exist many MISs. The union of all MISs contains all possible input nodes. We now show that to find all possible input nodes of a network, we only need to compute one maximum matching without enumerating all MISs or evaluating all matched nodes as done before in ref. 22.

Theorem 1: Given a directed network G and a maximum matching M of G, a node n is a possible input node if it satisfies one of the following two conditions:

  1. 1.

    Node n is an input node related to M;

  2. 2.

    The in-node n in of the bipartite graph B can be reached from an input node m in related to M through an alternating path p nm .

Proof: It is sufficient to prove condition 2.

Sufficiency. Suppose that node n satisfies condition 2. Apparently, the length of p nm must be even because both node n in and m in are in the set V in of bipartite graph B. Therefore, the alternating path p nm must start with an unmatched edge connected to m in and end with a matched edge connected to node n in. Change the types of all edges of p nm , i.e., change the matched edges to unmatched and the unmatched edges to matched, then the new path p’ nm is still an alternating path. Consequently, we get a new maximum matching M’. Clearly, the node n in is not matched by M’ and m in is matched by M’. Therefore, node n is an input node of MIS D’ = D-{m} + {n}.

Necessity. Let node n in be matched in M and be unreachable by any input node related to M. Suppose that node n in is not matched by a maximum matching M’. Node n in must have at least one in-edge because it is matched by M. Therefore, there must be an alternating path p nm related to M’ which starts with unmatched node n in and end with a matched node m in. Now consider the path p nm under the maximum matching M. The length of p nm must be even because nodes n in and m in are both in the set V in. Therefore, the alternating path p nm must end with an unmatched node m in related to M because n in is matched by M. This contradicts the fact that n in cannot be reached by any input node related to M, which completes the proof.

The above proof implies an important fact that any of the nodes reachable from an input node can be used to replace the original input node and obtain a new MIS. Therefore, we have the following corollary:

Corollary 1: Consider an MIS D and one of its input node m ∈ D, let K m be the set of the nodes that satisfied condition 2 of Theorem 1. For every node n ∈ K m , D’ = D − {m} + {n} is an MIS.

Based on Theorem 1, the proof to the corollary is trivial. Corollary 1 suggests how to find the substituting nodes for an input node. For example, in Fig. 3, the substituting nodes of input node 4 are node 8 and node 6. If node 4 is not suitable for accepting control signals, we can use either node 8 or node 6 to substitute node 4, and the new MIS would be {8, 10} or {6, 10}.

Figure 3
figure 3

An example of the process of algorithm All_Input(G). (A) A sample network and its maximum matching (red edges) (B) the corresponding bipartite graph; (C) In the last step of the algorithm, we search for alternating paths from unmatched nodes. The nodes on the alternating paths in V in are nodes {8, 6, 9}, and the input nodes are {4, 10}. Therefore, all possible input nodes of the network are {4, 6, 8, 9, 10}. The substituted nodes of input node 4 are node 8 and node 6, and those of input node 10 is node 9. Therefore, if node 4 or 10 is not suitable to be inputted control signals, we can use the corresponding substituted nodes to input control signals and regain full control of the network.

Full size image

The significance of Theorem 1 and Corollary 1 is that all possible input nodes can be identified by some alternating paths of the input nodes of any given MIS. This observation leads to a novel two-step approach to identification of all possible input nodes, i.e., we first compute an MIS and then consider all of its alternating paths. Moreover, these two steps can be combined using a simple modification to the Hopcroft–Karp maximum matching algorithm for undirected graphs27. The basic idea of the Hopcroft–Karp algorithm is to iteratively find all augmenting paths corresponding to the matching M at hand, and then to derive a larger matching M’. A maximum matching is obtained when no augmenting path can be founded. The last step of the algorithm is exactly to look for all alternating paths starting from the input nodes of the maximum matching. Therefore, all possible input nodes can be obtained in the last step of Hopcroft–Karp algorithm based on Theorem 1.

The above idea and steps can be formulated in Algorithm All_Input(G) for finding all possible input nodes in network G, which is listed as follows:

All_Input(G):

  1. 1.

    For a directed network G(V, E), let B(V out, V in, E) be its corresponding bipartite graph; let the initial matching M = null;

  2. 2.

    Find all the alternating paths of all unmatched nodes in V in, denoted as AP = {P 1, P 2 … P n }, and let the nodes of AP in V in as candidate results;

  3. 3.

    If AP contain augmenting paths, expand all augmenting paths and obtain a new matching M’; clear all candidate nodes, M = M’; return to step 2;

  4. 4.

    If AP contain no augmenting path, the candidate nodes are all possible input nodes, and the set of the unmatched nodes is an MIS of G.

Figure 3 illustrates an example of All_Input(G) on a small network. The time complexity of the above algorithm is the same as that of the Hopcroft-Karp algorithm, which is O(N 1/2 L).

Result

To assess the efficiency of the new algorithm, which was coded in JAVA, we compared it with the previous algorithm22. The source code of our algorithm and the previous algorithm is available in the supplementary information. The comparison was done on a Windows 7 workstation with a quad-core Intel i7-3770 processor of 3.9 GHz and 32GB DDR3 1600MHz memory.

We considered 13 synthetic networks, in which the number of nodes n varied from 105 to 5 × 106 and the average degree <k> varied from 6 to 16. Networks were generated with Gephi28 based on the Scale-Free Network model29. The experimental results on these networks showed that our algorithm outputted the same results set yet significantly outperformed previous algorithm22 (Fig. 4). With a small network with n = 105, our algorithm achieved 52x speedup compared to the previous algorithm22. With a larger network with n = 5 × 106, our algorithm achieved 7330x speedup with the execution time being only 3.276 seconds. Note that the speedup increases with the average degree.<k> (Fig. 4A), which indicates that our algorithm has better performance on dense networks. The details of the results are listed in Table 1.

Figure 4
figure 4

Speedup of our algorithm as compared to the previous algorithm22. (A) Speedup as a function of the average degree when n = 106; (B) Speedup as a function of the number of nodes when average degree < k > = 8. The networks are generated based on Scale-Free Network model29 with r in = r out = 3.

Full size image
Table 1 Comparison of the execution time of some synthetic networks.
Full size table

Next, we evaluated the performance of the algorithm on some real networks. These networks were selected based on their diversity of topological structures. These networks include biological networks, social networks, and Internet networks. The size of these networks varied from very small (E. Coli network, 423 nodes) to very large (Amazon network, 4 × 106 nodes). The results shown in Table 2 indicated that our algorithm also significantly outperformed the previous algorithm. On large networks, such as Amazon or Twitter, the results can be obtained within 10 seconds, resulting in an almost 104x speedup compared to the previous algorithm.

Table 2 Comparison of the execution time of some real networks.
Full size table

As we have proven in corollary 1, our algorithm can also output the substituting nodes for each input node. Figure 5A shows an example of St. Marks foodweb43, which has 13 input nodes in an MIS. We computed the substituting nodes for each input node and showed the alternating paths between them in Fig. 5B. Interestingly, the size of the substituting nodes set of each input node is different, indicating some input nodes are more robust in controlling the network. The experimental results on other real networks are similar (Fig. 6). Note that some input nodes have the same number of substituting nodes because they are linked to the same set of substituting nodes, e.g., those of TRN-Yeast-131 and Ythan foodweb44 in Fig. 6.

Figure 5
figure 5

Input nodes and their substituted set of St. Marks foodweb43. (A) Network topology of St. Marks foodweb. The input nodes are green nodes. (B) All 13 Input nodes and their substituted nodes. We showed the alternating paths which connected the input nodes and their substituted nodes. The red edges are the matching edges.

Full size image
Figure 6
figure 6

Percentage of substituted nodes for each input node of real networks. The networks we used are Kohonen37, TRN-Yeast-131, Ythan foodweb44 and TRN-Yeast-231. The vertical axis represents the percentage of substituted nodes p i  = s i /N, where s i is the number of substituted nodes of input node i, and N is the total number of the nodes. The horizontal axis shows an MIS, in which the input nodes are sorted based on s i by descending order.

Full size image

Conclusion

We developed an efficient algorithm for finding all possible input nodes for controlling complex networks. We proved that all possible input nodes can be efficiently identified along with computing an MIS without increasing the overall complexity beyond finding the MIS. Therefore, our algorithm offers a significant speedup over the previous algorithm on both synthetic networks and many large real networks. Furthermore, our algorithm can also output the substituted nodes set for each input node. It means that once we computed an MIS, we can immediate obtain all the substituting nodes for the MIS. Thanks to its efficiency, the new algorithm makes it possible to study controllability of large real-world networks and will have many potential applications in diverse areas.

Data availability

All data generated or analyzed during this study are included in this article (and its Supplementary Information files).