Introduction

The study of single magnetic rare-earth (RE) atoms adsorbed on metallic1,2,3 and insulating4 solid surfaces recently became a subject of intense research. These “single-atom” magnets serve as benchmarks in a quest for the ultimate size limit of magnetic information storage. The major advance of observing the magnetic remanence was recently reported for the Ho adatom on MgO substrate4. The stable magnetic quantum state of the adatom was found on the time scale of 1500 s at 10 K temperature.

There is an ongoing debate whether the magnetic moment on Ho atom on Pt(111) surface (Ho@Pt) can be stable on the long time scale. Recent inelastic electron tunneling spectroscopy (IETS) measurements1 reported the moment lifetime up to 700 s below 1 K temperature, due to the single-ion magnetic anisotropy. However, the x-ray spectroscopy experiments2 have shown that the ground state of Ho is magnetically unstable, with no magnetic remanence. Moreover, the newer IETS experimental data3 did not see neither signatures of the spin-flip excitations nor spin-based telegraph noise for Ho atoms. This indicates that the 4f electrons do not contribute to the spin polarized tunneling processes in RE atoms on metals.

Theoretical calculations can shed light on the controversy concerning the magnetic state of Ho@Pt. The two |J = 8, J z  = ±8〉 magnetic ground states pointing into and out of the Pt(111) surface were inferred from ab initio density functional theory (DFT) calculations1. The multiplet calculations2 with the parameters chosen to reproduce the x-ray magnetic circular dichroism (XMCD) spectra resulted in |J = 8, J z  = ±6〉 ground states. Further analysis5 critically reexamined the XMCD data analysis2, and confirmed qualitatively the magnetically unstable ground state of Ho.

Up to date, conventional DFT and DFT+Coulomb U 6, 7 (DFT+U) methodologies were used in the calculations of Ho@Pt1, 3. Their main role was to identify the most favorable adsorption site and the optimal height for the Ho adatom above the Pt surface layer. While DFT+U can describe the chemical inertness of the 4f shell, it does not include the atomic multiplet effects, and can yield ambiguous results for the magnetic moments, or valence stability8. Recently, the combination of DFT with the dynamical mean field theory9 in a form of the Hubbard-I approximation (HIA)10 has been applied to the elemental RE, and is shown to be superior to the DFT+U and semiempirical ligand field (or equvalently crystal field) theory11. It opens new opportunities to treat the electronic structure of complex materials containing RE elements.

Here, we report the charge self-consistent electronic structure theory of Ho@Pt performed by combining DFT with the exact diagonalization (ED)12 of a single-impurity Anderson model13. In this approach, the DFT electronic structure obtained by the relativistic version14, 15 (with the spin-orbit coupling (SOC) included) of the full-potential linearized augmented plane wave method (FP-LAPW)16 is consistently extended to account for the full structure of the 4f-orbital atomic multiplets and their interaction with the conduction bands17. Previously, the method was used to treat the 4f-electron materials in paramagnetic phase8, 18, and we extend it to the spin-polarized case.

Methodology

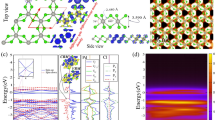
We use the 3 × 3 × 1 supercell model with twenty seven Pt atoms (three layers), and the rare-earth adatom which is placed either in the hcp(-Ho@Pt) or the fcc(-Ho@Pt) hollow positions atop the Pt(111) surface (see supplemental Fig. S1). The symmetry of both adsorption sites is C 3v . The difference between hcp-Ho@Pt and fcc-Ho@Pt originates from the different placement of the Pt atoms in the sub-surface layer. The optimal heights for the rare-earth Ho adatoms above the Pt surface layer are taken from ref. 1 as h hcp  = 4.386 bohr and h fcc  = 4.348 bohr.

In the RE atoms the 4f electrons are mainly responsible for the magnetic moment, and the external spd electrons make only a discreet contribution to it. Their role, however, can not be disregarded, since these outer electrons strongly infuence the electronic and magnetic properties of the system. Therefore, we consider the multi-orbital Hamiltonian10 H = H 0 + H int. H 0 is the one-particle Hamiltonian found from ab initio electronic structure calculations of a supercell; H int is the on-site Coulomb interaction10 describing the f-electron correlation. We assume that electron interactions in the s, p, and d shells are well approximated in DFT.

The DFT+ED calculations are performed in the charge self-consistent implementation described in section “Theoretical methods and computational details”. The effects of the interaction Hamiltonian H int on the electronic structure are accounted by a one-particle selfenergy Σ, which is constructed with the aid of an auxiliary impurity model Eq. (1) describing the complete seven-orbital 4f shell. The band Lanczos method12 is employed to find the lowest-lying eigenstates of the many-body Hamiltonian H imp and to calculate the one-particle Green’s function G imp and the selfenergy Σ in the subspace of the localized f orbitals {ϕ γ } at low temperature (k B T = 1/500 eV). The Coulomb U values of 7.03 eV, and the exchange J of 0.83 eV were used, which are in the ballpark of commonly accepted values of U and J for the rare earths19, 20.

Results

The XMCD measurements2 are performed in an external magnetic field (up to 7 T) assuming the magnetic saturation of the Ho@Pt system. Therefore, we have performed the spin-polarized calculations assuming the magnetic saturation of the Ho-adatom f-shell. In these calculations, we applied HIA and ED to DFT with the non-spin-polarized exchange-correlation functional21 in order to exclude the contribution of f-intraorbital exchange field into the double-counting W dc 22. The exchange splitting Δex in Eq. (1), which corresponds to the interorbital exchange energy between the 4f and 5d states of Ho, was varied as a parameter in a range from 5 meV to 15 meV (see the section “Theoretical methods and computational details” for further explanation of the Δex choice). We have examined that it is enough to produce a fully spin-polarized solution and the selfenergy in Eq. (1).

First, we discuss the spin-polarized DFT+ED for the fcc-Ho@Pt. The f-states occupation 〈n f 〉 changes only a little - from 10.17 to 10.16 - with the change of Δex. The calculated ground state magnetic properties are shown in Table 1 in comparison with the XMCD2 experiments. The values of spin moment \({M}_{S}=-2\langle {S}_{z}\rangle {\mu }_{B}/\hslash \) change only a little with the change of Δex. The changes in orbital moment \({M}_{L}=-\langle {L}_{z}\rangle {\mu }_{B}/\hslash \), and the magnetic dipole moment \({M}_{D}=-6\langle {T}_{z}\rangle {\mu }_{B}/\hslash \) are somewhat bigger indicating enhancement of the orbital polarization with an increase of Δex. Due to simultaneous increase of the orbital M L and the the magnetic dipole M D moments, the ratio \({R}_{LS}=\tfrac{{M}_{L}}{{M}_{S}+{M}_{D}}=1.20\) does not change with an increase of Δex. It is somewhat smaller than the XMCD result2 R LS 1.51 ± 0.09, but still in reasonable agreement with the experiment. The magnitude of the total moment \(\langle {J}_{z}\rangle ={M}_{S}\mathrm{/2}+{M}_{L}\) of 6.6 (Δex = 5 meV), and 6.8 (10–15 meV) exceeds somewhat the experimental 〈J z 〉 of 5.34–5.502. It is closer to 〈J z 〉 = 62 obtained in the multiplet calculations than to 〈J z 〉 = 81 inferred from DFT+U. Note that in the presence of the crystal-field interaction, the values of the magnetic moment M J  = M S  + M L obtained from the data of Table 1 are smaller than the maximum magnetic moment g J J = 9.84, where g J  = 1.23 is the Lande factor and J = 8.00 is the expectation value of the total moment calculated for the ground state of Eq. (1). No noticeable differences are found for Ho@Pt in fcc and hcp positions (see supplemental Table S2).

Table 1 Spin (M S ), orbital (M L ), M S plus magnetic dipole M D moments (in μ B ), and the total 〈J z 〉 = M S /2 + M L for the fcc-Ho adatom on Pt(111) with different values of the exchange splitting Δex, in comparison with DFT+U1, 3 and experimental data2.
Full size table

The total and j = 5/2, 7/2 projected f orbital density of states (fDOS) for the spin-polarized fcc-Ho@Pt and Δex = 10 meV is shown in Fig. 1(A). DFT+ED yields for the occupied 4f-states the first multiplet peak at ~4 eV below E F , and for the empty states at ~2.5 eV, consistent with the bulk hcp-Ho PES23. Effect of spin-polarization is illlustrated in Fig. 1(B) where the spin-resolved fDOS is shown. The spin-↑ intensities lie at ~7–8 eV below E F , and the spin-↓ at ~4–6 eV below E F . The empty states of spectrum at ~2–4 eV are practically fully spin-polarized. There is no surprise that these states are dominated by the j = 7/2 contribution since the j = 5/2 states are fully occupied for the f 10 manifold.

Figure 1
figure 1

The total and j = 5/2, 7/2 projected fDOS for the fcc-Ho@Pt(111) (A); the spin projected fDOS for the fcc-Ho@Pt(111) (B).

Full size image

The energy splitting of the seventeen lowest many-body eigenvalues of Eq. (1), which correspond to the expectation value of J f  = 8.00, are shown in Fig. 2(A) (also see supplemental Table S3). The lowest energy is \(|J=8,{J}_{z}=7.00\rangle \) state, next to it is the state \(|J=8,{J}_{z}=5.98\rangle \) which is 10 meV higher in the energy, and the third state is \(|J=8,{J}_{z}=0.02\rangle \), higher in the energy by 6 meV. This energy difference determines the magnetic anisotropy energy (MAE) barrier of 16 meV to turn the magnetization from the out-of-plane to the in-plane orientation. This value is about three times smaller than the MAE obtained by DFT+U1.

Figure 2
figure 2

Scheme of quantum many-body levels of the lowest J f  = 8.00 multiplet obtained in Eq. (1) with the Δ CF parameters for spin-polarized calculations and Δ ex  = 10 meV (A); with the Δ CF parameters for non-spin-polarized calculations (B).

Full size image

The experimental IETS results1 yield the spin excitations at the 5 meV and 8 meV energies. However, in the further experiments3, no signature of inelastic signal distinguishable from the substrate spectrum was found. We have calculated the model IETS spectra for the polarized fcc-Ho@Pt as given in the Supplemental material. We found shallow steps at the low energies ±10 meV, and other steps at the energies over 40 meV. Thus, our results disagree with earlier experiments of Miyamachi et al.1. Whether the calculated steps can be seen in the experiments depends on the intensity of the differential conductance (see the Eq. (S3) in Supplemental Material). Since it is proportional to the very small hybridization strength ~17 meV, the IETS intensity will be further reduced. We conclude that our results do not contradict qualitatively the experimental findings3.

Once the magnetic field is switched off, the adatom becomes non-magnetic. The self-consistent solution of Eq. (3) for paramagnetic state (Δex = 0) represents the final state after the demagnetization. In this state, the f-electron count 〈n f 〉 changes to 10.5, and the crystal field changes as well (see supplemental Table S4 for comparison between spin-polarized and paramagnetic ΔCF). It is not surprising, since the symmetry of the many-body ground state of Eq. (1) is changing, inducing the changes in the local occupation matrix \({n}_{{\gamma }_{1}{\gamma }_{2}}\) and corresponding effective LDA+U potential V U in Eq. (3). This effect is neglected in semiempirical ligand field theory.

The energy splitting of the seventeen lowest many-body eigenvalues of Eq. (1) in paramagnetic state are shown in Fig. 2(C)) (also see supplementary Table S3). The lowest energy is the \(|J=8,{J}_{z}=\pm 7.95\rangle \) state, in agreement with 〈J z 〉 = ±81. Next to it is the state \(|J=8,{J}_{z}=\pm 5.36\rangle \) which is 6.5 meV higher in the energy, and the second exited state is \(|J=8,{J}_{z}=0.0\rangle \), higher in the energy by 1.4 meV. This energy difference determines the so-called zero-field splitting energy barrier of 7.9 meV, which is twice as large as given by the ligand field theory2. Note, that application of the external magnetic field of 7 T to this paramagnetic state in Eq. (1) will not produce the spin-polarized solution shown in Fig. 2(A), since the parameters of the Eq. (1) hamiltonian are different (ΔCF, Δex, e f ). This difference is determined by the charge self-consistency, and the 5d–4f interorbital exchange coupling. This spin-polarized ground state can not be described by simple re-population of the Zeeman-split non-magnetic many-body levels.

The transition from the initial magnetically polarized state to the final paramagnetic state in the quantum regime is a complex problem24 and we leave the theoretical description of the magnetization dynamics for future considerations. Nonetheless, we notice that if we assume Δex = 0 while keeping all other parameters in Eq. (1) the same as in the spin-polarized case, the ground state changes to \(|J=8,{J}_{z}=0\rangle \) and the adatom becomes magnetically unstable (see Supplemental Material).

Conclusions

To summarize, comparison between spin-polarized and paramagnetic DFT+ED solutions for Ho@Pt shows that the correct 4f magnetic state in the presence of the external magnetic field can not be correctly described by simple re-population of the Zeeman-split many-body levels of a non-magnetic semiempirical hamiltonian. It is due to non-negligible role of the interaction between 4f and 5d electrons. We emphasize the role of 5d–4f interorbital exchange polarization in modification of the 4f shell energy spectrum, and overrule the existence of the magnetic 〈J z 〉 = 8 ground state1.

Theoretical Method and Computational Details

The multi-orbital impurity solver includes the full spherically symmetric Coulomb interaction, the spin-orbit coupling (SOC), the crystal field term (CF) describing the Coulomb interaction of the f-shell with other electrons, and the inter-orbital exchange field acting on the f-shell from other electrons. The corresponding Hamiltonian can be written as ref. 13

$$\begin{array}{rcl}{H}_{{\rm{imp}}} & = & \sum _{\begin{array}{c}kmm^{\prime} \\ \sigma \sigma ^{\prime} \end{array}}{[{\epsilon }^{k}]}_{mm^{\prime} }^{\sigma \,\sigma ^{\prime} }{b}_{km\sigma }^{\dagger }{b}_{km^{\prime} \sigma ^{\prime} }+\sum _{m\sigma }{\epsilon }_{f}{f}_{m\sigma }^{\dagger }{f}_{m\sigma }\\ & & +\sum _{mm^{\prime} \sigma \sigma ^{\prime} }{[\xi {\bf{l}}\cdot {\bf{s}}+{{\rm{\Delta }}}_{{\rm{CF}}}+{{\rm{\Delta }}}_{{\rm{ex}}}{s}_{z}]}_{mm^{\prime} }^{\sigma \,\sigma ^{\prime} }{f}_{m\sigma }^{\dagger }{f}_{m^{\prime} \sigma ^{\prime} }\\ & & +\sum _{\begin{array}{c}kmm^{\prime} \\ \sigma \sigma ^{\prime} \end{array}}({[{V}^{k}]}_{mm^{\prime} }^{\sigma \,\sigma ^{\prime} }{f}_{m\sigma }^{\dagger }{b}_{km^{\prime} \sigma ^{\prime} }+{\rm{h}}.{\rm{c}}.)\\ & & +\frac{1}{2}\sum _{\begin{array}{c}mm^{\prime} m^{\prime\prime} \\ m^{\prime\prime\prime} \sigma \sigma ^{\prime} \end{array}}{U}_{mm^{\prime} m^{\prime\prime} m^{\prime\prime\prime} }{f}_{m\sigma }^{\dagger }{f}_{m^{\prime} \sigma ^{\prime} }^{\dagger }{f}_{m^{\prime\prime\prime} \sigma ^{\prime} }{f}_{m^{\prime\prime} \sigma ^{\prime} },\end{array}$$
(1)

where \({f}_{m\sigma }^{\dagger }\) creates an electron in the 4f shell and \({b}_{m\sigma }^{\dagger }\) creates an electron in the “bath” that consists of those host-band states that hybridize with the impurity 4f shell. The energy position \({\epsilon }_{f}\) of the impurity level, and the bath energies \({\epsilon }^{k}\) are measured from the chemical potential μ. The parameters ξ, Δex, and matrix ΔCF specify the strength of the SOC, the exchange field, and the size of CF, acting on the f-shell. The parameter matrices V k describe the hybridization between the 4f states and the bath orbitals at energy \({\epsilon }^{k}\). The bath parameters V k and \({\epsilon }^{k}\) are determined from the LDA Green function G LDA(z) as described in ref. 18, and are shown in supplemental Table S1. The Ho f-shell SOC parameter ξ = 0.28 eV in Eq. (1) was determined from LDA calculations.

The exchange splitting Δex in Eq. (1) corresponds to the interorbital exchange energy between the 4f and mainly 5d states of Ho, J fd m 5d 22, where J fd is ~0.1 eV25, and m 5d is the magnetic moment of the 5d states. As follows from the DFT and DFT+U calculations3 as well as from our own calculations, the m 5d does not exceed 0.1 μ B . It sets Δex = 10 meV as an energy scale for the J fd m 5d . Note that Δex exceeds the maximum external magnetic field value (0.4 meV) used in the XMCD experiments by an order of magnitude, and we did not include this field in the calculations.

The many-body Hamiltonian H imp is solved employing the band Lanczos method12 and the selfenergy is obtained. The local Green’s function G(z) in the subspace of the localized spinorbitals {ϕ γ , γ = (lmσ)}, defining the f manifold of the rare-earth adatom, is calculated17 as

$$G(z)={[{G}_{0}^{-1}(z)+{\rm{\Delta }}{\epsilon }_{\sigma }-{\rm{\Sigma }}(z)]}^{-1},$$
(2)

where G 0(z) is the non-interacting Green’s function, and \({\rm{\Delta }}{\epsilon }_{\sigma }\) are chosen to ensure the \({n}_{f}^{\sigma }\) occupations equal to the given number of spin-↑, ↓ correlated electrons. The matrix \({n}_{{\gamma }_{1}{\gamma }_{2}}=-\frac{1}{\pi }\,{\rm{Im}}{\int }_{-\infty }^{{E}_{{\rm{F}}}}\,{\rm{d}}z\,{[G(z)]}_{{\gamma }_{1}{\gamma }_{2}}\) is used to construct an effective LDA+U potential V U , which is inserted into Kohn–Sham-like equations:

$$[-{\nabla }^{2}+{V}_{{\rm{LDA}}}({\bf{r}})+{V}_{U}+\xi ({\bf{l}}\cdot {\bf{s}})]\,{{\rm{\Phi }}}_{{\bf{k}}}^{b}({\bf{r}})={\epsilon }_{{\bf{k}}}^{b}{{\rm{\Phi }}}_{{\bf{k}}}^{b}({\bf{r}}).$$
(3)

Note that the DFT contributions to the effective potential V LDA in Eq. (3) are corrected to exclude the double-counting of the f-states non-spherical contributions to the DFT and DFT+U parts of the potential17.

These equations are iteratively solved until self-consistency over the charge density is reached. In each iteration, a new Green’s function G 0(z), and a new value of the 4f-shell occupation are obtained from the solution of Eq. (3). Subsequently, a new selfenergy Σ(z) corresponding to the updated 4f-shell occupation is constructed. Finally, the next iteration is started by evaluating the new local Green’s function, Eq. (2). The self-consistent procedure defined by Eqs 1–3 was repeated until the convergence of the 4f-manifold occupations \({n}_{f}^{\uparrow ,\downarrow }\) was better than 0.01.

The CF matrix ΔCF in Eq. (1) is obtained by projecting the solutions of Eq. (3) into the {ϕ γ } local f-shell basis,

$${[H]}_{{\gamma }_{1}{\gamma }_{2}}={\int }_{-\infty }^{+\infty }\,{\rm{d}}\epsilon \epsilon {[N(\epsilon )]}_{{\gamma }_{1}{\gamma }_{2}},$$
(4)

where, \({[N(\epsilon )]}_{{\gamma }_{1}{\gamma }_{2}}\) is an f-projected density of states (fDOS) matrix. The matrix elements of ΔCF are then obtained by removing the interacting LDA+U potential \({[{V}_{U}]}_{{\gamma }_{1}{\gamma }_{2}}\) and SOC \({[\xi {\bf{l}}\cdot {\bf{s}}]}_{{\gamma }_{1}{\gamma }_{2}}\) from the local hamiltonian Eq. (4).

Since some electron-electron interaction energy is already included in LDA, the potential V U in Eq. (3) includes the so-called double-counting correction W dc. Due to a self-consistency condition \({\epsilon }_{f}=-{W}_{dc}\) 17, it determines the mean position of the interacting f-level in Eq. (1), and controls the number of f-electrons. For the bulk Ho, the positions and the spectral shape of the occupied 4f-states are in a reasonable agreement with experimental valence-band photoelectron spectroscopy (PES)23, when the “around-mean-field” (AMF)6 flavour for W dc is used (see Supplemental Material). Therefore, we used this W dc in the Ho@Pt calculations.