Abstract
The current model of the Episodic Temporal Generalization task, where subjects have to judge whether pairs of auditory stimuli are equal in duration, predicts that results are scale-free and unaffected by the presentation order of the stimuli. To test these predictions, we conducted three experiments assessing sub- and supra-second standards and taking presentation order into account. Proportions were spaced linearly in Experiments 1 and 2 and logarithmically in Experiment 3. Critically, we found effects of duration range and presentation order with both spacing schemes. Our results constitute the first report of presentation order effects in the Episodic Temporal Generalization task and demonstrate that future studies should always consider duration range, number of trials and presentation order as crucial factors modulating performance.
Similar content being viewed by others
Introduction
Time has been a matter of ardent debate across many disciplines1. Within neuroscience, not only does it constitute an important topic in its own right2, but it also impinges on the field’s fundamental areas of inquiry, including consciousness3, motor control4, memory5, artificial intelligence6, and neural dynamics7. Likewise, the study of timing abnormalities is pivotal for research on pathologies such as Parkinson’s disease and schizophrenia8. In brief, understanding timing, time perception, and their neural basis proves fundamental for contemporary neuroscience9.
Even though many relevant models and theories have been proposed10, some basic questions are still unsolved. Here we aimed to address one of them: is timing equal across different scales?
Multiple studies have addressed this issue based on a distinction between sub- and supra-second durations11, with contradictory results. Some studies show that response variability increases linearly as a function of duration, thus following Weber’s Law, in a range that goes from a few hundred milliseconds to a few seconds –see ref. 12 for a systematic investigation. However, other reports indicate that this linear property stops holding at some point between 1 and 2 seconds –see ref. 13 for a review.
This controversy is epitomized by the antinomy between two major conceptual frameworks used to account for timing mechanisms in the brain: the “common timing hypothesis” and the “distinct timing hypothesis”14. Whereas the former assumes a single timing mechanism irrespective of duration, the latter posits dissociable mechanisms for sub- and supra-second durations.
A typical approach to study time perception is to have participants judge whether two durations are equal15. This so-called Temporal Generalization task has two main versions for humans. In the original one16, participants learn a standard duration at the beginning of the experiment and are then presented with several to-be-compared durations. Instead, in the Episodic version17, subjects judge the durations of two successive stimuli on a trial-by-trial basis. Stimuli are constructed in a similar way for both versions: a set of comparison durations is generated multiplying a standard duration (e.g., 400 ms, or values from a range such as 300 to 500 ms) by a series of ratios (e.g., 0.5, 1, 1.5). In the original version, a clear standard is learnt at the beginning and participants judge whether it is equal to each of the following durations. In the Episodic version, presentation order is counterbalanced so that in half of the trials the standard comes first and in the other half it comes second.
Both tasks showed a similar pattern of results with sub-second durations: the obtained psychometric functions were asymmetrical, with a higher proportion of “equal” responses on the right tail, that is, when the ratio was higher than 116, 17. The same pattern was found using the original standard version, with durations ranging from 2 up to 8 seconds18. Importantly, results were superimposed between duration ranges when plotted in a relative scale, that is, as a function of the proportion between standard and comparison durations. This was interpreted as confirmation of the common timing hypothesis. However, no studies have yet used supra-second durations as standards in the Episodic version.
Traditionally, temporal generalization results have been interpreted within Scalar Expectancy Theory, which, in brief, states that durations are estimated via accumulation of pulses. Within this framework, in the temporal generalization task subjects would compare the two values of the estimated durations and then decide based on their normalized absolute difference19. Therefore, according to this model, results should not be affected by presentation order of the stimuli, something known as the “balance condition”20, nor by duration range. Presentation order effects have been shown in a wide variety of time perception tasks, termed “time-order-errors” (TOE) within this context (see ref. 21 for a review), but never in the Episodic Temporal Generalization (ETG) task. In fact, no previous studies using the task tested for any effect of this kind17, 22,23,24.
In addition, evaluating symmetry with linearly spaced proportions (i.e. 0.25, 0.50, 0.75, 1, 1.25, 1.50, 1.75), as is usually the case with the ETG task17, 19, 22, implies an unbalanced comparison. Symmetry within this setting would indicate that a similar amount of “equal” responses were obtained when comparing, for example, ratios 0.25–1 (1:4) and 1.75–1 (1.75:1) or vice versa (4:1 and 1:1.75). A more meaningful comparison would arise from using logarithmically spaced proportions, so that, following the example above, ratios, 0.25–1 (1:4) and 4–1 (4:1) could be contrasted.
Moreover, the property of superposition has been tested via visual inspection or ANOVAs17, 19, none of which is robust to such an end. The first one proves inadequate because it does not establish a decisional boundary to accept or reject hypotheses, and the second because it can produce spurious results when used with proportional data25, 26. A more convenient approach would be to compare Weber Fractions (WF) between duration ranges and test whether they remain constant, in which case a scalar relationship could be assumed to exist between them.
Against this background, our study pursued three main objectives. First, we tested the prediction, derived from the traditional ETG model, that presentation order had no effect on performance. Second, we examined the symmetry/asymmetry of the temporal generalization gradients taking presentation order into account and using linear and logarithmically spaced proportions, so that symmetry could be properly assessed. Third, we compared WFs of sub- and supra-second ranges to test their compliance with the scalar property of timing.
To address these aims, we conducted three experiments. Experiment 1 was designed with a number of trials similar to that of previous studies using the task17, 22 and comprised linearly spaced proportions. As taking presentation order into account reduced the number of trials of each ratio to a half, we conducted Experiment 2, in which the same task was administered but with a threefold increase in trials. Experiment 3 had the same number of trials as Experiment 2 but proportions were logarithmically spaced. With this combination of experiments, we aimed to address some critical gaps in the ETG framework.
Method
Participants
Eighteen subjects participated in Experiment 1 (F = 10; \(\overline{{\rm{x}}}\) age = 24.22; s age = 3.12; \(\overline{{\rm{x}}}\) years of education = 17.78; s years of education = 3.83), 20 in Experiment 2 (F = 10; \(\overline{{\rm{x}}}\) age = 25.47; s age = 3.94; \(\overline{{\rm{x}}}\) years of education = 18.87; s years of education = 3.04), and 18 in Experiment 3 (F = 11; \(\overline{{\rm{x}}}\) age = 24.39; s age = 3.53; \(\overline{{\rm{x}}}\) years of education = 18.94; s years of education = 2.82), after signing informed consent. Subjects participated in only one of the experiments. All of them reported normal hearing, right-handedness, and absence of neurological and psychiatric antecedents, and they were naïve as to the purpose of the study. The experiments were approved by the local ethics committee (INECO Foundation) and were conducted in accordance with the Declaration of Helsinki.
Stimuli
Auditory stimuli were 500-Hz tones created and delivered using Matlab (Mathworks Inc.) and Psychtoolbox27 through Sennheiser HD202 headphones at 65db on a MacBook Pro notebook. Before the experiment, the software created 7 blocks of 16 trials; half of the stimuli corresponded to the Sub-Second condition and the other half to the Supra-Second one. For each trial, a Standard (S) duration was selected from a uniform distribution, ranging from 300 to 500 ms in the Sub-Second condition, and from 1200 to 2000 ms in the Supra-Second one. Then, S was multiplied by one of 7 ratios (linearly spaced in Experiments 1 and 2: 0.25, 0.50, 0.75, 1.0, 1.25, 1,50, 1.75; logarithmically spaced in Experiment 3: 0.25, 0.40, 0.63, 1, 1.59, 2.52, 4) to create a Comparison (C) duration, so that on each block there was one trial of each ratio for each condition (i.e., 7 ratios × 2 conditions = 14 trials). An additional 1.0 ratio trial was then added to each condition. Finally, the order of the trials was randomized and each trial was assigned a random counterbalanced presentation order so that on half of the trials the S was presented first, and on the other half the first stimulus presented was C. In Experiment 1 a total of 112 trials were obtained from each subject in an average of 16 minutes (σ = 36 s). In Experiment 2, the task was repeated three times with 5 minute breaks between them, therefore 336 trials were obtained from each subject, in 62 minutes on average (σ = 9 m). In Experiment 3, 336 trials were obtained from each subject in 68 minutes on average (σ = 5 m). See Supplementary Figures 1, 2, and 3 (S1, S2, and S3) for further details.
Procedure
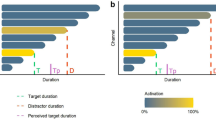
Participants were informed that they would hear sequences of two tones and that their task was to decide whether both sounds had the same duration (Fig. 1). Each trial started with a 5-s inter-trial interval that was followed by the presentation of a tone, a gap (randomly chosen from a uniform distribution from 400 to 600 ms), and a second tone. Participants had to respond with their right hand on the notebook keyboard. To indicate that the tones were equal, they had to press the down arrow key with their index finger; to indicate that they were not, they had to press the right arrow with their middle finger. Importantly, post-task debriefing showed that although all participants detected two duration ranges, none of them realized that there were standard and comparison distributions.
Data Analysis
Statistical analyses were performed on R software28. All subjects were included in them. Following previous reports18, we plotted the temporal generalization gradients as a function of comparison durations and tested their asymmetry by comparing the proportion of “equal” responses on the three Ratios below 1 (C-Shorter), against the proportion of “equal” responses on the three Ratios above it (C-Longer) using Wilcoxon Signed-Rank tests. Statistical results were corrected for multiple comparisons using the Holm-Bonferroni method.
In order to characterize the TOE, we first estimated the point of subjective equality (PSE) using the smoothing spline curve-fitting method from Matlab’s (Mathworks Inc.) Curve Fitting Toolbox (with automatic selection of the smoothing parameter), and finding the maximum of the resulting curve. We then defined the TOE following Fechner’s definition of constant error (CE)21:
where PSE denotes the point of subjective equality and st the standard duration. Within this context, the sign of CE denotes the sign of the TOE when the standard is presented first. When the standard was presented in second place, the sign of the TOE was computed as st – PSE. We report the magnitude of the TOE as a percentage of the standard (%TOE)29. %TOEs were submitted to a rm-ANOVA with standard duration (Sub-second/Supra-second) and order (S-C/C-S) as factors.
Weber Fractions (WF) were calculated as:
where DL denotes the difference limen and PSE the point of subjective equality30. Within this analysis, the PSE and DL were calculated as the mean and standard deviation of a fitted Gaussian function, respectively. WFs were submitted to a rm-ANOVA with standard duration (Sub-second/Supra-second) and order (S-C/C-S) as factors. To control that the PSEs did not differ between methods we compared them using a Wilcoxon Signed-Rank test.
Effect sizes in all cases were calculated via generalized eta squared (η2 G)31; these were considered as small if η2 G = 0.02, medium if η2 G = 0.13, and large if η2 G = 0.26. Holm-Bonferroni corrected post hoc t-tests were used for pairwise comparisons.
Results
Experiment 1
The proportion of “equal” responses (PE) for each ratio and duration, when collapsing presentation orders, is shown in Fig. 2. Even though visual inspection suggests that both temporal generalization gradients were asymmetrical, Wilcoxon tests proved that this was significant only in the Sub-Second condition (V = 135.5, p < 0.01), where a higher PE was found when C-Ratio > 1. In the Supra-Second condition, the difference was not significant (V = 220, p = 0.12).
The PE for each ratio and duration when including presentation order as an additional variable is shown in Fig. 3. Visual inspection again suggests that all temporal generalization gradients were asymmetrical, which, in this case, was true for all comparisons. In the Sub-Second condition, both presentations orders, S-C (V = 30, p < 0.05) and C-S (V = 40, p < 0.05) had a greater PE when C-Ratio > 1. In the Supra-Second condition, the C-S presentation order also had a greater PE when C-Ratio > 1 (V = 139, p < 0.01). Interestingly, in the S-C order of the Supra-Second condition the asymmetry was in the opposite direction, that is, the PE was higher when C-Ratio < 1 (V = 1, p < 0.01). Visual inspection also suggests that the temporal generalization gradients of the Supra-second condition are shifted to the left and right in the S-C and C-S orders, respectively.
This part of the analysis revealed that the asymmetries of temporal generalization gradients were not equal between the two duration ranges considered. Moreover, when presentation order of the stimuli was taken into account, results suggested that this occurred because of a shift of the temporal generalization gradients in the Supra-Second condition that depended on the presentation order of the stimuli (Fig. 3). The presentation order effect in combination with the asymmetrical gradients (the latter probably due to the linear spacing of the comparison proportions) undermined the comparison of WFs, as they rely on the estimation of the spread of the temporal generalization gradients. This analysis was therefore not carried out for this Experiment.
In Experiment 1, we used a similar amount of trials than previous studies that employed the task17, 22. Partitioning trials by presentation order left approximately 3–4 trials per ratio and order combination for each subject, which might have led to inaccurate results. In order to overcome this limitation we replicated Experiment 1 but this time we collected three times more trials per subject.
Experiment 2
The PE for each ratio and duration, when collapsing presentation orders, is shown in Fig. 4. Visual inspection again suggests that both temporal generalization gradients were asymmetrical, and again Wilcoxon tests proved that this was significant only in the Sub-Second condition (V = 89, p < 0.001), where a higher PE was found when C-Ratio > 1. In the Supra-Second condition, the difference was not significant (V = 282, p = 0.17).
The PE for each ratio and duration when including presentation order as an additional variable is shown in Fig. 5. Visual inspection once more suggests that all temporal generalization gradients were asymmetrical, which, in this case, was true for all comparisons but one. In the Sub-Second condition, the S-C presentation order had a higher PE when C-Ratio > 1 (V = 1, p < 0.001) and in the C-S order the difference was not significant (V = 76, p = 0.29). As in Experiment 1, in the Supra-Second condition, the C-S presentation order had a greater PE when C-Ratio > 1 (V = 12, p < 0.001) and in the S-C order the asymmetry was in the opposite direction, that is, the PE was higher when C-Ratio < 1 (V = 196, p < 0.01). Visual inspection also suggests that temporal generalization gradients are shifted but this time also in the Sub-second range. Interestingly, the directions of the shifts seem to be inverted between duration ranges and orders.
This part of the analysis revealed that, as in Experiment 1, the asymmetries of the temporal generalization gradients were not equal between the duration ranges considered in the study. Experiment 2 showed that when collecting more trials per subject, the asymmetry of the C-S order of the Sub-second condition was not significant, in contrast with Experiment 1. Furthermore, Experiment 2 suggests that the shifts of the temporal generalization gradients that were observed in the Supra-second condition also appeared in the Sub-second range but with opposite sign.
In order to characterize the presentation order effect (TOE) we computed the %TOE of each subject of Experiment 2 (Fig. 6) and conducted a rm-ANOVA. It showed a main effect of Duration (F 1,19 = 93.15, p < 0.001, η2 G = 0.48), with a higher %TOE in the Sub-second condition; a main effect of Order (F 1,19 = 27.36, p < 0.001, η2 G = 0.14), with a higher %TOE in the S-C order; and a non-significant Duration x Order interaction (F 1,19 = 0.58, p = 0.45, η2 G = 0.009). The %TOE was positive in the Sub-second range (\(\overline{{\rm{x}}}\) = 5.68) and negative in the Supra-second range (\(\overline{{\rm{x}}}\) = −13.79).
Time-order-errors. Violin plots of the magnitude and sign of the time-order-errors for each duration range and presentation order, as percentage of standard duration, across participants of Experiment 2 (linearly spaced ratios). The corresponding ANOVA showed a main effect of duration range (p < 0.001, η2 G = 0.48), a main effect of presentation order (p < 0.001, η2 G = 0.14) and a non-significant interaction (p = 0.45, η2 G = 0.009).
Again, the combination of the different presentation order effects and the asymmetrical gradients hindered the comparison of WFs, so no such analysis was conducted. The linear spacing of the comparison proportions probably caused the asymmetrical gradients. We therefore conducted a third experiment, this time with logarithmically spaced ratios, so that the resulting gradients presumably became more symmetrical and allowed a meaningful comparison of WFs.
Experiment 3
The PE when collapsing presentation order is shown in Fig. 7. Here, visual inspection suggests that temporal generalization gradients were not asymmetrical, which Wilcoxon tests proved to be correct (Sub-second: V = 417.5, p = 0.28; Supra-second: V = 274, p = 1).
The PE for each ratio and duration when including presentation order as an additional variable is shown in Fig. 8. Visual inspection suggests that all temporal generalization gradients were symmetrical, which was true for all comparisons but one. The only significantly asymmetrical gradient was found in the Supra-second S-C condition with a higher PE when C-Ratio < 1 (V = 108, p < 0.05). All remaining comparisons were not significant (Sub-second S-C: V = 66, p = 1; Sub-second C-S: V = 144.5, p = 0.54; Supra-second C-S: V = 32, p = 0.08).
The TOE analysis from Experiment 3 (Fig. 9) showed a main effect of Order (F 1,17 = 2344.41, p < 0.001, η2 G = 0.90), with a higher %TOE in the C-S order; a main effect of Duration (F 1,17 = 16.00, p < 0.001, η2 G = 0.21), with a higher %TOE in the Sub-second condition; and a non-significant Duration x Order interaction (F 1,17 = 4.20, p = 0.056, η2 G = 0.01). The %TOE was negative in the C-S order (\(\overline{{\rm{x}}}\) = −29.38) and positive in the S-C order (\(\overline{{\rm{x}}}\) = 24.42).
Time-order-errors. Violin plots of the magnitude and sign of the time-order-errors for each duration range and presentation order, as percentage of standard duration, across participants of Experiment 3 (logarithmically spaced ratios). The corresponding ANOVA showed a main effect of duration range (p < 0.001, η2 G = 0.21), a main effect of presentation order (p < 0.001, η2 G = 0.90) and a non-significant interaction (p = 0.056, η2 G = 0.01).
The more symmetrical gradients obtained using logarithmically spaced ratios allowed us to compute and compare WFs. We first tested that the PSEs obtained for this analysis did not differ from the PSEs obtained in the TOE analysis. Wilcoxon tests proved that they were not significantly different (V = 1024, p = 0.1). We then proceeded to the WF analysis (Fig. 10), where the rm-ANOVA showed a main effect of Duration (F 1,17 = 15.87, p < 0.001, η2 G = 0.12), with higher values in the Sub-second condition; a main effect of Order (F 1,17 = 5.34, p < 0.05, η2 G = 0.02), with higher values in the C-S order; and a significant Duration x Order interaction (F 1,17 = 7.25, p < 0.05, η2 G = 0.04). Holm-Bonferroni corrected post hoc tests revealed that the WFs of the S-C order of the Supra-second condition differed from all others (vs. Sub-second S-C: p < 0.001; vs. Sub-second C-S: p < 0.01; vs. Supra-second C-S: p < 0.01). All remaining comparisons were not statistically significant (Sub-second S-C vs. Sub-second C-S: p = 0.63; Sub-second S-C vs. Supra-second C-S: p = 0.24; Sub-second C-S vs. Supra-second C-S: p = 0.52).
Weber Fractions. Violin plots of the Weber Fractions for each duration range and presentation order, across participants of Experiment 3 (logarithmically spaced ratios). The corresponding ANOVA showed a main effect of duration range (p < 0.001, η2 G = 0.12), a main effect of presentation order (p < 0.05, η2 G = 0.02) and a significant interaction (p < 0.05, η2 G = 0.04). Holm-Bonferroni corrected post hoc tests showed that the S-C order of the Supra-second condition differed from all others (vs. Sub-second S-C: p < 0.001; vs. Sub-second C-S: p < 0.01; vs. Supra-second C-S: p < 0.01) and that all remaining comparisons were not statistically significant.
Discussion
The first aim of our study was to assess whether performance on the ETG task is sensitive to presentation order effects. We showed that TOEs appeared in the two duration ranges under consideration, and that this effect held for both linear and logarithmic spacing. Interestingly, effect sizes between Experiments 2 and 3 were inverted. In the linearly spaced experiment, the duration range showed a large effect (η2 G = 0.48) and presentation order a medium one (η2 G = 0.14), while the use of logarithmically spaced proportions showed a large effect for presentation order (η2 G = 0.90) and a medium one for duration range (η2 G = 0.21). Together with the observed signs of the TOEs, these results reveal different patterns between experiments. In the linearly spaced experiment, subjects overestimated the first sound in the Sub-second condition and the second sound in the Supra-second range. Instead, when proportions were logarithmically spaced, they overestimated the Comparison duration, with a smaller influence of its position and duration range.
TOEs have been reported in a wide range of tasks21 but never in the ETG task. They have mainly been reported when the standard duration was fixed across trials, even though they have been also reported in experiments where both stimuli varied32, 33. Having a standard that repeats from trial to trial implies that memory and learning can play a major role in the obtained results and might also introduce other sources of variance. For example, subjects might realize the existence of the standard and try to find it on each trial. Besides, incorrectly identifying the comparison duration as the standard could also lead to distortions in the memory representation of the standard. In our case, standard (and comparison) durations varied from trial to trial, so these factors can be assumed to have had a lower impact.
Our results constitute the first report of TOEs in the ETG task. Presentation order was not taken into account in previous studies17, 22,23,24 and, as our results clearly show, it must be considered when employing the task.
The second aim of our study was to test the symmetry/asymmetry of the temporal generalization gradients while taking presentation order into account, and assessing linear and logarithmically spaced proportions. Experiment 1 showed right asymmetrical gradients in the S-C and C-S orders of the Sub-second condition and also in the C-S order of the Supra-second range. In the S-C order of the latter the asymmetry emerged in the opposite direction. Experiment 2 showed inverted asymmetries between ranges, that is, right asymmetrical gradients were found in the S-C order of the Sub-second condition and in the C-S order of the Supra-second range. Conversely, left asymmetrical gradients were found in the C-S order of the Sub-second condition and in the S-C order of the Supra-second range. Experiment 3 showed that using logarithmically spaced durations yielded more symmetrical gradients but still, results from the S-C order of the Supra-second condition were significantly left asymmetrical.
Wearden and colleagues19 modelled the Episodic version results by modifying the Church and Gibbon model. The original model was created to account for the results of the same task in rats34, where the resulting gradient was not asymmetrical. Wearden added the mean of the two durations as normalizing factor, to account for the asymmetry in humans. Thus, the formula for a “yes-equal” response became:
where t 1 * and t 2 * are the two durations to be compared, m is their mean (the normalizing factor), and b* is a threshold. The higher the values of m, the higher the chances of being below the threshold and giving a “yes-equal” response. This way, it predicts only right asymmetrical gradients, despite the presentation order and duration range of the stimuli. Our results showed left asymmetrical gradients that reflected presentation order effects, therefore contradicting these predictions. Consequently, our findings represent a new empirical constraint calling for a modification of the model.
Our results also have implications for other models of time perception. Apart from Wearden’s proposal, there are other two mainstream models aimed to account for two-interval forced-choice temporal experiments, namely, the Internal Reference Model35,36,37 and the Sensation Weighting Model21, 32, 38. Both have been developed for comparative judgements (where subjects have to establish which of the two stimuli was longer), but they have been recently extended to equality judgements36. The former was developed for experiments in which the standard was fixed across trials and therefore does not apply in our case. The basic formulation of the Sensation Weighting Model is:
where w 1 and w 2 are the weighting coefficients of the internal representations of the first (X 1 ) and second (X 2 ) stimuli, and u is a constant to adjust the mean of D. According to this formulation, subjects would judge that durations were equal if a < D < b, where a and b are thresholds. This account implies that the first and second sounds are weighted differently by the subject and therefore predicts and accounts for the time-order-errors that we observed in our study (see ref. 39). Within this framework, the TOEs arise from the formation of a reference level in the midrange of the stimuli, which is then weighted in the comparisons38. This would explain why the TOE was not observed in the Sub-second range when using a small number of trials (Experiment 1) and appeared when such number was increased (Experiment 2), as the reference level requires time to be established. In this regard, our results raise the question of whether the Supra-second range is more susceptible to this influence.
Previous reports of the Temporal Generalization task18 claimed that the fact that temporal generalization gradients superimposed across sub- and supra-second ranges supported Scalar Expectancy Theory, one of the emblematic frameworks assuming the “common timing hypothesis”40. We showed that they are different for these two ranges when using the Episodic version of the task and taking presentation order into account, due to time-order-errors. However, presentation order effects have been observed in a wide range of tasks, including non-temporal tasks (i.e. weight comparison)38, 41. They are considered to be caused by processes beyond the specificity of the temporal domain21 and therefore our results should not be interpreted as being in line with the “distinct timing hypothesis”, but rather as the refutation of predictions made by a model that supports the “common timing hypothesis”.
Moreover, the property of superposition has been previously tested via visual inspection or ANOVAs17, 19, neither of which is sufficiently robust to such an end. The former is not suitable for hypothesis testing and the latter because of its problems when used on proportional data25, 26, as is the case with temporal generalization gradients.
Consequently, the third objective of our study was to compare the WFs of the two ranges. If they were not significantly different, they could be assumed to comply with Weber’s Law. One possible confound in this comparison is that chronometric counting has been shown to improve performance for durations above ~1.18 s42 and to reduce the coefficients of variation (as the WF), therefore disrupting the scalar property of variance43. Interestingly, our results showed that WFs were smaller only for the S-C presentation order of the Supra-second range while not being significantly different in all the remaining comparisons. In other words, WFs were different between duration ranges for one presentation order but not for the other, and they were also different between presentation orders in the Supra-second range. If the decrease in the WFs observed in the S-C order of the Supra-second range was caused by chronometric counting, it could be expected to have influenced the C-S order in a similar way, which was not the case. Whichever the cause may be, the answer to the question of whether sub- and supra-second timing rely on the same or different mechanisms remains elusive and future studies will be required to elucidate it.
In sum, even though our results do not provide clear evidence in favour or against the scalar property of human timing in the sub- and supra-second duration ranges, they do demonstrate the importance of taking stimulus duration range and presentation order into account. This new constraint should be factored in future studies employing the task and in the models derived from it.
Limitations
Our study has two main limitations. The first one is that the supra-second condition included, as comparison durations, stimuli that were below the 1s range. Thus, it was not a purely supra-second condition but rather a condition in which the standard duration was supra-second. Future studies could use a pure supra-second condition by choosing a longer standard duration range. The second limitation is that we did not explicitly prevent chronometric counting. We did so to make our conditions comparable. Including a concurrent numerical task within durations of around half a second would have been methodologically incorrect. Not only would that pose higher cognitive demands than if included in a supra-second duration, but it would also be perceptually difficult. It’s worth noting that when chronometric counting was explicitly encouraged in the original version of the task18, the resulting psychometric functions were symmetrical when collapsing presentation orders, which was not the case in our study. To overcome this limitation, modifications of the experimental design will be required.
Conclusions
Our study constitutes the first report of time-order-errors in the ETG task. We also showed differences that arise from the use of sub- and supra-second standards and from linear and logarithmically spaced proportions. In addition, we demonstrated that the current model of the task fails to account for the observed results. Presentation order was not taken into consideration by previous studies and, as our results clearly show, should always be considered. Moreover, we found that the number of trials used influences the observed pattern of results and should therefore also be considered as a crucial factor. Finally, we showed that Weber Fractions also vary as a function of duration range and presentation order. These results afford relevant empirical constraints for future research on the topic.
References
Buccheri, R., Saniga, M., Stuckey, W. M. & North Atlantic Treaty Organization. Scientific Affairs Division. The nature of time–geometry, physics, and perception. (Kluwer Academic Publishers, 2003).
Eagleman, D. M. Time and the Brain: How Subjective Time Relates to Neural Time. Journal of Neuroscience 25, 10369–10371, doi:10.1523/JNEUROSCI.3487-05.2005 (2005).
Dennett, D. C. & Kinsbourne, M. Time and the observer: The where and when of consciousness in the brain. Behavioral and Brain Sciences 15, 183–201 (1992).
Berret, B. & Jean, F. Why Don’t We Move Slower? The Value of Time in the Neural Control of Action. J Neurosci 36, 1056–1070, doi:10.1523/JNEUROSCI.1921-15.2016 (2016).
Buzsaki, G. Cognitive neuroscience: Time, space and memory. Nature 497, 568–569, doi:10.1038/497568a (2013).
Chittaro, L. & Montanari, A. Temporal representation and reasoning in artificial intelligence: Issues and approaches. Annals of Mathematics and Artificial Intelligence 28, 47–106, doi:10.1023/a:1018900105153 (2000).
Johnson, H. A., Goel, A. & Buonomano, D. V. Neural dynamics of in vitro cortical networks reflects experienced temporal patterns. Nat Neurosci 13, 917–919, doi:10.1038/nn.2579 (2010).
Allman, M. J. & Meck, W. H. Pathophysiological distortions in time perception and timed performance. Brain 135, 656–677, doi:10.1093/brain/awr210 (2012).
Finnerty, G. T., Shadlen, M. N., Jazayeri, M., Nobre, A. C. & Buonomano, D. V. Time in Cortical Circuits. Journal of Neuroscience 35, 13912–13916, doi:10.1523/JNEUROSCI.2654-15.2015 (2015).
Ivry, R. B. & Schlerf, J. E. Dedicated and intrinsic models of time perception. Trends in Cognitive Sciences 12, 273–280, doi:10.1016/j.tics.2008.04.002 (2008).
Chen, L., Bao, Y. & Wittmann, M. Editorial: Sub- and Supra-Second Timing: Brain, Learning and Development. Front Psychol 7, 747, doi:10.3389/fpsyg.2016.00747 (2016).
Merchant, H., Zarco, W. & Prado, L. Do we have a common mechanism for measuring time in the hundreds of millisecond range? Evidence from multiple-interval timing tasks. Journal of Neurophysiology 99, 939–949, doi:10.1152/jn.01225.2007 (2008).
Grondin, S. In Neurobiology of Interval Timing Vol. 829 (eds Hugo Merchant & Victor de Lafuente) 17–32 (Springer New York, 2014).
Rammsayer, T. H. & Troche, S. J. In search of the internal structure of the processes underlying interval timing in the sub-second and the second range: a confirmatory factor analysis approach. Acta Psychol (Amst) 147, 68–74, doi:10.1016/j.actpsy.2013.05.004 (2014).
Grondin, S. Timing and time perception: a review of recent behavioral and neuroscience findings and theoretical directions. Atten Percept Psychophys 72, 561–582, doi:10.3758/APP.72.3.561 (2010).
Wearden, J. H. Temporal generalization in humans. Journal of Experimental Psychology: Animal Behavior Processes 12, 134–144, doi:10.1037/0097-7403.18.2.134 (1992).
Wearden, J. H. & Bray, S. Scalar timing without reference memory? Episodic temporal generalization and bisection in humans. Q J Exp Psychol B 54, 289–309, doi:10.1080/713932763 (2001).
Wearden, J. H., Denovan, L. & Haworth, R. Scalar timing in temporal generalization in humans with longer stimulus durations. Journal of Experimental Psychology: Animal Behavior Processes 23, 502 (1997).
Wearden, J. H. Decision processes in models of timing. Acta Neurobiol Exp (Wars) 64, 303–317 (2004).
Falmagne, J.-C. Elements of psychophysical theory. (Clarendon Press; Oxford University Press, 1985).
Hellström, A. The time-order error and its relatives: Mirrors of cognitive processes in comparing. Psychological Bulletin 97, 35–61 (1985).
Wearden, J. H. & Towse, J. N. Temporal generalizations in humans: Three further studies. Behav Processes 32, 247–263, doi:10.1016/0376-6357(94)90046-9 (1994).
McCormack, T., Wearden, J. H., Smith, M. C. & Brown, G. D. Episodic temporal generalization: a developmental study. Q J Exp Psychol A 58, 693–704 (2005).
Wearden, J. H. Slowing down an internal clock: Implications for accounts of performance on four timing tasks. The Quarterly Journal of Experimental Psychology 61, 263–274, doi:10.1080/17470210601154610 (2008).
Dixon, P. Models of accuracy in repeated-measures designs. Journal of Memory and Language 59, 447–456 (2008).
Jaeger, T. F. Categorical data analysis: Away from ANOVAs (transformation or not) and towards logit mixed models. Journal of Memory and Language 59, 434–446 (2008).
Brainard, D. H. The Psychophysics Toolbox. Spat Vis 10, 433–436 (1997).
R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria. URL http://www.R-project.org/ (2015).
Hellstrom, A. & Rammsayer, T. H. Time-order errors and standard-position effects in duration discrimination: An experimental study and an analysis by the sensation-weighting model. Atten Percept Psychophys 77, 2409–2423, doi:10.3758/s13414-015-0946-x (2015).
Garcia-Perez, M. A. Does time ever fly or slow down? The difficult interpretation of psychophysical data on time perception. Front Hum Neurosci 8, 415, doi:10.3389/fnhum.2014.00415 (2014).
Bakeman, R. Recommended effect size statistics for repeated measures designs. Behav Res Methods 37, 379–384 (2005).
Hellstrom, A. Time errors and differential sensation weighting. J Exp Psychol Hum Percept Perform 5, 460–477 (1979).
Patching, G. R., Englund, M. P. & Hellstrom, A. Time- and space-order effects in timed discrimination of brightness and size of paired visual stimuli. J Exp Psychol Hum Percept Perform 38, 915–940, doi:10.1037/a0027593 (2012).
Church, R. M. & Gibbon, J. Temporal generalization. J Exp Psychol Anim Behav Process 8, 165–186 (1982).
Dyjas, O., Bausenhart, K. M. & Ulrich, R. Trial-by-trial updating of an internal reference in discrimination tasks: evidence from effects of stimulus order and trial sequence. Atten Percept Psychophys 74, 1819–1841, doi:10.3758/s13414-012-0362-4 (2012).
Dyjas, O. & Ulrich, R. Effects of stimulus order on discrimination processes in comparative and equality judgements: data and models. Q J Exp Psychol (Hove) 67, 1121–1150, doi:10.1080/17470218.2013.847968 (2014).
Bausenhart, K. M., Dyjas, O. & Ulrich, R. Effects of stimulus order on discrimination sensitivity for short and long durations. Attention, Perception, & Psychophysics 77, 1033–1043, doi:10.3758/s13414-015-0875-8 (2015).
Hellstrom, A. Comparison is not just subtraction: effects of time- and space-order on subjective stimulus difference. Percept Psychophys 65, 1161–1177 (2003).
Dyjas, O. & Ulrich, R. Effects of stimulus order on discrimination processes in comparative and equality judgements: Data and models. The Quarterly Journal of Experimental Psychology 67, 1121–1150, doi:10.1080/17470218.2013.847968 (2014).
Rammsayer, T. H. & Troche, S. J. Elucidating the internal structure of psychophysical timing performance in the sub-second and second range by utilizing confirmatory factor analysis. Adv Exp Med Biol 829, 33–47, doi:10.1007/978-1-4939-1782-2_3 (2014).
Hellstrom, A. Sensation weighting in comparison and discrimination of heaviness. J Exp Psychol Hum Percept Perform 26, 6–17 (2000).
Grondin, A. When to start explicit counting in a time-intervals discrimination task: A critical point in the timing process of humans. Journal of Experimental Psychology: Human Perception and Performance 25, 993–1004 (1999).
Wearden, J. H. & Lejeune, H. Scalar properties in human timing: conformity and violations. Q J Exp Psychol (Hove) 61, 569–587 (2008).
Acknowledgements
This work was supported by grants from CONICET, CONICYT/FONDECYT Regular [1130920, 1140114 and 1170010], FONCyT-PICT [2012-0412 and 2012-1309], FONDAP 15150012 and INECO Foundation. The authors thank Marcelo Arlego, Will Harrison and the reviewers for their invaluable contributions.
Author information
Authors and Affiliations
Contributions
Design: E.M., T.B., A.I. Experiment programming: E.M. Data collection: M.S.e., M.B. Data analysis: E.M. Interpretation: E.M., M.S.i., T.B., A.I. Writing: E.M., T.B., M.S.i., A.M.G., A.I. Agreement and approval of the manuscript: E.M., M.S.e., M.B., M.S.i., T.B., A.M.G., A.I.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mikulan, E., Bruzzone, M., Serodio, M. et al. Time-order-errors and duration ranges in the Episodic Temporal Generalization task. Sci Rep 7, 2643 (2017). https://doi.org/10.1038/s41598-017-02386-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-02386-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.