Abstract
From atomic crystals to animal flocks, the emergence of order in nature is captured by the concept of spontaneous symmetry breaking1,2,3,4. However, this cornerstone of physics is challenged when broken symmetry phases are frustrated by geometrical constraints. Such frustration dictates the behaviour of systems as diverse as spin ices5,6,7,8, confined colloidal suspensions9 and crumpled paper sheets10. These systems typically exhibit strongly degenerated and heterogeneous ground states and hence escape the Ginzburg–Landau paradigm of phase ordering. Here, combining experiments, simulations and theory we uncover an unanticipated form of topological order in globally frustrated matter: non-orientable order. We demonstrate this concept by designing globally frustrated metamaterials that spontaneously break a discrete \({{\mathbb{Z}}}_{2}\) symmetry. We observe that their equilibria are necessarily heteregeneous and extensively degenerated. We explain our observations by generalizing the theory of elasticity to non-orientable order-parameter bundles. We show that non-orientable equilibria are extensively degenerated due to the arbitrary location of topologically protected nodes and lines where the order parameter must vanish. We further show that non-orientable order applies more broadly to objects that are non-orientable themselves, such as buckled Möbius strips and Klein bottles. Finally, by applying time-dependent local perturbations to metamaterials with non-orientable order, we engineer topologically protected mechanical memories11,12,13,14,15,16,17,18,19, achieve non-commutative responses and show that they carry an imprint of the braiding of the loads’ trajectories. Beyond mechanics, we envision non-orientability as a robust design principle for metamaterials that can effectively store information across scales, in fields as diverse as colloidal science8, photonics20, magnetism7 and atomic physics21.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All the data supporting this study are available on the public repository https://doi.org/10.5281/zenodo.7689836.
Code availability
All the codes supporting this study are available on the public repository https://doi.org/10.5281/zenodo.7689836.
References
Landau, L. D. On the theory of phase transitions. Zh. Eksp. Teor. Fiz. 7, 19–32 (1937).
Chaikin, P. M. & Lubensky, T. C. Principles of Condensed Matter Physics (Cambridge Univ. Press, 1995).
Toner, J., Tu, Y. & Ramaswamy, S. Hydrodynamics and phases of flocks. Ann. Phys. 318, 170–244 (2005).
Cavagna, A. & Giardina, I. Bird flocks as condensed matter. Annu. Rev. Condens. Matter Phys. 5, 183–207 (2014).
Moessner, R. & Ramirez, A. P. Geometrical frustration. Phys. Today 59, 24–29 (2006).
Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).
Nisoli, C., Moessner, R. & Schiffer, P. Colloquium: Artificial spin ice: designing and imaging magnetic frustration. Rev. Mod. Phys. 85, 1473–1490 (2013).
Ortiz-Ambriz, A., Nisoli, C., Reichhardt, C., Reichhardt, C. J. O. & Tierno, P. Colloquium: ice rule and emergent frustration in particle ice and beyond. Rev. Mod. Phys. 91, 041003 (2019).
Han, Y. et al. Geometric frustration in buckled colloidal monolayers. Nature 456, 898–903 (2008).
Witten, T. A. Stress focusing in elastic sheets. Rev. Mod. Phys. 79, 643–675 (2007).
Treml, B., Gillman, A., Buskohl, P. & Vaia, R. Origami mechanologic. Proc. Natl Acad. Sci. 115, 6916–6921 (2018).
Keim, N. C., Paulsen, J. D., Zeravcic, Z., Sastry, S. & Nagel, S. R. Memory formation in matter. Rev. Mod. Phys. 91, 035002 (2019).
Faber, J. A., Udani, J. P., Riley, K. S., Studart, A. R. & Arrieta, A. F. Dome-patterned metamaterial sheets. Adv. Sci. 7, 2001955 (2020).
Chen, T., Pauly, M. & Reis, P. M. A reprogrammable mechanical metamaterial with stable memory. Nature 589, 386–390 (2021).
Merrigan, C., Nisoli, C. & Shokef, Y. Topologically protected steady cycles in an icelike mechanical metamaterial. Phys. Rev. Res. 3, 023174 (2021).
Jules, T., Reid, A., Daniels, K. E., Mungan, M. & Lechenault, F. Delicate memory structure of origami switches. Phys. Rev. Res. 4, 013128 (2022).
Bense, H. & van Hecke, M. Complex pathways and memory in compressed corrugated sheets. Proc. Natl Acad. Sci. 118, e2111436118 (2021).
Yasuda, H. et al. Mechanical computing. Nature 598, 39–48 (2021).
Melancon, D., Forte, A. E., Kamp, L. M., Gorissen, B. & Bertoldi, K. Inflatable origami: multimodal deformation via multistability. Adv. Funct. Mater. 32, 2201891 (2022).
Bauer, T. et al. Optics. Observation of optical polarization mobius strips. Science 347, 964–966 (2015).
Mazurenko, A. et al. A cold-atom fermi-hubbard antiferromagnet. Nature 545, 462–466 (2017).
Toulouse, G. et al. in Spin Glass Theory and Beyond: An Introduction to the Replica Method and Its Applications Vol. 9, 99–103 (World Scientific, 1987).
Wioland, H., Woodhouse, F. G., Dunkel, J. & Goldstein, R. E. Ferromagnetic and antiferromagnetic order in bacterial vortex lattices. Nat. Phys. 12, 341–345 (2016).
Wu, K.-T. et al. Transition from turbulent to coherent flows in confined three-dimensional active fluids. Science 355, eaal1979 (2017).
Forrow, A., Woodhouse, F. G. & Dunkel, J. Mode selection in compressible active flow networks. Phys. Rev. Lett. 119, 028102 (2017).
Ortiz-Ambriz, A., Nisoli, C., Reichhardt, C., Reichhardt, C. J. O. & Tierno, P. Colloquium: ice rule and emergent frustration in particle ice and beyond. Rev. of Mod. Phys. 91, 041003 (2019).
Molina, A., Kumar, S., Karpitschka, S. & Prakash, M. Droplet tilings for rapid exploration of spatially constrained many-body systems. Proc. Natl Acad. Sci. 118, e2020014118 (2021).
Bertoldi, K., Vitelli, V., Christensen, J. & Van Hecke, M. Flexible mechanical metamaterials. Nat. Rev. Mater. 2, 17066 (2017).
Kang, S. H. et al. Complex ordered patterns in mechanical instability induced geometrically frustrated triangular cellular structures. Phys. Rev. Lett. 112, 098701 (2014).
Celli, P. et al. Shape-morphing architected sheets with non-periodic cut patterns. Soft Matter 14, 9744–9749 (2018).
Meeussen, A. S., Oğuz, E. C., Shokef, Y. & van Hecke, M. Topological defects produce exotic mechanics in complex metamaterials. Nat. Phys. 16, 307–311 (2020).
Deng, B., Yu, S., Forte, A. E., Tournat, V. & Bertoldi, K. Characterization, stability, and application of domain walls in flexible mechanical metamaterials. Proc. Natl Acad. Sci. 117, 31002–31009 (2020).
Coulais, C., Kettenis, C. & van Hecke, M. A characteristic length scale causes anomalous size effects and boundary programmability in mechanical metamaterials. Nat. Phys. 14, 40–44 (2017).
Choi, G. P., Dudte, L. H. & Mahadevan, L. Programming shape using kirigami tessellations. Nat. Mater. 18, 999–1004 (2019).
Zhang, Y., Li, B., Zheng, Q., Genin, G. M. & Chen, C. Programmable and robust static topological solitons in mechanical metamaterials. Nat. Commun. 10, 5605 (2019).
Hatcher, A. Vector Bundles and K-theory https://pi.math.cornell.edu/~hatcher/VBKT/VBpage.html (2017).
Bartolo, D. & Carpentier, D. Topological elasticity of nonorientable ribbons. Phys. Rev. X 9, 041058 (2019).
Bazant, Z. P. & Cedolin, L. Stability of Structures: Elastic, Inelastic, Fracture and Damage Theories (World Scientific, 2010).
Wen, X.-G. Colloquium: zoo of quantum-topological phases of matter. Rev. Mod. Phys. 89, 041004 (2017).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45 (2014).
Guzmán, M., Bartolo, D. & Carpentier, D. Geometry and topology tango in ordered and amorphous chiral matter. SciPost Phys. 12, 038 (2022).
Boas, R. P. Jr Möbius shorts. Math. Mag. 68, 127 (1995).
Fruchart, M., Zhou, Y. & Vitelli, V. Dualities and non-abelian mechanics. Nature 577, 636–640 (2020).
Horowitz, P., Hill, W. & Robinson, I. The Art of Electronics Vol. 2 (Cambridge Univ. Press, 1989).
Zanardi, P. & Rasetti, M. Holonomic quantum computation. Phys. Lett. A 264, 94–99 (1999).
Alicea, J., Oreg, Y., Refael, G., Von Oppen, F. & Fisher, M. P. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 7, 412–417 (2011).
Baker, M. L. et al. A classification of spin frustration in molecular magnets from a physical study of large odd-numbered-metal, odd electron rings. Proc. Natl Acad. Sci. 109, 19113–19118 (2012).
Chardac, A., Hoffmann, L. A., Poupart, Y., Giomi, L. & Bartolo, D. Topology-driven ordering of flocking matter. Phys. Rev. X 11, 031069 (2021).
Cross, M. C. & Hohenberg, P. C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 65, 851–1112 (1993).
Hatcher, A. Algebraic Topology (Cambridge Univ. Press, 2002).
Gramain, A. Topologie des Surfaces (Presses Univ. de France, 1971).
Pesci, A. I., Goldstein, R. E., Alexander, G. P. & Moffatt, H. K. Instability of a möbius strip minimal surface and a link with systolic geometry. Phys. Rev. Lett. 114, 127801 (2015).
Audoly, B. & Pomeau, Y. Elasticity and Geometry: from Hair Curls to the Non-linear Response of Shells (Oxford Univ. Press, 2010).
Acknowledgements
We thank J. van Wezel, M. van Hecke, A. Meeussen, L. Ma and Y. Shokef for insightful discussions and suggestions, D. Giesen for technical assistance, and A. Chardac, C. Jorge and R. Braun for help with the active matter and packing experiments. X.G. acknowledges financial support from the China Scholarship Council. D.B. and D.C. acknowledge support from IDEXLYON ToRe and ANR WTF grants. C.C. acknowledges funding from the European Research Council via the Grant ERC-StG-Coulais-852587-Extr3Me.
Author information
Authors and Affiliations
Contributions
C.C., D.B. and D.C. conceptualized and guided the project. X.G. and C.C. designed the samples and experiments. X.G. and D.B. carried out the experiments. M.G. carried out the numerical simulations. D.B., M.G. and D.C. performed the theoretical study. All authors contributed extensively to the interpretation of the data and the production of the manuscript. D.B. and C.C. wrote the main text. X.G. created the figures and videos. M.G., X.G., D.B. and D.C. wrote the Methods and the Supplementary Information.
Corresponding authors
Ethics declarations
Competing interets
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Guancong Ma and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
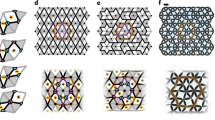
Extended Data Fig. 1 Frustration-induced non-orientability.
a. When deformed under the action of a uniform hydrostatic load, our metaring provide a prototypical example of a broken \({{\mathbb{Z}}}_{2}\) symmetry. The two possible ordered states are labelled by two different colors corresponding to the two wells of the elastic energy. On the sketch of the metaring the color of the arrow corresponds to the sign convention of φ, and the direction of the arrow corresponds to the rotation vector of the lozenges. In a closed metaring, anti-ferromagnetic order is frustrated when the number N of lozenges is odd, as indicated by the dark arrow. b. We can cover the ring of lozenges by two overlapping sets UA (yellow) and UB (blue) where we define two orientations ϵA and ϵB of the staggered angles \({\varphi }_{i}^{\text{A}/\text{B}}\). The global frustration of the anti-ferromagnetic order implies that the transitions functions η1,2 defined as φA = η1,2φB cannot be both equal to 1 in the two overlap sets O1 and O2 (purple). c. Continuum limit. The largest open set over which the elastic-deformation bundle can be trivialized is S1/{s⋆}. At the position s⋆ the non-triviality of the deformation bundle imposes φ(s⋆) = 0.
Extended Data Fig. 2 Orientable vs non-orientable order parameter bundles.
a. A non-orientable order parameter bundle can include non-vanishing field configurations of constant sign. b. Sketch of a non-orientable order parameter bundle and of the local mapping of its total space on \({S}^{1}\times {\mathbb{R}}\).
Extended Data Fig. 3 1D non-orientable phase as connected chiral topological insulators.
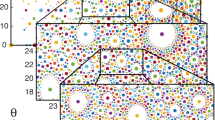
a. Deformation profile of a metaring made of 33 lozenges. The deformation vanishes at a single point (numerical data). b. The spectrum of the dynamical matrix \({\mathcal{D}}\) features an energy gap. However the gap hosts an isolated floppy mode. (The discretized nature of the chain assigns a small negative value to the eigenenergy). c. The floppy mode is located exactly at the position s⋆ where the buckling deformations vanish. d. The chiral polarization field Π computed from the chiral hamiltonian \({\mathcal{H}}\) reveals two singularities: a positive divergence where the buckling deformation vanishes, and a negative divergence at the diametrically opposite position. e. These divergences are the topological signature of localized zero-energy modes. Positive divergence signals the floppy mode captured by the dynamical matrix, whereas the negative divergence signals the presence of a self-stress state, which cannot captured by the dynamics of the chain.
Extended Data Fig. 4 Möbius strips are non-orientable.
a. Ruled surface having the shape of a Möbius strip, and definition of the normal vector n(s). b. It is impossible to define a consistent choice of a continuous normal-vector field on a Möbius strip. Considering two open sets covering the base circle S1, the product of the transition functions over the two open overlaps O1 and O2 is equal to − 1.
Extended Data Fig. 5 Bending-deformation bundle of an elastic Möbius strip.
a. Picture of a buckled Möbius strip described in the Methods. In our simplified picture, the bending elasticity is captured by a single bending angle θ(s), the resulting local displacement vector is \(\delta {{\boldsymbol{R}}}^{\star }(s)=\sin \theta (s){\bf{n}}(s)\). b. Sketch of the line bundle structure. The total space E is locally isomorphic to a cylinder (\({\mathbb{R}}\times {S}^{1}\)) but not globally. The two sections θA and θB are defined on two overlapping open intervals UA and UB of the unit circle S1. c. Maximally large trivial section of the deformation bundle. It is defined over UA = S1\{s⋆}, the non-orientability of the bundle structure implies that the deformation vanishes at s⋆.
Extended Data Fig. 6 Metarings and twisted bands under hydrostatic compression.
From top to bottom, we show pictures of the compressed specimen (top), polar plots of the deformations (middle) and the corresponding order-parameter bundles (bottom). a. Metarings with an even number of pairs of lozenges and twisted bands with an even number of half twists live on a cylinder bundle. The order parameters φ(s) and θ(s) do not vanish under hydrostatic compression. b. Metarings with an odd number of pair of lozenges and twisted bands with an odd number of half twists live on a Möbius bundle. The order parameters φ(s) and θ(s) vanish at one point s⋆ under hydrostatic compression. The inhomogeneous bending angles of twisted bands are due to the inhomogeneous geometry of the bands.
Extended Data Fig. 7 Non-orientable mechanics of toroidal metamaterials.
We vary the parity of the number of lozenges in the toroidal (Nt) and poloidal (Np) directions: a–c. Nt = 26 and Np = 11; d–f. Nt = 27 and Np = 10. (a,d) 3D printed metatori. (b,e) Experimental measurements of the staggered rotation field φ(st, sp) under hydrostatic pressure, and theoretical prediction of the shape of the loop of zero deformation \({\mathcal{L}}\) (solid white line), see also Supplementary Video 4. (c,f) Non-orientable bundles of the staggered-rotation fields. The grey tori represent the base space. The coloured strips illustrate the twist of the bundles along the toroidal and poloidal directions.
Supplementary information
Supplementary Video 1
Active liquid shows global frustration.
Supplementary Video 2
An odd metaring and an even metaring are compressed homogeneously by a vacuum bag.
Supplementary Video 3
A Mobius band and a cylinder are compressed homogeneously by a vacuum bag.
Supplementary Video 4
Tori with different parities of the number of lozenges along toroidal and poloidal directions are compressed homogeneously by a vacuum bag.
Supplementary Video 5
Under two different loading sequences, an odd metaring shows non-commutative response.
Supplementary Video 6
A mechanical sequential logic gate realizes all the set–reset latch operations.
Supplementary Video 7
Numerical simulations of an odd–odd metatorus under different sequences of identical point loads.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Guo, X., Guzmán, M., Carpentier, D. et al. Non-orientable order and non-commutative response in frustrated metamaterials. Nature 618, 506–512 (2023). https://doi.org/10.1038/s41586-023-06022-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-023-06022-7
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.