Main

Milankovitch famously postulated that variations of Earth’s orbit and axis drive climate changes over tens of thousands of years by altering the seasonal cycle of insolation1. By controlling summer temperatures and ice ablation, summer insolation in the northern high latitudes is thought to drive global ice volume changes over glacial–interglacial timescales8. Although modelling studies support this idea9,10, empirical evidence of the specific climate response to insolation changes derives almost entirely from mean annual temperature reconstructions11,12 or from indirect effects on, for example, trapped gases and melt layers in polar ice13,14 and marine aeolian deposits15. The absence of seasonal temperature reconstructions has precluded direct evidence of insolation forcing on seasonal climate, a relationship that may vary geographically. In Antarctica, long records of multiple glacial–interglacial cycles have supported different claims about whether the effects of summer insolation relate most strongly to its maximum intensity, its seasonal integral or to duration above a threshold2,3,16,17. Site-specific empirical determinations would provide valuable tests of such competing ideas.

Seasonal temperature reconstructions

We reconstructed seasonal temperature variability in West Antarctica through the Holocene (the last 11,000 years) and performed model experiments to understand its physical controls. The Holocene offers a window of time for assessing the influence of orbital forcing without the complicating effects of Northern Hemisphere deglaciation18. Our reconstruction (Figs. 1 and 2) uses the high-resolution water-isotope record (δD) from the West Antarctic Ice Sheet (WAIS) Divide ice core (WDC)18,19,20 (Methods—Water isotopes; Extended Data Fig. 1a,b), obtained with a continuous-flow technique that provides millimetre-scale depth resolution21. Layer ages were determined previously2,22.

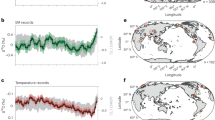
Fig. 1: Water-isotope seasonal variability.
figure 1

a, Example section of the diffusion-corrected (solid line) and raw20 (dashed line) WDC δD records, with annual maxima (red circles) and minima (blue circles) determined algorithmically (Methods—Seasonal water-isotope amplitudes). Extended Data Fig. 1 provides the full high-resolution WDC δD record, diffusion lengths and extrema. b, The 50-yr annual-amplitude averages (summer minus winter divided by 2), with 2σ uncertainty; horizontal line indicates Holocene mean. c–e, The 50-yr δD averages for summer (red, c), mean (purple, d) and winter (blue, e); horizontal line indicates Holocene mean; shaded regions are 2σ bounds for combined analytical and diffusion-correction uncertainty.

Source data

Full size image
Fig. 2: Seasonal temperature reconstruction.
figure 2

a,c, Reconstructed summer and winter temperatures at WDC for 1,000-yr averaging (solid red and blue lines). Shaded regions are 1σ and 2σ uncertainty ranges for combined uncertainties arising from analysis, diffusion correction, seasonality of accumulation, precipitation intermittency, isotope-temperature scaling and reconstructed mean temperatures (Methods—Uncertainties in reconstructing temperatures). Also shown are MEBM-calculated temperatures for 80° S (maximum and minimum annual values) and HadCM3 zonal temperatures for 80° S (late-December for summer, mid-August for winter) (ORBIT, GLAC1D and ICE-6G). The 0 ka ORBIT simulation uses pre-industrial settings, a calculation not available for GLAC1D or ICE-6G. Normalization is done at 1 ka when all model runs intersect within 0.05 °C and the ice-sheet configuration is well known. The ICE-6G values at 11 ka for summer and winter (not shown on plots) are −3.93 °C and −10.82 °C, respectively. Coefficient of determinations for model results versus WDC temperatures (Extended Data Fig. 7) are high for summer (HadCM3 ORBIT R2 = 0.93, P ≪ 0.001; MEBM R2 = 0.80, P ≪ 0.001) but not for winter (HadCM3 ORBIT R2 = 0.00, P = 0.85; MEBM R2 = 0.05, P = 0.30). The winter agreement improves if only the period 0–6 ka is considered (HadCM3 ORBIT R2 = 0.74, P = 0.01; MEBM R2 = 0.39, P = 0.02). b,d, Histograms of net temperature changes over the specified time intervals, derived by Monte Carlo analysis accounting for systematic and non-systematic uncertainties (Methods—Trend analysis). e, WDC mean annual temperature with 1σ and 2σ uncertainty bounds30. Extended Data Table 2 shows the amount of variability in the mean annual temperature that can be explained by the summer and winter temperatures.

Source data

Full size image

Records of seasonal temperatures from ice cores are limited by measurement resolution and information loss from water-isotope diffusion. In Greenland, the longest records separating summer and winter variability extend to only 2 thousand years ago (ka) (refs. 23,24),whereas only climate model simulations are available for older periods10. For Antarctica, before the present study, the longest records spanned only a few centuries25. A combination of three factors accounts for the considerably greater scope of our reconstruction: exceptional depth resolution of measurements, conditions at WAIS Divide (high accumulation, low temperature and thick ice) which allow for preservation of subannual information through the entire Holocene26 and an analysis strategy which circumvents interannual noise by evaluating millennial averages of the seasonal parameters.

Our method corrects water-isotope variations for diffusion26,27,28 and assesses uncertainties including preservation bias and precipitation intermittency (Methods—Diffusion corrections and Uncertainties in reconstructing temperatures). The diffusion correction operates on the high-resolution data and produces isotopic time series from which seasonal summer–winter amplitudes were extracted. These were converted to temperature using a model-derived scaling29 (6.96‰ δD °C−1; Methods—Seasonal temperatures) and added to previously reconstructed annual mean temperatures30 to obtain summer and winter histories.

Seasonal trends

Summer temperatures at WAIS Divide (Fig. 2a) generally rose through the early and middle Holocene, persisted at a maximum between about 5 and 1.5 ka, then decreased toward the present, with a total Holocene range of around 2 °C. These variations broadly correlate with local maximum insolation, rather than with integrated summer insolation or the duration of summer (Fig. 3d,e). Winter temperatures (Fig. 2c) varied less than summer ones overall (about 1 °C range) but also fluctuated at about 10 to 8 ka, a variation too rapid to attribute to orbital forcing.

Fig. 3: Temporal and spatial variability in insolation and model temperatures.
figure 3

a, Insolation change through the Holocene42 for December and January and their average. December best resembles the WDC summer reconstruction. b, The full seasonal cycle of insolation at 80° S for 500-yr snapshots over the Holocene. Line colours in b and c correspond to age. c, Zoom of summer insolation. The maximum always occurs in the latter half of December (grey shading), migrating across 8 days over the course of the Holocene. d, Holocene trends of annual mean insolation (black), annual integrated insolation (dashed red line) and summer-integrated insolation (red line). e, Maximum summer insolation intensity (black line) and summer duration (red lines), defined as the number of days above a threshold insolation value each year. f, Anomaly in maximum insolation coloured by latitude in the Southern Hemisphere. The thick blue line shows the latitude of the WDC site. g, Calculated temperatures for 80° S using the MEBM, including maximum summer value (red), minimum winter value (blue) and amplitude of the seasonal temperature cycle (black).

Source data

Full size image

Annual mean WAIS Divide temperature changes30 (Fig. 2e) were considerably influenced by winter variability in the early Holocene, whereas summer variability dominates the overall Holocene pattern (Methods—Relationship between the annual mean and individual seasons; Extended Data Table 2). Summer variability also accounts for most of the cooling in the last 2 kyr, indicating that the approximately 1 °C annual-average cooling of the entire West Antarctic during this period31,32 likewise reflects this season. Neither season at WDC experienced the early Holocene optimum nor overall Holocene cooling that appears in some global temperature reconstructions33,34. To assess the significance of the dominant multimillennial trends in each season, we performed Monte Carlo analysis (Methods—Trend analysis) using 4 ka as a demarcation point in summer (this is the timing of maximum summer temperature) and 6 ka in winter (when winter temperatures plateau). For summer (Fig. 2b) this indicates a >95% chance that warming from 11 to 4 ka and cooling from 4 ka to present exceeded 0.7 and 0.6 °C, respectively. For winter, the trend from 11 to 6 ka is indistinguishable from zero, whereas cooling of greater than about 0.3 °C from 6 to 0 ka occurred with >95% likelihood (Fig. 2d).

Moist energy balance model

To evaluate how orbitally driven insolation changes may explain the WAIS Divide reconstructed temperatures (Fig. 2), we first simulated temperature history at 80° S using a global, zonal mean (2° resolution) moist energy balance model (MEBM) accounting for incoming and outgoing radiation, albedo and meridional atmospheric-heat transport (Methods—Moist energy balance model). The model is driven by top-of-atmosphere (TOA) seasonal insolation changes (Fig. 3a–e); for this latitude, the maximum summer insolation increases until about 2.5 ka and annual mean and annual- and summer-integrated values mostly decline through the Holocene. The calculations yield summer maximum temperatures and seasonal temperature amplitudes (Fig. 3g) that covary with local maximum summer insolation (Fig. 3e) and with the general pattern of our reconstructed summer temperatures (Extended Data Fig. 7). Although heating at lower latitudes can influence Antarctic temperature through atmospheric and oceanic heat transport, modelled maximum summer temperatures at WAIS Divide correlate best with local insolation (70° to 90° S, R2 = 0.9, P ≪ 0.001 during 0 to 6 ka) rather than insolation anywhere in the subtropical through subpolar latitudes (20° to 60° S, R2 = 0.33–0.55, P < 0.05). Indeed, models indicate heat export from WAIS Divide in summer (Extended Data Fig. 4k), rather than import from more northern locations. Since December is always the month of maximum insolation (Fig. 3a–c), variability of December insolation dominates the response of maximum summer temperature. For winter, modelled temperatures are less variable than those of summer at 80° S (Fig. 3g) because of the lack of direct insolation (Fig. 3b) and have an opposite trend. Winter minima are a function of three factors: changes in the length of the zero-insolation season, the effective cooling rate of the surface and convergent heat transport from lower latitudes. Lower minimum winter temperatures occur at times when the zero-insolation season is longer. However, neither the length of the zero-insolation season, modelled minimum temperatures, nor winter heat divergence correlate well with reconstructed winter temperatures.

HadCM3 simulations

To investigate the role of more-complex geography and mechanisms, including topographical changes not accounted for in the MEBM, we simulated Holocene climate with a fully coupled general circulation model, HadCM3 (ref. 35) (Methods—HadCM3 model simulations). Simulations forced solely by changes in orbital parameters produce summer maximum temperatures (for approximately the December solstice) at 80° S similar to our reconstructed values and to the MEBM: increasing over the Holocene, peaking at 4 to 3 ka and decreasing into the modern era (ORBIT, Fig. 2a). This pattern reflects a strong role of maximum summer insolation in determining observed summer temperatures. The similarity of the early- to mid-Holocene (11–6 ka) summer temperature increase in the orbitally forced HadCM3 simulations and our reconstruction suggests little influence of changing ice-sheet elevation and extent. A similar comparison for winter yields an approximately 1.25 °C decrease of model ORBIT temperature (Fig. 2c) compared to a possible small increase in temperature in the reconstruction (Fig. 2d; >90% chance of >0.1 °C), suggesting some warming resulting from a lowering ice sheet.

Next, as boundary conditions in the HadCM3 simulations, we prescribed variable greenhouse gas (GHG) concentrations and two different ice-sheet histories, GLAC1D and ICE-6G, which entail net surface lowerings of about 83 m and about 208 m, respectively, from 11 to 7 ka at the WDC site (Fig. 4a). These elevation scenarios substantially affect simulated temperatures (Fig. 2a,c). Much of the elevation-induced warming in these models, which occurs primarily in the early Holocene, can be attributed directly to the surface lapse-rate effect (Fig. 4b). However, comparison to the orbital-only runs (Fig. 4c) reveals a remaining temperature anomaly (Fig. 4d), attributable to GHGs, ice-sheet extent and nonlinear responses to simultaneously imposed forcings. Sea ice has only a small impact on the temperature at 80° S in summer (Methods—Sea ice; Extended Data Fig. 6).

Fig. 4: Possible ice elevation histories and the corresponding modelled temperatures.
figure 4

a, Elevation histories used in HadCM3. GLAC1D43 is 96 m higher at 11 ka compared to present and ICE-6G44 is 222 m higher. b, Temperature anomalies from elevation change (GLAC1D, solid lines; ICE-6G, dashed lines) using an atmospheric lapse rate of 9.8 °C km−1 and spatial lapse rates for interior West Antarctica of 12 °C km−1 (ref. 45) and 14 °C km−1 (ref. 46). c, HadCM3 residual-temperature anomalies for December (summer) calculated by subtracting the ORBIT run from the GLAC1D and ICE-6G runs in Fig. 2a, highlighting the portion attributable to changing elevation rather than insolation. d, Residual-temperature change in b subtracted from the results in c, showing the component driven from processes besides the direct lapse-rate (LR) effect and orbital forcing.

Source data

Full size image

Inconsistencies exist between the different ice-sheet scenarios (Fig. 4d) and the summer versus winter seasons but differences are minor enough to permit a bounded estimate of the true Holocene elevation decrease. This calculation is made by comparing the excess of the reconstructed temperature increase over the orbital-only simulation to the same excess for the ice-sheet model simulations and scaling to the elevation changes used in the latter (Methods—Estimating elevation changes). We find central estimates for elevation decrease of 23 m and 53 m from comparison to the GLAC1D and ICE-6G scenarios, respectively, over the period 10 to 3.5 ka (Table 1). Accounting for uncertainties in the seasonal temperature reconstructions (Fig. 2) allows for elevation changes ranging from 33 m increase to 131 m decrease (2σ) from 10 to 3.5 ka or 54 m increase to 162 m decrease (2σ) if the time interval is narrowed to 10 to 6.5 ka (Table 1). Our results, thus, are consistent with geological observations of ice high-stands on mountain nunataks, which indicate less than 100 m of Holocene surface lowering4,5,6.

Table 1 WAIS elevation decrease
Full size table

Winter temperatures on the Antarctic mainland must respond to insolation forcings indirectly, via heat transport from lower latitudes. Orbital forcing models predict winter cooling across the Holocene, mostly from 11 to 6 ka (Figs. 2c and 3g). Both models and reconstructed winter temperatures lack a late Holocene maximum. But in the earlier Holocene, the winter reconstruction does not display the cooling trend expected from models and is dominated by prominent millennial variations. The mismatch with insolation at lower latitudes and absence of local forcings suggests variations in the efficacy of meridional atmospheric-heat transport.

Discussion

Diverse and numerous proxies are used to reconstruct globally averaged surface temperatures for evaluating climate models and distinguishing natural from anthropogenic climate variability33,34,36,37,38. How these proxies depend on seasonal factors has been assessed in only a few cases39. Our West Antarctic study provides a cautionary example, as the mean annual temperature history reflects different controlling factors of summer and winter temperatures whose importance varies with time. In such a situation, important seasonal dynamics may be missed, or proxies misinterpreted, when only mean climate is considered. In addition, incorporating more information from the southern polar regions should help global temperature assessments avoid biases associated with weighting of temperature reconstructions toward northern sites, which have produced differing interpretations of the relationship between global climate and forcings in the Holocene, even including opposing trends34,40,41.

Previous analyses with simplified atmospheric models3 identified the duration of Southern Hemisphere summer as a key driving variable of Antarctic climate at orbital timescales. Some palaeoclimate findings validate this claim; for example, the onset of deglacial warming in West Antarctica corresponds with increasing integrated summer insolation2. Our results—spanning about half a precession cycle—reveal a dominant role for annual maximum insolation in determining West Antarctic summer climate during the Holocene, without precluding a greater role for duration or integrated summer insolation in other periods, such as glacial terminations.

Methods

We measured WAIS Divide core (WDC) water isotopes using continuous-flow analysis (see next section on Water isotopes) and then corrected for cumulative diffusion using spectral techniques to determine diffusion lengths and restore prediffused amplitudes within 140-yr sliding windows (section below on Diffusion corrections; Extended Data Fig. 1c). Summer maxima and winter minima (Fig. 1a) identified in these corrected data were then used to calculate summer and winter amplitudes for each year. We converted the isotope amplitudes to temperature amplitudes using a model-determined scaling factor (section below on Seasonal temperatures) and added them to previously reconstructed mean annual temperatures30 to recover summer and winter values. Substantial seasonal noise processes required multicentennial to millennial averaging to reduce uncertainty (section below on Uncertainties in reconstructing temperatures). To elucidate physical controls on subannual temperatures, we used a simple energy balance model and HadCM3, a general circulation model, to calculate expected changes in seasonal and monthly surface temperatures through time under varying boundary conditions (sections below on Seasonal moist energy balance model and HadCM3 model simulations). Finally, using both observations and modelling, we estimated the change in WAIS surface elevation through the Holocene (section below on Estimating elevation changes).

Water isotopes

WDC water isotopes (Extended Data Fig. 1a) were analysed on a continuous-flow analysis system21 using a Picarro cavity ring-down spectroscopy instrument, model L2130-i. Using permutation entropy47, we identified data anomalies arising from laboratory analysis, which were corrected, including by resampling ice through 1,035.4–1,368.2 m depths (4,517–6,451 yr)48. All other Holocene data are previously published18,31 and available online19,20. Data are reported in 5-mm increments in delta-notation (‰, or per mil) relative to Vienna standard mean ocean water (δ18O = δD = 0‰), normalized to standard light Antarctic precipitation (δ18O = −55.5‰, δD = −428.0‰). WDC is annually dated, with accuracy better than 0.5% of the age between 0 and 12 ka (ref. 22). For the Holocene, the temporal spacing of consecutive 5 mm samples is <0.1 yr and the average <0.05 yr, ranging from about 2.6 weeks at 10 ka to 0.5 week at 1 to 0 ka (ref. 18).

Diffusion corrections

Diffusion in the firn and deeper ice attenuates high-frequency water-isotope information in ice cores26,27,49,50,51,52. Diffusion length quantifies the statistical vertical displacement of water molecules from their original position27,49. We used diffusion-correction code developed by S. Johnsen, University of Copenhagen23,24,27,28, which uses maximum entropy methods to invert an observed power-density spectrum. As an input to these inversions, we determined diffusion lengths (Extended Data Fig. 1c) for 140-yr windows using previous methods18,26. The power-density spectrum observed in the ice-core record \(P\left(f\right)\),after diffusion, is \(P\left(f\right)={P}_{o}\left(f\right){\rm{\exp }}\left[-{\left(2\pi f{\sigma }_{z}\right)}^{2}\right]\), in which \({P}_{o}\left(f\right)\) represents the power spectrum of the undiffused signal (‰2 m−1), \(f\) is the frequency \(\frac{1}{\lambda }\) (1/m), \(\lambda \) the signal wavelength (m), z the depth (m) and \({\sigma }_{z}\) the diffusion length (m). The original, prediffusion power-density spectrum (diffusion-corrected) is calculated as \({P}_{o}\left(f\right)=P\left(f\right){\rm{\exp }}\left(4{\pi }^{2}{f}^{2}{\sigma }_{a}^{2}\right)\), for diffusion length \({\sigma }_{a}\) (yr) and \(f\) now with units of 1/yr. The \({\sigma }_{a}=\frac{{\sigma }_{z}}{{\lambda }_{{\rm{avg}}}}\), in which \({\lambda }_{{\rm{avg}}}\) is the mean annual layer thickness (m yr−1) at a given depth. The diffusion-corrected spectrum takes the form of a series of complex numbers \({X}_{{\rm{R}}}+i{X}_{{\rm{I}}}\) versus \(f\). From this, the amplitude spectrum \(A\) is obtained by \(A\left(f\right)=\sqrt{{X}_{R}^{2}+{X}_{{\rm{I}}}^{2}}\) and the phase spectrum \(\varphi \) is obtained by \(\varphi \left(f\right)={{\rm{\tan }}}^{-1}\left(\frac{{X}_{{\rm{I}}}}{{X}_{{\rm{R}}}}\right)\). The real components of the amplitude and phase spectrums give the diffusion-corrected water-isotope signal \({\delta }_{o}\left(t\right)\) as:

$${\delta }_{o}\left(t\right)=\mathop{\sum }\limits_{i=1}^{N}{A}_{i}{\rm{\cos }}\left(2\pi {f}_{i}t+{\varphi }_{i}\right)$$

Uncertainties on \({\delta }_{o}\left(t\right)\) are determined using the uncertainty range for diffusion lengths26 calculated in each 140-yr window. Before spectral analysis, the isotope data are linearly interpolated at a uniform time interval of 0.05 yr. Our determination of diffusive attenuation and correction arises from the observed frequency spectra themselves and therefore is entirely independent of firn diffusion and densification models.

Seasonal water-isotope amplitudes

To select extrema (summers and winters) in the diffusion-corrected δD signal (Fig. 1a and Extended Data Fig. 1b), we used the ‘findpeaks’ MATLAB function. Figure 1c,e show the resulting time series for summer and winter, averaged with a 50-yr boxcar filter for clarity of trends. For every year defined in the WDC age-scale, we calculated the averaged diffusion-corrected δD. The difference between the two extrema and the mean define the summer and winter isotope amplitudes.

Seasonal temperatures

A linear scaling converted seasonal isotopic amplitudes to seasonal temperature amplitudes, using a sensitivity of isotopes to surface temperatures determined by the simple water-isotope model (SWIM)29. Finally, to find summer and winter temperatures we added the individual seasonal temperature amplitudes to the year’s mean temperature obtained previously30 by calibrating the water-isotope record against borehole temperatures and δ15N constraints on firn thickness.

SWIM is based on earlier numerical Rayleigh-type distillation models53,54, which simulate the transport and distillation of moisture down climatological temperature gradients. As moist air is transported towards the poles and cools, the saturated vapour pressure decreases nonlinearly and moisture above saturation is removed by precipitation. The model keeps track of the isotopic fractionations at each step along this distillation process. In most previous simple models, there is an inconsistency in the calculation of the supersaturation that determines the point of condensation and that drives kinetic isotope fractionation. Modifications to these earlier models, used in SWIM, ensure consistency in the calculation, which results in a smoother relationship between temperature and the δ-values of precipitation and better agreement with observed spatial patterns of δD and δ18O. Given input of both δD and δ18O data, SWIM calculates distributions of source temperatures, the temperature gradients of pseudo-adiabatic pathways and condensation temperature. We used SWIM to derive sensitivities for surface isotope-temperature scalings using diffusion-corrected WDC data to obtain a surface scaling of 6.96‰ δD °C−1. Using raw data, the surface scaling is 7.07‰ δD °C−1. In comparison to other isotope-temperature scalings, ref. 55 obtain about 6.56‰ δD °C−1 and ref. 30 about 7.10‰ δD °C−1 (both converted from δ18O to δD using a factor of 8).

Uncertainties in reconstructing temperatures

We included uncertainties associated with the following factors: measurement analysis, diffusion correction, seasonality of accumulation, precipitation intermittency, modelled isotope-temperature scaling and mean-temperature history. The ‘analysis uncertainty’ is 0.55‰ for δD (1σ) (ref. 21). The ‘diffusion-correction uncertainty’ is described in ref. 26. The uncertainty of the mean-temperature reconstruction, calculated previously30, accounts for most uncertainty in the early Holocene but a small fraction in the late Holocene. Sections ‘Seasonal preservation bias uncertainty’ to ‘Isotope-temperature scaling and associated uncertainty’ below explain the other uncertainty terms. Uncertainties for some factors (analysis and diffusion correction) can be treated as independent random variables so that, on time-averaging, their magnitudes decrease as the inverse of the square root of the number of values. Uncertainties for other factors (intermittency, isotope-temperature scaling, mean temperature and seasonality) might be systematically biased and therefore their magnitudes are taken to be invariant with respect to the interval of averaging. On the basis of the 2σ uncertainties for summer and winter temperature (Fig. 2a,c), we assessed the significance of dominant trends using Monte Carlo analysis (Fig. 2b,d; section on Trend analysis below).

Seasonal preservation bias uncertainty

Unequal seasonal distribution of snowfall could result in different magnitudes of diffusion for winter and summer amplitudes49. The seasonal temperature cycle also affects the magnitude of diffusion for all seasons. We used the Community Firn Model (CFM)56,57, a firn-evolution model with coupled firn temperature, firn densification and water-isotope modules, to test how seasonally weighted accumulation affects the diffusion of specified, hypothetical isotope records progressing from surface snow (δDsnow), to consolidated snowpack in the firn (δDfirn), to solid ice beneath the pore close-off depth (δDice). We applied the back-diffusion calculation (section on Diffusion corrections) to δDice to estimate the original δDsnow. We then assessed how reconstructions of δDsnow could be misinterpreted as a result of different seasonal-accumulation weightings (Extended Data Fig. 2a,b).

We performed five CFM runs using monthly time steps for accumulation, temperature and isotopes (Extended Data Table 1). The seasonal cycle for δDsnow is based on the mean amplitude in Fig. 1b (15.43‰). Five WAIS accumulation scenarios were tested on the basis of monthly accumulation from the regional climate model MAR3.6 (Modèle Atmosphèrique Règional; ERA-Interim forced)58, which spans the period January 1979to December 2017. The mean accumulation over the entire 39-yr period is 0.24745 m ice equivalent yr−1, with about 1.6× as much snow in winter (April to September) as in summer (October to March). The five scenarios are as follows: (1) ‘constant’: identical accumulation for all months (0.0206 m ice equivalent month−1; one-twelfth of the annual mean); (2) ‘cycle’: monthly accumulation equal to MAR monthly means; (3) ‘noise’: using the ‘cycle’ time series, we add noise to each time step in the ‘cycle’ series in the form of a normal random variable of zero mean and the standard deviation for the month from MAR; (4) ‘random’: for each month, the accumulation is a normal random variable with mean and standard deviation equal to MAR monthly values; and (5) ‘loop’: the entire 39-yr MAR accumulation time series is repeated over and over again. For the temperature boundary condition, we used the mean temperature at a height of 2 m for 1979–2017 for each month predicted by MAR to create an annual temperature cycle. We repeated this 12-month time series for the duration of the model runs. This method ensures that model runs, which are designed to test accumulation seasonality, are not affected by interannual temperature variability, while also providing an estimate of the annual temperature cycle, which affects the rate of isotope diffusion in the upper firn.

Extended Data Fig. 2a,b shows the results for the ‘constant’ and ‘cycle’ cases. The diffusion-correction technique accurately reconstructs δDsnow for summer and winter in the ‘constant’ snowfall scenario but underestimates summer values in the MAR ‘cycle’ scenario by about 2.6‰, which is 11% of the full range of the observed WDC summer water-isotope values. Winter values are overestimated by only about 0.6‰, about 3% of the full winter range, since winter has 1.6× as much snow as summer. The ‘noise’, ‘random’ and ‘loop’ runs produce results within 0.3‰. These CFM experiments demonstrate that centennial trends in the summer and winter water isotopes of the order of a few per mil (‰) could arise from large changes in seasonal-accumulation weighting, whereas multimillennial trends ≫2.6‰ are unlikely to be caused by seasonal accumulation and can therefore be interpreted as climate signals of a different origin. For 1,000-yr averaging (as in Fig. 2), HadCM3 indicates seasonal-accumulation weighting (winter:summer) of 1.3 to 1.7 throughout the Holocene (Extended Data Fig. 2f), which yields a 1σ uncertainty of 0.27‰ based on the CFM testing criteria.

To determine observationally if seasonal snowfall changed across the Holocene, we used measured black carbon (BC) concentrations, the only age-scale-independent impurity. BC data are available from 0–2.5 ka and 6–11 ka (ref. 22). Seasonal-fire regimes in South America dominate BC concentrations at WDC, causing BC maxima and minima in autumn and spring, respectively59 (Extended Data Fig. 2c). We split each year into two parts, characterized by rising or falling BC: BC1 and BC2 the depth intervals of rising and falling BC (Extended Data Fig. 2d). The duration of BC2 is longer than BC1 owing to source characteristics59, thus BC1/BC2 < 1 (Extended Data Fig. 2e). The BC1/BC2 ratio can change with time because of variability at the source, changes in atmospheric transport or seasonality of snow deposition. We observe little change in BC1/BC2 resembling the multimillennial trends seen in WDC summers and winters (Extended Data Fig. 2e). Unless there are competing and exactly compensating effects in seasonality (the source change exactly cancels the depositional and transport change or other unlikely scenarios), the BC data provide evidence that changes in WDC seasonal snowfall were not large enough to affect our multimillennial climate interpretations.

Intermittency of precipitation uncertainty

The episodic nature of snowfall creates an incomplete record of local climate variations60, preventing interpretation of trends over short time intervals. We want to interpret isotopic variations averaged over a sufficiently long timescale so that, to within a specified tolerance, trends are not likely to be random noise arising from the spread of distributions preserved in the ice. Using distributions of reconstructed annual amplitudes (Fig. 1b and Extended Data Fig. 2g) for 1,000-yr windows throughout the Holocene, we conducted Monte Carlo resampling simulations to determine that 250-yr averaging-lengths are needed to achieve a standard error of 1‰, corresponding to a mean amplitude-to-noise ratio of 15. For the time period with greatest variability, centred on 4 ka, the standard error for a 1,000-yr average (as used in Fig. 2) is 0.52‰ (Extended Data Fig. 2h). Because this is an amplitude uncertainty (rather than uncertainty associated with a season), we specify the 1σ uncertainties for summer and winter as half of 0.52‰.

Isotope-temperature scaling and associated uncertainty

The conversion of isotopic values (1,000-yr averages) to temperature yields three curves for summer and three for winter: Tnominal, T+1σ and T−1σ. Each curve is normalized to the value at 1 ka (as done in Fig. 2). The difference in the T+1σ and T−1σ curves gives the 1σ uncertainty range +σTscale to −σTscale, which are then added in quadrature to the ref. 30 mean-temperature uncertainties, yielding the final uncertainty estimates shown in Fig. 2.

Relationship between the annual mean and individual seasons

Using 1,000-yr and 300-yr averages of summer, winter and mean temperature (Extended Data Fig. 3c–f), we determined R2 values for summer and winter versus the mean. We then subtracted the 1,000-yr averages from the 300-yr averages to obtain residuals and then determined R2 values again for summer and winter versus the mean (Extended Data Table 2). From 11 to 0 ka, the high summer correlations for the 1,000-yr comparison indicate a strong association of the annual mean temperature with the summer temperature at orbital timescales. At suborbital scales (300–1,000-yr residuals), neither the summer nor the winter alone explain much of the mean annual variability and the annual mean is a random composite of the two seasons. If only 11–7 ka is considered, winter variability explains more of the mean at submillennial scales.

Trend analysis

To assess the significance of dominant trends in our reconstructed seasonal temperatures, we conducted a Monte Carlo analysis founded on the assumption that all possibilities for the unknown time-dependence of errors are equally likely. The essentialmotivation for this approach is that we have determined the magnitudes of uncertainties as a function of age but that we have no information about whether the errors in our reconstruction persist at similar values for long periods of time (exhibit a bias) or whether they fluctuate at high-frequency.

We randomly generated a large number of alternative seasonal temperature histories governed by the uncertainties on 1,000-yr averages (Extended Data Fig. 3a,b), calculated the temperature trends for each alternative history over desired time intervals (such as 11–4 ka and 4–0 ka) and compiled the results into frequency distributions from which probabilities can be calculated (Fig. 2b,d). Specifically, each alternative history deviates from the summer and winter temperature reconstruction by an amount that smoothly varies over time between random nodes whose values are a Gaussian random variable of zero mean and standard deviation for 1,000-yr averages at the age of the node. The number of nodes and the age of each node are random variables, uniformly distributed between 1 and 11 nodes and 0–11 ka, respectively. A small number of nodes produce an alternative temperature history for which the bias is serially correlated for millennia, whereas a large number of nodes produce a history for which the bias is uncorrelated from millennium to millennium.

Seasonal moist energy balance model

We used a simple global, zonal mean MEBM to calculate surface temperatures (Extended Data Fig. 4), accounting for TOA insolation, temperature-dependent longwave emission to space, temperature-dependent albedo to simulate brightening by snow and ice and horizontal atmospheric-heat transport treated as diffusion of near-surface moist static energy61,62,63. The model has a 2° spatial resolution, a single surface and single atmospheric layer and a surface-heat capacity based on the relative fraction of land and ocean surface in the zonal mean. Heat exchange between the surface and atmosphere layers arises from differences in blackbody radiation from each layer and sensible and latent heat exchanges proportional to temperature and specific humidity contrasts (assuming a constant relative humidity of 80%), following bulk aerodynamic formulae. We calculated the annual TOA insolation-cycle at every latitude in 500-yr time slices from 0 to 11 ka. For each time slice the model is run at 2 hour time resolution for 30 model-years to reach equilibrium.

Extended Data Fig. 4 compares the temporal evolution of summer maximum and winter minimum heat divergence by the atmosphere (∇·F) at the WDC site to the summer maximum and winter minimum site temperature and insolation. Although Holocene changes in ∇·F at the WDC site correlate with insolation forcing, the magnitude of changes in maximum direct insolation are much larger than those in atmospheric-heat divergence. Further, the Holocene changes in summertime heat divergence are of the wrong sign to cause net heating at the WDC site (positive divergence is an export of heat by the atmosphere from the site). Heat transport in the Antarctic is convergent in the annual mean but divergent in mid-summer, as intense incoming insolation exceeds longwave emissions from the cold surface.

HadCM3 model simulations

Model setup

We used the fully coupled ocean-atmosphere model HadCM3 (refs. 64,65), v.HadCM3BM2.1, which well simulates tropical Pacific climate and its response to glacial forcing66. Our simulations are snapshots at 1 kyr intervals over the last 11 ka (ref. 35), with time-specific boundary conditions of orbital forcing67, GHG concentration68,69, ice-sheet topography and sea level43,44,70,71,72,73,74. We used three simulations: (1) only orbital forcing changes (ORBIT), with all other boundary conditions set to the pre-industrial; (2) orbital/GHG forcing with GLAC1D ice-sheet elevation history; and (3) orbital/GHG forcing with ICE-6G ice-sheet elevation history. Elevation histories are shown in Fig. 4a. Snapshot simulations were run for at least 500 yr with analysis made on the final 100 yr. Further snapshot simulations for 10 ka allowed us to decompose the role of different forcings, described in the following sections. The large difference in forcings between 10 ka and the pre-industrial late Holocene epoch make this comparison most instructive.

Summer climate

We examined the zonal mean at 80° S in simulations for hypothetical 10 ka worlds, by changing the boundary conditions to compare to the pre-industrial/late Holocene. These simulations are ‘10 ka ORBIT-only’; two runs with only ice sheets at 10 ka and pre-industrial settings otherwise, called ’10 ka GLAC1D-only’ and ‘10 ka ICE-6G-only’; and two runs with all 10 ka forcings, called ‘10 ka GLAC1D-all’ and ‘10 ka ICE-6G-all’. In ‘10 ka ORBIT-only’, reduced TOA shortwave radiation causes a large reduction in shortwave radiation at the surface (SWd) and consequent cooling. Downward longwave radiation (LWd) also decreases, probably because of atmospheric cooling. Sensible heat flux (SHd) to the surface is increased, indicating that the atmosphere and surface do not equally cool; one cause of this is the increased meridional heat convergence (−∇·F).

Changed ice sheets cause summertime cooling in both ‘10 ka GLAC1D-only’ and ‘10 ka ICE-6G-only’, primarily via reduced LWd. Increased SWd, as a result of reduction of depth of the atmospheric column above the ice-sheet surface, counteracts the reduced LWd to some extent. (Reducing the atmospheric column reduces SW absorption and tends to cool the atmosphere, reducing LWd). Both ice-sheet scenarios also cause an increase in −∇·F, partly counteracting summertime cooling.

Using all 10 ka forcings causes cooling through both LWd and SWd. The decrease in SWd is similar in ‘10 ka GLAC1D-all’ and ‘10 ka ICE-6G-all’ and slightly smaller than in ‘10 ka ORBIT-only’, probably because the thinner atmospheric column reduces absorption. The decrease in LWd in ‘10 ka GLAC1D-all’ and ‘10 ka ICE-6G-all’ is larger than in ‘10 ka ORBIT-only’, ‘10 ka GLAC1D-only’ and ‘10 ka ICE-6G-only’. This indicates the importance of feedbacks in the atmosphere. Heat convergence −∇·F increases in both simulations indicating remote feedbacks, in addition to local feedbacks related to the amount of water vapour in the atmosphere.

The preceding description of changes in the zonal mean in the 10 ka simulations compared to pre-industrial period holds for the entire Holocene epoch. Orbital forcing alone reduces SWd and LWd by roughly the same magnitude. With full forcing (including ice sheets), the reduction in LWd is roughly three times the reduction in SWd. Considering an energy budget over the WDC site (79.467° S, 112.085° W), mechanisms are the same as for the zonal mean. Magnitudes of forcings change but reduced SWd still cools the surface, amplified by an LWd feedback dependent on ice-sheet size.

Winter climate

During winter, SWd is no longer a factor as the sun is below the horizon, yet there is still surface warming caused by an increase in LWd. An increase in −∇·F in ‘10 ka ORBIT-only’ warms the atmospheric temperature, increasing LWd and SHd. With an ice sheet imposed, the surface temperature cools. In both ‘10 ka GLAC1D-only’ and ‘10 ka ICE-6G-only’ there is a reduction in −∇·F, reducing LWd and SHd. When all 10 ka forcings are introduced, the change in temperature is smaller than for ice sheet-only runs. In ‘10 ka GLAC1D-all’ we found no change in −∇·F, LWd or surface temperature. This suggests that the increase in −∇·F from orbital forcing is almost perfectly balanced by the change in −∇·F from the ice-sheet configuration.

The processes controlling heat transport over Antarctica are complicated and HadCM3 may not be able to simulate them perfectly. Our simulations indicated that remote processes during winter alter the heat transport, affecting atmospheric and surface temperatures. Raising the topography of Antarctica tends to reduce such heat transport (Extended Data Fig. 5), producing an additional cooling on top of a pure lapse-rate effect75. This cannot, however, explain the prominent millennial-scale changes at about 9.2 and about 7.9 ka (Figs. 1e and 2c). The intricacies of interpreting the early Holocene winter variability in West Antarctica necessitates further study.

Sea ice

Sea ice changes may alter local energy fluxes from the ocean to the atmosphere. In HadCM3, sea ice extent changes across the Holocene. We used two analyses (Extended Data Fig. 6) to show that sea ice is not a primary control on the surface temperature at WDC (80° S): (1) correlation analysis of sea ice changes and surface temperature and (2) atmosphere-only model simulations in which we specified individual changes in the model boundary conditions (including sea ice).

We computed the dominant spatial patterns of sea ice variability using empirical orthogonal functions across all of the HadCM3 simulations (ALL) and individually for three subset simulations (ORBIT, GLAC1D and ICE-6G), from 0 to 11 ka. We projected the model-simulated sea ice for each individual time-slice simulation onto these patterns to compute the amplitude of sea ice variability in each simulation. The amplitude was compared to temperature at 80° S to understand how large-scale changes in the sea ice affect temperature for the months of December (summer) and July (winter) (Extended Data Fig. 6).

In winter, we found negligible correlations between sea ice change and temperature in all sets of simulations (ALL: 0.02; ORBIT: 0.04; GLAC1D: 0.16; ICE-6G: 0.06). This suggests that winter sea ice is not an important factor in determining the temperature at 80° S. In summer, only the ORBIT simulation has meaningful correlations between temperature and sea ice variability (ALL: 0.59; ORBIT: 0.84; GLAC1D: −0.60; ICE-6G: 0.36). The sign of the correlation changes between simulations despite the sea ice change pattern being the same in all simulations. From this we concluded that sea ice is not a dominant control on temperature at 80° S in summer. The correlation in the ORBIT simulations suggests that there may be some relationship between sea ice and temperature; we investigated this with atmosphere-only simulations.

In atmosphere-only simulations at 0 ka and 10 ka, we specified the top of the atmosphere insolation, sea surface temperature (SST) and sea ice from the ORBIT simulations. Over land areas and sea ice regions, the model calculates the surface temperature using the land-surface scheme in the model. The atmosphere model is identical to the model used within the coupled model. We ran a series of experiments varying the orbital configuration, SST or sea ice (summarized in Extended Data Table 3).

The zonal mean of the change in the sea ice that we prescribed can be seen in Extended Data Fig. 6e and the change in the SST can be inferred from Extended Data Fig. 6f–h. Extended Data Fig. 6f shows that the atmosphere-only model replicates the change in temperature of the coupled model. Extended Data Fig. 6g shows that the effect of the 10 ka orbital configuration (‘Atmos_10k_insol’) is to cool Antarctica considerably by about 0.5 °C. North of 65° S there is no change in the surface temperature, primarily a response to the imposed SST and sea ice, which are the same in the ‘Control’ and ‘Atmos_10k_insol’. Imposing the SST and sea ice from 10 ka (‘Atmos_10k_ice_SST’), we find very little change in the surface temperature over Antarctica but there are some large changes in the surface temperature north of 70° S. Extended Data Fig. 6h shows the result of imposing 10 ka SST or 10 ka sea ice. The 10 ka SST (‘Atmos_10k_SST’) tends to warm Antarctica, consistent with the large increases in SST north of 65° S. Changing sea ice (‘Atmos_10k_ice’) tends to cool Antarctica. Both effects are small, approximately 0.1 °C and of opposite sign. This explains the small net change in the surface-temperature change over Antarctica when SST and sea ice are changed simultaneously, as shown by ‘Atmos_10k_SST_ice’. It should be noted that in the coupled system a change in sea ice cannot be decoupled from a change in the SST, so not only is the effect of sea ice on the climate small, it is also probably associated with a compensating change in SST. From these simulations we concluded that sea ice and SST changes are not a dominant driver of the change in the surface temperature over Antarctica.

Extended Data Fig. 6e shows that the change in sea ice at 10 ka in ORBIT is much larger than the change in either GLAC1D or ICE-6G. The ORBIT simulations do not account for all of the changes in the boundary conditions at 10 ka and are therefore less realistic than either ICE-6G or GLAC1D. Because ICE-6G and GLAC1D both show much smaller changes in the sea ice and SST than ORBIT, we expect that in reality there is also a much smaller change in the sea ice and SST than in ORBIT. We thus concluded that sea ice has a small impact on the temperature at 80° S in summer.

We also performed a similar analysis of the winter season (not shown). We found that the atmosphere-only model does not compare well with the coupled model, simulating very little change in the surface temperature. Doing a term-by-term decomposition of the atmosphere model is not, therefore, particularly useful as it tells us more about the model rather than the physical climate. The failure of the atmosphere-only model to capture the changes at 10 ka suggests that the importance of the SST and sea ice is in their day-to-day coupling with the atmosphere and not in any long-term mean change in this season.

Estimating elevation changes

Temperatures simulated by HadCM3 for ORBIT provide a control scenario against which observations can be compared to identify the signal of elevation change. For a chosen time interval, the net reconstructed warming ΔTR exceeds that of ORBIT by an amount ΔTR − ΔTO. This can be compared to the effective lapse rate (ΔTM − ΔTO)/ΔZM defined by a HadCM3 simulation including topographic change (GLAC1D or ICE-6G models) and all forcings, for model warming ΔTM and model elevation decrease ΔZM. Specifically, the estimated elevation decrease is ΔZR = ΔZM((ΔTR − ΔTO)/(ΔTM − ΔTO)). Summer and winter reconstructions offer two separate assessments, for which we calculate the algebraic average.

Accounting for uncertainties in ΔTR requires recognizing that uncertainties of summer and winter reconstructions are not independent, while also recognizing that they emerge from two independent sources: uncertainty in the mean annual temperature history (calculated in ref. 30) and uncertainty in the seasonal amplitude (calculated in the present study). In general, the uncertainty of seasonal temperature at a specified time is the quadrature sum of annual and amplitude uncertainties, which gives 1σ and 2σ uncertainties for a given season and time. However, if the true value of annual temperature is shifted by an amount ασ from the nominal reconstruction, this must be true for both summer and winter. And if the true value of amplitude is shifted by an amount βσ from the nominal reconstruction, the temperature shift must be +βσ in one season but −βσ in the other.

To define bounding cases on elevation change in a specified time interval, we calculated the maximal (or minimal) temperature change ΔTR for a season by differencing the upper (or lower) limit at one end of the interval with the lower (or upper) limit at the other end and also calculating the corresponding ΔTR for the opposite season required by the correlated errors. The elevation decreases ΔZR were then calculated by comparison to HadCM3 simulations, as specified previously and the summer and winter values averaged. This process was completed four times for each time interval and HadCM3 model, corresponding to four different initial ΔTR (maximum and minimum ΔTR for summer and maximum and minimum ΔTR for winter) and the most extreme case taken as the result (this proved to be the one starting with maximum summer ΔTR). Table 1 lists results for two time intervals and the two HadCM3 simulations with variable topography.