Abstract
The standard model of particle physics1,2,3,4 describes the known fundamental particles and forces that make up our Universe, with the exception of gravity. One of the central features of the standard model is a field that permeates all of space and interacts with fundamental particles5,6,7,8,9. The quantum excitation of this field, known as the Higgs field, manifests itself as the Higgs boson, the only fundamental particle with no spin. In 2012, a particle with properties consistent with the Higgs boson of the standard model was observed by the ATLAS and CMS experiments at the Large Hadron Collider at CERN10,11. Since then, more than 30 times as many Higgs bosons have been recorded by the ATLAS experiment, enabling much more precise measurements and new tests of the theory. Here, on the basis of this larger dataset, we combine an unprecedented number of production and decay processes of the Higgs boson to scrutinize its interactions with elementary particles. Interactions with gluons, photons, and W and Z bosons—the carriers of the strong, electromagnetic and weak forces—are studied in detail. Interactions with three third-generation matter particles (bottom (b) and top (t) quarks, and tau leptons (τ)) are well measured and indications of interactions with a second-generation particle (muons, μ) are emerging. These tests reveal that the Higgs boson discovered ten years ago is remarkably consistent with the predictions of the theory and provide stringent constraints on many models of new phenomena beyond the standard model.
Similar content being viewed by others
Main
The standard model of particle physics has been tested by many experiments since its formulation1,2,3,4 and, after accounting for the neutrino masses, no discrepancies between experimental observations and its predictions have been established so far. A central feature of the standard model is the existence of a spinless quantum field that permeates the Universe and gives mass to massive elementary particles. Testing the existence and properties of this field and its associated particle, the Higgs boson, has been one of the main goals of particle physics for several decades. In the standard model, the strength of the interaction, or ‘coupling’, between the Higgs boson and a given particle is fully defined by the particle’s mass and type. There is no direct coupling to the massless standard model force mediators, the photons and gluons, whereas there are three types of couplings to massive particles in the theory. The first is the ‘gauge’ coupling of the Higgs boson to the mediators of the weak force, the W and Z vector bosons. Demonstrating the existence of gauge couplings is an essential test of the spontaneous electroweak symmetry-breaking mechanism5,6,7,8,9. The second type of coupling involves another fundamental interaction, the Yukawa interaction, between the Higgs boson and matter particles, or fermions. The third type of coupling is the ‘self-coupling’ of the Higgs boson to itself. A central prediction of the theory is that the couplings scale with the particle masses and they are all precisely predicted once all the particle masses are known. The experimental determination of the couplings of the Higgs boson to each individual particle therefore provides important and independent tests of the standard model. It also provides stringent constraints on theories beyond the standard model, which generally predict different patterns of coupling values.
In 2012, the ATLAS12 and CMS13 experiments at the Large Hadron Collider (LHC)14 at CERN announced the discovery of a new particle with properties consistent with those predicted for the Higgs boson of the standard model10,11. More precise measurements that used all of the proton–proton collision data taken during the first data-taking period from 2011 to 2012 at the LHC (Run 1) showed evidence that, in contrast to all other known fundamental particles, the properties of the discovered particle were consistent with the hypothesis that it has no spin15,16. Alternate spin-1 and spin-2 hypotheses were also tested and were excluded at a high level of confidence. Investigations of the charge conjugation and parity (CP) properties of the new particle were also performed, demonstrating consistency with the CP-even quantum state predicted by the standard model, while still allowing for small admixtures of non-standard model CP-even or CP-odd states15,16. Limits on the particle’s lifetime were obtained through indirect measurements of its natural width15,16,17,18,19. In addition, more precise measurements of the new particle’s interactions with other elementary particles were achieved20. The results of all these investigations demonstrated that its properties were compatible with those of the standard model Higgs boson. However, the statistical uncertainties associated with these early measurements allowed considerable room for possible interpretations of the data in terms of new phenomena beyond the standard model and left many predictions of the standard model untested.
The characterization of the Higgs boson continued during the Run 2 data-taking period between 2015 and 2018. About 9 million Higgs bosons are predicted to have been produced in the ATLAS detector during this period, of which only about 0.3% are experimentally accessible. This is 30 times more events than at the time of its discovery, owing to the higher rate of collisions and the increase of the collision energy from 8 teraelectronvolts (TeV) to 13 TeV, which raises the production rate. In this Article, the full Run 2 dataset, corresponding to an integrated luminosity of 139 inverse femtobarns (fb−1), is used for the measurements of Higgs boson production and decay rates, which are used to study the couplings between the Higgs boson and the particles involved. This improves on the previous measurements obtained with partial Run 2 datasets21,22. The corresponding predictions depend on the value of the Higgs boson mass, which has now been measured by the ATLAS and CMS experiments23,24,25 with an uncertainty of approximately 0.1%. The predictions employed in this article use the combined central value of 125.09 GeV23.
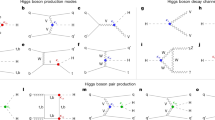
The dominant production process at the LHC, which accounts for about 87% of Higgs boson production, is the heavy-quark loop-mediated gluon–gluon fusion process (ggF). The second most copious process is vector boson fusion (VBF), in which two weak bosons, either Z or W bosons, fuse to produce a Higgs boson (7%). Next in rate is production of a Higgs boson in association with a weak (V = W, Z) boson (4%). Production of a Higgs boson in association with a pair of top quarks \((t\bar{t}H)\) or bottom quarks \((b\bar{b}H)\) each account for about 1% of the total rate. The contribution of other \(q\bar{q}H\) processes is much smaller and experimentally not accessible. Only about 0.05% of Higgs bosons are produced in association with a single top quark (tH). Representative Feynman diagrams of these processes are shown in Fig. 1a–e. After it is produced, the Higgs boson is predicted to decay almost instantly, with a lifetime of 1.6 × 10−22 seconds. More than 90% of these decays are via eight decay modes (Fig. 1f–i): decays into gauge boson pairs, that is, W bosons with a probability, or branching fraction, of 22%, Z bosons 3%, photons (γ) 0.2%, Z boson and photon 0.2%, as well as decays into fermion pairs, that is, b quarks 58%, c quarks 3%, τ leptons 6%, and muons (μ) 0.02%. There may also be decays of the Higgs boson into invisible particles, above the standard model prediction of 0.1%, which are also searched for. Such decays are possible in theories beyond the standard model, postulating, for example, the existence of dark matter particles that do not interact with the detector.
a–e, The Higgs boson is produced via gluon–gluon fusion (a), vector boson fusion (VBF; b) and associated production with vector bosons (c), top or b quark pairs (d), or a single top quark (e). f–i, The Higgs boson decays into a pair of vector bosons (f), a pair of photons or a Z boson and a photon (g), a pair of quarks (h), and a pair of charged leptons (i). Loop-induced Higgs boson interactions with gluons or photons are shown in blue, and processes involving couplings to W or Z bosons in green, to quarks in orange, and to leptons in red. Two different shades of green (orange) are used to separate the VBF and VH (\(t\bar{t}H\) and tH) production processes.
In this Article, the mutually exclusive measurements of Higgs boson production and decays probing all processes listed above are combined, taking into account the correlations among their uncertainties. In a single measurement, different couplings generally contribute in the production and decay. The combination of all measurements is therefore necessary to constrain these couplings individually. This enables key tests of the Higgs sector of the standard model to be performed, including the determination of the coupling strengths of the Higgs boson to various fundamental particles and a comprehensive study of the kinematic properties of Higgs boson production. The latter could reveal new phenomena beyond the standard model that are not observable through measurements of the coupling strengths.
The ATLAS detector at the LHC
The ATLAS experiment12 at the LHC is a multipurpose particle detector with a forward–backward symmetric, cylindrical geometry and a near 4π coverage in solid angle. The detector records digitized signals produced by the products of LHC’s proton bunch collisions, hereafter termed collision ‘events’. It is designed to identify a wide variety of particles and measure their momenta and energies. These particles include electrons, muons, τ leptons and photons, as well as gluons and quarks, which produce collimated jets of particles in the detector. Because the jets from b quarks and c quarks contain hadrons with relatively long lifetimes, they can be identified by observing a decay vertex, which typically occurs at a measurable distance from the collision point. The presence of particles that do not interact with the detector, such as neutrinos, can be inferred by summing the vector momenta of the visible particles in the plane transverse to the beam and imposing conservation of transverse momenta.
The detector components closest to the collision point measure charged-particle trajectories and momenta. This inner spectrometer is surrounded by calorimeters that are used in the identification of particles and in the measurement of their energies. The calorimeters are in turn surrounded by an outer spectrometer dedicated to measuring the trajectories and momenta of muons, the only charged particle to travel through the calorimeters. A two-level trigger system was optimized for Run 2 data-taking26 to select events of interest at a rate of about 1 kHz from the proton bunch collisions occurring at a rate of 40 MHz. An extensive software suite27 is used in the simulation, reconstruction and analysis of real and simulated data, in detector operations, and in the trigger and data-acquisition systems of the experiment.
Input measurements and combination procedure
Physics analyses typically focus on particular production and decay processes and measure the number of Higgs boson candidates observed after accounting for non-Higgs background processes. To determine the strengths of the interactions of the Higgs boson, simultaneous fits with different physically motivated assumptions are performed on a combined set of complementary measurements. The relative weights of the input measurements in the combination depend on the analysis selection efficiencies, on the signal rates associated with the Higgs processes studied by the analysis, on the signal-to-background ratios, and on the associated systematic uncertainties.
For each decay mode entering the combination, the production process is assessed via event classification based on the properties of particles produced in association with the Higgs boson, mostly via dedicated machine-learning approaches. Unless stated otherwise, studies of each decay mode consider all individual or combined contributions from six production processes: ggF, VBF, WH, ZH, \(t\bar{t}H\) and tH. Higgs boson interactions are further explored via additional event classification of each production process based on the kinematic properties of the produced Higgs boson and the associated particles.
The input to the combined measurement includes the latest results from the decay modes that initially led to the Higgs boson discovery: H → ZZ → ℓ+ℓ−ℓ+ℓ− decays28 with two Z bosons that subsequently decay into a pair of oppositely charged electrons or muons; H → W ±W∓ → ℓ±νℓℓ∓νℓ decays targeting separately the ggF and VBF29, and WH and ZH30 production processes; and H → γγ decays31 with two high-energy photons. The latter is the only measurement used to discriminate between the \(t\bar{t}H\) and tH processes. These diboson decay modes are for the first time complemented by a search for the rare H → Zγ → ℓ+ℓ−γ decay32. The decays of Higgs bosons to fermions are also extensively explored. The measurement of the dominant \(H\to b\bar{b}\) decay mode is particularly challenging owing to a very large multi-jet background, which can be suppressed by requiring the presence of additional particles characteristic of the WH or ZH33,34, VBF35 and \(t\bar{t}H\)36 production processes. As a new input, the fully hadronic \(H\to b\bar{b}\) signal events with large Higgs boson transverse momentum are also considered37, providing for the first time sensitivity to the ggF production process in this decay mode. The sensitivity of the latest measurement in the H → τ+τ− decay mode38 is now extended to the VH and combined \(t\bar{t}H\) and tH production processes. In addition to the \(t\bar{t}H\) measurements obtained in the γγ, τ+τ− and ZZ decay modes, a complementary analysis that is sensitive to τ+τ−, \({W}^{\pm }{W}^{\mp }\) and ZZ decays is performed using events with multiple leptons in the final state39. The considerably more challenging measurements of Higgs boson couplings to second-generation fermions are explored via searches for the H → μ+μ− decay40 and, included in the combination for the first time, \(H\to c\bar{c}\) decay41. Owing to the large multi-jet background, the latter decay mode is currently accessed only via WH and ZH production. Finally, the inputs to the combination are complemented by the latest direct searches in the VBF and ZH production processes for Higgs boson decays into invisible particles that escape the detector42,43. A summary of these input measurements used in the combination is available in Extended Data Table 1.
All input measurements are performed with the full set of Run 2 data, except for the measurements of previous works30,39, which use a partial Run 2 dataset collected during 2015 and 2016. The direct searches for invisible Higgs boson decays and the \(H\to c\bar{c}\) measurements are employed only for measurements of the relevant Higgs boson coupling strengths, and the \(H\to b\bar{b}\) measurements at high Higgs boson transverse momenta37 are considered only when probing the kinematic properties of Higgs boson production. All other inputs are used for the measurements of production cross-sections, branching fractions and coupling strengths. The measurement of kinematic properties of Higgs boson production excludes input measurements from previous works30,32,39,40,41, owing to their limited sensitivity.
Analyses performed with the Run 2 data introduce a number of improvements, often resulting in up to 50% better signal sensitivities compared to those expected from just the increase in the analysed amount of data. These improvements include better particle reconstruction (optimized to cope with an increased number of proton interactions per bunch crossing), dedicated reconstruction of highly Lorentz-boosted \(H\to b\bar{b}\) decays, a greater number of simulated events, higher granularity of the kinematic regions that are probed in each production process, and improved signal and background theory predictions.
The standard model is tested by comparing the observed signal rates to theory predictions that require state-of-the-art calculations of Higgs boson production cross-sections and branching fractions44,45,46,47,48,49,50. All signal reconstruction efficiencies and most background rates are predicted from the simulation. The simulation is complemented by the use of dedicated signal-depleted control data for measurements of selected background processes and to constrain signal-selection efficiencies. A common set of event generators were used in all analyses to describe the gluon and quark interactions in the proton–proton collisions. The generated particles were passed through a detailed simulation of the ATLAS detector response prior to their reconstruction and identification.
The statistical analysis of the data is described in more detail in Methods. It relies on a likelihood formalism, where the product of the likelihood functions describing each of the input measurements is calculated in order to obtain a combined likelihood51. The effects of experimental and theoretical systematic uncertainties on the predicted signal and background yields are implemented by including nuisance parameters in the likelihood function. The values of those additional parameters are either fully determined by the included data, or constrained by Gaussian terms that multiply the likelihood. The effects of uncertainties that affect multiple measurements are propagated coherently through the fit by using common nuisance parameters.
The statistical test of a given signal hypothesis, used for the measurement of the parameters of interest, is performed with a test statistic that is based on the profile likelihood ratio52. The confidence intervals of the measured parameters and the p value used to test the compatibility of the results and the standard model predictions are constructed from the test statistic distribution, which is obtained using asymptotic formulae52.
The total uncertainty in the measurement of a given parameter of interest can be decomposed into different components. The statistical uncertainty is obtained from a fit with all externally constrained nuisance parameters set to their best-fit values. The systematic uncertainty, the squared value of which is evaluated as the difference between the squares of the total uncertainty and the statistical uncertainty, can be decomposed into categories by setting all relevant subsets of nuisance parameters to their best-fit values.
Combined measurement with ATLAS Run 2 data
The Higgs boson production rates are probed by the likelihood fit to observed signal yields described earlier. Because the production cross-section σi and the branching fraction Bf for a specific production process i and decay mode f cannot be measured separately without further assumptions, the observed signal yield for a given process is expressed in terms of a single signal strength modifier \({\mu }_{if}=({\sigma }_{i}/{\sigma }_{i}^{{\rm{SM}}})({B}_{f}/{B}_{f}^{{\rm{SM}}})\), where the superscript ‘SM’ denotes the corresponding standard model prediction. Assuming that all production and decay processes scale with the same global signal strength μ = μif, the inclusive Higgs boson production rate relative to the standard model prediction is measured to be
The total measurement uncertainty is decomposed into components for statistical uncertainties, experimental systematic uncertainties, and theory uncertainties in both signal and background modelling. Both the experimental and the theoretical uncertainties are almost a factor of two lower than in the Run 1 result20. The presented measurement supersedes the previous ATLAS combination with a partial Run 2 dataset22, decreasing the latest total measurement uncertainty by about 30%.
Higgs boson production is also studied per individual process. As opposed to the top quark decay products from \(t\bar{t}H\) production, the identification efficiency of b jets from the \(b\bar{b}H\) production is low, making the \(b\bar{b}H\) process experimentally indistinguishable from ggF production. The \(b\bar{b}H\) and ggF processes are therefore grouped together, with \(b\bar{b}H\) contributing a relatively small amount: of the order of 1% to the total \({\rm{g}}{\rm{g}}{\rm{F}}+b\bar{b}H\) production. In cases where several processes are combined, the combination assumes the relative fractions of the components to be those from the standard model within corresponding theory uncertainties. Results are obtained from the fit to the data, where the cross-section of each production process is a free parameter of the fit. Higgs boson decay branching fractions are set to their standard model values, within the uncertainties specified previously44. The results are shown in Fig. 2a.
a, Cross-sections for different Higgs boson production processes are measured assuming standard model (SM) values for the decay branching fractions. b, Branching fractions for different Higgs boson decay modes are measured assuming SM values for the production cross-sections. The lower panels show the ratios of the measured values to their SM predictions. The vertical bar on each point denotes the 68% confidence interval. The p value for compatibility of the measurement and the SM prediction is 65% for a and 56% for b. Data are from ATLAS Run 2.
All measurement results are compatible with the standard model predictions. For the ggF and VBF production processes, which were previously observed in Run 1 data, the cross-sections are measured with a precision of 7% and 12%, respectively. The following production processes are now also observed: WH with an observed (expected) signal significance of 5.8 (5.1) standard deviations (σ), ZH with 5.0σ (5.5σ) and the combined \(t\bar{t}H\) and tH production processes with 6.4σ (6.6σ), where the expected signal significances are obtained under the standard model hypothesis. The separate \(t\bar{t}H\) and tH measurements lead to an observed (expected) upper limit on tH production of 15 (7) times the standard model prediction at the 95% confidence level (CL), with a relatively large negative correlation coefficient of 56% between the two measurements. This is due to cross-contamination between the \(t\bar{t}H\) and tH processes in the set of reconstructed events that provide the highest sensitivity to these production processes.
Branching fractions of individual Higgs boson decay modes are measured by setting the cross-sections for Higgs boson production processes to their respective standard model values. The results are shown in Fig. 2b. The branching fractions of the γγ, ZZ, \({W}^{\pm }{W}^{\mp }\) and τ+τ− decays, which were already observed in the Run 1 data, are measured with a precision ranging from 10% to 12%. The \(b\bar{b}\) decay mode is observed with a signal significance of 7.0σ (expected 7.7σ), and the observed (expected) signal significances for the H → μ+μ− and H → Zγ decays are 2.0σ (1.7σ) and 2.3σ (1.1σ), respectively.
The assumptions about the relative contributions of different decay or production processes in the above measurements are relaxed by directly measuring the product of production cross-section and branching fraction for different combinations of production and decay processes. The corresponding results are shown in Fig. 3. The measurements are in agreement with the standard model prediction.
The horizontal bar on each point denotes the 68% confidence interval. The narrow grey bands indicate the theory uncertainties in the standard model (SM) cross-section multiplied by the branching fraction predictions. The p value for compatibility of the measurement and the SM prediction is 72%. σi Bf is normalized to the SM prediction. Data are from ATLAS Run 2.
To determine the value of a particular Higgs boson coupling strength, a simultaneous fit of many individual production times branching fraction measurements is required. The coupling fit presented here is performed within the κ framework53 with a set of parameters κ that affect the Higgs boson coupling strengths without altering any kinematic distributions of a given process.
Within this framework, the cross-section times the branching fraction for an individual measurement is parameterized in terms of the multiplicative coupling strength modifiers κ. A coupling strength modifier κp for a production or decay process via the coupling to a given particle p is defined as \({\kappa }_{p}^{2}={\sigma }_{p}/{\sigma }_{p}^{{\rm{SM}}}\) or \({\kappa }_{p}^{2}={\varGamma }_{p}/{\varGamma }_{p}^{{\rm{SM}}}\), respectively, where Γp is the partial decay width into a pair of particles p. The parameterization takes into account that the total decay width depends on all decay modes included in the present measurements, as well as currently undetected or invisible, direct or indirect decays predicted by the standard model (such as those to gluons, light quarks or neutrinos) and the hypothetical decays into non-standard model particles. The decays to non-standard model particles are divided into decays to invisible particles and other decays that would be undetected owing to large backgrounds. The corresponding branching fractions for the two are denoted by Binv. and Bu., respectively.
In the following, three classes of models with progressively fewer assumptions about coupling strength modifiers are considered. Standard model values are assumed for the coupling strength modifiers of first-generation fermions, and the modifiers of the second-generation quarks are set to those of the third generation, except where κc is left free-floating in the fit. Owing to their small sizes, these couplings are not expected to noticeably affect any of the results. The ggF production and the H → γγ and H → Zγ decays are loop-induced processes. They are either expressed in terms of the more fundamental coupling strength scale factors corresponding to the particles that contribute to the loop-induced processes in the standard model, or treated using effective coupling strength modifiers κg, κγ and κZγ, respectively. The latter scenario accounts for possible loop contributions from particles beyond the standard model. The small contribution from the loop-induced gg → ZH process is always parameterized in terms of the couplings to the corresponding standard model particles.
The first model tests one scale factor for the vector bosons, κV = κW = κZ, and a second, κF, which applies to all fermions. In general, the standard model prediction of κV = κF = 1 does not hold in extensions of the standard model. For example, the values of κV and κF would be less than 1 in models in which the Higgs boson is a composite particle. The effective couplings corresponding to the ggF, H → γγ and H → Zγ loop-induced processes are parameterized in terms of the fundamental standard model couplings. It is assumed that there are no invisible or undetected Higgs boson decays beyond the standard model, that is, Binv. = Bu. = 0. As only the relative sign between κV and κF is physical and a negative relative sign has been excluded with a high level of confidence20, κV ≥ 0 and κF ≥ 0 are assumed. Figure 4 shows the results of a combined fit in the (κV, κF) plane. The best-fit values and their uncertainties from the combined fit are κV = 1.035 ± 0.031 and κF = 0.95 ± 0.05, compatible with the standard model predictions. A relatively large positive correlation of 39% is observed between the two fit parameters, because some of the most sensitive input measurements involve the ggF production process (that is, via couplings to fermions) with subsequent Higgs boson decays into vector bosons.
In the second class of models, the coupling strength modifiers for W, Z, t, b, c, τ and μ are treated independently. All modifiers are assumed to be positive. It is assumed that only standard model particles contribute to the loop-induced processes, and modifications of the fermion and vector boson couplings are propagated through the loop calculations. Invisible or undetected non-standard model Higgs boson decays are not considered. These models enable testing of the predicted scaling of the couplings of the Higgs boson to the standard model particles as a function of their mass using the reduced coupling strength modifiers \(\sqrt{{\kappa }_{V}{g}_{V}/2{\rm{vev}}}=\sqrt{{\kappa }_{V}}({m}_{V}/{\rm{vev}})\) for weak bosons with a mass mV and κFgF = κFmF/vev for fermions with a mass mF, where gV and gF are the corresponding absolute coupling strengths and ‘vev’ is the vacuum expectation value of the Higgs field. Figure 5 shows the results for two scenarios: one with the coupling to c quarks constrained by κc = κt in order to cope with the low sensitivity to this coupling; and the other with κc left as a free parameter in the fit. All measured coupling strength modifiers are found to be compatible with their standard model prediction. When the coupling strength modifier κc is left unconstrained in the fit, an upper limit of κc < 5.7 (7.6) times the standard model prediction is observed (expected) at 95% CL and the uncertainty in each of the other parameters increases because of the resulting weaker constraint on the total decay width. This improves the current observed (expected) limit of κc < 8.5 (12.4) at 95% CL from the individual measurement of \(H\to c\bar{c}\) decays41 despite the relaxed assumptions on other coupling strength modifiers, through constraints coming from the parameterization of the total Higgs boson decay width that impacts all measurements.
They are defined as κFmF/vev for fermions (F = t, b, τ, μ) and \(\sqrt{{\kappa }_{V}}{m}_{V}/{\rm{vev}}\) for vector bosons as a function of their masses mF and mV. Two fit scenarios with κc = κt (coloured circle markers), or κc left free-floating in the fit (grey cross markers) are shown. Loop-induced processes are assumed to have the standard model (SM) structure, and Higgs boson decays to non-SM particles are not allowed. The vertical bar on each point denotes the 68% confidence interval. The p values for compatibility of the combined measurement and the SM prediction are 56% and 65% for the respective scenarios. The lower panel shows the values of the coupling strength modifiers. The grey arrow points in the direction of the best-fit value and the corresponding grey uncertainty bar extends beyond the lower panel range. Data are from ATLAS Run 2.
The third class of models in the κ framework closely follows the previous one, but allows for the presence of non-standard model particles in the loop-induced processes. These processes are parameterized by the effective coupling strength modifiers κg, κγ and κZγ instead of propagating modifications of the standard model particle couplings through the loop calculations. It is also assumed that any potential effect beyond the standard model does not substantially affect the kinematic properties of the Higgs boson decay products. The fit results for the scenario in which invisible or undetected non-standard model Higgs boson decays are assumed not to contribute to the total Higgs decay width, that is, Binv. = Bu. = 0, are shown in Fig. 6 together with the results for the scenario allowing such decays. To avoid degenerate solutions, the latter constrains Bu. ≥ 0 and imposes the additional constraint κV ≤ 1 that naturally arises in various scenarios of physics beyond the standard model54,55. All measured coupling strength modifiers are compatible with their standard model predictions.
The horizontal bars on each point denote the 68% confidence interval. The scenario in which Binv. = Bu. = 0 is assumed is shown as solid lines with circle markers. The p value for compatibility with the standard model (SM) prediction is 61% in this case. The scenario in which Binv. and Bu. are allowed to contribute to the total Higgs boson decay width while assuming that κV ≤ 1 and Bu. ≥ 0 is shown as dashed lines with square markers. The lower panel shows the 95% CL upper limits on Binv. and Bu.. Data are from ATLAS Run 2.
When allowing invisible or undetected non-standard model Higgs boson decays to contribute to the total Higgs boson decay width, the previously measured coupling strength modifiers do not change significantly, and upper limits of Bu. < 0.12 (expected 0.21) and Binv. < 0.13 (expected 0.08) are set at 95% CL on the corresponding branching fraction. The latter improves on the current best limit of Binv. < 0.145 (expected 0.103) from direct ATLAS searches42.
In all tested scenarios, the statistical and the systematic uncertainty contribute almost equally to the total uncertainty in most of the κ parameter measurements. The exceptions are the κμ, κZγ, κc and Bu. measurements, for which the statistical uncertainty still dominates.
Kinematic properties of Higgs boson production probing the internal structure of its couplings are studied in the framework of simplified template cross-sections44,56,57,58. The framework partitions the phase space of standard model Higgs boson production processes into a set of regions defined by the specific kinematic properties of the Higgs boson and, where relevant, of the associated jets, W bosons, or Z bosons, as described in Methods. The regions are defined so as to provide experimental sensitivity to deviations from the standard model predictions, to avoid large theory uncertainties in these predictions, and to minimize the model-dependence of their extrapolations to the experimentally accessible signal regions. Signal cross-sections measured in each of the introduced kinematic regions are compared with those predicted when assuming that the branching fractions and kinematic properties of the Higgs boson decay are described by the standard model.
The results of the simultaneous measurement in 36 kinematic regions are presented in Fig. 7. Compared to previous results with a smaller dataset22, a much larger number of regions are probed, particularly at high Higgs boson transverse momenta, where in many cases the sensitivity to new phenomena beyond the standard model is expected to be enhanced. All measurements are consistent with the standard model predictions.
The vertical bar on each point denotes the 68% confidence interval. The p value for compatibility of the combined measurement and the standard model (SM) prediction is 94%. Kinematic regions are defined separately for each production process, based on the jet multiplicity, the transverse momentum of the Higgs \(({p}_{{\rm{T}}}^{H})\) and vector bosons (\({p}_{{\rm{T}}}^{W}\) and \({p}_{{\rm{T}}}^{Z}\)) and the two-jet invariant mass (mjj). The ‘VH-enriched’ and ‘VBF-enriched’ regions with the respective requirements of \({m}_{jj}\in [60,120)\,{\rm{GeV}}\) and \({m}_{jj}\notin [60,120)\,{\rm{GeV}}\) are enhanced in signal events from VH and VBF productions, respectively. Data are from ATLAS Run 2.
Conclusion
In summary, the production and decay rates of the Higgs boson were measured using the dataset collected by the ATLAS experiment during Run 2 of the LHC from 2015 to 2018. The measurement results were found to be in excellent agreement with the predictions of the standard model. In different scenarios, the couplings to the three heaviest fermions, the top quark, the b quark and the τ lepton, were measured with uncertainties ranging from about 7% to 12% and the couplings to the weak bosons (Z and W) were measured with uncertainties of about 5%. In addition, indications are emerging of the presence of very rare Higgs boson decays into second-generation fermions and into a Z boson and a photon. Finally, a comprehensive study of Higgs boson production kinematics was performed and the results were also found to be compatible with standard model predictions. In the ten years since its discovery, the Higgs boson has undergone many experimental tests that have demonstrated that, so far, its nature is remarkably consistent with the predictions of the standard model. However, some of its key properties—such as the coupling of the Higgs boson to itself—remain to be measured. In addition, some of its rare decay modes have not yet been observed and there is ample room for new phenomena beyond the standard model to be discovered. Substantial progress on these fronts is expected in the future, given that detector upgrades are planned for the coming years, that systematic uncertainties are expected to be reduced considerably59, and that the size of the LHC’s dataset is projected to increase by a factor of 20.
Methods
Experimental set-up
The ATLAS detector12 consists of an inner tracking detector surrounded by a thin superconducting solenoid, electromagnetic and hadron calorimeters, and a muon spectrometer incorporating three large superconducting air-core toroidal magnets.
ATLAS uses a right-handed coordinate system with its origin at the nominal interaction point in the centre of the detector and the z axis along the beam pipe. The x axis points from the interaction point to the centre of the LHC ring, and the y axis points upwards. Cylindrical coordinates (r, ϕ) are used in the transverse plane, ϕ being the azimuthal angle around the z axis. The pseudorapidity is defined in terms of the polar angle θ as η = −ln(tan(θ/2)).
The inner-detector (ID) system is immersed in a 2-T axial magnetic field and provides charged-particle tracking in the range |η| < 2.5. The high-granularity silicon pixel detector covers the vertex region and typically provides four measurements per track, the first hit normally being in the insertable B-layer (IBL) installed before Run 260,61. It is followed by the silicon microstrip tracker (SCT), which usually provides eight measurements per track. These silicon detectors are complemented by the transition radiation tracker (TRT), which enables radially extended track reconstruction up to |η| < 2.0. The TRT also provides electron identification information based on the fraction of hits (typically 30 in total) above a higher energy-deposit threshold corresponding to transition radiation.
The calorimeter system covers the pseudorapidity range |η| < 4.9. Within the region |η| < 3.2, electromagnetic calorimetry is provided by barrel and endcap high-granularity lead/liquid-argon (LAr) calorimeters, with an additional thin LAr presampler covering |η| < 1.8 to correct for energy loss in material upstream of the calorimeters. Hadron calorimetry is provided by the steel/scintillator-tile calorimeter, segmented into three barrel structures within |η| < 1.7, and two copper/LAr hadron endcap calorimeters. The solid angle coverage is completed with forward copper/LAr and tungsten/LAr calorimeter modules optimized for electromagnetic and hadronic energy measurements, respectively.
The muon spectrometer (MS) comprises separate trigger and high-precision tracking chambers measuring the deflection of muons in a magnetic field generated by the superconducting air-core toroidal magnets. The field integral of the toroids ranges between 2.0 and 6.0 Tm across most of the detector. Three layers of precision chambers, each consisting of layers of monitored drift tubes, covers the region |η| < 2.7, complemented by cathode-strip chambers in the forward region, where the background is highest. The muon trigger system covers the range |η| < 2.4 with resistive-plate chambers in the barrel, and thin-gap chambers in the endcap regions.
The performance of the vertex and track reconstruction in the inner detector, the calorimeter resolution in electromagnetic and hadronic calorimeters and the muon momentum resolution provided by the muon spectrometer are given previously12.
Interesting events are selected by the first-level trigger system implemented in custom hardware, followed by selections made by algorithms implemented in software in the high-level trigger62. The first-level trigger accepts events from the 40-MHz bunch crossings at a rate below 100 kHz, which the high-level trigger further reduces in order to record events to disk at about 1 kHz.
Statistical framework
The results of the combination presented in this paper are obtained from a likelihood function defined as the product of the likelihoods of each input measurement. The observed yield in each category of reconstructed events follows a Poisson distribution the parameter of which is the sum of the expected signal and background contributions. The number of signal events in any category k is split into the different production and decay modes:
where the sum indexed by i runs either over the production processes (ggF, VBF, WH, ZH, \(t\bar{t}H\), tH) or over the set of the measured production kinematic regions, and the sum indexed by f runs over the decay final states (ZZ, WW, γγ, Zγ, \(b\bar{b}\), \(c\bar{c}\), τ+τ−, μ+μ−). The quantity \({ {\mathcal L} }_{k}\) is the integrated luminosity of the dataset used in category k, and \({(A\epsilon )}_{if}^{k}\) is the acceptance times selection efficiency factor for production process i and decay mode f in category k. Acceptances and efficiencies are obtained from the simulation (corrected by calibration measurements in control data for the efficiencies). Their values are subject to variations due to experimental and theoretical systematic uncertainties. The cross-sections σi and branching fractions Bf are the parameters of interest of the model. Depending on the model being tested, they are either free parameters, set to their standard model prediction or parameterized as functions of other parameters. All cross-sections are defined in the Higgs boson rapidity range |yH| < 2.5, which is related to the polar angle of the Higgs boson’s momentum in the detector and corresponds approximately to the region of experimental sensitivity.
The impact of experimental and theoretical systematic uncertainties on the predicted signal and background yields is taken into account by nuisance parameters included in the likelihood function. The predicted signal yields from each production process, the branching fractions and the signal acceptance in each analysis category are affected by theory uncertainties. The combined likelihood function is therefore expressed as:
where nk,b, \({n}_{k,b}^{{\rm{signal}}}\) and \({n}_{k,b}^{{\rm{bkg}}}\) stand for the number of observed events, the number of expected signal events and the number of expected background events in bin b of analysis category k, respectively. The parameters of interest are noted α, the nuisance parameters are θ, P represents the Poisson distribution, and G stands for Gaussian constraint terms assigned to the nuisance parameters. Some nuisance parameters are meant to be determined by data alone and do not have any associated constraint term. This is, for instance, the case for background normalization factors that are fitted in control categories. The effects of nuisance parameters affecting the normalizations of signal and backgrounds in a given category are generally implemented using the multiplicative expression:
where n0 is the nominal expected yield of either signal or background and σ the value of the uncertainty. This ensures that n(θ) > 0 even for negative values of θ. For the majority of nuisance parameters, including all those affecting the shapes of the distributions, a linear expression is used instead on each bin of the distributions:
The systematic uncertainties are broken down into independent underlying sources, so that when a source affects multiple or all analyses the associated nuisance parameter can be fully correlated across the terms in the likelihood corresponding to these analyses by using common nuisance parameters. This is the case of systematic uncertainties in the luminosity measurement63, in the reconstruction and selection efficiencies64,65,66,67,68,69,70 and in the calibrations of the energy measurements71,72,73,74. Their effects are propagated coherently by using common nuisance parameters whenever applicable. Only a few components of the systematic uncertainties are correlated between the analyses performed using the full Run 2 data and those using only the 2015 and 2016 data, owing to differences in their assessment, in the reconstruction algorithms and in software releases. Systematic uncertainties associated with the modelling of background processes, as well as uncertainties due to the limited number of simulated events used to estimate the expected signal and background yields, are treated as being uncorrelated between analyses.
Uncertainties in the parton distribution functions are implemented coherently in all input measurements and all analysis categories75. Uncertainties in modelling the parton showering into jets of particles affect the signal acceptances and efficiencies, and are common to all input measurements within a given production process. Similarly, uncertainties due to missing higher-order quantum chromodynamics (QCD) corrections are common to a given production process. Their implementation in the kinematic regions of the simplified template cross-sections framework results in a total of 66 uncertainty sources, where overall acceptance effects are separated from migrations between the various bins (for example, between jet multiplicity regions or between dijet invariant mass regions)76. Both the acceptance and signal yield uncertainties affect the signal strength modifier and coupling strength modifier results, which rely on comparisons of measured and expected yields. Only acceptance uncertainties affect the cross-section and branching fraction results. The uncertainties in the Higgs boson branching fractions due to dependencies on standard model parameter values (such as b and c quark masses) and missing higher-order effects are implemented using the correlation model described previously44.
In total, over 2,600 sources of systematic uncertainty are included in the combined likelihood. For most of the presented measurements, the systematic uncertainty is expected to be of similar size or somewhat smaller than the corresponding statistical uncertainty. The systematic uncertainties are dominant for the parameters that are measured the most precisely, that is, the global signal strength and the production cross-sections for the ggF and VBF processes. The expected systematic uncertainty of the global signal strength measurement (about 5%) is larger than the statistical uncertainty (3%), with similar contributions from the theory uncertainties in signal (4%) and background modelling (1.7%), and from the experimental systematic uncertainty (3%). The latter is predominantly composed of the uncertainty in the luminosity measurement (1.7%), followed by the uncertainties in electron, jet and b-jet reconstruction, data-driven background modelling, as well as from the limited number of simulated events (about 1% each). All other sources of experimental uncertainty combined contribute an additional 1%. The systematic uncertainty in the production cross-section of the ggF process is dominated by experimental uncertainties (3.5%) followed by signal theory uncertainties (3%), compared to a statistical uncertainty of 4%. For the VBF process, where the statistical uncertainty is 8%, the experimental uncertainties are estimated to be 5%, and the signal theory uncertainties add up to 7%. Systematic uncertainties are also dominant over the statistical uncertainties in the measurements of the branching fractions into W pairs and τ lepton pairs.
Measurements of the parameters of interest use a statistical test based on the profile likelihood ratio52:
where α are the parameters of interest and θ are the nuisance parameters. The \(\hat{\hat{{\boldsymbol{\theta }}}}({\boldsymbol{\alpha }})\) notation indicates that the nuisance parameters values are those that maximize the likelihood for given values of the parameters of interest. In the denominator, both the parameters of interest and the nuisance parameters are set to the values (\(\hat{{\boldsymbol{\alpha }}}\), \(\hat{{\boldsymbol{\theta }}}\)) that unconditionally maximize the likelihood. The estimates of the parameters α are these values \(\hat{{\boldsymbol{\alpha }}}\) that maximize the likelihood ratio.
Owing to the usually large number of events selected in the measurements, all results presented in this paper are obtained in the asymptotic regime where the likelihood approximately follows a Gaussian distribution. It was checked in previous iterations of the individual input measurements, for instance ref. 77, that this assumption also holds in cases with low event counts by comparing the results of the asymptotic formulae with those of pseudo-experiments. This confirmed the results from a previous work52 that the Gaussian approximation becomes valid for as few as ≳5 background events. In the asymptotic regime twice the negative logarithm of the profile likelihood λ(α) = −2ln(Λ(α)) follows a χ2 distribution with a number of degrees of freedom equal to the number of parameters of interest. Confidence intervals for a given confidence level (CL), usually 68%, are then defined as the regions fulfilling \(\lambda ({\boldsymbol{\alpha }}) < {F}_{n}^{-1}({\rm{C}}{\rm{L}})\) where \({F}_{n}^{-1}\) is the quantile function of the χ2 distribution with n degrees of freedom, so \({F}_{1}^{-1}=1\,(4)\) for a 1σ (2σ) CL with one degree of freedom. The values of the parameters α corresponding to these confidence intervals are obtained by scanning the profile likelihood. Similarly, the p value pSM = 1 − Fn(λ(αSM)) is used to test the compatibility of the measurement and the standard model prediction. The correlations between the parameters are estimated by inverting the matrix of the second derivatives of the likelihood.
The expected significances and limits are determined using the ‘Asimov’ datasets52, which are obtained by setting the observed yields to their expected values when the nuisance parameters are set to the values that maximize the likelihood \(\hat{{\rm{\theta }}}\).
Parameterization within the κ framework
Within the κ framework, the cross-section for an individual measurement is parameterized as
where Γf is the partial width for a Higgs boson decay to the final state f and ΓH is the total decay width of the Higgs boson. The total width is given by the sum of the partial widths of all the decay modes included. Contributions to the total Higgs boson decay width owing to phenomena beyond the standard model may manifest themselves as a value of coupling strength modifier κp differing from one, or a value of Binv. or Bu. differing from zero. The Higgs boson total width is then expressed as \({\varGamma }_{H}({\boldsymbol{\kappa }},{B}_{{\rm{inv.}}},{B}_{{\rm{u.}}})={\kappa }_{H}^{2}({\boldsymbol{\kappa }},{B}_{{\rm{inv.}}},{B}_{{\rm{u.}}}){\varGamma }_{H}^{{\rm{SM}}}\) with
Higgs boson production cross-sections and partial and total decay widths are parameterized in terms of the coupling strength modifiers as shown in table 9 of ref. 22. An improved parameterization including additional sub-leading contributions is used in this paper to match the increased precision of the measurements.
Kinematic regions probing Higgs boson production
The definitions of kinematic regions for the precision study of Higgs boson production in the framework of simplified template cross-sections44,56,57,58 are based on the predicted properties of particles generated in a given production process. The partitioning follows the so-called Stage-1.2 scheme, which features a slightly finer granularity than the Stage-1.1 scheme57 and introduces the Higgs boson transverse momentum categories for the \(t\bar{t}H\) production process. Higgs bosons are required to be produced with rapidity |yH| < 2.5. Associated jets of particles are constructed from all stable particles with a lifetime greater than 10 ps, excluding the decay products of the Higgs boson and leptons from W and Z boson decays, using the anti-kt algorithm78 with a jet radius parameter R = 0.4, and must have a transverse momentum pT,jet > 30 GeV. Standard model predictions are assumed for the kinematic properties of Higgs boson decays. Phenomena beyond the standard model can substantially modify these properties, and thus the acceptance of the signal, especially for the WW or ZZ decay modes, and this should be considered when using these measurements for the relevant interpretations.
Higgs boson production is first classified according to the nature of the initial state and the associated particles, the latter including the decay products of W and Z bosons if they are present. These classes are: \(t\bar{t}H\) and tH processes; qq′ → Hqq′ processes, with contributions from both VBF and quark-initiated VH (where V = W, Z) production with a hadronic decay of the vector boson; pp → VH production with a leptonic decay of the vector boson (V(ℓℓ, ℓν)H), including gg → ZH → ℓℓH production; and finally the ggF process combined with \(gg\to ZH\to q\bar{q}H\) production to form a single gg → H process. The contribution of the \(b\bar{b}H\) production process is taken into account as a 1%44 increase of the gg → H yield in each kinematic region, because the acceptances for both processes are similar for all input analyses44.
The input measurements in individual decay modes provide only limited sensitivity to the cross-section in some of the regions of the Stage-1.2 scheme, mainly because of the small number of events in some of these regions. In other cases, they only provide sensitivity to a combination of these regions, leading to strongly correlated measurements. To mitigate these effects, some of the Stage-1.2 kinematic regions were merged for the combined measurement.
Compared to individual input measurements, systematic theory uncertainties associated with the signal predictions have been updated for the combination to closely follow the granularity of the Stage-1.2 scheme. The QCD scale uncertainties in ggF production were updated for all input channels that are sensitive to this production process. Out of 18 uncertainty sources in total, two account for overall fixed-order and resummation effects, two cover the migrations between different jet multiplicity bins, seven are associated with the modelling of the Higgs boson transverse momentum (\({p}_{{\rm{T}}}^{H}\)) in different phase-space regions, four account for the uncertainty in the distribution of the dijet invariant mass (mjj) variable, one covers the modelling of the Higgs boson plus two leading jets transverse momentum (\({p}_{{\rm{T}}}^{Hjj}\)) distribution in the ≥2-jet region, one pertains to modelling of the distribution of the Higgs boson plus one jet transverse momentum (\({p}_{{\rm{T}}}^{Hj}\)) divided by \({p}_{{\rm{T}}}^{H}\) in the high-\({p}_{{\rm{T}}}^{H}\) region, and finally, the last takes into account the uncertainty from the choice of top quark mass scheme. Theory uncertainties for the qq′ → Hqq′ and \(t\bar{t}H\) processes are defined previously28, and those of the V(ℓℓ, ℓν)H kinematic region follow the scheme described in an earlier work76. For the kinematic regions defined by the merging of several Stage-1.2 regions, the signal acceptance factors are determined assuming that the relative fractions in each Stage-1.2 region are given by their standard model values, and the uncertainties predicted by the standard model in these fractions are taken into account.
Data availability
The experimental data that support the findings of this study are available in HEPData with the identifier https://doi.org/10.17182/hepdata.130266.
Code availability
The ATLAS data reduction software is available at the following link: https://zenodo.org/record/4772550. Statistical modelling and analysis is based on the ROOT software and its embedded RooFit and RooStats modules, available at https://zenodo.org/record/3895852. Code to configure these statistical tools and to process their output is available upon request.
Change history
06 December 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41586-022-05581-5
18 October 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41586-023-06248-5
References
Weinberg, S. A model of leptons. Phys. Rev. Lett. 19, 1264–1266 (1967).
Glashow, S. L. Partial symmetries of weak interactions. Nucl. Phys. 22, 579–588 (1961).
Salam, A. Weak and electromagnetic interactions. Proc. 8th Nobel Symposium, Conf. Proc. C 680519, 367–377 (1968).
’t Hooft, G. & Veltman, M. J. G. Regularization and renormalization of gauge fields. Nucl. Phys. B 44, 189–213 (1972).
Higgs, P. W. Broken symmetries, massless particles and gauge fields. Phys. Lett. 12, 132–133 (1964).
Higgs, P. W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 13, 508–509 (1964).
Englert, F. & Brout, R. Broken symmetry and the mass of gauge vector mesons. Phys. Rev. Lett. 13, 321–323 (1964).
Guralnik, G., Hagen, C. & Kibble, T. Global conservation laws and massless particles. Phys. Rev. Lett. 13, 585–587 (1964).
Kibble, T. Symmetry breaking in non-Abelian gauge theories. Phys. Rev. 155, 1554–1561 (1967).
ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012).
CMS Collaboration. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–60 (2012).
ATLAS Collaboration. The ATLAS experiment at the CERN Large Hadron Collider. J. Instrum. 3, S08003 (2008).
CMS Collaboration. The CMS experiment at the CERN LHC. J. Instrum. 3, S08004 (2008).
Evans, L. & Bryant, P. LHC Machine. J. Instrum. 3, S08001 (2008).
ATLAS Collaboration. Study of the spin and parity of the Higgs boson in diboson decays with the ATLAS detector. Eur. Phys. J. C 75, 476 (2015).
CMS Collaboration. Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV. Phys. Rev. D 92, 012004 (2015).
ATLAS Collaboration. Constraints on the off-shell Higgs boson signal strength in the high-mass ZZ and WW final states with the ATLAS detector. Eur. Phys. J. C 75, 335 (2015).
CMS Collaboration. Search for Higgs boson off-shell production in proton–proton collisions at 7 and 8 TeV and derivation of constraints on its total decay width. J. High Energy Phys. 2016-09, 51 (2016).
CMS Collaboration. Limits on the Higgs boson lifetime and width from its decay to four charged leptons. Phys. Rev. D 92, 072010 (2015).
ATLAS Collaboration & CMS Collaboration. Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at √s = 7 and 8 TeV. J. High Energy Phys. 2016-08, 45 (2016).
CMS Collaboration. Combined measurements of Higgs boson couplings in proton–proton collisions at √s = 13 TeV. Eur. Phys. J. C 79, 421 (2019).
ATLAS Collaboration. Combined measurements of Higgs boson production and decay using up to 80 fb−1 of proton–proton collision data at √s = 13 TeV collected with the ATLAS experiment. Phys. Rev. D 101, 012002 (2020).
ATLAS Collaboration & CMS Collaboration. Combined measurement of the Higgs boson mass in pp collisions at √s = 7 and 8 TeV with the ATLAS and CMS experiments. Phys. Rev. Lett. 114, 191803 (2015).
ATLAS Collaboration. Measurement of the Higgs boson mass in the H → ZZ* → 4ℓ and H → γγ channels with √s = 13 TeV pp collisions using the ATLAS detector. Phys. Lett. B 784, 345–366 (2018).
CMS Collaboration. A measurement of the Higgs boson mass in the diphoton decay channel. Phys. Lett. B 805, 135425 (2020).
ATLAS Collaboration. Operation of the ATLAS trigger system in Run 2. J. Instrum. 15, P10004 (2020).
ATLAS Collaboration. The ATLAS Collaboration Software and Firmware Report No. ATL-SOFT-PUB-2021-001 (CERN, 2021); https://cds.cern.ch/record/2767187
ATLAS Collaboration. Higgs boson production cross-section measurements and their EFT interpretation in the 4ℓ decay channel at √s = 13 TeV with the ATLAS detector. Eur. Phys. J. C 80, 957 (2020); erratum 81, 398 (2021).
ATLAS Collaboration. Measurements of Gluon Fusion and Vector-Boson-Fusion Production of the Higgs Boson in H → WW* → eνμν Decays using pp Collisions at √s = 13 TeV with the ATLAS Detector Report No. CERN-EP-2022-078 (CERN, 2022).
ATLAS Collaboration. Measurement of the production cross section for a Higgs boson in association with a vector boson in the H → WW* → ℓνℓν channel in pp collisions at √s = 13 TeV with the ATLAS detector. Phys. Lett. B 798, 134949 (2019).
ATLAS Collaboration. Measurement of the Properties of Higgs Boson Production at √s = 13 TeV in the H → γγ Channel using 139 fb−1 of pp Collision Data with the ATLAS Experiment Report No. CERN-EP-2022-094 (CERN, 2022).
ATLAS Collaboration. A search for the Zγ decay mode of the Higgs boson in pp collisions at √s = 13 TeV with the ATLAS detector. Phys. Lett. B 809, 135754 (2020).
ATLAS Collaboration. Measurements of WH and ZH production in the \(H\to b\bar{b}\) decay channel in pp collisions at 13 TeV with the ATLAS detector. Eur. Phys. J. C 81, 178 (2021).
ATLAS Collaboration. Measurement of the associated production of a Higgs boson decaying into b quarks with a vector boson at high transverse momentum in pp collisions at √s = 13 TeV with the ATLAS detector. Phys. Lett. B 816, 136204 (2021).
ATLAS Collaboration. Measurements of Higgs bosons decaying to bottom quarks from vector boson fusion production with the ATLAS experiment at √s = 13 TeV. Eur. Phys. J. C 81, 537 (2020).
ATLAS Collaboration. Measurement of Higgs boson decay into b-quarks in associated production with a top-quark pair in pp collisions at √s = 13 TeV with the ATLAS detector. Preprint at https://arxiv.org/abs/2111.06712 (2021).
ATLAS Collaboration. Constraints on Higgs boson production with large transverse momentum using \(H\to b\bar{b}\) decays in the ATLAS detector. Phys. Rev. D 105, 092003 (2022).
ATLAS Collaboration. Measurements of Higgs boson production cross-sections in the H → τ+τ− decay channel in pp collisions at √s = 13 TeV with the ATLAS detector. Preprint at https://arxiv.org/abs/2201.08269 (2022).
ATLAS Collaboration. Evidence for the associated production of the Higgs boson and a top quark pair with the ATLAS detector. Phys. Rev. D 97, 072003 (2018).
ATLAS Collaboration. A search for the dimuon decay of the Standard Model Higgs boson with the ATLAS detector. Phys. Lett. B 812, 135980 (2021).
ATLAS Collaboration. Direct constraint on the Higgs–charm coupling from a search for Higgs boson decays into charm quarks with the ATLAS detector. Preprint at https://arxiv.org/abs/2201.11428 (2022).
ATLAS Collaboration. Search for invisible Higgs boson decays in events with vector-boson fusion signatures using 139 fb−1 of proton–proton data recorded by the ATLAS experiment. Preprint at https://arxiv.org/abs/2202.07953 (2022).
ATLAS Collaboration. Search for associated production of a Z boson with an invisibly decaying Higgs boson or dark matter candidates at √s = 13 TeV with the ATLAS detector. Phys. Lett. B 829, 137066 (2022).
LHC Higgs Cross Section Working Group, de Florian, D. et al. Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector Report No. CERN-2017-002 (CERN, 2017); https://doi.org/10.23731/CYRM-2017-002
Kudashkin, K., Lindert, J. M., Melnikov, K. & Wever, C. Higgs bosons with large transverse momentum at the LHC. Phys. Lett. B 782, 210–214 (2018).
Djouadi, A., Kalinowski, J., Mühlleitner, M. & Spira, M. HDECAY: twenty++ years after. Comput. Phys. Commun. 238, 214–231 (2019).
Bonetti, M., Melnikov, K. & Tancredi, L. Higher order corrections to mixed QCD-EW contributions to Higgs boson production in gluon fusion. Phys. Rev. D 97, 056017 (2018).
Dulat, F., Lazopoulos, A. & Mistlberger, B. iHixs 2 – inclusive Higgs cross sections. Comput. Phys. Commun. 233, 243–260 (2018).
Harlander, R. V., Klappert, J., Liebler, S. & Simon, L. vh@nnlo-v2: new physics in Higgs Strahlung. J. High Energy Phys. 2018-05, 89 (2018).
Cacciari, M., Dreyer, F. A., Karlberg, A., Salam, G. P. & Zanderighi, G. Fully differential vector-boson-fusion Higgs production at next-to-next-to-leading order. Phys. Rev. Lett. 115, 082002 (2015).
ATLAS and CMS Collaborations & The LHC Higgs Combination Group. Procedure for the LHC Higgs Boson Search Combination in Summer 2011 Report No. ATL-PHYS-PUB-2011-011 (CERN, 2011); https://cds.cern.ch/record/1375842
Cowan, G., Cranmer, K., Gross, E. & Vitells, O. Asymptotic formulae for likelihood-based tests of new physics. Eur. Phys. J. C 71, 1554 (2011); erratum 73, 2501 (2013).
LHC Higgs Cross Section Working Group, Heinemeyer, S. et al. Handbook of LHC Higgs Cross Sections: 3. Higgs Properties Report No. CERN-2013-004 (CERN, 2013); https://doi.org/10.5170/CERN-2013-004
Duhrssen, M. et al. Extracting Higgs boson couplings from CERN LHC data. Phys. Rev. D 70, 113009 (2004).
Dobrescu, B. A. & Lykken, J. D. Coupling spans of the Higgs-like boson. J. High Energy Phys. 2103-02, 73 (2013).
Andersen, J. R. et al. Les Houches 2015: Physics at TeV Colliders Standard Model Working Group Report. In 9th Les Houches Workshop on Physics at TeV Colliders https://inspirehep.net/literature/1459079 (2016).
Berger, N. et al. Simplified Template Cross Sections – Stage 1.1 Report No. LHCHXSWG-2019-003 (CERN, 2019); preprint at https://arxiv.org/abs/1906.02754
Amoroso, S. et al. Les Houches 2019: Physics at TeV Colliders: Standard Model Working Group Report. In 11th Les Houches Workshop on Physics at TeV Colliders: PhysTeV Les Houches https://inspirehep.net/literature/1783782 (2020).
Dainese, A. et al. Report on the Physics at the HL-LHC, and Perspectives for the HE-LHC Report No. CERN-2019-007 (CERN, 2019); https://cds.cern.ch/record/2703572
ATLAS Collaboration. ATLAS Insertable B-Layer: Technical Design Report Report No. CERN-LHCC-2010-013 (CERN, 2010); https://cds.cern.ch/record/1291633
Abbott, B. et al. Production and integration of the ATLAS Insertable B-Layer. J. Instrum. 13, T05008 (2018).
ATLAS Collaboration. Performance of the ATLAS trigger system in 2015. Eur. Phys. J. C 77, 317 (2017).
ATLAS Collaboration. Luminosity Determination in pp Collisions at √s = 13 TeV using the ATLAS Detector at the LHC Report No. ATLAS-CONF-2019-021 (CERN, 2019); https://cds.cern.ch/record/2677054
ATLAS Collaboration. Electron reconstruction and identification in the ATLAS experiment using the 2015 and 2016 LHC proton–proton collision data at √s = 13 TeV. Eur. Phys. J. C 79, 639 (2019).
ATLAS Collaboration. Performance of electron and photon triggers in ATLAS during LHC Run 2. Eur. Phys. J. C 80, 47 (2020).
ATLAS Collaboration. Muon reconstruction and identification efficiency in ATLAS using the full Run 2 pp collision data set at √s = 13 TeV. Eur. Phys. J. C 81, 578 (2021).
ATLAS Collaboration. Measurement of the Tau Lepton Reconstruction and Identification Performance in the ATLAS Experiment using pp Collisions at √s = 13 TeV Report No. ATLAS-CONF-2017-029 (CERN, 2017); https://cds.cern.ch/record/2261772
ATLAS Collaboration. ATLAS b-jet identification performance and efficiency measurement with \(t\bar{t}\) events in pp collisions at √s = 13 TeV. Eur. Phys. J. C 79, 970 (2019).
ATLAS Collaboration. Measurement of the c-jet mistagging efficiency in \(t\bar{t}\) events using pp collision data at √s = 13 TeV collected with the ATLAS detector. Eur. Phys. J. C 82, 95 (2022).
ATLAS Collaboration. Configuration and performance of the ATLAS b-jet triggers in Run 2. Eur. Phys. J. C 81, 1087 (2021).
ATLAS Collaboration. Electron and photon performance measurements with the ATLAS detector using the 2015–2017 LHC proton–proton collision data. J. Instrum. 14, P12006 (2019).
ATLAS Collaboration. Jet energy scale and resolution measured in proton–proton collisions at √s = 13 TeV with the ATLAS detector. Eur. Phys. J. C 81, 689 (2020).
ATLAS Collaboration. Optimisation of large-radius jet reconstruction for the ATLAS detector in 13 TeV proton–proton collisions. Eur. Phys. J. C 81, 334 (2020).
ATLAS Collaboration. Performance of missing transverse momentum reconstruction with the ATLAS detector using proton–proton collisions at √s = 13 TeV. Eur. Phys. J. C 78, 903 (2018).
Butterworth, J. et al. PDF4LHC recommendations for LHC Run II. J. Phys. G 43, 023001 (2016).
ATLAS Collaboration. Evaluation of Theoretical Uncertainties for Simplified Template Cross Section Measurements of V-Associated Production of the Higgs Boson Report No. ATL-PHYS-PUB-2018-035 (CERN, 2018); https://cds.cern.ch/record/2649241
ATLAS Collaboration. Search for the Standard Model Higgs boson in the two photon decay channel with the ATLAS detector at the LHC. Phys. Lett. B 705, 452–470 (2011).
Cacciari, M., Salam, G. P. & Soyez, G. The anti-kt jet clustering algorithm. J. High Energy Phys. 2008-04, 063 (2008).
ATLAS Collaboration. ATLAS Computing Acknowledgements (CERN 2021); https://cds.cern.ch/record/2776662.
Acknowledgements
We thank CERN for the very successful operation of the LHC, as well as the support staff from our institutions without whom ATLAS could not be operated efficiently. We acknowledge the support of ANPCyT, Argentina; YerPhI, Armenia; ARC, Australia; BMWFW and FWF, Austria; ANAS, Azerbaijan; CNPq and FAPESP, Brazil; NSERC, NRC and CFI, Canada; CERN; ANID, Chile; CAS, MOST and NSFC, China; Minciencias, Colombia; MEYS CR, Czech Republic; DNRF and DNSRC, Denmark; IN2P3-CNRS and CEA-DRF/IRFU, France; SRNSFG, Georgia; BMBF, HGF and MPG, Germany; GSRI, Greece; RGC and Hong Kong SAR, China; ISF and Benoziyo Center, Israel; INFN, Italy; MEXT and JSPS, Japan; CNRST, Morocco; NWO, Netherlands; RCN, Norway; MEiN, Poland; FCT, Portugal; MNE/IFA, Romania; MESTD, Serbia; MSSR, Slovakia; ARRS and MIZS, Slovenia; DSI/NRF, South Africa; MICINN, Spain; SRC and Wallenberg Foundation, Sweden; SERI, SNSF and Cantons of Bern and Geneva, Switzerland; MOST, Taiwan; TENMAK, Türkiye; STFC, United Kingdom; DOE and NSF, United States of America. In addition, individual groups and members have received support from BCKDF, CANARIE, Compute Canada and CRC, Canada; PRIMUS 21/SCI/017 and UNCE SCI/013, Czech Republic; COST, ERC, ERDF, Horizon 2020 and Marie Sklodowska-Curie Actions, European Union; Investissements d’Avenir Labex, Investissements d’Avenir Idex and ANR, France; DFG and AvH Foundation, Germany; Herakleitos, Thales and Aristeia programmes co-financed by EUESF and the Greek NSRF, Greece; BSF-NSF and MINERVA, Israel; Norwegian Financial Mechanism 2014-2021, Norway; NCN and NAWA, Poland; La CaixaBanking Foundation, CERCA Programme Generalitat de Catalunya and PROMETEO and GenT Programmes Generalitat Valenciana, Spain; Göran Gustafssons Stiftelse, Sweden; The Royal Society and Leverhulme Trust, United Kingdom. The crucial computing support from all WLCG partners is acknowledged gratefully, in particular from CERN, the ATLAS Tier-1 facilities at TRIUMF (Canada), NDGF (Denmark, Norway, Sweden), CC-IN2P3 (France), KIT/GridKA (Germany), INFN-CNAF (Italy), NL-T1 (Netherlands), PIC (Spain), ASGC (Taiwan), RAL (UK) and BNL (USA), the Tier-2 facilities worldwide and large non-WLCG resource providers. Major contributors of computing resources are listed at ref. 79. The copyright of this Article is held by CERN, for the benefit of the ATLAS Collaboration.
Author information
Authors and Affiliations
Consortia
Contributions
All authors have contributed to the publication, being variously involved in the design and the construction of the detectors, in writing software, calibrating subsystems, operating the detectors and acquiring data, and finally analysing the processed data. The ATLAS Collaboration members discussed and approved the scientific results. The manuscript was prepared by a subgroup of authors appointed by the collaboration and subject to an internal collaboration-wide review process. All authors reviewed and approved the final version of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Matt Kenzie, Zhen Liu and David Sperka for their contribution to the peer review of this work.
Additional information
Extended data
is available for this paper at https://doi.org/10.1038/s41586-022-04893-w.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
The ATLAS Collaboration. A detailed map of Higgs boson interactions by the ATLAS experiment ten years after the discovery. Nature 607, 52–59 (2022). https://doi.org/10.1038/s41586-022-04893-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04893-w
This article is cited by
-
A low-latency graph computer to identify metastable particles at the Large Hadron Collider for real-time analysis of potential dark matter signatures
Scientific Reports (2024)
-
Nanosecond anomaly detection with decision trees and real-time application to exotic Higgs decays
Nature Communications (2024)
-
The precision measurement of the W boson mass and its impact on physics
Nature Reviews Physics (2024)
-
Supersymmetry: a decade after Higgs discovery
Indian Journal of Physics (2023)
-
Limiting FCNC induced by a CP symmetry of order 4
Journal of High Energy Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.