Abstract
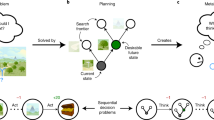
One of the most striking features of human cognition is the ability to plan. Two aspects of human planning stand out—its efficiency and flexibility. Efficiency is especially impressive because plans must often be made in complex environments, and yet people successfully plan solutions to many everyday problems despite having limited cognitive resources1,2,3. Standard accounts in psychology, economics and artificial intelligence have suggested that human planning succeeds because people have a complete representation of a task and then use heuristics to plan future actions in that representation4,5,6,7,8,9,10,11. However, this approach generally assumes that task representations are fixed. Here we propose that task representations can be controlled and that such control provides opportunities to quickly simplify problems and more easily reason about them. We propose a computational account of this simplification process and, in a series of preregistered behavioural experiments, show that it is subject to online cognitive control12,13,14 and that people optimally balance the complexity of a task representation and its utility for planning and acting. These results demonstrate how strategically perceiving and conceiving problems facilitates the effective use of limited cognitive resources.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
Data for the current study are available through the Open Science Foundation repository https://doi.org/10.17605/OSF.IO/ZPQ69.
Code availability
Code for this study is available through the Open Science Foundation repository https://doi.org/10.17605/OSF.IO/ZPQ69, which links to a GitHub repository and contains an archived version of the repository. The value-guided construal model and alternative models were implemented in Python (v.3.7.4) using the msdm (v.0.6) library, numpy (v.1.19.2) and scipy (v.1.5.2). Experiments were implemented using psiTurk (v.3.2.0) and jsPsych (v.6.0.1). Hierarchical generalized linear regressions were implemented using rpy2 (v.3.3.6), lme4 (v.1.1.21) and R (v.3.6.1).
References
Lewis, R. L., Howes, A. & Singh, S. Computational rationality: linking mechanism and behavior through bounded utility maximization. Top. Cogn. Sci. 6, 279–311 (2014).
Griffiths, T. L., Lieder, F. & Goodman, N. D. Rational use of cognitive resources: levels of analysis between the computational and the algorithmic. Top. Cogn. Sci. 7, 217–229 (2015).
Gershman, S. J., Horvitz, E. J. & Tenenbaum, J. B. Computational rationality: a converging paradigm for intelligence in brains, minds, and machines. Science 349, 273–278 (2015).
Newell, A. & Simon, H. A. Human Problem Solving (Prentice Hall, 1972).
Russell, S. & Norvig, P. Artificial Intelligence: A Modern Approach 3rd edn (Prentice Hall, 2009).
Keramati, M., Smittenaar, P., Dolan, R. J. & Dayan, P. Adaptive integration of habits into depth-limited planning defines a habitual-goal–directed spectrum. Proc. Natl Acad. Sci. USA 113, 12868–12873 (2016).
Huys, Q. J. M. et al. Bonsai trees in your head: how the Pavlovian system sculpts goal-directed choices by pruning decision trees. PLoS Comput. Biol. 8, e1002410 (2012).
Huys, Q. J. M. et al. Interplay of approximate planning strategies. Proc. Natl Acad. Sci. USA 112, 3098–3103 (2015).
Callaway, F. et al. Rational use of cognitive resources in human planning. Nat. Hum. Behav. https://doi.org/10.1038/s41562-022-01332-8 (2022).
Sezener, C. E., Dezfouli, A. & Keramati, M. Optimizing the depth and the direction of prospective planning using information values. PLoS Comput. Biol. 15, e1006827 (2019).
Pezzulo, G., Donnarumma, F., Maisto, D. & Stoianov, I. Planning at decision time and in the background during spatial navigation. Curr. Opin. Behav. Sci. 29, 69–76 (2019).
Miller, E. K. & Cohen, J. D. An integrative theory of prefrontal cortex function. Ann. Rev. Neurosci. 24, 167–202 (2001).
Shenhav, A., Botvinick, M. M. & Cohen, J. D. The expected value of control: an integrative theory of anterior cingulate cortex function. Neuron 79, 217–240 (2013).
Shenhav, A. et al. Toward a rational and mechanistic account of mental effort. Ann. Rev. Neurosci. 40, 99–124 (2017).
Norman, D. A. & Shallice, T. in Consciousness and Self-Regulation (eds Davidson, R. J. et al.) 1–18 (Plenum Press, 1986).
Holland, J. H., Holyoak, K. J., Nisbett, R. E. & Thagard, P. R. Induction: Processes of Inference, Learning, and Discovery (MIT Press, 1989).
Newell, A. & Simon, H. A. Computer science as empirical inquiry: symbols and search. Commun. ACM 19, 113–126 (1976).
Daw, N. D., Niv, Y. & Dayan, P. Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 8, 1704–1711 (2005).
Gläscher, J., Daw, N., Dayan, P. & O’Doherty, J. P. States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 66, 585–595 (2010).
Ramkumar, P. et al. Chunking as the result of an efficiency computation trade-off. Nat. Commun. 7, 12176 (2016).
Barsalou, L. W. Ad hoc categories. Mem. Cogn. 11, 211–227 (1983).
Simon, H. A. The functional equivalence of problem solving skills. Cogn. Psychol. 7, 268–288 (1975).
Brooks, R. A. Intelligence without representation. Artif. Intell. 47, 139–159 (1991).
Puterman, M. L. Markov Decision Processes: Discrete Stochastic Dynamic Programming (John Wiley & Sons, 1994).
Bellman, R. Dynamic Programming (Princeton Univ. Press, 1957).
Leong, Y. C., Radulescu, A., Daniel, R., DeWoskin, V. & Niv, Y. Dynamic interaction between reinforcement learning and attention in multidimensional environments. Neuron 93, 451–463 (2017).
Hinton, G. E. Training products of experts by minimizing contrastive divergence. Neural Comput. 14, 1771–1800 (2002).
Whiteley, L. & Sahani, M. Attention in a Bayesian framework. Front. Hum. Neurosci. 6, 100 (2012).
Lieder, F. & Griffiths, T. L. Resource-rational analysis: understanding human cognition as the optimal use of limited computational resources. Behav. Brain Sci. 43, e1 (2020).
Yoo, A. H., Klyszejko, Z., Curtis, C. E. & Ma, W. J. Strategic allocation of working memory resource. Sci. Rep. 8, 16162 (2018).
Grünwald, P. Model selection based on minimum description length. J. Math. Psychol. 44, 133–152 (2000).
Gabaix, X. A sparsity-based model of bounded rationality. Q. J. Econ. 129, 1661–1710 (2014).
Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information (W. H. Freeman, 1982).
Anderson, J. R. The Adaptive Character of Thought (Lawrence Erlbaum Associates, 1990).
Gershman, S. J. The successor representation: its computational logic and neural substrates. J. Neurosci. 38, 7193–7200 (2018).
Stachenfeld, K. L., Botvinick, M. M. & Gershman, S. J. The hippocampus as a predictive map. Nat. Neurosci. 20, 1643–1653 (2017).
Tversky, B. & Hemenway, K. Objects, parts, and categories. J. Exp. Psychol. 113, 169–193 (1984).
Tenenbaum, J. B., Kemp, C., Griffiths, T. L. & Goodman, N. D. How to grow a mind: statistics, structure, and abstraction. Science 331, 1279–1285 (2011).
Nassar, M. R. & Frank, M. J. Taming the beast: extracting generalizable knowledge from computational models of cognition. Curr. Opin. Behav. Sci. 11, 49–54 (2016).
Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction (MIT Press, 2018).
Parr, R. & Russell, S. in Proc. Advances in Neural Information Processing Systems (eds Jordan, M. I. et al.) 10 (MIT Press, 1997).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
Howard, R. A. Dynamic Programming and Markov Processes (MIT Press, 1960).
Barto, A. G., Bradtke, S. J. & Singh, S. P. Learning to act using real-time dynamic programming. Artif. Intell. 72, 81–138 (1995).
Bonet, B. & Geffner, H. Labeled RTDP: improving the convergence of real-time dynamic programming. In Proc. International Conference on Planning and Automated Scheduling Vol. 3 (ed. Giunchiglia, E.) 12–21 (AAAI Press, 2003).
Hansen, E. A. & Zilberstein, S. LAO∗: a heuristic search algorithm that finds solutions with loops. Artif. Intell. 129, 35–62 (2001).
Hart, P. E., Nilsson, N. J. & Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 4, 100–107 (1968).
Momennejad, I. et al. The successor representation in human reinforcement learning. Nat. Hum. Behav. 1, 680–692 (2017).
Harris, C. R. et al. Array programming with NumPy. Nature 585, 357–362 (2020).
Russek, E. M., Momennejad, I., Botvinick, M. M., Gershman, S. J. & Daw, N. D. Predictive representations can link model-based reinforcement learning to model-free mechanisms. PLoS Comput. Biol. 13, e1005768 (2017).
Solway, A. et al. Optimal behavioral hierarchy. PLoS Comput. Biol. 10, e1003779 (2014).
Shi, J. & Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 22, 888–905 (2000).
Gureckis, T. M. et al. psiTurk: an open-source framework for conducting replicable behavioral experiments online. Behav. Res. Methods 48, 829–842 (2016).
De Leeuw, J. R. jsPsych: a JavaScript library for creating behavioral experiments in a web browser. Behav. Res. Methods 47, 1–12 (2015).
Bates, D., Mächler, M., Bolker, B. & Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67, 1–48 (2015).
The rpy2 Contributors. rpy2 version 3.3.6. (2020); https://rpy2.github.io/
Acknowledgements
We thank J. Hamrick, L. Gularte, C. Sayalı, Q. Zhang, R. Dubey and W. Thompson for feedback on this work. This work was funded by NSF grant 1545126, John Templeton Foundation grant 61454 and AFOSR grant FA 9550-18-1-0077.
Author information
Authors and Affiliations
Contributions
All of the authors contributed to conceptualizing the project and editing the manuscript. M.K.H., D.A., M.L.L. and T.L.G. developed the value-guided construal model. M.K.H. implemented the value-guided construal model. M.K.H. and C.G.C. implemented the heuristic search models and msdm library. M.K.H., J.D.C. and T.L.G. designed the experiments. M.K.H. implemented the experiments, analysed the results and drafted the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Wei Ji Ma, Redmond O’Connell and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Experimental measures on mazes 0 to 5.
Average responses associated with each obstacle in mazes 0 to 5 in the initial experiment (awareness judgement), the up-front planning experiment (awareness judgement), and the process-tracing experiment (whether an obstacle was hovered over and, if so, the duration of hovering in log milliseconds). Obstacle colours are normalized by the minimum and maximum values for each measure/maze, except for awareness judgements, which are scaled from 0 to 1.
Extended Data Fig. 2 Experimental measures on mazes 6 to 11.
Average responses associated with each obstacle in mazes 6 to 11 in the initial experiment (awareness judgement), the up-front planning experiment (awareness judgement), and the process-tracing experiment (whether an obstacle was hovered over and, if so, the duration of hovering in log milliseconds). Obstacle colours are normalized by the minimum and maximum values for each measure/maze, except for awareness judgements, which are scaled from 0 to 1.
Extended Data Fig. 3 Experimental measures on mazes 12 to 15.
Average responses associated with each obstacle in mazes 12 to 15 in the critical mazes experiment (recall accuracy, recall confidence, and awareness judgement) and the process-tracing experiment (whether an obstacle was hovered over and, if so, the duration of hovering in log milliseconds). Obstacle colours are scaled to range from 0.5 to 1.0 for accuracy, 0 to 1 for hovering, confidence, and awareness judgements, and the minimum to maximum values across obstacles in a maze for hovering duration in log milliseconds.
Extended Data Fig. 4 Additional Experimental Details.
a, Items from critical mazes experiment. Blue obstacles are the location of obstacles during the navigation part of the trial. Orange obstacles with corresponding number are copies that were shown during location recall probes. During recall probes, participants only saw an obstacle paired with its copy. b, Example trial from process-tracing experiment. Participants could never see all of the obstacles at once, but, before navigating, could use their mouse to reveal obstacles. We analyzed whether value-guided construal predicted which obstacles people tended to hover over and, if so, the duration of hovering.
Extended Data Fig. 5 Model predictions on mazes 0 through 7.
Shown are the predictions for six of the eleven predictors we tested: fixed parameter value-guided construal modification obstacle probability (VGC, our model); trajectory-based heuristic search obstacle hit score (Traj HS); graph-based heuristic search obstacle hit score (Graph HS); distance to optimal bottleneck (Bottleneck); successor representation overlap score (SR Overlap); and distance to optimal paths (Opt Dist) (see Methods, Model Implementations). Mazes 0 to 7 were all in the initial set of mazes. Darker obstacles correspond to greater predicted attention according to the model. Obstacle colours normalized by the minimum and maximum values for each model/maze.
Extended Data Fig. 6 Model predictions on mazes 8 through 15.
Shown are the predictions for six of the eleven predictors we tested (see Methods, Model Implementations). Mazes 8 to 11 were part of the initial set of mazes, while mazes 12 to 15 constituted the set of critical mazes. Darker obstacles correspond to greater predicted attention according to the model. Obstacle colours normalized by the minimum and maximum values for each model/maze.
Extended Data Fig. 7 Summaries of candidate models and data from planning experiments.
Each row corresponds to a measurement of attention to obstacles from a planning experiment: Awareness judgements from the initial memory experiment, the up-front planning experiment, and the critical mazes experiment; recall accuracy and confidence from the critical mazes experiment; and the binary hovering measure and hovering duration measure (in log milliseconds) from the two process-tracing experiments. Each column corresponds to candidate processes that could predict attention to obstacles: fixed parameter value-guided construal modification obstacle probability (VGC, our model), trajectory-based heuristic search hit score (Traj HS), graph-based heuristic search hit score (Graph HS), distance to bottleneck states (Bottleneck), successor-representation overlap (SR Overlap), expected distance to optimal paths (Opt Dist), distance to the goal location (Goal Dist), distance to the start location (Start Dist), distance to the invariant black walls (Wall Dist), and distance to the centre of the maze (Centre Dist). Note that for distance-based predictors, the x-axis is flipped. For each predictor, we quartile-binned the predictions across obstacles, and for each bin we plot (bright red lines) the mean and standard deviation of the predictor and mean by-obstacle response (overlapping bins were collapsed into a single bin). Black circles correspond to the mean response and prediction for each obstacle in each maze. Dashed dark red lines are simple linear regressions on the black circles, with R2 values shown in the lower right of each plot. Across the nine measures, value-guided construal tracks attention to obstacles, while other candidate processes are less consistently associated with obstacle attention (data are based on n = 84215 observations taken from 825 independent participants).
Extended Data Fig. 8 Sufficiency of individual and pairs of mechanisms for explaining attention to obstacles when planning.
To assess the individual and pairwise sufficiency of each predictor for explaining responses in the planning experiments, we fit hierarchical generalized linear models (HGLMs) that included pairs of predictors as fixed effects. Each lower-triangle plot corresponds to one of the experimental measures, where pairs of predictors included in a HGLM as fixed-effects are indicated on the x- and y-axes. Values are the ΔAIC for each model relative to the best fitting model associated with an experimental measure (lower values indicate better fit). Values along the diagonals correspond to models fit with a single predictor. According to this criterion, across all experimental measures, value-guided construal is in the first or second best single-predictor HGLM, and is always in the best two-predictor HGLM.
Supplementary information
Supplementary Information
Supplementary Analyses, Supplementary Discussion, with details of the construal optimization algorithms, Supplementary Methods, Supplementary Tables 1 and 2, Supplementary Figs. 1–12 and Supplementary References.
Rights and permissions
About this article
Cite this article
Ho, M.K., Abel, D., Correa, C.G. et al. People construct simplified mental representations to plan. Nature 606, 129–136 (2022). https://doi.org/10.1038/s41586-022-04743-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04743-9
This article is cited by
-
Using deep neural networks as a guide for modeling human planning
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.