Abstract
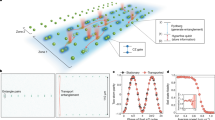
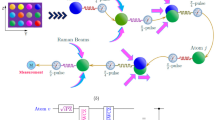
Interactions govern the flow of information and the formation of correlations between constituents of many-body quantum systems, dictating phases of matter found in nature and forms of entanglement generated in the laboratory. Typical interactions decay with distance and thus produce a network of connectivity governed by geometry—such as the crystalline structure of a material or the trapping sites of atoms in a quantum simulator1,2. However, many envisioned applications in quantum simulation and computation require more complex coupling graphs including non-local interactions, which feature in models of information scrambling in black holes3,4,5,6 and mappings of hard optimization problems onto frustrated classical magnets7,8,9,10,11. Here we describe the realization of programmable non-local interactions in an array of atomic ensembles within an optical cavity, in which photons carry information between atomic spins12,13,14,15,16,17,18,19. By programming the distance dependence of the interactions, we access effective geometries for which the dimensionality, topology and metric are entirely distinct from the physical geometry of the array. As examples, we engineer an antiferromagnetic triangular ladder, a Möbius strip with sign-changing interactions and a treelike geometry inspired by concepts of quantum gravity5,20,21,22. The tree graph constitutes a toy model of holographic duality21,22, in which the quantum system lies on the boundary of a higher-dimensional geometry that emerges from measured correlations23. Our work provides broader prospects for simulating frustrated magnets and topological phases24, investigating quantum optimization paradigms10,11,25,26 and engineering entangled resource states for sensing and computation27,28.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Code availability
All code used for simulation and analysis is available from the corresponding author upon reasonable request.
Change history
11 March 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41586-022-04610-7
References
Bloch, I., Dalibard, J. & Nascimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 8, 267–276 (2012).
Browaeys, A. & Lahaye, T. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 16, 132–142 (2020).
Hayden, P. & Preskill, J. Black holes as mirrors: quantum information in random subsystems. J. High Energy Phys. 2007, 120–120 (2007).
Maldacena, J. & Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D 94, 106002 (2016).
Bentsen, G. et al. Treelike interactions and fast scrambling with cold atoms. Phys. Rev. Lett. 123, 130601 (2019).
Belyansky, R., Bienias, P., Kharkov, Y. A., Gorshkov, A. V. & Swingle, B. Minimal model for fast scrambling. Phys. Rev. Lett. 125, 130601 (2020).
Das, A. & Chakrabarti, B. K. Colloquium: quantum annealing and analog quantum computation. Rev. Mod. Phys. 80, 1061–1081 (2008).
Gopalakrishnan, S., Lev, B. L. & Goldbart, P. M. Frustration and glassiness in spin models with cavity-mediated interactions. Phys. Rev. Lett. 107, 277201 (2011).
Strack, P. & Sachdev, S. Dicke quantum spin glass of atoms and photons. Phys. Rev. Lett. 107, 277202 (2011).
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617 (2016).
Berloff, N. G. et al. Realizing the classical XY Hamiltonian in polariton simulators. Nat. Mater. 16, 1120–1126 (2017).
Leroux, I. D., Schleier-Smith, M. H. & Vuletić, V. Implementation of cavity squeezing of a collective atomic spin. Phys. Rev. Lett. 104, 073602 (2010).
Barontini, G., Hohmann, L., Haas, F., Estève, J. & Reichel, J. Deterministic generation of multiparticle entanglement by quantum Zeno dynamics. Science 349, 1317–1321 (2015).
Hosten, O., Krishnakumar, R., Engelsen, N. J. & Kasevich, M. A. Quantum phase magnification. Science 352, 1552–1555 (2016).
Pedrozo-Peñafiel, E. et al. Entanglement on an optical atomic-clock transition. Nature 588, 414–418 (2020).
Welte, S., Hacker, B., Daiss, S., Ritter, S. & Rempe, G. Photon-mediated quantum gate between two neutral atoms in an optical cavity. Phys. Rev. X 8, 011018 (2018).
Davis, E. J., Bentsen, G., Homeier, L., Li, T. & Schleier-Smith, M. H. Photon-mediated spin-exchange dynamics of spin-1 atoms. Phys. Rev. Lett. 122, 010405 (2019).
Davis, E. J. et al. Protecting spin coherence in a tunable Heisenberg model. Phys. Rev. Lett. 125, 060402 (2020).
Muniz, J. A. et al. Exploring dynamical phase transitions with cold atoms in an optical cavity. Nature 580, 602–607 (2020).
Barbón, J. L. & Magán, J. M. Fast scramblers and ultrametric black hole horizons. J. High Energy Phys. 2013, 163 (2013).
Gubser, S. S., Knaute, J., Parikh, S., Samberg, A. & Witaszczyk, P. p-adic AdS/CFT. Commun. Math. Phys. 352, 1019–1059 (2017).
Heydeman, M., Marcolli, M., Saberi, I. & Stoica, B. Tensor networks, p-adic fields, and algebraic curves: arithmetic and the AdS3/CFT2 correspondence. Preprint at https://arxiv.org/abs/1605.07639 (2016).
Qi, X.-L. Does gravity come from quantum information? Nat. Phys. 14, 984–987 (2018).
Hung, C.-L., González-Tudela, A., Cirac, J. I. & Kimble, H. J. Quantum spin dynamics with pairwise-tunable, long-range interactions. Proc. Natl Acad. Sci. USA 113, E4946–E4955 (2016).
Marsh, B. P. et al. Enhancing associative memory recall and storage capacity using confocal cavity QED. Phys. Rev. X 11, 021048 (2021).
Anikeeva, G. et al. Number partitioning with Grover’s algorithm in central spin systems. PRX Quantum 2, 020319 (2021).
Masson, S. J., Barrett, M. & Parkins, S. Cavity QED engineering of spin dynamics and squeezing in a spinor gas. Phys. Rev. Lett. 119, 213601 (2017).
Qin, Z. et al. Characterizing the multipartite continuous-variable entanglement structure from squeezing coefficients and the Fisher information. npj Quantum Inf. 5, 3 (2019).
Pezzè, L., Smerzi, A., Oberthaler, M. K., Schmied, R. & Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 90, 035005 (2018).
Omran, A. et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 365, 570–574 (2019).
Hamley, C. D., Gerving, C., Hoang, T., Bookjans, E. & Chapman, M. S. Spin-nematic squeezed vacuum in a quantum gas. Nat. Phys. 8, 305–308 (2012).
Fadel, M., Zibold, T., Décamps, B. & Treutlein, P. Spatial entanglement patterns and Einstein-Podolsky-Rosen steering in Bose-Einstein condensates. Science 360, 409–413 (2018).
Kunkel, P. et al. Spatially distributed multipartite entanglement enables EPR steering of atomic clouds. Science 360, 413–416 (2018).
Lange, K. et al. Entanglement between two spatially separated atomic modes. Science 360, 416–418 (2018).
Islam, R. et al. Emergence and frustration of magnetism with variable-range interactions in a quantum simulator. Science 340, 583–587 (2013).
Jurcevic, P. et al. Quasiparticle engineering and entanglement propagation in a quantum many-body system. Nature 511, 202–205 (2014).
Vaidya, V. D. et al. Tunable-range, photon-mediated atomic interactions in multimode cavity QED. Phys. Rev. X 8, 011002 (2018).
Manovitz, T., Shapira, Y., Akerman, N., Stern, A. & Ozeri, R. Quantum simulations with complex geometries and synthetic gauge fields in a trapped ion chain. PRX Quantum 1, 020303 (2020).
Kollár, A. J., Fitzpatrick, M. & Houck, A. A. Hyperbolic lattices in circuit quantum electrodynamics. Nature 571, 45–50 (2019).
Lücke, B. et al. Detecting multiparticle entanglement of Dicke states. Phys. Rev. Lett. 112, 155304 (2014).
Lee, S. & Lee, K.-C. Phase transitions in the fully frustrated triangular XY model. Phys. Rev. B 57, 8472 (1998).
Gubser, S. S., Jepsen, C., Ji, Z. & Trundy, B. Continuum limits of sparse coupling patterns. Phys. Rev. D 98, 045009 (2018).
Shi, Y.-Y., Duan, L.-M. & Vidal, G. Classical simulation of quantum many-body systems with a tree tensor network. Phys. Rev. A 74, 022320 (2006).
Murg, V., Verstraete, F., Legeza, Ö. & Noack, R. M. Simulating strongly correlated quantum systems with tree tensor networks. Phys. Rev. B 82, 205105 (2010).
Pastawski, F., Yoshida, B., Harlow, D. & Preskill, J. Holographic quantum error-correcting codes: toy models for the bulk/boundary correspondence. J. High Energ. Phys. 2015, 149 (2015).
Amit, D. J., Gutfreund, H. & Sompolinsky, H. Spin-glass models of neural networks. Phys. Rev. A 32, 1007–1018 (1985).
Aidelsburger, M. et al. Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nat. Phys. 11, 162–166 (2015).
Kennedy, C. J., Burton, W. C., Chung, W. C. & Ketterle, W. Observation of Bose–Einstein condensation in a strong synthetic magnetic field. Nat. Phys. 11, 859–864 (2015).
Zeiher, J. et al. Microscopic characterization of scalable coherent Rydberg superatoms. Phys. Rev. X 5, 031015 (2015).
Evans, R. E. et al. Photon-mediated interactions between quantum emitters in a diamond nanocavity. Science 362, 662–665 (2018).
Lee, J., Vrijsen, G., Teper, I., Hosten, O. & Kasevich, M. A. Many-atom–cavity QED system with homogeneous atom–cavity coupling. Opt. Lett. 39, 4005–4008 (2014).
Xu, V. et al. Probing gravity by holding atoms for 20 seconds. Science 366, 745–749 (2019).
Sørensen, A. S. & Mølmer, K. Entangling atoms in bad cavities. Phys. Rev. A 66, 022314 (2002).
Stamper-Kurn, D. M. & Ueda, M. Spinor Bose gases: symmetries, magnetism, and quantum dynamics. Rev. Mod. Phys. 85, 1191 (2013).
Sinatra, A., Lobo, C. & Castin, Y. The truncated Wigner method for Bose-condensed gases: limits of validity and applications. J. Phys. B 35, 3599–3631 (2002).
Blakie, P. B., Bradley, A. S., Davis, M. J., Ballagh, R. J. & Gardiner, C. W. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques. Adv. Phys. 57, 363–455 (2008).
Lewis-Swan, R. J., Olsen, M. K. & Kheruntsyan, K. V. Approximate particle number distribution from direct stochastic sampling of the Wigner function. Phys. Rev. A 94, 033814 (2016).
Lauritzen, S. L. Graphical Models Vol. 17 (Clarendon Press, 1996).
Acknowledgements
We thank S. Gubser for discussions that inspired our exploration of non-Archimedean geometry. We also acknowledge discussions with G. Bentsen, A. Daley, I. Bloch, B. Lev, N. Berloff, A. Deshpande, B. Swingle and P. Hayden. This work was supported by the DOE Office of Science, Office of High Energy Physics and Office of Basic Energy Sciences under grant no. DE-SC0019174. A.P. and E.S.C. acknowledge support from the NSF under grant no. PHY-1753021. We additionally acknowledge support from the National Defense Science and Engineering Graduate Fellowship (A.P.), the NSF Graduate Research Fellowship Program (E.J.D. and E.S.C.), the Hertz Foundation (E.J.D.) and the German Academic Scholarship Foundation (J.F.W.).
Author information
Authors and Affiliations
Contributions
A.P., E.S.C., P.K., J.F.W. and E.J.D. performed the experiments. A.P., E.S.C., P.K. and M.S.-S. analysed the experimental data and developed supporting theoretical models. A.P., E.S.C., P.K. and M.S.-S. wrote the manuscript. All authors contributed to the discussion and interpretation of results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Robert Lewis-Swan and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Coupling graphs.
Sketch of couplings \(J(i-j)\) for the model in equation (4) with local interactions (s = − 1, left) or treelike interactions (s = 1, right). The strengths of the interactions are indicated by the thickness and transparency of the red lines. For s = 1, reordering the sites according to the Monna map makes the couplings more local, corroborating the treelike geometry.
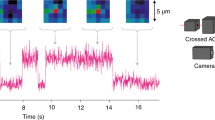
Extended Data Fig. 2 Experimental sequence and imaging.
a Schematic of experimental sequence for measurements of \({F}_{i}^{x}\). After driving the cavity to induce interactions, we apply spin rotations sequentially to the M sites of the array and subsequently perform state-sensitive readout via fluorescence imaging. b Fluorescence images after spin rotation, showing the signal for the F = 2 manifold and the three magnetic substates for the case of interactions at distance r = 3 with periodic boundary conditions. c Transverse magnetization \({F}_{i}^{x}\) and structure factor \({\tilde{F}}_{k}^{x}\) extracted from the image in b.
Extended Data Fig. 3 Effect of finite statistics.
Left, correlation plot reproduced from Fig. 1, showing \({C}^{{\rm{pm}}}\) obtained from 50 realizations of the experiment with interactions at distance r = 10. Right, simulation results obtained from a truncated Wigner approximation, where we either choose the same number of realisations as in the experiment or increase the number of realisations by a factor of 10 to reduce statistical uncertainty. The simulations indicate that residual correlations in the experimental data are mainly due to the finite sample size.
Extended Data Fig. 4 Comparison between measured structure factor and simulation results.
The left graph shows the measured structure factor after T = 3 Bloch periods of evolution, which is also shown in Fig. 2c. The two plots at right show results of a truncated Wigner simulation with and without periodic boundary conditions. For the simulated data we used 100 realizations of the TWA simulation, which is four times higher than the number of experimental realizations to reduce statistical fluctuations. For open boundary conditions, we find that the simulation has an offset with respect to the theoretical prediction (blue line). We attribute this offset to the finite system size, as the model is exact only for an infinite system or a system with periodic boundary conditions. Repeating the same simulation with a pulsed drive shown on the right shows that in this case the TWA simulation is consistent with the analytical model. The error bars indicate the standard error of the mean.
Supplementary information
Rights and permissions
About this article
Cite this article
Periwal, A., Cooper, E.S., Kunkel, P. et al. Programmable interactions and emergent geometry in an array of atom clouds. Nature 600, 630–635 (2021). https://doi.org/10.1038/s41586-021-04156-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-04156-0
This article is cited by
-
Graph states of atomic ensembles engineered by photon-mediated entanglement
Nature Physics (2024)
-
Cavity-mediated long-range interactions in levitated optomechanics
Nature Physics (2024)
-
Many-body cavity quantum electrodynamics with driven inhomogeneous emitters
Nature (2023)
-
Engineering random spin models with atoms in a high-finesse cavity
Nature Physics (2023)
-
High-fidelity parallel entangling gates on a neutral-atom quantum computer
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.