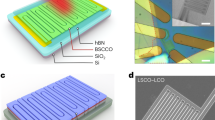
Abstract
Quantum emitters respond to resonant illumination by radiating part of the absorbed energy. A component of this radiation field is phase coherent with the driving tone, whereas another component is incoherent and consists of spontaneously emitted photons, forming the fluorescence signal1. Atoms, molecules and colour centres are routinely detected by their fluorescence at optical frequencies, with important applications in quantum technology2,3 and microscopy4,5,6,7. By contrast, electron spins are usually detected by the phase-coherent echoes that they emit in response to microwave driving pulses8. The incoherent part of their radiation—a stream of microwave photons spontaneously emitted upon individual spin relaxation events—has not been observed so far because of the low spin radiative decay rate and of the lack of single microwave photon detectors (SMPDs). Here using superconducting quantum devices, we demonstrate the detection of a small ensemble of donor spins in silicon by their fluorescence at microwave frequencies and millikelvin temperatures. We enhance their radiative decay rate by coupling them to a high-quality-factor and small-mode-volume superconducting resonator9, and we connect the device output to a newly developed SMPD10 based on a superconducting qubit. In addition, we show that the SMPD can be used to detect spin echoes and that standard spin characterization measurements (Rabi nutation and spectroscopy) can be achieved with both echo and fluorescence detection. We discuss the potential of SMPD detection as a method for magnetic resonance spectroscopy of small numbers of spins.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets acquired and analysed during the current study are available from the corresponding author on reasonable request.
References
Mandel, L. & Wolf, E. Optical Coherence and Quantum Optics (Cambridge Univ. Press, 1995).
Kimble, H. J., Dagenais, M. & Mandel, L. Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 39, 691–695 (1977).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Orrit, M. & Bernard, J. Single pentacene molecules detected by fluorescence excitation in a p-terphenyl crystal. Phys. Rev. Lett. 65, 2716–2719 (1990).
Klar, T. A., Jakobs, S., Dyba, M., Egner, A. & Hell, S. W. Fluorescence microscopy with diffraction resolution barrier broken by stimulated emission. Proc. Natl Acad. Sci. USA 97, 8206–8210 (2000).
Betzig, E. et al. Imaging intracellular fluorescent proteins at nanometer resolution. Science 313, 1642–1645 (2006).
Bruschini, C., Homulle, H., Antolovic, I. M., Burri, S. & Charbon, E. Single-photon avalanche diode imagers in biopho tonics: review and outlook. Light Sci. Appl. 8, 87 (2019).
Schweiger, A. & Jeschke, G. Principles of Pulse Electron Paramagnetic Resonance (Oxford Univ. Press, 2001).
Bienfait, A. et al. Controlling spin relaxation with a cavity. Nature 531, 74–77 (2016).
Lescanne, R. et al. Irreversible qubit-photon coupling for the detection of itinerant microwave photons. Phys. Rev. 10, 021038 (2020).
Roy, A. & Devoret, M. Introduction to parametric amplification of quantum signals with Josephson circuits. C. R. Phys. 17, 740–755 (2016).
Bienfait, A. et al. Reaching the quantum limit of sensitivity in electron spin resonance. Nat. Nanotechnol. 11, 253–257 (2016).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 62320 (2004).
Lamoreaux, S. K., van Bibber, K. A., Lehnert, K. W. & Carosi, G. Analysis of single-photon and linear amplifier detectors for microwave cavity dark matter axion searches. Phys. Rev. D 88, 035020 (2013).
Gleyzes, S. et al. Quantum jumps of light recording the birth and death of a photon in a cavity. Nature 446, 297–300 (2007).
Chen, Y.-F. et al. Microwave photon counter based on Josephson junctions. Phys. Rev. Lett. 107, 217401 (2011).
Inomata, K. et al. Single microwave-photon detector using an artificial lambda-type three-level system. Nat. Commun. 7, 12303 (2016).
Narla, A. et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. 6, 031036 (2016).
Besse, J.-C. et al. Single-shot quantum nondemolition detection of individual itinerant microwave photons. Phys. Rev. 8, 021003 (2018).
Kono, S., Koshino, K., Tabuchi, Y., Noguchi, A. & Nakamura, Y. Quantum non-demolition detection of an itinerant microwave photon. Nat. Phys. 14, 546–549 (2018).
Astner, T. et al. Solid-state electron spin lifetime limited by phononic vacuum modes. Nat. Mater. 17, 313–317 (2018).
Eichler, C., Sigillito, A. J., Lyon, S. A. & Petta, J. R. Electron spin resonance at the level of 104 spins using low impedance superconducting resonators. Phys. Rev. Lett. 118, 037701 (2017).
Sleator, T., Hahn, E. L., Hilbert, C. & Clarke, J. Nuclear-spin noise. Phys. Rev. Lett. 55, 1742 (1985).
McCoy, M. A. & Ernst, R. R. Nuclear spin noise at room temperature. Chem. Phys. Lett. 159, 587–593 (1989).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143–147 (2012).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Palacios-Laloy, A. et al. Tunable resonators for quantum circuits. J. Low Temp. Phys. 151, 1034–1042 (2008).
Gao, J. et al. Exper imental evidence for a surface distribution of two-level systems in superconducting lithographed microwave resonators. Appl. Phys. Lett. 92, 152505 (2008).
Zhu, X. et al. Coherent coupling of a superconducting flux qubit to an electron spin ensemble in diamond. Nature 478, 221–224 (2011).
Kubo, Y. et al. Electron spin resonance detected by a super conducting qubit. Phys. Rev. B 86, 064514 (2012).
Toida, H. et al. Electron paramagnetic resonance spectroscopy using a single artificial atom. Commun. Phys. 2, 33 (2019).
Budoyo, R., Kakuyanagi, K., Toida, H., Matsuzaki, Y. & Saito, S. Electron spin resonance with up to 20 spin sensitivity measured using a superconducting flux qubit. Appl. Phys. Lett. 116, 194001 (2020).
Ranjan, V. et al. Electron spin resonance spectroscopy with femtoliter detection volume. Appl. Phys. Lett. 116, 184002 (2020).
Abella, I. D., Kurnit, N. A. & Hartmann, S. R. Photon echoes. Phys. Rev. 141, 391–406 (1966).
Ranjan, V. et al. Pulsed electron spin resonance spectroscopy in the Purcell regime. J. Magn. Reson. 310, 106662 (2020).
Royer, B., Grimsmo, A. L., Choquette-Poitevin, A. & Blais, A. Itinerant microwave photon detector. Phys. Rev. Lett. 120, 203602 (2018).
Grimsmo, A. L. et al. Quantum metamaterial for broadband detection of single microwave photons. Phys. Rev. Appl. 15, 034074 (2021).
Kokkoniemi, R. et al. Bolometer operating at the threshold for circuit quantum electrodynamics. Nature 586, 47–51 (2020).
Zhou, X. et al. High-gain weakly nonlinear flux-modulated Josephson parametric amplifier using a SQUID array. Phys. Rev. B 89, 214517 (2014).
Dunsworth, A. et al. Characterization and reduction of capacitive loss induced by sub-micron Josephson junction fabrication in superconducting qubits. Appl. Phys. Lett. 111, 022601 (2017).
Bruno, A. et al. Reducing intrinsic loss in superconducting resonators by surface treatment and deep etching of silicon substrates. Appl. Phys. Lett. 106, 182601 (2015).
Calusine, G. et al. Analysis and mitigation of interface losses in trenched superconducting coplanar waveguide resonators. Appl. Phys. Lett. 112, 062601 (2018).
Pla, J. et al. Strain-induced spin-resonance shifts in silicon devices. Phys. Rev. Appl. 9, 044014 (2018).
Gambetta, J. et al. Qubit-photon interactions in a cavity: measurement-induced dephasing and number splitting. Phys. Rev. A 74, 042318 (2006).
Probst, S. et al. Inductive-detection electron-spin resonance spectroscopy with 65 spins/√Hz sensitivity. Appl. Phys. Lett. 111, 202604 (2017).
Acknowledgements
We acknowledge technical support from P. Sénat, D. Duet, P.-F. Orfila and S. Delprat, and are grateful for discussions within the Quantronics group. This project has received funding from the European Union Horizon 2020 research and innovation programme under Marie Sklodowska-Curie grant agreement number 765267 (QuSCO). E.F. has received funding from the Agence Nationale de la Recherche (ANR) under grant agreement number DARKWADOR:ANR-19-CE47-0004. We acknowledge support from the Agence Nationale de la Recherche (ANR) through the Chaire Industrielle NASNIQ under contract ANR-17-CHIN-0001 cofunded by Atos, and of the Région Ile-de-France through the DIM SIRTEQ (REIMIC project).
Author information
Authors and Affiliations
Contributions
E.A., P.B. and E.F. designed the experiment. T.S. provided the bismuth-implanted isotopically purified silicon sample, on which V.R. fabricated the aluminium resonator. E.A. designed and fabricated the SMPD with the help of D.V. and E.F. E.A., V.R. and E.F. performed the measurements, with help from L.B., D.F. and P.B. E.A., P.B. and E.F. analysed the data. E.A., E.B. and V.R. performed the simulations. E.A., P.B. and E.F. wrote the manuscript. D.F., D.V. and D.E. contributed useful input to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Gunnar Jeschke and Stefan Putz for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Schematic of the setup.
Wiring diagram at room temperature and cryogenic temperature extensively described in the methods.
Extended Data Fig. 2 ESR spectroscopy of the spin ensemble.
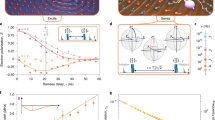
a, Measured (blue dots) and simulated (solid line) integrated echo as a function of the delay τ between the inversion π pulse and the Hahn echo sequence. An exponential fit (not shown) yield a characteristic decay time \({T}_{1}=300\pm 10\,{\rm{ms}}\). b, Measured (blue dots) and simulated (solid line) integrated echo as a function of the delay τ between π/2 and π pulses of the Hahn echo sequence. An exponential fit (not showed) yields a characteristic decay time T2 = 2.7 ms. c, Measured (blue dots) and simulated (solid line) integrated echo as a function of the amplitude A of the π pulse of the Hahn echo sequence revealing Rabi oscillations. d, Measured integrated echo (blue dots) as a function of the in-plane magnetic field B0 used to tune the spin ensemble frequency.
Extended Data Fig. 3 SMPD characterization.
a, Measured (blue dots) and fitted (orange solid line) complex reflection coefficient r of the buffer resonator at working point \({\omega }_{{\rm{b}}}/2{\rm{\pi }}=6.946\,{\rm{G}}{\rm{H}}{\rm{z}}\). The fitting function takes into account flux noise of the SQUID enabling the tuning of the resonator. b, d, Probability \({P}_{{\rm{e}}}\) of finding the qubit in its excited state (color scale) as function of the amplitude \({A}_{{\rm{pump}}}\) and frequency \({\omega }_{{\rm{pump}}}/2{\rm{\pi }}\) of the pump activating the parametric process of photo-detection. When no photon is impinging, the buffer resonator is close to its vacuum state (b) no parametric process is activated and the qubit is mostly in its ground state \({P}_{{\rm{e}}}\approx 0\); in contrast, when photons are injected (d) the parametric process is activated at pump frequencies for which the conservation of energy is respected. The quadratic dependence of the pump activation frequency on the pump amplitude is due to the Stark shift of the qubit frequency for increasing pump power. c, Measured (blue dots) efficiency of detection \({\eta }_{{\rm{d}}}\) at \({\omega }_{{\rm{b}}}=6.946{\rm{G}}{\rm{H}}{\rm{z}}\), as a function of the input photon frequency \({\omega }_{{\rm{photon}}}/2{\rm{\pi }}\). From the fit (orange solid line), obtained with a model of two coupled cavities, we extract a bandwidth \({\Delta }_{det}/2{\rm{\pi }}\approx 2.1{\rm{M}}{\rm{H}}{\rm{z}}\).
Extended Data Fig. 4 SMPD performance.
a, b, Probability \(p(V)\) of measuring the average quadrature voltage V when probing the buffer resonator for qubit readout, when a pulse is applied (b) or not (a) to the qubit prior to the measurement. Dashed line indicates the readout threshold, chosen to minimise the ratio \({\nu }_{{\rm{dc}}}/{\eta }_{{\rm{d}}}\), each measure falling on the left (resp. right) is associated to the qubit being in its ground (resp. excited) state. c, Measured (blue dots) and fitted (orange solid line) probability \({p}_{{\rm{e}}}\) of finding the qubit in its excited state as function of time T after the reset sequence, showing out-of-equilibrium qubit excited population reaching thermal equilibrium on a timescale \(\approx {T}_{1}\). Black dashed line at \({t}_{{\rm{D}}}=5\,{\rm{\mu }}{\rm{s}}\) marks the point at which detector is operated. d, Measured (blue dots) and fitted (orange solid line) detector efficiency \({\eta }_{{\rm{d}}}\) as a function of the duration of the detection step \({t}_{{\rm{D}}}\). Fit model takes into account bandwidth-limited detection efficiency for short detection windows and T1-decay effect for increasing \({t}_{{\rm{d}}}\). Black dashed line at \({t}_{{\rm{D}}}=5\,{\rm{\mu }}{\rm{s}}\) marks the point at which detector is operated, to optimise the photo-detected echo signal. e, Dark count rate \({\nu }_{{\rm{dc}}}\) as a function of time when a train of photo-detection sequences is continuously sent to the fridge. An equilibrium value \(\approx 1.5{{\rm{m}}{\rm{s}}}^{-1}\) is reached and maintained during all the measurements.
Extended Data Fig. 5 Spin ensemble simulations.
a, Measured (blue dots) and simulated (orange solid line) electromagnetic field amplitude at the output of the spin cavity as a function of the time T from the π/2 pulse of an echo sequence. The echo appears as a slight increase of the field amplitude at twice the separation between the π/2 and π pulse (inset). The spin spectral density \({\rho }_{{\rm{spin}}}\) is the only free parameter of the simulation, accordance with the experimental data is achieved for \({\rho }_{{\rm{s}}{\rm{p}}{\rm{i}}{\rm{n}}}=14.6{{\rm{s}}{\rm{p}}{\rm{i}}{\rm{n}}{\rm{s}}{\rm{k}}{\rm{H}}{\rm{z}}}^{-1}\). b, Simulated time evolution of \(\langle {S}_{{\rm{z}}}\rangle \) during an echo sequence, using the same pulse parameters as in the experiment. c, Simulation of the time evolution of \(\langle {S}_{{\rm{z}}}\rangle \) during a π-pulse with the same parameters of the experiment of photo-detected incoherent relaxation. A spin density \({\rho }_{{\rm{s}}{\rm{p}}{\rm{i}}{\rm{n}}}=12{{\rm{s}}{\rm{p}}{\rm{i}}{\rm{n}}{\rm{s}}{\rm{k}}{\rm{H}}{\rm{z}}}^{-1}\) was adjusted so that the ratio between the variation of \(\langle {S}_{z}\rangle \) at echo time (b) and upon the π pulse excitation (c) reproduces the experimental ratio \({C}_{{\rm{spin}}}/({\eta }_{{\rm{duty}}}{c}_{{\rm{e}}})\).
Supplementary information
Rights and permissions
About this article
Cite this article
Albertinale, E., Balembois, L., Billaud, E. et al. Detecting spins by their fluorescence with a microwave photon counter. Nature 600, 434–438 (2021). https://doi.org/10.1038/s41586-021-04076-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-04076-z
This article is cited by
-
Observation of Josephson harmonics in tunnel junctions
Nature Physics (2024)
-
Single-electron spin resonance detection by microwave photon counting
Nature (2023)
-
Magnetometry of neurons using a superconducting qubit
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.