Abstract
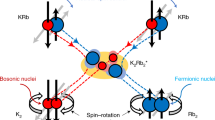
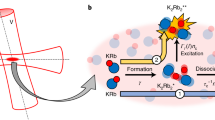
Chemical reactions represent a class of quantum problems that challenge both the current theoretical understanding and computational capabilities1. Reactions that occur at ultralow temperatures provide an ideal testing ground for quantum chemistry and scattering theories, because they can be experimentally studied with unprecedented control2, yet display dynamics that are highly complex3. Here we report the full product state distribution for the reaction 2KRb → K2 + Rb2. Ultracold preparation of the reactants allows us complete control over their initial quantum degrees of freedom, whereas state-resolved, coincident detection of both products enables the probability of scattering into each of the 57 allowed rotational state-pairs to be measured. Our results show an overall agreement with a state-counting model based on statistical theory4,5,6, but also reveal several deviating state-pairs. In particular, we observe a strong suppression of population in the state-pair closest to the exoergicity limit as a result of the long-range potential inhibiting the escape of products. The completeness of our measurements provides a benchmark for quantum dynamics calculations beyond the current state of the art.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The computer codes used for theoretical calculations in this study are available from H.G. (hguo@unm.edu) upon reasonable request.
References
Li, J., Zhao, B., Xie, D. & Guo, H. Advances and new challenges to bimolecular reaction dynamics theory. J. Phys. Chem. Lett. 11, 8844–8860 (2020).
Quéméner, G. & Julienne, P. S. Ultracold molecules under control! Chem. Rev. 112, 4949–5011 (2012).
Croft, J. et al. Universality and chaoticity in ultracold K + KRb chemical reactions. Nat. Commun. 8, 15897 (2017).
Light, J. C. Statistical theory of bimolecular exchange reactions. Discuss. Faraday Soc. 44, 14–29 (1967).
Nikitin, E. E. & Umanskii, S. Y. Theory of Slow Atomic Collisions Vol. 30 (Springer Science & Business Media, 2012).
Pechukas, P. in Dynamics of Molecular Collisions 269–322 (Springer, 1976).
Julienne, P. S. Ultracold molecules from ultracold atoms: a case study with the KRb molecule. Faraday Discuss. 142, 361–388 (2009).
Balakrishnan, N. Ultracold molecules and the dawn of cold controlled chemistry. J. Chem. Phys. 145, 150901 (2016).
Tarbutt, M. R. Laser cooling of molecules. Contemp. Phys. 59, 356–376 (2018).
Toscano, J., Lewandowski, H. & Heazlewood, B. R. Cold and controlled chemical reaction dynamics. Phys. Chem. Chem. Phys. 22, 9180–9194 (2020).
Ospelkaus, S. et al. Quantum-state controlled chemical reactions of ultracold potassium-rubidium molecules. Science 327, 853–857 (2010).
Ni, K.-K. et al. Dipolar collisions of polar molecules in the quantum regime. Nature 464, 1324 (2010).
Guo, M. et al. Dipolar collisions of ultracold ground-state bosonic molecules. Phys. Rev. X 8, 041044 (2018).
Yang, H. et al. Observation of magnetically tunable Feshbach resonances in ultracold 23Na40K + 40K collisions. Science 363, 261–264 (2019).
de Jongh, T. et al. Imaging the onset of the resonance regime in low-energy NO-He collisions. Science 368, 626–630 (2020).
Rui, J. et al. Controlled state-to-state atom-exchange reaction in an ultracold atom–dimer mixture. Nat. Phys. 13, 699 (2017).
Wolf, J. et al. State-to-state chemistry for three-body recombination in an ultracold rubidium gas. Science 358, 921–924 (2017).
Yang, X. State-to-state dynamics of elementary bimolecular reactions. Annu. Rev. Phys. Chem. 58, 433–459 (2007).
Clary, D. C. Theoretical studies on bimolecular reaction dynamics. Proc. Natl Acad. Sci. USA 105, 12649–12653 (2008).
Croft, J. F. & Bohn, J. L. Long-lived complexes and chaos in ultracold molecular collisions. Phys. Rev. A 89, 012714 (2014).
Liu, Y. et al. Photo-excitation of long-lived transient intermediates in ultracold reactions. Nat. Phys. 16, 1132–1136 (2020).
Gregory, P. D., Blackmore, J. A., Bromley, S. L. & Cornish, S. L. Loss of ultracold 87Rb123Cs molecules via optical excitation of long-lived two-body collision complexes. Phys. Rev. Lett. 124, 163402 (2020).
Bonnet, L. & Rayez, J. C. Some key factors of energy distributions in the products of complex-forming elementary reactions. Phys. Chem. Chem. Phys. 1, 2383–2400 (1999).
Balucani, N. et al. Experimental and theoretical differential cross sections for the N(2D)+ H2 reaction. J. Phys. Chem. A 110, 817–829 (2006).
Sun, Z. et al. State-to-state dynamics of H + O2 reaction, evidence for nonstatistical behavior. J. Am. Chem. Soc. 130, 14962–14963 (2008).
Rivero-Santamaría, A. et al. The O(1D)+ H2 (X1Σ+, v, j) → OH (X2∏, v′, j′)+ H(2S) reaction at low collision energy: when a simple statistical description of the dynamics works. Phys. Chem. Chem. Phys. 13, 8136–8139 (2011).
González-Martínez, M. L., Dulieu, O., Larrégaray, P. & Bonnet, L. Statistical product distributions for ultracold reactions in external fields. Phys. Rev. A 90, 052716 (2014).
Nesbitt, D. J. Toward state-to-state dynamics in ultracold collisions: lessons from high-resolution spectroscopy of weakly bound molecular complexes. Chem. Rev. 112, 5062–5072 (2012).
Ni, K.-K. et al. A high phase-space-density gas of polar molecules. Science 322, 231–235 (2008).
Liu, Y., Grimes, D. D., Hu, M.-G. & Ni, K.-K. Probing ultracold chemistry using ion spectrometry. Phys. Chem. Chem. Phys. 22, 4861–4874 (2020).
Hu, M.-G. et al. Direct observation of bimolecular reactions of ultracold KRb molecules. Science 366, 1111–1115 (2019).
Hu, M.-G. et al. Nuclear spin conservation enables state-to-state control of ultracold molecular reactions. Nat. Chem. https://doi.org/10.1038/s41557-020-00610-0 (2020).
Byrd, J. N., Montgomery, J. A. Jr & Côté, R. Structure and thermochemistry of K2Rb, KRb2, and K2Rb2. Phys. Rev. A 82, 010502 (2010).
Yang, D. et al. A global full-dimensional potential energy surface for the K2Rb2 complex and its lifetime. J. Phys. Chem. Lett. 11, 2605–2610 (2020).
Liu, K. Product pair correlation in bimolecular reactions. Phys. Chem. Chem. Phys. 9, 17–30 (2007).
Brouard, M., O’Keeffe, P. & Vallance, C. Product state resolved dynamics of elementary reactions. J. Phys. Chem. A 106, 3629–3641 (2002).
Continetti, R. E. Coincidence spectroscopy. Annu. Rev. Phys. Chem. 52, 165–192 (2001).
Lee, S. K. et al. Coincidence ion imaging with a fast frame camera. Rev. Sci. Instrum. 85, 123303 (2014).
Wasserman, L. All Of Statistics: A Concise Course In Statistical Inference (Springer, 2004).
Meyer, E. R. & Bohn, J. L. Product-state control of bi-alkali-metal chemical reactions. Phys. Rev. A 82, 042707 (2010).
Amiot, C., Vergès, J. & Fellows, C. E.The long-range potential of the K2 \({X}^{1}{\Sigma }_{g}^{+}\) ground electronic state up to 15 Å. J. Chem. Phys. 103, 3350–3356 (1995).
Seto, J. Y., Le Roy, R. J., Verges, J. & Amiot, C. Direct potential fit analysis of the \({X}^{1}{\Sigma }_{g}^{+}\) state of Rb2: nothing else will do! J. Chem. Phys. 113, 3067–3076 (2000).
Yang, D., Huang, J., Hu, X., Xie, D. & Guo, H. Statistical quantum mechanical approach to diatom–diatom capture dynamics and application to ultracold KRb + KRb reaction. J. Chem. Phys. 152, 241103 (2020).
Brumer, P., Bergmann, K. & Shapiro, M. Identical collision partners in the coherent control of bimolecular reactions. J. Chem. Phys. 113, 2053–2055 (2000).
Kendrick, B., Hazra, J. & Balakrishnan, N. The geometric phase controls ultracold chemistry. Nat. Commun. 6, 7918 (2015).
Falke, S., Sherstov, I., Tiemann, E. & Lisdat, C. The \({A}^{1}{\Sigma }_{u}^{+}\) state of K2 up to the dissociation limit. J. Chem. Phys. 125, 224303 (2006).
Amiot, C. Laser-induced fluorescence of Rb2: the (1) \({}^{1}{\Sigma }_{g}^{+}(X)\), (2) \({}^{1}{\Sigma }_{g}^{+}\), (1) \({}^{1}{\Pi }_{u}(B)\), (1) \({}^{1}{\Pi }_{g}\), and (2) \({}^{1}{\Pi }_{g}(C)\) electronic states. J. Chem. Phys. 93, 8591–8604 (1990).
Aldegunde, J. & Hutson, J. M. Hyperfine energy levels of alkali-metal dimers: ground-state homonuclear molecules in magnetic fields. Phys. Rev. A 79, 013401 (2009).
Caldwell, C., Engelke, F. & Hage, H. High resolution spectroscopy in supersonic nozzle beams: the Rb2 \({B}^{1}{\Pi }_{u}-{X}_{1}{\Sigma }_{g}^{+}\) band system. Chem. Phys. 54, 21–31 (1980).
Amiot, C. & Vergès, J. Optical-optical double resonance and Fourier transform spectroscopy: the Rb2 \({B}_{1}{\Pi }_{u}\) electronic state up to the quasibound energy levels. Chem. Phys. Lett. 274, 91–98 (1997).
Ullrich, J. et al. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 66, 1463 (2003).
Vredenborg, A., Roeterdink, W. G. & Janssen, M. H. A photoelectron-photoion coincidence imaging apparatus for femtosecond time-resolved molecular dynamics with electron time-of-flight resolution of σ = 18 ps and energy resolution ΔE/E = 3.5%. Rev. Sci. Instrum. 79, 063108 (2008).
Eppink, A. T. & Parker, D. H. Velocity map imaging of ions and electrons using electrostatic lenses: application in photoelectron and photofragment ion imaging of molecular oxygen. Rev. Sci. Instrum. 68, 3477–3484 (1997).
Gericke, K.-H. Correlations between quantum state populations of coincident product pairs. Phys. Rev. Lett. 60, 561 (1988).
Lin, J. J., Zhou, J., Shiu, W. & Liu, K. State-specific correlation of coincident product pairs in the F + CD4 reaction. Science 300, 966–969 (2003).
Dixit, S., Levin, D. & McKoy, B. Resonant enhanced multiphoton ionization studies in atomic oxygen. Phys. Rev. A 37, 4220 (1988).
Johnson, B. An improved log derivative method for inelastic scattering. J. Comput. Phys. 13, 445−449 (1973).
Manolopoulos, D. An improved log derivative method for inelastic scattering. J. Chem. Phys. 85, 6425–6429 (1986).
Johnson, B. A generalized JWKB approximation for multichannel scattering. Chem. Phys. 2, 381–399 (1973).
Acknowledgements
We thank L. Zhu for experimental assistance; T. Rosenband, G. Quéméner, W. Cairncross, E. Heller and M. Soley for discussions; T. Karman for providing the code for state-counting; J. Huang for ab initio calculations; and L. Liu for a critical reading of the manuscript. This work is supported by the DOE Young Investigator Program (DE-SC0019020) and the David and Lucile Packard Foundation. M.A.N. is supported by the Arnold O. Beckman Postdoctoral Fellowship in Chemical Instrumentation. D.Y. and D.X. acknowledge support from the National Natural Science Foundation of China (grant numbers 21733006). H.G. thanks the Army Research Office (W911NF-19-1-0283) for funding.
Author information
Authors and Affiliations
Contributions
The experimental work and data analysis were carried out by Y.L., M.-G.H., M.A.N. and K.-K.N. Theoretical calculations were performed by D.Y., D.X. and H.G. All authors contributed to interpreting the results and writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Simon Cornish, Nandini Mukherjee and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Timing diagram for product ionization.
The relative timing between the ODT, REMPI, and cleanup pulses during the state-selective ionization of reaction products. The inset shows a close-up view of a single modulation period. Unperturbed reactions occur during the dark phase of the period, while reactions influenced by the (1,064 nm) ODT light occur during the bright phase. The numbers in parentheses indicate pulse durations.
Extended Data Fig. 2 Modelling the geometric factor for product sampling.
The plot shows the fraction of product pairs that remain within the REMPI beam volume at the time of ionization as a function of the velocity of the K2 product within the pair. Blue and red dashed lines indicate the maximum velocities of the K2 and Rb2 products, respectively. The inset shows the ionization geometry.
Extended Data Fig. 3 Modelling the Doppler factor for product sampling.
a, Normalized optical intensity profiles of the REMPI laser pulses. The red trace corresponds to the 648 nm or 674 nm lights, and is proportional to \({\varOmega }_{01}\). The green trace corresponds to the 532 nm light, and is proportional to \({\varGamma }_{{\rm{ion}}}\). b, The Doppler factor FDoppler(v) versus the velocity of the K2 product. The lower and upper bounds correspond to \({\varGamma }_{{\rm{i}}{\rm{o}}{\rm{n}}}/(2{\rm{\pi }})\) at peak values of 6 MHz and 14 MHz, respectively.
Extended Data Fig. 4 Distribution of product translational energy.
The measured (blue circle) and predicted (red diamond) scattering probabilities for all allowed state-pairs are plotted versus their translational energies (T). The two sets of points are offset horizontally by 0.014 cm−1 for clarity. To aid in the identification of systematic deviations, we multiply each scattering probability by a normalized Gaussian function with a 1σ width of 0.25 cm−1, and sum them up to construct broadened distributions as shown by the blue and red curves. These curves are scaled by a factor of 0.2 for convenience.
Rights and permissions
About this article
Cite this article
Liu, Y., Hu, MG., Nichols, M.A. et al. Precision test of statistical dynamics with state-to-state ultracold chemistry. Nature 593, 379–384 (2021). https://doi.org/10.1038/s41586-021-03459-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03459-6
This article is cited by
-
Raman sideband cooling of molecules in an optical tweezer array
Nature Physics (2024)
-
Many-body chemical reactions in a quantum degenerate gas
Nature Physics (2023)
-
Enhancing reactivity of SiO+ ions by controlled excitation to extreme rotational states
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.