Abstract
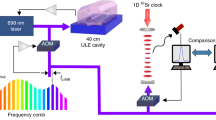
Microwave atomic clocks have traditionally served as the ‘gold standard’ for precision measurements of time and frequency. However, over the past decade, optical atomic clocks1,2,3,4,5,6 have surpassed the precision of their microwave counterparts by two orders of magnitude or more. Extant optical clocks occupy volumes of more than one cubic metre, and it is a substantial challenge to enable these clocks to operate in field environments, which requires the ruggedization and miniaturization of the atomic reference and clock laser along with their supporting lasers and electronics4,7,8,9. In terms of the clock laser, prior laboratory demonstrations of optical clocks have relied on the exceptional performance gained through stabilization using bulk cavities, which unfortunately necessitates the use of vacuum and also renders the laser susceptible to vibration-induced noise. Here, using a stimulated Brillouin scattering laser subsystem that has a reduced cavity volume and operates without vacuum, we demonstrate a promising component of a portable optical atomic clock architecture. We interrogate a 88Sr+ ion with our stimulated Brillouin scattering laser and achieve a clock exhibiting short-term stability of 3.9 × 10−14 over one second—an improvement of an order of magnitude over state-of-the-art microwave clocks. This performance increase within a potentially portable system presents a compelling avenue for substantially improving existing technology, such as the global positioning system, and also for enabling the exploration of topics such as geodetic measurements of the Earth, searches for dark matter and investigations into possible long-term variations of fundamental physics constants10,11,12.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets that support this study are available from the corresponding author on reasonable request.
Code availability
The codes used for analysis and simulations are available from the corresponding author on reasonable request.
References
Hinkley, N. et al. An atomic clock with 10−18 instability. Science 341, 1215–1218 (2013).
Bloom, B. J. et al. An optical lattice clock with accuracy and stability at the 10−18 level. Nature 506, 71–75 (2014).
Brewer, S. M. et al. 27Al+ quantum-logic clock with a systematic uncertainty below 10−18. Phys. Rev. Lett. 123, 033201 (2019).
Koller, S. B. et al. Transportable optical lattice clock with 7 × 10−17 uncertainty. Phys. Rev. Lett. 118, 073601 (2017).
Godun, R. M. et al. Frequency ratio of two optical clock transitions in 171Yb+ and constraints on the time variation of fundamental constants. Phys. Rev. Lett. 113, 210801 (2014).
Huntemann, N., Sanner, C., Lipphardt, B., Tamm, Chr. & Peik, E. Single-ion atomic clock with 3 × 10−18 systematic uncertainty. Phys. Rev. Lett. 116, 063001 (2016).
Leibrandt, D. R., Thorpe, M. J., Bergquist, J. C. & Rosenband, T. Field-test of a robust, portable, frequency-stable laser. Opt. Express 19, 10278–10286 (2011).
Liu, L. et al. In-orbit operation of an atomic clock based on laser-cooled 87Rb. Nat. Commun. 9, 2760 (2018).
Takamoto, M. et al. Test of general relativity by a pair of transportable optical lattice clocks. Nat. Photon. 14, 411–415 (2020).
Maleki, L. & Prestage, J. Applications of clocks and frequency standards: from the routine to tests of fundamental models. Metrologia 42, S145–S153 (2005).
Ludlow, A. D., Boyd, M. M., Ye, J., Peik, E. & Schmidt, P. O. Optical atomic clocks. Rev. Mod. Phys. 87, 637–701 (2015).
McGrew, W. F. et al. Atomic clock performance enabling geodesy below the centimetre level. Nature 564, 87–90 (2018).
Young, B. C., Cruz, F. C., Itano, W. M. & Bergquist, J. C. Visible lasers with subhertz linewidths. Phys. Rev. Lett. 82, 3799–3802 (1999).
Jiang, Y. Y. et al. Making optical atomic clocks more stable with 10−16-level laser stabilization. Nat. Photon. 5, 158–161 (2011).
Kessler, T. et al. A sub-40-mHz-linewidth laser based on a silicon single-crystal optical cavity. Nat. Photon. 6, 687–692 (2012).
Davila-Rodriguez, J. et al. Compact, thermal-noise-limited reference cavity for ultra-low-noise microwave generation. Opt. Lett. 42, 1277–1280 (2017).
Didier, A. et al. Ultracompact reference ultralow expansion glass cavity. Appl. Opt. 57, 6470–6473 (2018).
Grudinin, I. S., Matsko, A. B. & Maleki, L. Brillouin lasing with a CaF2 whispering gallery mode resonator. Phys. Rev. Lett. 102, 043902 (2009).
Lee, H. et al. Chemically etched ultrahigh-Q wedge-resonator on a silicon chip. Nat. Photon. 6, 369–373 (2012).
Kabakova, I. V. et al. Narrow linewidth Brillouin laser based on chalcogenide photonic chip. Opt. Lett. 38, 3208–3211 (2013).
Loh, W. et al. Dual-microcavity narrow-linewidth Brillouin laser. Optica 2, 225–232 (2015).
Otterstrom, N. T., Behunin, R. O., Kittlaus, E. A., Wang, Z. & Rakich, P. T. A silicon Brillouin laser. Science 360, 1113–1116 (2018).
Gundavarapu, S. et al. Sub-hertz fundamental linewidth photonic integrated Brillouin laser. Nat. Photon. 13, 60–67 (2019).
Geng, J. et al. Highly stable low-noise Brillouin fiber laser with ultranarrow spectral linewidth. IEEE Photonics Technol. Lett. 18, 1813–1815 (2006).
Shee, Y. G., Al-Mansoori, M. H., Ismail, A., Hitam, S. & Mahdi, M. A. Multiwavelength Brillouin-erbium fiber laser with double-Brillouin-frequency spacing. Opt. Express 19, 1699–1706 (2011).
Tow, K. H. et al. Linewidth-narrowing and intensity noise reduction of the 2nd order Stokes component of a low threshold Brillouin laser made of Ge10As22Se68 chalcogenide fiber. Opt. Express 20, B104–B109 (2012).
Debut, A., Randoux, S. & Zemmouri, J. Linewidth narrowing in Brillouin lasers: theoretical analysis. Phys. Rev. A 62, 023803 (2000).
Loh, W., Yegnanarayanan, S., O’Donnell, F. & Juodawlkis, P. W. Ultra-narrow linewidth Brillouin laser with nanokelvin temperature self-referencing. Optica 6, 152–159 (2019).
Jefferts, S. R., Meekhof, D. M., Shirley, J. H., Stepanovic, M. & Parker, T. E. Accuracy results from NIST-F1 laser-cooled cesium primary frequency standard. In Proc. IEEE/EIA Int. Frequency Control Symposium and Exhibition 714–717 (IEEE, 2000).
Madej, A. A., Dubé, P., Zhou, Z., Bernard, J. E. & Gertsvolf, M. 88Sr+ 445-THz single-ion reference at the 10−17 level via control and cancellation of systematic uncertainties and its measurement against the SI second. Phys. Rev. Lett. 109, 203002 (2012).
Strekalov, D. V., Thompson, R. J., Baumgartel, L. M., Grudinin, I. S. & Yu, N. Temperature measurement and stabilization in a birefringent whispering gallery mode resonator. Opt. Express 19, 14495–14501 (2011).
Fescenko, I. et al. Dual-mode temperature compensation technique for laser stabilization to a crystalline whispering gallery mode resonator. Opt. Express 20, 19185–19193 (2012).
Weng, W. et al. Nanokelvin thermometry and temperature control: beyond the thermal noise limit. Phys. Rev. Lett. 112, 160801 (2014).
Lim, J. et al. Probing 10 μK stability and residual drifts in the cross-polarization dual-mode stabilization of single-crystal ultrahigh-Q optical resonators. Light Sci. Appl. 8, 1 (2019).
Drever, R. W. P. et al. Laser phase and frequency stabilization using an optical resonator. Appl. Phys. B 31, 97–105 (1983).
Storz, R., Braxmaier, C., Jäck, K., Pradl, O. & Schiller, S. Ultrahigh long-term dimensional stability of a sapphire cryogenic optical resonator. Opt. Lett. 23, 1031–1033 (1998).
Bruzewicz, C. D., McConnell, R., Chiaverini, J. & Sage, J. M. Scalable loading of a two-dimensional trapped-ion array. Nat. Commun. 7, 13005 (2016).
Wang, S. X., Labaziewicz, J., Ge, Y., Shewmon, R. & Chuang, I. L. Demonstration of a quantum logic gate in a cryogenic surface-electrode ion trap. Phys. Rev. A 81, 062332 (2010).
Ma, L. S., Junger, P., Ye, J. & Hall, J. L. Delivering the same optical frequency at two places: accurate cancellation of phase noise introduced by an optical fiber or other time-varying path. Opt. Lett. 19, 1777–1779 (1994).
Nicholson, T. L. et al. Comparison of two independent Sr optical clocks with 1 × 10−17 stability at 103 s. Phys. Rev. Lett. 109, 230801 (2012).
Nicholson, T. L. et al. Systematic evaluation of an atomic clock at 2 × 10−18 uncertainty. Nat. Commun. 6, 6896 (2015).
Dubé, P. et al. Electric quadrupole shift cancellation in single-ion optical frequency standards. Phys. Rev. Lett. 95, 033001 (2005).
Spencer, D. T. et al. An optical frequency synthesizer using integrated photonics. Nature 557, 81–85 (2018).
Liang, W. et al. Ultralow noise miniature external cavity semiconductor laser. Nat. Commun. 6, 7371 (2015).
Zhang, W. et al. Ultranarrow linewidth photonic-atomic laser. Laser Photonics Rev. 14, 1900293 (2020).
Howe, D. A. The total deviation approach to long-term characterization of frequency stability. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 47, 1102–1110 (2000).
Chang, L. et al. Heterogeneous integration of lithium niobate and silicon nitride waveguides for wafer-scale photonic integrated circuits on silicon. Opt. Lett. 42, 803–806 (2017).
Hjelme, D. R., Mickelson, A. R. & Beausoleil, R. G. Semiconductor laser stabilization by external optical feedback. IEEE J. Quantum Electron. 27, 352–372 (1991).
Akerman, N., Navon, N., Kotler, S., Glickman, Y. & Ozeri, R. Universal gate-set for trapped-ion qubits using a narrow linewidth diode laser. New J. Phys. 17, 113060 (2015).
Cummins, H. K., Llewellyn, G. & Jones, J. A. Tackling systematic errors in quantum logic gates with composite rotations. Phys. Rev. A 67, 042308 (2003).
Acknowledgements
We thank A. Libson, G. N. West and I. L. Chuang for helpful discussions. This work was sponsored by the Under Secretary of Defense for Research and Engineering under Air Force contract number FA8721-05-C-0002. Opinions, interpretations, conclusions and recommendations are those of the authors and are not necessarily endorsed by the US Government.
Author information
Authors and Affiliations
Contributions
W.L., J.S. and R.M. conceived, designed and carried out the experiments with the SBS laser. W.L., J.S., D.R. and R.M. conceived, designed and carried out the experiments with the clock protocol. All authors discussed the results and contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Clément Lacroûte and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 SBS laser noise.
Shown is the measurement of the 674-nm SBS laser subsystem’s frequency noise before and after the application of feedforward stabilization. The SBS laser subsystem features a white noise floor of 3 Hz2 Hz−1 before feedforward and a gradual increase in noise at lower offset frequencies. An integration over the noise spectral density yields a full-width at half-maximum linewidth of 45 Hz, while a calculation of the white-noise limited linewidth at large offset frequencies yields 9 Hz. With feedforward turned on, the SBS laser subsystem’s noise increases slightly and exhibits additional noise peaks that arise from the RF signal generator used for feedforward correction. The integrated linewidth increases to 51 Hz.
Extended Data Fig. 2 Optimization of feedforward stabilization.
a, Measurement of the differential temperature sensitivity of the SBS resonator’s two orthogonal-polarization modes. The linewidths of the modes are measured to be 1.2 MHz (blue arrows). For an applied temperature shift of ΔT = −0.25 °C, the centre frequency at 1,348 nm changes by 490 MHz, while the mode separation (black arrows) changes by 11.9 MHz. This corresponds to a feedforward correction ratio of 40:1. b, Time series trace of the 1,348-nm SBS laser’s frequency with the linear drift removed and the SBS amplitude unservoed. The lack of correspondence between the free-running SBS (red trace) and the polarization beat note (‘Pol. beat ×39’; blue trace) indicates the inability to cancel frequency drift when amplitude noise is present.
Extended Data Fig. 3 Linear drift decay of SBS resonator.
Record of the SBS laser’s linear drift at 1,348 nm for two resonators. The first resonator (red circles) is tracked over 79 days, and its linear drift decreases to a value of 200 Hz s−1 at the end of the elapsed period of time. The second resonator (blue squares) is tracked over 260 days and reaches a minimum of 30 Hz s−1.
Extended Data Fig. 4 Determining and tracking linear drift.
a, Rabi spectroscopy of the |5S1/2, mJ = −1/2⟩ → |4D5/2, mJ = −3/2⟩ clock transition and the first-order motional sidebands at νclock ± νtrap (blue and red sideband, respectively) is taken at regular intervals of approximately 25 s. After performing fits to the symmetric sidebands, we can average the two frequencies to obtain an accurate measure of the frequency of the central feature. Only the spectroscopic data for the final experiment (black line) is shown; for all other datasets, the Gaussian peak fits to the sidebands (red and blue curves) are shown with progressively darkening colour to illustrate the movement of these features over time. For these data, an intentional linear drift of 5 kHz s−1 (at 674 nm; equivalently 2.5 kHz s−1 at 1,348 nm) was applied to demonstrate the efficacy of this method in cases of high drift, as in the initial few points shown in Extended Data Fig. 3. b, Rabi spectroscopy of the clock transition and sidebands after applying a linear drift correction to null out the natural drift of the resonator’s frequency. Over the course of 20 min of measurements, very little deviation in the centre frequency is observed. c, Linear drift determined from the data presented in b and c. The linear drift can be obtained from a fit (lines) to the apparent frequency of the clock transition as a function of time (data points). In the first case, with the large drift intentionally applied to the laser frequency, we obtain a drift of 5.2 kHz s−1 (at 674 nm) from the fit (green line). After a few iterations of applying a correction and measuring the resulting drift, the drift is driven down to 17 Hz s−1 (blue line). d, Integrated clock correction signal applied to the laser to keep the frequency resonant with the atom’s transition. In this case, we use a simplified clock protocol with an interrogation time of τ = 100 μs and no interleaving.
Extended Data Fig. 5 BCS laser 88Sr+ ion clock.
Measured interleaved clock performance comprising a BCS laser locked to a 88Sr+ ion operating with 1-ms interrogation time (blue points). The effective dead time is 4.7 ms. The blue points represent the frequency noise at a selection of averaging times, and the vertical blue bars indicate 1σ error. A fit (dashed line) to the data yields a stability of \(3.1\hspace{1pt}\times \hspace{1pt}{10}^{-14}/\sqrt{\tau }\), which is slightly lower than the same clock operated with a SBS laser.
Extended Data Fig. 6 Schematic of interleaved clock protocol.
A pictorial representation of the interleaved clock procedure is shown. Here the Doppler segments represent the 700-μs duration in which the ion is Doppler cooled. During the OP segments, the ion undergoes 450 μs of optical pumping in order to prepare the electron in the lower level of the clock transition. The ‘Interrogate’ segments are each 1 ms of interrogation time, bounded by composite π/2 pulses. Last, the ‘Detect’ segments are 700 μs of detection time, during which the photons emitted by the ion are detected on a photomultiplier tube and counted by our timing controller. During the ‘Update’ segment, and depending on the number of photons collected, the state of the ion is determined, and the frequency of the clock is either increased or decreased. As discussed in the text, two separate clock signals, f(1) and f(2), are maintained; here these are indicated as Clock 1 and Clock 2. While the frequency of either clock is updated, the experiment begins to prepare the state for the next measurement, as indicated by the black arrows. Each of these clocks is sensitive to laser frequency fluctuation only during the 1 ms interrogation period of the total 5.7 ms cycle time; during all other times, the frequency of the laser must stay within the capture range of the lock.
Extended Data Fig. 7 Numerical simulation of clock performance.
The measured performance of the stabilized SBS laser (Allan deviation, red curve) is used as an input into a clock protocol simulation incorporating projection noise and dead time. The simulation accurately predicts the measured clock performance via the interleaved self-comparison (green squares) and predicts a single-clock stability of \(2.5\hspace{1pt}\times \hspace{1pt}{10}^{-14}/\sqrt{\tau }\) (blue circles).
Rights and permissions
About this article
Cite this article
Loh, W., Stuart, J., Reens, D. et al. Operation of an optical atomic clock with a Brillouin laser subsystem. Nature 588, 244–249 (2020). https://doi.org/10.1038/s41586-020-2981-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2981-6
This article is cited by
-
Frequency comb-to-comb stabilization over a 1.3-km free-space atmospheric optical link
Light: Science & Applications (2022)
-
Large evanescently-induced Brillouin scattering at the surrounding of a nanofibre
Nature Communications (2022)
-
Visible light photonic integrated Brillouin laser
Nature Communications (2021)
-
Single-shot measurement of the photonic band structure in a fiber-based Floquet-Bloch lattice
Communications Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.