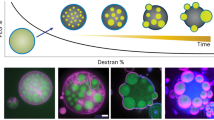
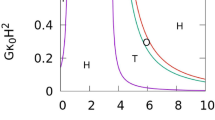
Abstract
Biological cells generate intricate structures by sculpting their membrane from within to actively sense and respond to external stimuli or to explore their environment1,2,3,4. Several pathogenic bacteria also provide examples of how localized forces strongly deform cell membranes from inside, leading to the invasion of neighbouring healthy mammalian cells5. Giant unilamellar vesicles have been successfully used as a minimal model system with which to mimic biological cells6,7,8,9,10,11, but the realization of a minimal system with localized active internal forces that can strongly deform lipid membranes from within and lead to dramatic shape changes remains challenging. Here we present a combined experimental and simulation study that demonstrates how self-propelled particles enclosed in giant unilamellar vesicles can induce a plethora of non-equilibrium shapes and active membrane fluctuations. Using confocal microscopy, in the experiments we explore the membrane response to local forces exerted by self-phoretic Janus microswimmers. To quantify dynamic membrane changes, we perform Langevin dynamics simulations of active Brownian particles enclosed in thin membrane shells modelled by dynamically triangulated surfaces. The most pronounced shape changes are observed at low and moderate particle loadings, with the formation of tether-like protrusions and highly branched, dendritic structures, whereas at high volume fractions globally deformed vesicle shapes are observed. The resulting state diagram predicts the conditions under which local internal forces generate various membrane shapes. A controlled realization of such distorted vesicle morphologies could improve the design of artificial systems such as small-scale soft robots and synthetic cells.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes used in this study are available from the corresponding authors upon reasonable request.
References
Mattila, P. K. & Lappalainen, P. Filopodia: molecular architecture and cellular functions. Nat. Rev. Mol. Cell Biol. 9, 446–454 (2008).
Fletcher, D. A. & Mullins, R. D. Cell mechanics and the cytoskeleton. Nature 463, 485–492 (2010).
Needleman, D. & Dogic, Z. Active matter at the interface between materials science and cell biology. Nat. Rev. Mater. 2, 17048 (2017).
Turlier, H. et al. Equilibrium physics breakdown reveals the active nature of red blood cell flickering. Nat. Phys. 12, 513–519 (2016).
Pizarro-Cerdá, J., Charbit, A., Enninga, J., Lafont, F. & Cossart, P. in Seminars in Cell & Developmental Biology Vol. 60, 155–167 (Elsevier, 2016).
Dimova, R. & Marques, C. The Giant Vesicle Book (CRC Press, 2019).
Keber, F. C. et al. Topology and dynamics of active nematic vesicles. Science 345, 1135–1139 (2014).
Mulla, Y., Aufderhorst-Roberts, A. & Koenderink, G. H. Shaping up synthetic cells. Phys. Biol. 15, 041001 (2018).
Steinkühler, J. et al. Controlled division of cell-sized vesicles by low densities of membrane-bound proteins. Nat. Commun. 11, 905 (2020).
Ganzinger, K. A. & Schwille, P. More from less—bottom-up reconstitution of cell biology. J. Cell Sci. 132, 227488 (2019).
Mellouli, S. et al. Self-organization of the bacterial cell-division protein Ftsz in confined environments. Soft Matter 9, 10493–10500 (2013).
Elgeti, J. & Gompper, G. Wall accumulation of self-propelled spheres. Eur. Phys. Lett. 101, 48003 (2013).
Fily, Y., Baskaran, A. & Hagan, M. F. Dynamics of self-propelled particles under strong confinement. Soft Matter 10, 5609 (2014).
Bechinger, C. et al. Active particles in complex and crowded environments. Rev. Mod. Phys. 88, 045006 (2016).
Gompper, G. et al. The 2019 motile active matter roadmap. J. Phys. Condens. Matter 32, 193001 (2020).
Paoluzzi, M., Di Leonardo, R., Marchetti, M. C. & Angelani, L. Shape and displacement fluctuations in soft vesicles filled by active particles. Sci. Rep. 6, 34146 (2016).
Wang, C., Guo, Y.-k., Tian, W.-d. & Chen, K. Shape transformation and manipulation of a vesicle by active particles. J. Chem. Phys. 150, 044907 (2019).
Li, Y. & ten Wolde, P. Shape transformations of vesicles induced by swim pressure. Phys. Rev. Lett. 123, 148003 (2019).
Kroll, D. & Gompper, G. The conformation of fluid membranes: Monte Carlo simulations. Science 255, 968 (1992).
Pécréaux, J., Döbereiner, H.-G., Prost, J., Joanny, J.-F. & Bassereau, P. Refined contour analysis of giant unilamellar vesicles. Eur. Phys. J. E 13, 277–290 (2004).
Heinrich, V. & Waugh, R. E. A piconewton force transducer and its application to measurement of the bending stiffness of phospholipid membranes. Ann. Biomed. Eng. 24, 595–605 (1996).
Cuvelier, D., Derenyi, I., Bassereau, P. & Nassoy, P. Coalescence of membrane tethers: experiments, theory, and applications. Biophys. J. 88, 2714–2726 (2005).
Takatori, S. C., Yan, W. & Brady, J. F. Swim pressure: stress generation in active matter. Phys. Rev. Lett. 113, 028103 (2014).
Manneville, J.-B., Bassereau, P., Lévy, D. & Prost, J. Activity of transmembrane proteins induces magnification of shape fluctuations of lipid membranes. Phys. Rev. Lett. 82, 4356–4359 (1999).
Takatori, S. C. & Sahu, A. Active contact forces drive nonequilibrium fluctuations in membrane vesicles. Phys. Rev. Lett. 124, 158102 (2020).
Park, Y. et al. Metabolic remodelling of the human red blood cell membrane. Proc. Natl Acad. Sci. USA 107, 1289–1294 (2010).
Natsume, Y. et al. Preparation of giant vesicles encapsulating microspheres by centrifugation of a water-in-oil emulsion. J. Vis. Exp. 119, e55282 (2017).
Song, J.-S., Tronc, F. & Winnik, M. A. Two-stage dispersion polymerization toward monodisperse, controlled micrometre-sized copolymer particles. J. Am. Chem. Soc. 126, 6562–6563 (2004).
Vutukuri, H. R., Bet, B., Van Roij, R., Dijkstra, M. & Huck, W. T. Rational design and dynamics of self-propelled colloidal bead chains: from rotators to flagella. Sci. Rep. 7, 16758 (2017).
Drabik, D., Przybyło, M., Chodaczek, G., Iglič, A. & Langner, M. The modified fluorescence based vesicle fluctuation spectroscopy technique for determination of lipid bilayer bending properties. Biochim. Biophys. Acta Biomembr. 1858, 244–252 (2016).
Yoon, Y.-Z. et al. Flickering analysis of erythrocyte mechanical properties: dependence on oxygenation level, cell shape, and hydration level. Biophys. J. 97, 1606–1615 (2009).
Bassereau, P., Sorre, B. & Lévy, A. Bending lipid membranes: experiments after W. Helfrich’s model. Adv. Colloid Interface Sci. 208, 47–57 (2014).
Frigo, M. & Johnson, S. G. The design and implementation of FFTW3. Proc. IEEE 93, 216–231 (2005).
Gompper, G. & Kroll, D. M. in Statistical Mechanics of Membranes and Surfaces 2nd edn (eds Nelson, D. R. et al.) 359–426 (World Scientific, 2004).
Noguchi, H. & Gompper, G. Dynamics of fluid vesicles in shear flow: effect of the membrane viscosity and thermal fluctuations. Phys. Rev. E 72, 011901 (2005).
Helfrich, W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C 28, 693–703 (1973).
Gompper, G. & Kroll, D. Random surface discretizations and the renormalization of the bending rigidity. J. Phys. I 6, 1305–1320 (1996).
Gompper, G. & Kroll, D. M. Network models of fluid, hexatic and polymerized membranes. J. Phys. Condens. Matter 9, 8795–8834 (1997).
Guckenberger, A. & Gekle, S. Theory and algorithms to compute Helfrich bending forces: a review. J. Phys. Condens. Matter 29, 203001 (2017).
Allen, M. P. & Tildesley, D. J. Computer Simulation of Liquids (Clarendon Press, 1991).
Noguchi, H. & Gompper, G. Fluid vesicles with viscous membranes in shear flow. Phys. Rev. Lett. 93, 258102 (2004).
Wysocki, A., Winkler, R. G. & Gompper, G. Cooperative motion of active Brownian spheres in three-dimensional dense suspensions. Eur. Phys. Lett. 105, 48004 (2014).
Stenhammar, J., Marenduzzo, D., Allen, R. J. & Cates, M. E. Phase behaviour of active Brownian particles: the role of dimensionality. Soft Matter 10, 1489–1499 (2014).
Acknowledgements
H.R.V. acknowledges financial support through a Marie Skłodowska-Curie Intra European Individual Fellowship (grant number 708349-SPCOLPS) within Horizon 2020. J.V. acknowledges financial support by the Swiss National Science Foundation (grant number 200021-165974). C.A.-V. acknowledges support by the International Helmholtz Research School of Biophysics and Soft Matter (IHRS BioSoft). G.G. acknowledges support by Deutsche Forschungsgemeinschaft (DFG) through the priority programme SPP1726 on ‘Microswimmers’. We thank P. Walde for discussions, N. Jaensson for initial help with membrane curve fitting in experiments and E. Spruijt for polystyrene particle synthesis. We gratefully acknowledge the computing time granted through JARA-HPC on the supercomputer JURECA at Forschungszentrum Jülich.
Author information
Authors and Affiliations
Contributions
H.R.V. and J.V. conceived and designed the project. H.R.V., L.v.B., and A.D. performed the experimental work. H.R.V. performed the experimental analysis. T.A., D.A.F. and G.G. designed the simulations. M.H. and D.A.F. performed 3D simulations. C.A.-V. performed 2D simulations. M.H., C.A.-V. and D.A.F. analysed the simulation data. M.H., C.A.-V, D.A.F. and T.A. performed the analytical calculations. All authors participated in the discussions, and H.R.V., T.A., D.A.F., G.G. and J.V. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Rumiana Dimova and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Encapsulation of colloids in giant DOPC vesicles.
a, Schematic representation of the working principle of the production of giant vesicles by using the droplet transfer method. b–d, Confocal microscopy images showing the lipid membrane and particles in GUVs. Passive isotropic particles in low-tension vesicles (c) and high-tension giant vesicles (d). Combined confocal and bright-field micrographs of Janus particles inside the GUVs of high-tension (e) and low-tension (f) vesicles. g–i, Sequence of time-lapse combined 2D confocal and bright-field microscopy images showing no specific interactions between the particles and the lipid membrane; as a result, no vesicle shape change is observed. The particle volume fraction is ϕ ≈ 0.23. Scale bars are 10.0 μm.
Extended Data Fig. 2 Cooperative budding and tubular confinement of SPPs.
Time-lapse of combined confocal and bright-field microscopy images showing the cooperative motion of SPPs inside the tether/channel of the lipid membrane. a–d, A flaccid vesicle first shows formation of a tether, which is transformed into a channel by multiple active particles. SPPs move into (a, b) and out of (c, d) the channel when they change propulsion direction. The inset shows a helical packing of active particles. The red arrow depicts the direction of the motion of the active particle into and out of the channel. The particle volume fraction is ≈3 × 10−3. e–j, Formation of a long (≈200 μm) tether extruded by a cluster of active particles (ten). Time-lapse images show the tubular confinement of a linear arrangement (inset of g) of individual active particles while the cluster of particles further pulls the membrane. h–j, The tether remains stable until its propulsion direction is reversed and the stored elastic energy counteracts the tether formation. As a result, the vesicle recovers its spherical shape. Scale bars are 10.0 μm.
Extended Data Fig. 3 State diagram of various membrane structures for a vesicle with a volume constraint.
a, Vesicle shapes for reduced volume v = 0.8 as a function of Pe and ϕ. Similar to the simulated diagram in Fig. 2a for a vesicle without a volume constraint, three regimes exist: tethering (blue symbols), fluctuating (red symbols) and bola/prolate (green symbols) vesicle shapes. The points corresponding to the snapshots have black outlines. The boundary (black lines) of the tethering regime from theoretical calculations is the same as in Fig. 2a. Interestingly, tether formation for v = 0.8 is present at Pe = 100, whereas without a volume constraint, tethers and daughter vesicles are observed only for Pe > 100. b, Simulations of vesicles deformed by active particles for reduced volume v = 0.6 at Pe = 50. The occurrence of protrusions at Pe = 50 demonstrates that low reduced volumes favour the formation of tethers or daughter vesicles.
Extended Data Fig. 4 Sizes and forces of active particle clusters.
a, Size distributions of clusters formed by active particles for various Pe and ϕ values from simulations with reduced volume v = 0.8. Larger clusters form at higher volume fractions of active particles and at larger Pe. The tails of the cluster size distributions follow a nearly exponential decay. b, Average cluster forces in the direction of the membrane for various Pe and ϕ values. The average force is a nearly linear function of the cluster size Np,c, such that it can be approximated as fp,c = βNp,cfp, where β is the cooperativity coefficient, which weakly depends on Pe. Linear fitting of the fp,c data results in β ≈ 0.3 for Pe = 25, β ≈ 0.4 for Pe = 50 and β ≈ 0.54 for Pe = 100.
Extended Data Fig. 5 Vesicle morphologies at higher particle loadings.
Vesicle topology changes are observed at high volume fraction of particles. Scale bars are 10.0 μm.
Extended Data Fig. 6 Fluctuations of 2D vesicles.
a, b, Fluctuation spectra for vesicles with enclosed active particles of various Pe at area fraction ϕ′ = 0.12 without (a) and with (b) an area constraint. The insets show the exponents obtained using power-law fits to ℓ−α, measured in the ranges 10 ≤ ℓ ≤ 17 for α1 and 35 ≤ ℓ ≤ 50 for α2. c, d, Fluctuation spectra of active vesicles at Pe = 75 for various volume fractions ϕ′ without (c) and with (d) an area constraint. e, f, PDFs for fluctuations of the radial position of the vesicle contour around its average position for rings without (e) and with (f) an area constraint. The data denoted by ϕ′ = 0 are for the passive system.
Extended Data Fig. 7 Theoretical phase diagrams for tether formation by active particles for two passive membrane tensions λp.
a, Tether boundaries for various cluster cooperativities β. At low ϕ, equation (19) with ⟨Np,c⟩ = 1, β = 1 and σcl = σ is employed, whereas at large ϕ, ⟨Np,c⟩ and σcl are functions of the number Np of active particles. In all cases, the active-tension weight is set to γ = 0.25. b, Tether boundaries for different spontaneous curvatures c0. Here, λp = 2 × 10−8 N m−1. Tethers are predicted to occur at high enough Pe and for small volume fractions ϕ of active particles. A non-zero spontaneous curvature of the membrane can substantially reduce the propulsion force needed to form a tether.
Supplementary information
Supplementary Information
This file contains Supplementary Methods, two Supplementary Discussions, one Supplementary Figure, and Supplementary References.
Supplementary Video 1: Dynamic response of lipid membrane to SPPs in giant vesicles
Time-lapsed overlaid 2D confocal and bright-field microscopy videos: Left panel shows SPPs at a low volume fraction (ϕ ≈ 10−4) in a low-tension vesicle. A sequence of dynamic processes is observed where particles first propel freely and when in contact with the membrane long enough they go from a partial to a full wrapping state by the membrane, which is followed by budding and tethering. The right panel shows SPPs in a high-tension vesicle. Particles follow the curvature and make circles. Note that the propulsion speed of the SPPs in both cases are same. Both videos were recorded 1 min after the fuel addition. The video is accelerated by 2×.
Supplementary Video 2: Global shape change
This video shows the effect of volume fraction of SPPs on the dynamic response of the membrane of a low-tension vesicle. At high particle loadings (ϕ ≈ 0.19), global shape changes of a vesicle are observed. This video was recorded 2 mins after the fuel addition. The video is accelerated by 2×.
Supplementary Video 3: Activity-induced vesicle shapes
Vesicle tethering facilitated by single SPPs from 3D simulations for Pe = 800 and ϕ = 2.2 × 10−3 (or Np = 9). A local force from the SPPs exerted on the membrane is so large that they quickly form several separate tethers.
Supplementary Video 4: Astrocyte-like shape
Formation of an astrocyte-like shape from 3D simulations for Pe = 200 and ϕ = 2 × 10−2 (or Np = 81). Note that the initial formation of tethers is performed by clusters of several SPPs, after which they grow into very long membrane protrusions.
Supplementary Video 5: Global shape change
A vesicle simulated for Pe = 200 and ϕ = 1.8 × 10−1(or Np = 729). First, the initially spherical vesicle is deformed into an elongated shape by two large clusters of SPPs. Then, a dumbbell-like structure is formed.
Supplementary Video 6: Activity-induced tension
Dynamic response of a low-tension vesicle to particles with a high propulsion speed (vp ≈ 21 µm s−1). A cluster of SPPs triggers initially tether formation, then channelling followed by the formation of daughter vesicles that are still connected to the mother vesicle, eventually leading to the activity-induced membrane tension. This video was recorded 1 min after the fuel addition. The video is accelerated by 1.5×.
Rights and permissions
About this article
Cite this article
Vutukuri, H.R., Hoore, M., Abaurrea-Velasco, C. et al. Active particles induce large shape deformations in giant lipid vesicles. Nature 586, 52–56 (2020). https://doi.org/10.1038/s41586-020-2730-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2730-x
This article is cited by
-
Mesoscale simulation of biomembranes with FreeDTS
Nature Communications (2024)
-
The crucial role of adhesion in the transmigration of active droplets through interstitial orifices
Nature Communications (2023)
-
Scaling behaviour and control of nuclear wrinkling
Nature Physics (2023)
-
A colloidal viewpoint on the sausage catastrophe and the finite sphere packing problem
Nature Communications (2023)
-
Versatile synthesis of metal-compound based mesoporous Janus nanoparticles
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.