Abstract
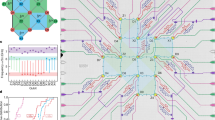
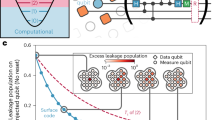
The successful operation of quantum computers relies on protecting qubits from decoherence and noise, which—if uncorrected—will lead to erroneous results. Because these errors accumulate during an algorithm, correcting them is a key requirement for large-scale and fault-tolerant quantum information processors. Besides computational errors, which can be addressed by quantum error correction1,2,3,4,5,6,7,8,9, the carrier of the information can also be completely lost or the information can leak out of the computational space10,11,12,13,14. It is expected that such loss errors will occur at rates that are comparable to those of computational errors. Here we experimentally implement a full cycle of qubit loss detection and correction on a minimal instance of a topological surface code15,16 in a trapped-ion quantum processor. The key technique used for this correction is a quantum non-demolition measurement performed via an ancillary qubit, which acts as a minimally invasive probe that detects absent qubits while imparting the smallest quantum mechanically possible disturbance to the remaining qubits. Upon detecting qubit loss, a recovery procedure is triggered in real time that maps the logical information onto a new encoding on the remaining qubits. Although the current demonstration is performed in a trapped-ion quantum processor17, the protocol is applicable to other quantum computing architectures and error correcting codes, including leading two- and three-dimensional topological codes. These deterministic methods provide a complete toolbox for the correction of qubit loss that, together with techniques that mitigate computational errors, constitute the building blocks of complete and scalable quantum error correction.
This is a preview of subscription content, access via your institution
Relevant articles
Open Access articles citing this article.
-
Experimental demonstration of continuous quantum error correction
Nature Communications Open Access 28 April 2022
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 per month
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Get just this article for as long as you need it
$39.95
Prices may be subject to local taxes which are calculated during checkout
Data availability
The data underlying the findings of this work are available at https://doi.org/10.5281/zenodo.3900057. Source data are provided with this paper.
Code availability
All codes used for data analysis are available from the corresponding author upon reasonable request.
References
Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004).
Schindler, P. et al. Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011).
Nigg, D. et al. Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014).
Takita, M., Cross, A. W., Córcoles, A. D., Chow, J. M. & Gambetta, J. M. Experimental demonstration of fault-tolerant state preparation with superconducting qubits. Phys. Rev. Lett. 119, 180501 (2017).
Linke, N. M. et al. Fault-tolerant quantum error detection. Sci. Adv. 3, e1701074 (2017).
Córcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
Knill, E., Laflamme, R., Martinez, R. & Negrevergne, C. Benchmarking quantum computers: the five-qubit error correcting code. Phys. Rev. Lett. 86, 5811 (2001).
Yao, X.-C. et al. Experimental demonstration of topological error correction. Nature 482, 489 (2012).
Grassl, M., Beth, T. & Pellizzari, T. Codes for the quantum erasure channel. Phys. Rev. A 56, 33–38 (1997).
Brown, N. C. & Brown, K. R. Comparing Zeeman qubits to hyperfine qubits in the context of the surface code: 174Yb+ and 171Yb+. Phys. Rev. A 97, 052301 (2018).
Lu, C.-Y. et al. Experimental quantum coding against qubit loss error. Proc. Natl Acad. Sci. USA 105, 11050–11054 (2008).
Bell, B. A. et al. Experimental demonstration of a graph state quantum error-correction code. Nat. Commun. 5, 3658 (2014).
Morley-Short, S. et al. Physical-depth architectural requirements for generating universal photonic cluster states. Quant. Sci. Tech. 3, 015005 (2018).
Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Dennis, E., Kitaev, A., Landahl, A. & Preskill J. Topological quantum memory. J. Math. Phys. 43, 4452 (2002).
Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013).
Fowler, A. G. Coping with qubit leakage in topological codes. Phys. Rev. A 88, 042308 (2013).
Epstein, J. M., Cross, A. W., Magesan, E. & Gambetta, J. M. Investigating the limits of randomized benchmarking protocols. Phys. Rev. A 89, 062321 (2014).
Xia, T. et al. Randomized benchmarking of single-qubit gates in a 2D array of neutral-atom qubits. Phys. Rev. Lett. 114, 100503 (2015).
Kwon, M., Ebert, M. F., Walker, T. G. & Saffman, M. Parallel low-loss measurement of multiple atomic qubits. Phys. Rev. Lett. 119, 180504 (2017).
Brown, N. C. & Brown, K. R. Leakage mitigation for quantum error correction using a mixed qubit scheme. Phys. Rev. A 100, 032325 (2019).
Hayes, D. et al. Eliminating leakage errors in hyperfine qubits. Phys. Rev. Lett. 124, 170501 (2020).
Ghosh, J., Fowler, A. G., Martinis, J. M. & Geller, M. R. Understanding the effects of leakage in superconducting quantum-error-detection circuits. Phys. Rev. A 88, 062329 (2013).
Stace, T. M., Barrett, S. D. & Doherty, A. C. Thresholds for topological codes in the presence of loss. Phys. Rev. Lett. 102, 200501 (2009).
Varbanov, B. M. et al. Leakage detection for a transmon-based surface code. Preprint at https://arxiv.org/abs/2002.07119 (2020).
Bombin, H. & Martin-Delgado, M. A. Topological quantum distillation. Phys. Rev. Lett. 97, 180501 (2006).
Vodola, D., Amaro, D., Martin-Delgado, M. A. & Müller, M. Twins percolation for qubit losses in topological color codes. Phys. Rev. Lett. 121, 060501 (2018).
Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1996).
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Mølmer, K. & Sørensen, A. Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835–1838 (1999).
Choi, M.-D. Completely positive linear maps on complex matrices. Linear Algebra Appl. 10, 285–290 (1975).
Knill, E. Quantum computing with realistically noisy devices. Nature 434, 39–44 (2005).
Aliferis, P., Gottesman, D. & Preskill, J. Quantum accuracy threshold for concatenated distance-3 codes. Quantum Inf. Comput. 6, 97–165 (2006).
Acknowledgements
We gratefully acknowledge funding by the US Army Research Office (ARO) through grant number W911NF-14-1-0103. We also acknowledge funding by the Austrian Science Fund (FWF), through the SFB BeyondC (FWF Project number F71), by the Austrian Research Promotion Agency (FFG) contract 872766, by the EU H2020-FETFLAG-2018-03 under Grant Agreement number 820495, and by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via US ARO Grant number W911NF-16-1-0070. All statements of fact, opinions or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of ODNI, the IARPA, or the US Government. We acknowledge support from the Samsung Advanced Institute of Technology Global Research Outreach. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement number 801110 and the Austrian Federal Ministry of Education, Science and Research (BMBWF). The information provided in this Article reflects only the authors’ views; the EU Agency is not responsible for any use that may be made of this information.
Author information
Authors and Affiliations
Contributions
D.V. and M. Müller derived the theory results. R.S., A.E., L.P., M. Meth, M.R., P.S. and T.M. performed the experiments. R.S. analysed the data. T.M., M. Müller and R.B. supervised the project. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Tom Stace and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Sections 1–5, which contain further experimental and theoretical results and details on the detection and correction of qubit loss. It includes Supplementary Figures 1–6 and Supplementary Tables 1–3.
Source data
Rights and permissions
About this article
Cite this article
Stricker, R., Vodola, D., Erhard, A. et al. Experimental deterministic correction of qubit loss. Nature 585, 207–210 (2020). https://doi.org/10.1038/s41586-020-2667-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2667-0
This article is cited by
-
Experimental demonstration of continuous quantum error correction
Nature Communications (2022)
-
Entangling logical qubits with lattice surgery
Nature (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
