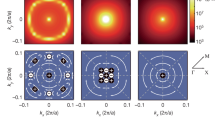
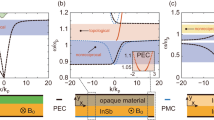
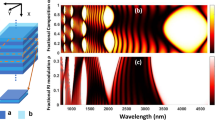
Abstract
Unidirectional radiation is important for various optoelectronic applications, such as lasers, grating couplers and optical antennas. However, almost all existing unidirectional emitters rely on the use of materials or structures that forbid outgoing waves—that is, mirrors, which are often bulky, lossy and difficult to fabricate. Here we theoretically propose and experimentally demonstrate a class of resonances in photonic crystal slabs that radiate only towards one side of the slab, with no mirror placed on the other side. These resonances, which we name ‘unidirectional guided resonances’, are found to be topological in nature: they emerge when a pair of half-integer topological charges1,2,3 in the polarization field bounce into each other in momentum space. We experimentally demonstrate unidirectional guided resonances in the telecommunication regime by achieving single-side radiative quality factors as high as 1.6 × 105. We further demonstrate their topological nature through far-field polarimetry measurements. Our work represents a characteristic example of applying topological principles4,5 to control optical fields and could lead to energy-efficient grating couplers and antennas for light detection and ranging.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The datasets generated and analysed during the current study are available from the corresponding author upon request.
References
Mermin, N. D. The topological theory of defects in ordered media. Rev. Mod. Phys. 51, 591–648 (1979).
Zhen, B., Hsu, C. W., Lu, L., Stone, A. D. & Soljačić, M. Topological nature of optical bound states in the continuum. Phys. Rev. Lett. 113, 257401 (2014).
Gbur, G. J. Singular Optics (CRC Press, 2016).
Lu, L., Joannopoulos, J. D. & Soljai, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Hsu, C. W., Zhen, B., Stone, A. D., Joannopoulos, J. D. & Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 1, 16048 (2016).
von Neuman, J. & Wigner, E. Über merkwürdige diskrete Eigenwerte. Über das Verhalten von Eigenwerten bei adiabatischen Prozessen. Phys. Z. 30, 467–470 (1929).
Friedrich, H. & Wintgen, D. Interfering resonances and bound states in the continuum. Phys. Rev. A 32, 3231–3242 (1985).
Fan, S. & Joannopoulos, J. D. Analysis of guided resonances in photonic crystal slabs. Phys. Rev. B 65, 235112 (2002).
Plotnik, Y. et al. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 107, 183901 (2011).
Hsu, C. W. et al. Observation of trapped light within the radiation continuum. Nature 499, 188–191 (2013).
Corrielli, G., Della Valle, G., Crespi, A., Osellame, R. & Longhi, S. Observation of surface states with algebraic localization. Phys. Rev. Lett. 111, 220403 (2013).
Kodigala, A. et al. Lasing action from photonic bound states in continuum. Nature 541, 196–199 (2017).
Gomis-Bresco, J., Artigas, D. & Torner, L. Anisotropy-induced photonic bound states in the continuum. Nat. Photon. 11, 232–236 (2017).
Molina, M. I., Miroshnichenko, A. E. & Kivshar, Y. S. Surface bound states in the continuum. Phys. Rev. Lett. 108, 070401 (2012).
Carletti, L., Koshelev, K., De Angelis, C. & Kivshar, Y. Giant nonlinear response at the nanoscale driven by bound states in the continuum. Phys. Rev. Lett. 121, 033903 (2018).
Monticone, F. & Alù, A. Embedded photonic eigenvalues in 3D nanostructures. Phys. Rev. Lett. 112, 213903 (2014).
Liu, Z. et al. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett. 123, 253901 (2019).
Lim, T. C. & Farnell, G. W. Character of pseudo surface waves on anisotropic crystals. J. Acoust. Soc. Am. 45, 845–851 (1969).
Cobelli, P. J., Pagneux, V., Maurel, A. & Petitjeans, P. Experimental observation of trapped modes in a water wave channel. Europhys. Lett. 88, 20006 (2009).
Hirose, K. et al. Watt-class high-power, high-beam-quality photonic-crystal lasers. Nat. Photon. 8, 406 (2014).
Chow, E., Grot, A., Mirkarimi, L. W., Sigalas, M. & Girolami, G. Ultracompact biochemical sensor built with two-dimensional photonic crystal microcavity. Opt. Lett. 29, 1093–1095 (2004).
Bulgakov, E. N. & Maksimov, D. N. Topological bound states in the continuum in arrays of dielectric spheres. Phys. Rev. Lett. 118, 267401 (2017).
Zhang, Y. et al. Observation of polarization vortices in momentum space. Phys. Rev. Lett. 120, 186103 (2018).
Doeleman, H. M., Monticone, F., den Hollander, W., Andrea, A. & Koenderink, A. F. Experimental observation of a polarization vortex at an optical bound state in the continuum. Nat. Photon. 12, 397–401 (2018).
Yang, Y., Peng, C., Liang, Y., Li, Z. & Noda, S. Analytical perspective for bound states in the continuum in photonic crystal slabs. Phys. Rev. Lett. 113, 037401 (2014).
Zhou, H. et al. Perfect single-sided radiation and absorption without mirrors. Optica 3, 1079–1086 (2016).
Wang, K. X., Yu, Z., Sandhu, S. & Fan, S. Fundamental bounds on decay rates in asymmetric single-mode optical resonators. Opt. Lett. 38, 100–102 (2013).
Liu, W. et al. Circularly polarized states spawning from bound states in the continuum. Phys. Rev. Lett. 123, 116104 (2019).
Jin, J. et al. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering. Nature 574, 501–504 (2019).
Zhou, H. et al. Observation of bulk Fermi arc and polarization half charge from paired exceptional points. Science 359, 1009–1012 (2018).
Wang, Z. et al. Mode splitting in high-index-contrast grating with mini-scale finite size. Opt. Lett. 41, 3872–3875 (2016).
Lv, J. et al. Demonstration of a thermo-optic phase shifter by utilizing high-Q resonance in high-index-contrast grating. Opt. Lett. 43, 827–830 (2018).
Regan, E. C. et al. Direct imaging of isofrequency contours in photonic structures. Sci. Adv. 2, e1601591 (2016).
McMaster, W. H. Polarization and the stokes parameters. Am. J. Phys. 22, 351–362 (1954).
Notaros, J. et al. Ultra-efficient CMOS fiber-to-chip grating couplers. In Optical Fiber Communications Conf. Exhib. 1–3 (IEEE, 2016).
Wade, M. T. et al. 75% efficient wide bandwidth grating couplers in a 45 nm microelectronics cmos process. In IEEE Optical Interconnects Conf. 46–47 (IEEE, 2015).
Wang, B., Jiang, J. & Nordin, G. P. Compact slanted grating couplers. Opt. Express 12, 3313–3326 (2004).
Li, M. & Sheard, S. J. Waveguide couplers using parallelogramic-shaped blazed gratings. Opt. Commun. 109, 239–245 (1994).
Hagberg, M., Eriksson, N. & Larsson, A. Investigation of high-efficiency surface-emitting lasers with blazed grating outcouplers. IEEE J. Quantum Electron. 32, 1596–1605 (1996).
Eriksson, N., Hagberg, M. & Larsson, A. Highly directional grating outcouplers with tailorable radiation characteristics. IEEE J. Quantum Electron. 32, 1038–1047 (1996).
Notaros, J. & Popovi, M. A. Band-structure approach to synthesis of grating couplers with ultra-high coupling efficiency and directivity. In Optical Fiber Communications Conf. Exhib. 1–3 (IEEE, 2015).
Michaels, A. & Yablonovitch, E. Inverse design of near unity efficiency perfectly vertical grating couplers. Opt. Express 26, 4766–4779 (2018).
Dai, M. et al. Highly efficient and perfectly vertical chip-to-fiber dual-layer grating coupler. Opt. Express 23, 1691–1698 (2015).
Acknowledgements
We thank L. He for discussion, V. Yoshioka for reading the manuscript and Z. Zhang for helping to conduct the experiments. C.P. was supported by the National Natural Science Foundation of China under grant number 61922004. J.J. and B.Z. were sponsored by the US Army Research Office under grant number W911NF-19-1-0087. The simulations were supported by the High-performance Computing Platform of Peking University. The project was partially supported by AFRL contract FA8650-16-D-5403 and MIT Lincoln Laboratory contract 7000371273, as well as by the Army Research Office, and was accomplished under Cooperative Agreement number W911NF-18-2-0048. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
Author information
Authors and Affiliations
Contributions
All authors contributed substantially to this work. X.Y., C.P. and B.Z. wrote the manuscript with contributions from all authors. M.S., C.P. and B.Z. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Yuri Kivshar, Mikael Rechtsman and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Sample fabrication.
a, Step-by-step flow chart of the fabrication process. b, Schematics of the customized RIE process. EBL, electron-beam lithography; PECVD, plasma-enhanced chemical vapour deposition; CMP, chemical-mechanical polishing.
Extended Data Fig. 2 Experimental setup used to measure the asymmetry ratio η.
The setup is capable of both near- and far-field measurements. The focal lengths of lenses L2, L3, L4 and L5 are 150 mm, 100 mm, 75 mm and 75 mm, respectively. RFP, rear focal plane; PD, photodetector; Obj, objective; Pol, polarizer; Amp, amplifier; BS, beam splitter. N1 and N2 denote the movable lenses used to achive near-field imaging.
Extended Data Fig. 3 Experimental and simulation results for disordered samples.
a, Experimentally extracted Qtot (blue) compared with simulation results for samples with (green) and without (red) disorder. b, Measured asymmetry ratio η (blue) compared with simulation results for samples with (green) and without (red) disorder.
Extended Data Fig. 4 Experimental setup used for polarimetry measurements.
An amplified spontaneous emission (ASE) source excites the resonances in the sample. Scattered light is recorded by a camera under six different combinations of a polarizer (Pol) and a QWP. The focal lengths of lenses L2, L3, L4 and L5 are 150 mm, 100 mm, 75 mm and 75 mm, respectively.
Extended Data Fig. 5 Experimental observation of the evolution of half-integer charges.
a, UGR as the merging point between two half-integer charges. b–f, Measured ellipticity ρ of the resonances in five samples with slightly different air-gap widths w, ranging from w/a = 0.399 (b) to 0.403 (f). Dark red (ρ = 1) and dark green (ρ = −1) colours indicate the locations of the LCP and RCP resonances, which are also half-integer topological charges.
Extended Data Fig. 6 Robustness of UGRs against parameter variations.
a, Device performance when the air-gap widths deviate by ±2.5 nm from the perfect design. b, Device performance when the etching angle deviates by ±1° from the perfect design (grey). c, The UGR is restored if the etching angle deviates by −1° from the perfect design and the air-gap width changes to w = 365 nm.
Extended Data Fig. 7 Asymmetry ratio for modes near UGRs.
Simulated (left) and measured (right) asymmetry ratios η for resonances close to the UGR in momentum space.
Extended Data Fig. 8 Prospects of using UGRs as grating couplers.
a, Asymmetry ratio η between upward and downward radiation intensities for a fixed out-coupling angle of 9°. The maximum reaches 27.7 dB near the UGR and remains high (above 10 dB) over a bandwidth of 26 nm. b, Highly directional emission is observed over a wide range of excitation wavelengths and for different out-coupling angles. The fibre-to-waveguide loss is not measured.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Supplementary Figures S1-S6.
Rights and permissions
About this article
Cite this article
Yin, X., Jin, J., Soljačić, M. et al. Observation of topologically enabled unidirectional guided resonances. Nature 580, 467–471 (2020). https://doi.org/10.1038/s41586-020-2181-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2181-4
This article is cited by
-
Observation of spatiotemporal optical vortices enabled by symmetry-breaking slanted nanograting
Nature Communications (2024)
-
Boundary-localized many-body bound states in the continuum
Communications Physics (2024)
-
Bound states in the continuum in divided triangular hole metasurfaces
Scientific Reports (2024)
-
Finite barrier bound state
Light: Science & Applications (2024)
-
Spin-valley Rashba monolayer laser
Nature Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.