Introduction

When pouring water into a cup, surface tension allows us to pour slightly more water than the cup’s volume can contain. Somewhat similarly, in 1998, Ebbesen et al. discovered that the energy transmitted through hole arrays could exceed the incident-on-the-holes-only energy, i.e., normalized transmission > 1, a phenomenon known as extraordinary optical transmission (EOT)1. Surface plasmon polaritons were used to explain this phenomenon: EOT results from an interaction between electrons on the metal surface and the electromagnetic wave at the exit end, leading to the excitation of surface plasmon polaritons. These excitations too contribute to the transmission through a hole, as a result of which when one normalizes the transmission (T) with the power directly incident (from free space) on a hole, this normalized T can exceed unity. The phenomenon of EOT has attracted great attention in the fields of plasmonics, metamaterials, and metasurfaces, particularly in the visible2,3 and infrared bands4,5,6, and has been exploited for many practical applications7,8.

More recently, the field of topological photonics has emerged9, allowing for unique degrees of control on the propagation of light waves. This field is of wider interest because it allows for robust transport, largely immune to deleterious structural defects and roughnesses, as well as for the excitation of rigorously one-way (unidirectional, nonreciprocal) waves, with no back-reflections or -scattering10. Furthermore, the bandwidth of the topological band in such structures is solely determined by topological arguments, allowing for broadband (nonresonant) operation at a targeted spectral regime11.

As we shall see in the following, these inherent properties of topological and nonreciprocal structures are also of interest for EOT devices. Indeed, most currently proposed EOT structures rely on complex artificial hole/slit arrays12,13 or tapered configurations14,15, which exhibit the EOT phenomenon only around certain operating frequencies—and with low-throughput efficiency, particularly for single-hole devices, ubiquitous in micro-/nano-scopy16. Although some studies have shown that EOT can also be observed in single-aperture geometries, such as the ‘Bull’s eyes’ configuration17, the exact EOT condition is fulfilled only at a given single frequency, owing to strict interference/resonance/coupling conditions, giving rise to normalized transmittance typically below unity beyond that frequency. Furthermore, traditional EOT structures are sensitive to structural defects or imperfections, requiring high-precision device fabrication.

Because of these phenomena, the throughput efficiency via single deep-subwavelength (or subdiffraction) holes is typically very small—e.g., in the case of near-field scanning optical microscopes, which is the incumbent technology for bringing light to the nanoscale, the throughput via a single hole with a surface 50 times smaller than the squared wavelength can be as low as 10−5, or less8,16.

Topological electromagnetic modes, particularly one-way modes, can help address these seemingly fundamental issues. In this Letter, we focus on the terahertz regime and introduce topological or nonreciprocal single-hole three-dimensional (3D) EOT devices that can be useful for diverse applications in the broader field of photonics. We note that achieving truly topologically one-way modes-based EOT in this range is challenging due to the presence of nonlocal effects18,19,20—a critical issue that is thoroughly analyzed and addressed herein. Previously, we reported two-dimensional (2D) nonreciprocal EOT structures based on localized (unidirectional) surface magnetoplasmons (SMPs) in straight magneto-optical heterostructures21. However, those studies were merely two-dimensional (i.e., they were concerning slits rather than 3D holes), did not include nonlocal effects, the involved structures with assumed infinite thickness were challenging to realize, and most importantly they did not attain (even in the absence of nonlocal effects) the EOT throughput performance reported later in this paper.

Results and discussion

Nonreciprocal SMPs under local and nonlocal conditions

In the beginning, we study two classic heterostructures: One composed of InSb and a dielectric material (such as silicon), and the other composed of InSb and an opaque material (OM) with a larger plasma frequency than InSb (e.g., \({\omega }_{{{{{{{{\rm{p}}}}}}}}}^{{{{{{{{\rm{m}}}}}}}}}=2{\omega }_{{{{{{{{\rm{p}}}}}}}}}\))18. We chose InSb, a magnetized semiconductor, in all three of the following structures because of its anisotropic permittivity tensor. When the magnetization direction is –z, the permittivity tensor can be written as

$$\overleftrightarrow{\varepsilon }=\left[\begin{array}{ccc}{\varepsilon }_{1}&-i{\varepsilon }_{2}&0\\ i{\varepsilon }_{2}&{\varepsilon }_{1}&0\\ 0&0&{\varepsilon }_{3}\end{array}\right]$$
(1)

where \({\varepsilon }_{1}={\varepsilon }_{\infty }\left\{1-\frac{(\omega +i\gamma ){\omega }_{{{{{{{{\rm{p}}}}}}}}}^{2}}{\omega \left[{(\omega +i\gamma )}^{2}-{\omega }_{{{{{{{{\rm{c}}}}}}}}}^{2}\right]}\right\}\), \({\varepsilon }_{2}={\varepsilon }_{\infty }\frac{{\omega }_{{{{{{{{\rm{c}}}}}}}}}{\omega }_{{{{{{{{\rm{p}}}}}}}}}^{2}}{\omega \left[{(\omega +i\gamma )}^{2}-{\omega }_{{{{{{{{\rm{c}}}}}}}}}^{2}\right]}\) and \({\varepsilon }_{3}={\varepsilon }_{\infty }\left\{1-\frac{{\omega }_{{{{{{{{\rm{p}}}}}}}}}^{2}}{\omega (\omega +{{{{{{{\rm{i\gamma }}}}}}}})}\right\}\). ωc = eB0/m*, ε∞, ωp = 4π × 1012 rad/s, and γ are the electron cyclotron frequency related to the external magnetic field, the high-frequency permittivity, the plasma frequency, and the damping rate, respectively. Please note that the primary objective of this study is to investigate the potential application of unidirectional electromagnetic modes in 3D EOT. In this investigation, we have deliberately chosen specific, yet well-established values for ωp, with an electron density of Ne = 1.1 × 1016 cm−3 and an effective mass ratio of m*/m0 = 0.014218. Additionally, we have set γ = 5 × 10−3ωp for all simulations. It’s worth noting that these parameters can be fine-tuned through methods such as doping22,23, temperature control24, and others.

The anisotropic permittivity tensor allows for breaking Lorentz reciprocity10, i.e., the equivalence of the forward and backward directions, thereby giving rise to unidirectional bands (k > 0 only, in a specific frequency region). Time-reversal symmetry is herein broken by the application of an external magnetic bias, of the order of 1 Tesla. Essentially, what this external magnetic field does is to induce a preferred direction in the helicoidal propagation of the electrons in InSb, thereby breaking the symmetry between “backward” and “forward” direction—i.e., giving rise to unidirectional (e.g., forward only) propagation. Then, depending on the choice of the upper cladding (Si, opaque material, InSb), one obtains the three distinct band-diagrams shown in Fig. 1 of the main paper, i.e., the upper layer allows ‘designing’ appropriately a specific band-diagram.

Fig. 1: Analysis of the band distribution in three distinct structures.
figure 1

Dispersion and schematic diagrams of the a Si-InSb structure with ωc = 0.25ωp (ωc is the electron cyclotron frequency and ωp is the plasma frequency), d1 = 0.08λp (λp = 2πc/ωp), and d2 = 0.12λp, b the opaque material (OM)-InSb structure with ωc = − 0.25ωp and d1 = d2 = 0.2λp, and c the InSb-InSb structure with ωc = 0.8ωp and d1 = d2 = 0.03λp. The dielectric constants used are εsi = 11.68 and ε∞ = 15.636,37. Red solid lines indicate the topological or robust nonreciprocal surface modes that can overcome nonlocal effects, while black dashed lines represent nonreciprocal modes propagating in only one direction but prone to nonlocal effects as they feature high wavenumbers. Black dotted lines in a and c represent the first-order resonance modes within the heterostructures with finite thicknesses. The edges of bulk-mode zones of an infinite InSb slab are denoted by blue dashed lines. The green-colored areas are the compressed bulk zone of the finite InSb layer. The inset of b shows the corresponding dispersion curves in the perfect electric conductor (PEC)-OM-InSb-PEC structure, and it is clear that there are two topological one-way curves in the topological area. The emerging topological one-way modes are sustained on the PEC-InSb interface18,32,38,39. a–c All InSb layers are assumed to be lossless (γ = 0) to clearly demonstrate the unaffected one-way bands40.

Full size image

In both structures (Si-InSb and OM-InSb), we observe a clear one-way band due to the breaking of time-reversal symmetry, as shown in Fig. 1a, b. In particular, the Si-InSb structure exhibits a one-way band, characteristic of asymptotic frequencies, while the OM-InSb structure features, first, a nonreciprocal asymptotic frequencies-based one-way band, and, second, a truly topological one-way band with the surface modes having finite wavenumbers (k), insulating them from nonlocal effects18. The OM-InSb configuration is surrounded by the perfect electric conductor (PEC, upper boundary) and the perfect magnetic conductor (PMC, lower boundary), which is required for preserving the one-way band. Indeed, the zoomed-in panel in Fig. 1b shows the dispersion curve had the lower boundary been PEC, revealing that the topological one-way band is closed. We emphasize here that even the PMC wall is not naturally occurring. Numerous research efforts have focused on achieving PMC properties by designing periodic resonant devices, such as the widely employed mushroom-engineered high-impedance surface (HIS)25 and graphene-based HIS26. Through careful engineering, these textured HIS structures can exhibit PMC behavior at specific resonant frequencies. It is essential to highlight that the width of these HIS structures is typically on the subwavelength scale (<λ0/10)25. According to our simulations, a PMC wall with a width of λ0/10 did not significantly affect the performance of 2D or 3D EOT. Therefore, it is plausible to consider textured HIS as a promising candidate for PMC boundaries in this work, which presents an intriguing avenue for future exploration beyond the scope of this paper. For our third considered structure, we note that the opaque material of the second structure is an idealized material, thus we replace it with unmagnetized InSb. From Fig. 1c (red solid line) we see that this replacement results in the opening of an upper one-way band supporting surface modes with finite wavenumber k, which are therefore expected to be robust against nonlocal effects. Specifically, our calculations show that the surface modes in that upper one-way band (yellow-colored area) have finite wavenumbers, with ∣k∣ < 10kp (kp = ωp/c). The importance of these diagrams is that they show that we can ‘cleanly’ excite single (topological or nonreciprocal) modes in the frequency regions of interest. Also, they show that some of these modes feature finite/small wavenumbers in the frequency regions of interest, as a result of which they are not prone to nonlocal effects.

Next, we rigorously analyze the impact of nonlocal effects in InSb-based structures. The hydrodynamic model is used to describe the nonlocality in InSb-based structures, which arises from the presence of spatial currents J18,20,27. The currents can be described by the following equation:

$${\beta }^{2}\nabla (\nabla \cdot {{{{{{{\bf{J}}}}}}}})+\omega (\omega +i\gamma ){{{{{{{\bf{J}}}}}}}}=i\omega \left({\omega }_{{{{{{{{\rm{p}}}}}}}}}^{2}{\varepsilon }_{0}{\varepsilon }_{\infty }{{{{{{{\bf{E}}}}}}}}+{{{{{{{\bf{J}}}}}}}}\times {\omega }_{{{{{{{{\rm{c}}}}}}}}}\hat{z}\right),$$
(2)

where β is the nonlocal parameter. In the limit of β = 0, Eq. (2) reduces to the classical Drude model, which implies that the current J at a point is determined solely by the electromagnetic field at that point. Since Maxwell’s equations require that J has the same wavenumber as the electric and magnetic fields, the nonlocal effect is expected to have little impact on electromagnetic waves with wavenumbers satisfying:

$$| k| \ll \omega /\beta$$
(3)

In this work, we assume a value of β = 1.07 × 106 m/s for n-type InSb28. For ω = ωp, Eq. (3) reduces to \(| \bar{k}| \ll c/\beta \approx 280\), where \(\bar{{{{{{{{\bf{k}}}}}}}}}={{{{{{{\bf{k}}}}}}}}/{{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{p}}}}}}}}}\). This indicates that the SMPs of interest in our third structure in Fig. 1 should be nearly immune to the nonlocal effect, regardless of the presence of SMPs with large k at higher frequencies (beyond the one-way band) near ωs (see Fig. 1c)—the resonance frequency of the bulk modes. To investigate the impact of the nonlocal effect on the propagation of SMPs in these structures, we analyze their properties using the numerical software COMSOL Multiphysics with a non-zero nonlocal parameter (β ≠ 0). To solve the partial differential equation (PDE), a weak-form relation is required. Therefore, we multiply Eq. (2) with a test current \(\tilde{{{{{{{{\bf{J}}}}}}}}}\), resulting in

$$\begin{array}{l}{\int}_{{{\Omega }}}\left[-{\beta }^{2}\nabla \cdot {{{{{{{\bf{J}}}}}}}}\nabla \cdot \tilde{{{{{{{{\bf{J}}}}}}}}}+\omega (\omega +i\gamma ){{{{{{{\bf{J}}}}}}}}\cdot \tilde{{{{{{{{\bf{J}}}}}}}}}\right.\\ \left.-i\omega \left({\epsilon }_{0}{\epsilon }_{\infty }{\omega }_{{{{{{{{\rm{p}}}}}}}}}^{2}{{{{{{{\bf{E}}}}}}}}+{{{{{{{\bf{J}}}}}}}}\times {\omega }_{{{{{{{{\rm{c}}}}}}}}}\hat{{{{{{{{\bf{z}}}}}}}}}\right)\cdot \tilde{{{{{{{{\bf{J}}}}}}}}}\right]d{{{{{{{\bf{r}}}}}}}}=0\end{array}$$
(4)

Figure 2 shows that, as expected, the magnetic-field distribution in the first Si-InSb structure exhibits significant spatial dispersion, resulting in backward modes within the nonreciprocal ‘one-way’ band. In the remaining structures, the SMPs maintain their unidirectional character, and the magnetic fields exhibit negligible differences between the local and nonlocal cases. As a result, we conclude that the Si-InSb structure is susceptible to realistic nonlocal effects because of the presence of a large wavenumber (k) in the one-way band (see Fig. 1a). By contrast, the OM/InSb-InSb structures sustain robust SMPs, having relatively small k values (k < 10kp) within their respective one-way bands, making them essentially immune to nonlocality.

Fig. 2: Demonstration of the impact of perturbing obstacles and/or nonlocal effects on the one-way surface magnetoplasmons (SMPs) in three structures.
figure 2

The magnetic-field distribution obtained from finite-element method (FEM) simulations of three different structures: a–c Si-InSb, d opaque material (OM)-InSb, and e InSb-InSb. The simulations were performed at different frequencies: a 0.68ωp (ωp is the plasma frequency), b 0.7ωp, c 0.8ωp, d 1.05ωp, and e 1.1ωp. The damping rate γ was set to 5 × 10−3ωp, and the nonlocal parameter β was set to 1.07 × 106 m/s. f Two-dimensional xy-plane magnetic-field distribution for each case shown (in 1D) in panels a–e, under nonlocal conditions (inside the blue rectangle). g Calculation of λeff of the SMPs in nonlocal cases by using FEM simulations. \({\lambda }_{{{{{{{{\rm{eff}}}}}}}}}^{-}\) and \({\lambda }_{{{{{{{{\rm{eff}}}}}}}}}^{+}\) are the effective wavelengths of backward and forward SMPs, respectively. neff ( = 2πc/(ωλeff), the effective index) and k ( = 2π/λeff, wavenumber) can be derived from λeff. γ = 0 and ω = 0.8ωp.

Full size image

Figure 2 directly demonstrates the proneness to nonlocal and perturbing effects of the Si-InSb structure and the corresponding robustness of the OM-InSb and InSb-InSb structures. In particular, Fig. 2a–c shows that, for the Si-InSb structure, as the operating frequency gradually increases from the lower asymptote to the upper one within the one-way band, the nonlocality-induced backward SMPs start exhibiting relatively large wavenumbers, making it difficult to couple with forward SMPs in the presence of defects or imperfections, and leading to rapid dissipation. For the subsequent section of this paper, we choose ω = 0.8ωp for the Si-InSb structure. We here note that the sources in all simulations were set as point dipoles to excite SMPs with arbitrarily large k in order to investigate the influence of nonlocal effects on SMPs in one-way bands. In practice, a real dipole in such a holey structure can only excite waves with k > 1/D (where D is the width of the dipole). Therefore, in theory, it is possible to selectively excite forward SMPs while avoiding the excitation of backward SMPs through careful design and selection of the excitation source. Compared to the Si-InSb structure, as seen in Fig. 2d, e and in the last two diagrams of Fig. 2f, the OM-InSb and InSb-InSb structures are immune to not only nonlocal effects but also to the presence of perturbing obstacles (air hole of radius r = 1 μm) directly inserted on their propagation direction. In essence, the Si-InSb and InSb-InSb structures belong to the nonreciprocal category, and both are subject to the influence of nonlocal effects. The faintly observable backward SMPs within the InSb-InSb structures arise due to the substantial gap between the lower boundary of the one-way band and the dispersion curves containing SMPs with k → − ∞. In such instances, the excited backward SMPs exhibit a substantial imaginary component of k or ω19, leading to their rapid absorption or attenuation. Thus, the robust nature of these two structures may clearly be asserted.

As our primary goal in this paper is not to achieve topological structures/modes, we demonstrate the impact of nonlocal effects on SMPs through simulations based on Eq. (4), as elaborated in Fig. 2. Additionally, dispersion curves for SMPs in nonlocal scenarios can be generated using the methodology proposed in ref. 18. It’s worth noting that finite-element method (FEM) simulations based on Eq. (4) can also be employed to calculate λeff, neff, and k by setting γ = 0 (lossless InSb). For instance, for the Si-InSb structure with ω = 0.8ωp, our lossless nonlocal simulations as shown in Fig. 2g yield λeff ≈ 1.9 μm, neff ≈ 98.7, and k ≈ 78.9kp. These results are consistent with those reported in ref. 18. Multiple commercial software, such as COMSOL Multiphysics, can be used to implement the FEM simulations in this paper.

The fact that the OM-InSb structure is “truly topological,” while the Si-InSb is not, has been established (for both of these structures) in previous work (ref. 18). A “truly topological” structure is immune to even nonlocal material effects, which appear for large wavevectors k18. The opposite is not necessarily true, i.e., a one-way (nonreciprocal) structure robust to nonlocal effects, such as the InSb-InSb one, is not necessarily topological.

Indeed, for the first structure (Si-InSb), the band Chern number is not an integer because the guide is not sufficiently well-behaved for an ‘infinite’ wavenumber18. By contrast, the OM-InSb structure does exhibit a topological one-way band in the high-frequency region because the gap Chern number for the upper bandgap is non-zero and equals +1, while the gap Chern number for the lower bandgap is –129,30,31. For the third structure (InSb-InSb), the red-colored band in Fig. 1 cuts the (pale-yellow-colored) one-way bandgap at a finite k > 0 value, i.e., k does not diverge. As a result, within that one-way bandgap, one can rigorously excite the forward-only surface magnetoplasmon (nonreciprocity), which will be immune to even nonlocal effects because k remains finite in this one-way bandgap—without necessarily the need for a topological character or topological protection.

In fact, in magneto-optical heterostructures, it is not always essential for the one-way mode to be topological or nonreciprocal, especially in practical applications. What is really needed is the existence of a one-way band, within which a surface mode can exist with finite wavevector k, so that nonlocal effects can be negligible.

Ultra-subwavelength 2D and 3D EOT

Similarly to classical surface plasmon polaritons, the presence of nonreciprocal or topological unidirectional SMPs in our structures allows for achieving EOT in two- or three-dimensional structures. Owing to their one-way propagation characteristics, SMPs on the Si/OM/InSb-InSb and air-InSb interfaces can couple with each other when a suitable hole/slit is opened at the rightmost end of the structure (see the upper part of Fig. 3). Physically, this efficient coupling (because of the absence of back-reflections) can further enhance the spatial squeezing and localization of SMPs around the hole, thereby dramatically improving their transmission through a slit (in 2D) or a hole (in 3D).

Fig. 3: Simulation results for two-dimensional (2D) and three-dimensional (3D) extraordinary optical transmission (EOT).
figure 3

Schematic diagrams and corresponding 2D simulations of three different structures with a 2 μm hole at the end: a Si-InSb (ω = 0.8ωp, λ0 = 187.5 μm), b opaque material (OM)-InSb (ω = 1.05ωp, λ0 ≈ 142.9 μm), and c InSb-InSb (ω = 1.1ωp, λ0 ≈ 136.4 μm). ωp is the plasma frequency and λ0 is the vacuum wavelength. Arrows in the simulations indicate the average power flow, which varies in direction based on the negative effective permittivity41,42,43. d Schematic diagram and finite-element method (FEM) simulations of 3D EOT, with all other parameters the same as in Fig. 1. The color bar for 2D simulations a–c is positioned between a and b, while the color bar for 3D simulations (d) is situated at d. e Definitions of the transmission efficiency (T), the incident energy ratio (IER), and the normalized T (Nt). The symbol “Pi” represents the energy transmitted through the waveguide or hole, with “i” indicating its location dependence.

Full size image

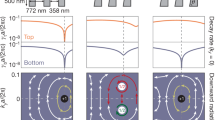
The upper panels in Fig. 3a–c illustrate the designed structures for achieving nonreciprocal/topological 2D EOT, while the lower respective panels display the corresponding electric-field distributions in the simulations, for a hole width of dhole = 2 μm. In the Si-InSb and InSb-InSb structures, the PEC wall was employed as the terminal, whereas in the OM-InSb structure, the PMC wall served as the terminal. In the case of Si-InSb and InSb-InSb structures, our simulations consistently show that the transmittance is typically lower when using the PMC terminal compared to the PEC terminal. This difference could be attributed to the stronger constraints imposed on the guided TM (Ex, Ey, Hz) waves in the PMC-terminated case, resulting in the maintenance of stronger localized energy around the hole. Conversely, it has been demonstrated that the OM-InSb structure exhibits higher transmittance when the PMC terminal is employed. This can be understood, as in the case of PEC termination, the guided wave can transfer to the SMPs sustained by the PEC-InSb interface (see the backward SMPs in the inset of Fig. 1b)18,32. Consequently, the OM-InSb structure was terminated using the PMC wall rather than the PEC wall, in accordance with the approach presented in ref. 18. Consistent with our previous work21, the Si-InSb structure exhibits relatively low transmission efficiency (T < 12%; see upper panels in Fig. 4). In contrast, the OM-InSb and InSb-InSb structures demonstrate significantly higher transmission efficiencies, with T ≈ 45% and T ≈ 65%, respectively. This difference in transmission efficiency can be attributed to the effective refractive indices of the structures, which are neff ≈ 5.7 (ω = 0.8ωp and k ≈ 4.56kp), neff ≈ 1.35 (ω = 1.05ωp and k ≈ 1.42kp), and neff ≈ 2.31 (ω = 1.1ωp and k ≈ 2.54kp) for the Si-InSb, OM-InSb, and InSb-InSb structures, respectively.

Fig. 4: The impact of hole position on extraordinary optical transmission (EOT).
figure 4

The transmission efficiency (T) and normalized T (Nt), as well as the incident energy ratio (IER), are plotted as functions of hole offset for the two-dimensional (2D) and three-dimensional (3D) EOT in a Si-InSb, b opaque material (OM)-InSb, and c InSb-InSb structures, where the hole width (dhole) is fixed at 2 μm. ωp, λ0, λeff, and Shole in the panels are the plasma frequency, the vacuum wavelength, the effective wavelength, and the hole area, respectively.

Full size image

We note that the overall effect explaining the enhanced (or not) transmission is a somewhat involved combination of impedance matching and losses. Generally, effective indices close to unity are beneficial in terms of transmission to the outside (air) region, since they imply better impedance matching and absence of reflection. However, this is here strictly true only when this is also accompanied by better localization of the guided mode in the lossless upper layer. For Fig. 3a, the guided mode has a high effective index (≈5.7) and, as we see, high localization in the lower, lossy, magnetized InSb layer—as a result, this combination leads to the smallest transmission, among the three cases, of <12%. For Fig. 3b, we note that the guided mode has a better value of effective index (≈1.35), but a significant part of the mode resides in the lower layer—resulting in T ≈ 45%—while for Fig. 3c we see that the guided mode has an effective index ≈ 2.31 and most of the mode is localized in the upper, lossless (unmagnetized) InSb, as a result of which the transmission via the small hole reaches T ≈ 65%—the highest among the three cases shown in Fig. 3.

To examine the presence or not of EOT, we also calculated the normalized transmission Nt (transmitted power divided by the power incident only on the slit or hole), and found \({{{N}_{t}^{{{{{{\rm{max}}}}}}}}}\approx 1.25\) (Si-InSb), \({{{N}_{t}^{{{{{{\rm{max}}}}}}}}}\approx 5\) (OM-InSb), and \({{{N}_{t}^{{{{{{\rm{max}}}}}}}}}\approx 18\) (InSb-InSb) (see Fig. 4, middle panels).

Next, we analyze the topological or nonreciprocal EOT in three-dimensional devices (Fig. 3d). In InSb-based one-way waveguides, the guiding modes are transverse-magnetic (TM) modes. Therefore, the presence of lateral PMC walls25,33,34 in the xy-plane will not destroy the topological property nor the EOT phenomenon. The thicknesses of the (three previous but now) 3D structures are h = 12 μm (0.064λ0, 0.36λeff), h = 5 μm (0.035λ0, 0.047λeff), and h = 4.5 μm (0.033λ0, 0.015λeff), respectively. We conducted 3D finite-element simulations of these deep-subwavelength structures and verified the presence of one-way propagation. For a hole with dhole = 2μm, and for a hole offset = − 0.5μm, we find 3D EOT with Nt ≈ 3 in the Si-InSb structure under the present conditions (see Fig. 4a, middle panel).

As it turns out, it is crucial to also study how the waveguide parameters, particularly the hole offset, affect the 2D and 3D topological/nonreciprocal EOT, as optimizing these parameters can lead to dramatically improved throughput performance. For the structures with dhole = 2 μm, the results of detailed simulations are presented in Fig. 4. Here, we introduce the incident energy ratio (IER) to characterize the energy distribution in the present magneto-optical structures. Specifically, IER is defined as the ratio of the incident energy over the hole region (Ehole) to the total incident energy (Etotal), such that IER = Ehole/Etotal. This parameter is used to emphasize the significance of the energy distribution in the structures. The value of Nt can then also be calculated using the following equation:

$${{{N}}}_{{{{{{{{\rm{t}}}}}}}}}={{T}}/{{{I}}}_{{{{{{{{\rm{ER}}}}}}}}}$$
(5)

Equation (5) can also be easily deduced through Fig. 3e. As shown in Fig. 3e, once P1 = P3, then T could be defined by P2/P5, IER is defined by P4/P5, and Nt is defined by P2/P4. Moreover, it is evident from Eq. (5) that EOT may occur in cases with low IER and/or high T. Our calculations, shown in Fig. 4a, for the 2D Si-InSb structure, reveal that most of the energy is concentrated in the Si layer, as the IER at a hole offset > 0 μm is typically larger than that in the region of hole offset < 0 μm. However, due to a lack of momentum matching, only a small part of the energy can successfully escape into the air. When the hole is located in the lower InSb layer, Nt can become greater than 1, with a maximum of 1.25—but for absolute T < 5%. Interestingly, for no hole offset the 3D structure actually outperforms its 2D counterpart. Specifically, as shown in Fig. 4a, we achieve Nt > 3 with T > 30%.

From Fig. 4b, we find that the energy in the opaque material layer of the 2D OM-InSb structure is higher than that in the InSb layer. Unlike the Si-InSb case, 2D EOT with Nt ≈ 5 can occur at a relatively high T (T ≈ 45%), while in the 3D case, it is Nt ≈ 3 (T ≈ 75%).

Remarkably, for the third (InSb-InSb) structure, we find extremely large EOT in both 2D and 3D cases (see Fig. 4c)—with the absolute (unnormalized) T for the 3D structure being ≈ 95% and Nt ≈ 40. The calculation of IER indicates that the energy distribution is similar to that in Fig. 4a, but here the attained transmission is substantially larger. Both, the 2D and 3D devices achieve EOT, with a maximum Nt ≈ 20 and Nt ≈ 40, respectively.

We also studied how the width of a hole, dhole, affects, both, the 2D and 3D topological/nonreciprocal EOT structures (see Fig. 5). Specifically, we now set dhole to 1 μm. For the Si-InSb structure, as shown in Fig. 5a, we observe that waves cannot easily out-couple to air in the 2D structure, resulting in a maximum T of less than 10%. However, for the 3D geometry, the maximum T is larger than 50%. We also find that the energy ratios IER are almost the same between the 2D and 3D structures. Thus, due to the relatively larger T in the 3D case, larger values of Nt are achieved in the 3D structure compared to the 2D one, with the maximum Nt reaching 4.88 for a hole offset ~ 0.25 μm.

Fig. 5: Effect of hole position on extraordinary optical transmission (EOT) with a smaller hole, compared to Fig. 4.
figure 5

The transmission efficiency (T) and normalized T (Nt), as well as the incident energy ratio (IER), are plotted as functions of hole offset for the two-dimensional (2D) and three-dimensional (3D) EOT in a Si-InSb, b opaque material (OM)-InSb, and c InSb-InSb structures, where the hole width (dhole) is fixed at 1 μm. λ0, λeff, and Shole in the panels are the vacuum wavelength, the effective wavelength, and the hole area, respectively.

Full size image

For the OM-InSb structure, as shown in Fig. 5b, the 2D and 3D EOT performances are not strongly affected by the change in dhole. The maximum values of T and Nt are nearly the same as with the previous (dhole = 2 μm, Fig. 4b) case. Specifically, we find that for the 2D case the maximum Nt is approximately 7, with T being approximately 50%, while for the 3D case Nt is approximately 3 and T is approximately 75%.

In the case of the InSb-InSb structure, as depicted in Fig. 5c, it is found that the maximum Nt reaches very large values: Approximately 41 for the 2D structure (for a T ≈ 49%), and approximately 17 for the 3D structure (for a T ≈ 36%). In other words, the robust nonreciprocal nature of this device (immune to nonlocal effects, as discussed above) and the absence of back-reflection(s), lead to excellent 3D EOT performance (through a single hole) even in the deep-subwavelength scale, where dhole < < λ0.

In addition, our proposed 3D one-way EOT structures, being inherently nonresonant, allow for broadband operation within each respective unidirectional band. To that end, Fig. 6 displays the calculated normalized transmissions for the aforementioned structures as the operating frequency varies within the one-way bands. We find that in the Si-InSb (refer to Fig. 6a) and OM-InSb (refer to Fig. 6b) structures, 3D EOT is achieved within a portion of the respective one-way bands, while 3D EOT is achieved throughout the entire one-way band in the InSb-InSb structure. We note that clear 3D EOT was observed in these structures, at different frequencies/bands, even when the hole position was kept unchanged for all cases. This represents a truly stringent condition given the complex relationship between the operating frequency, hole offset, hole size, and the maximum normalized transmission. Thus, by judicious choice of the structural (device) parameters, it is possible to achieve 3D one-way EOT throughout an entire (broadband) one-way band (cf. Fig. 6c).

Fig. 6: Analysis of the broadband extraordinary optical transmission (EOT) in three different structures.
figure 6

Broadband a nonreciprocal, b topological, and c nonreciprocal EOT in three dimensions. Normalized transmissions are shown for different operating frequencies within the corresponding one-way bands, for a the Si-InSb structure, b the opaque material (OM)-InSb structure, and c the InSb-InSb structure. dhole and ωp in the panels indicate the hole width and the plasma frequency, respectively.

Full size image

Moreover, it is noteworthy that while our work is based on simulation results, the 3D EOT phenomenon should be readily observable in experiments. Two challenges remain: (1) How can SMPs be efficiently excited? (2) How can a quasi-PMC be designed? For the first challenge, one potential approach is to engineer the structure and design grating configurations31,35 based on our proposed structures. Due to their subwavelength or ultra-subwavelength scale, the efficiency of excited SMPs should be considerable. Regarding the second challenge, as discussed earlier, the utilization and design of suitable HIS represent a promising avenue.

Conclusion

In summary, we have introduced and then studied in detail three different types of three-dimensional structures capable of attaining broadband, robust (nonreciprocal or topological) EOT through single holes: Si-InSb (nonreciprocal), OM-InSb (topological18,21), and InSb-InSb (robustly nonreciprocal, immune to nonlocal effects). The unidirectional surface waves sustained by the InSb-InSb device exhibit relatively small wavenumbers (k < 10kp), making them essentially immune to nonlocal effects. Because of the absence of back-reflections and the avoidance of the need for elongated tapering, our proposed structures exhibit nonreciprocal/topological 3D EOT with high absolute (T) and normalized (Nt) transmissions, even in the deep-subdiffraction regime. Specifically, for a hole surface of just \({{{{{{{{\rm{S}}}}}}}}}_{{{{{{{{\rm{hole}}}}}}}}}\approx 4.8\times 1{0}^{-4}{\lambda }_{0}^{2}\) (\(\approx 2.6\times 1{0}^{-3}{\lambda }_{{{{{{{{\rm{eff}}}}}}}}}^{2}\)), we found that the 3D InSb-InSb structure allows for near-perfect absolute transmission through the hole (T ≈ 95%, several orders of magnitude above existing near-field scanning optical microscopes of similar hole diameter8,16), and for normalized T far exceeding unity (Nt ≈ 40, EOT regime; see Fig. 4c). Our proposed 3D devices—immune to realistic device imperfections and nonlocal effects (cf. Fig. 2)—may form a platform for broadband, high-performance micro-/nano-scopy, heat-assisted magnetic recording, sensing, detection, enhancement of spontaneous emission and photoluminescence, and integrated photonic communication applications16 where there is a dire need for efficiently bringing light and electromagnetic waves to deep-subwavelength scales.

Methods

The simulated data used in this study have been generated using the finite-element method implemented in the software COMSOL Multiphysics.