Abstract
Multiplexed RNA sequencing in individual cells is transforming basic and clinical life sciences1,2,3,4. Often, however, tissues must first be dissociated, and crucial information about spatial relationships and communication between cells is thus lost. Existing approaches to reconstruct tissues assign spatial positions to each cell, independently of other cells, by using spatial patterns of expression of marker genes5,6—which often do not exist. Here we reconstruct spatial positions with little or no prior knowledge, by searching for spatial arrangements of sequenced cells in which nearby cells have transcriptional profiles that are often (but not always) more similar than cells that are farther apart. We formulate this task as a generalized optimal-transport problem for probabilistic embedding and derive an efficient iterative algorithm to solve it. We reconstruct the spatial expression of genes in mammalian liver and intestinal epithelium, fly and zebrafish embryos, sections from the mammalian cerebellum and whole kidney, and use the reconstructed tissues to identify genes that are spatially informative. Thus, we identify an organization principle for the spatial expression of genes in animal tissues, which can be exploited to infer meaningful probabilities of spatial position for individual cells. Our framework (‘novoSpaRc’) can incorporate prior spatial information and is compatible with any single-cell technology. Additional principles that underlie the cartography of gene expression can be tested using our approach.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The scRNA-seq datasets were acquired from the Gene Expression Omnibus (GEO) database with the following accession numbers: GSE99457 for the intestinal epithelium10, GSE84490 for the liver7, GSE95025 for the Drosophila embryo12, GSE66688 for the zebrafish embryo5 and GSE107585 for the kidney24. The cerebellum Slide-seq datasets23 were acquired from the Broad Institute Single Cell Portal (https://portals.broadinstitute.org/single_cell/study/slide-seq-study). The individual Drosophila embryos dataset22 is available as a supplementary information file of the original manuscript22. The BDTNP dataset was downloaded directly from the BDTNP webpage13.
Code availability
A Python package for novoSpaRc, and the scripts for reconstructing selected tissues presented in the manuscript, are provided at https://github.com/rajewsky-lab/novosparc.
References
Shapiro, E., Biezuner, T. & Linnarsson, S. Single-cell sequencing-based technologies will revolutionize whole-organism science. Nat. Rev. Genet. 14, 618–630 (2013).
Wagner, A., Regev, A. & Yosef, N. Revealing the vectors of cellular identity with single-cell genomics. Nat. Biotechnol. 34, 1145–1160 (2016).
Altschuler, S. J. & Wu, L. F. Cellular heterogeneity: do differences make a difference? Cell 141, 559–563 (2010).
Kolodziejczyk, A. A., Kim, J. K., Svensson, V., Marioni, J. C. & Teichmann, S. A. The technology and biology of single-cell RNA sequencing. Mol. Cell 58, 610–620 (2015).
Satija, R., Farrell, J. A., Gennert, D., Schier, A. F. & Regev, A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 33, 495–502 (2015).
Achim, K. et al. High-throughput spatial mapping of single-cell RNA-seq data to tissue of origin. Nat. Biotechnol. 33, 503–509 (2015).
Halpern, K. B. et al. Single-cell spatial reconstruction reveals global division of labour in the mammalian liver. Nature 542, 352–356 (2017).
Durruthy-Durruthy, R. et al. Reconstruction of the mouse otocyst and early neuroblast lineage at single-cell resolution. Cell 157, 964–978 (2014).
Waldhaus, J., Durruthy-Durruthy, R. & Heller, S. Quantitative high-resolution cellular map of the organ of Corti. Cell Rep. 11, 1385–1399 (2015).
Moor, A. E., et al., Spatial reconstruction of single enterocytes uncovers broad zonation along the intestinal villus axis. Cell 175, 1156–1167 (2018).
Habib, N. et al. Div-Seq: Single-nucleus RNA-seq reveals dynamics of rare adult newborn neurons. Science 353, 925–928 (2016).
Karaiskos, N. et al. The Drosophila embryo at single-cell transcriptome resolution. Science 358, 194–199 (2017).
Berkeley Drosophila Transcription Network Project. http://bdtnp.lbl.gov:8080/Fly-Net/.
Monge, G. Mémoire sur la théorie des déblais et des remblais. Historie de l’Academie Royale des Sciences de Paris 1781, 666–704 (1781).
Villani, C. Topics in Optimal Transportation (American Mathematical Society, 2003).
Villani, C. Optimal Transport: Old and New Vol. 338 (Springer, 2008).
Schiebinger, G. et al. Optimal-transport analysis of single-cell gene expression identifies developmental trajectories in reprogramming. Cell 176, 928–943 (2019).
Forrow, A. et al. Statistical optimal transport via geodesic hubs. Preprint at https://arxiv.org/abs/1806.07348 (2018).If ref. 18 (preprint) has now been published in final peer-reviewed form, please update the reference details if appropriate.
Mémoli, F., On the use of Gromov–Hausdorff distances for shape comparison. In Eurographics Symposium on Point-Based Graphics (eds Botsch, M. & Pajarola, R.) (Eurographics Association, 2007).
Peyré, G., Cuturi, M. & Solomon, J. Gromov–Wasserstein averaging of kernel and distance matrices. In Proc. 33rd International Conference on Machine Learning (Journal of Machine Learning Research, 2016).
Cuturi, M. Sinkhorn distances: lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems 26 (eds Burges, et al.) (NIPS, 2013).
Petkova, M. D., Tkačik, G., Bialek, W., Wieschaus, E. F. & Gregor, T. Optimal decoding of cellular identities in a genetic network. Cell 176, 844–855 (2019).
Rodriques, S. G. et al. Slide-seq: A scalable technology for measuring genome-wide expression at high spatial resolution. Science 363, 1463–1467 (2019).
Park, J. et al. Single-cell transcriptomics of the mouse kidney reveals potential cellular targets of kidney disease. Science 360, 758–763 (2018).
Eden, E., Navon, R., Steinfeld, I., Lipson, D. & Yakhini, Z. GOrilla: a tool for discovery and visualization of enriched GO terms in ranked gene lists. BMC Bioinformatics 10, 48 (2009).
Nüsslein-Volhard, C. & Wieschaus, E. Mutations affecting segment number and polarity in Drosophila. Nature 287, 795–801 (1980).
Rey, S. J. & Anselin, L. in Handbook of Applied Spatial Analysis (eds Fischer, M. & Getis, A.) 175–193 (Springer, 2010).
Tomancak, P. et al. Global analysis of patterns of gene expression during Drosophila embryogenesis. Genome Biol. 8, R145 (2007).
Acknowledgements
We thank A. Murray, A. Regev, T. Gregor, P. Rigollet, all members of our labs and many colleagues in the field for valuable comments and discussions. We thank L. Friedman for help with graphic design and illustration. This work was supported by the Israeli Science Foundation, through the I-CORE program (N.F.) and an Alexander von Humboldt Foundation Research Award (N.F.). N.K. was supported by grants DFG/GZ (Geschäftszeichen): RA 838/8-2 and DFG/GZ: KA 5006/1-1; and HGF Neurocure/GZ 0036-Phase 2-3. M.N. was supported by the James S. McDonnell Foundation, Schmidt Futures, the Israel Council for Higher Education and the John Harvard Distinguished Science Fellows Program within the FAS Division of Science of Harvard University. N.R. thanks Anna-Carina for useful discussions.
Author information
Authors and Affiliations
Contributions
N.R. conceived the structural correspondence assumption. N.K. and N.R. demonstrated the feasibility of such an assumption for spatial inference of toy models. M.N., N.K., N.F. and N.R. designed the research. M.N. developed the optimal-transport-based spatial inference framework. M.N. and N.K. implemented the method and performed computational and data analyses. N.F. and N.R. supervised the study. All authors wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Eileen Furlong and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Overview of probabilistic optimal matching using novoSpaRc and corresponding generative model.
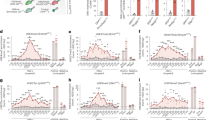
a, Based on the raw data of single cells in expression space and locations along a grid resembling the target tissue, graph structures are computed and distance matrices are derived from these graphs (Supplementary Methods). The two branches, and potentially a reference atlas, are aligned using novoSpaRc, under our structural correspondence assumption (distance in expression space on average monotonically increases with distance in physical space) and by using probabilistic embedding (Supplementary Methods). b, c, Left, visualization of noisy expression patterns for three random genes in models for 1-dimensional (1D) (b) and two-dimensional (2D) (c) tissues. Right, the original expression pattern for a representative gene, its coarse-grained representation (decreased spatial resolution) and its reconstruction using novoSpaRc. d, The Pearson correlation of the reconstructed expression pattern data to the original synthetic expression data increases with increasing signal-to-noise ratio, with the number of marker genes and with the fraction of informative genes, and exhibits non-monotonic behaviour with the α parameter. We note that α is an interpolation parameter (defined in the Methods section ‘Mathematical formulation of novoSpaRc’) between using only a reference atlas (α = 1) and using only structural information (driven by the structural correspondence assumption) (α = 1). Results are averaged over 100 instantiations of the generative model; data are mean ± s.d. The generative model and its default parameters are described in the Supplementary Methods.
Extended Data Fig. 2 Evaluation of novoSpaRc reconstruction of the intestinal epithelium and the liver lobule.
a, b, The fraction of cells in the crypt-to-villus axis (a) and the liver lobule axis (b) that is correctly assigned to its corresponding original villus zone10 and original lobule layer7, or is assigned to a zone up to d zones away from the original zone (x axis), is substantially higher than that of random assignment. c, d, novoSpaRc reconstructs the spatial expression patterns of the top zonated genes in the intestinal epithelium (c) (10 top zonated genes towards the crypt, and 10 top zonated genes towards V6) and in the liver lobule (d) (10 top zonated genes towards the central vein (CV), and 10 top zonated genes towards the portal node (PN)). 2810417H13Rik is also known as Pclaf. The selection of the top zonated genes is described in the Methods. The expression level of each gene in c and d is normalized to its maximum value.
Extended Data Fig. 3 novoSpaRc reconstruction of the intestinal epithelium and the liver lobule is robust and consistent with changing grid resolution.
a, b, Examples of FISH expression patterns of six zonated genes across the liver lobules, comparing the reconstructed (de novo vISH data) expression patterns produced by novoSpaRc to the expression patterns reported in a previous study7 (a), and the original (FISH) data (adapted from the same study7) (b). The visualization in a is a heat map, which shows the expression values of each gene across the lobule layers. The visualization of the reconstructed vISH data in b is intended to be comparable to the FISH images, and therefore the 1D reconstructed coordinates are projected onto a polar coordinate system (central vein–middle, portal node–outer circumference). c, The successful de novo reconstruction of the intestinal epithelium dataset9 is achieved for varying numbers of layers used for the target space (including both lower and higher numbers of layers compared with the original number (seven) of reference layers). The expression level of each gene is normalized to its maximum value.
Extended Data Fig. 4 novoSpaRc reconstruction of the Drosophila embryo on the basis of the BDTNP dataset is robust and self-consistent.
a, b, The Pearson correlation of the reconstructed expression patterns to the original FISH expression data12 increases with the number of genes used to construct the structural cellular graph in expression space (a), and with the fraction of those genes that are spatially informative (b). Spatially non-informative genes in this case were simulated as random Gaussian variables with mean and s.d. comparable to that of the original set of genes. c–f, The Pearson correlation of the reconstructed expression patterns to the original FISH expression data12 increases with the percentage of sampled single cells (without replacement) (c) and with the percentage of sampled single cells (with replacement) (d), and steadily decreases with noise level (e) and with the percentage of dropouts in the data (f). g, The mean value and variance of the optimization objective function (which we aim to minimize) increase with noise level. The results in a–g are averaged over 100 random choices of two marker genes; data are mean ± s.d. h, The Pearson correlation of the de novo reconstructed expression patterns to the original FISH data varies gradually with the entropic regularization parameter ε. i, The Pearson correlation of embedded de novo expression patterns of the BDTNP dataset12 for different values of the entropic regularization parameter ε with the expression pattern for ε = 5 × 10−5 (vertical dotted line). j, The spatial s.d. of embedded cells over the Drosophila embryo of the BDTNP dataset derived from de novo reconstruction by novoSpaRc is significantly lower than the s.d. derived from randomized embedding (P < 10−200, two-sided Kolmogorov–Smirnov test). Histograms show results for all 3,039 cells.
Extended Data Fig. 5 novoSpaRc accurately reconstructs the Drosophila embryo on the basis of the BDTNP dataset and single-cell data.
a, Examples of mapping probabilities of single cells produced by novoSpaRc for the Drosophila embryo, using the BDTNP dataset13. The predicted spatial positions of cells are distributed over relatively many locations when reconstruction is done de novo, and are more localized when marker genes are used. b, Histogram of Euclidean distances between the original cellular location of single cells and the most likely location predicted by novoSpaRc using one and two marker genes, compared to a histogram for random spatial predictions. c, The expression patterns of the two marker genes and one marker gene that were used for the results presented in a, b and in Fig. 3d, e. d, Visualization of reconstruction results for four transcription factors. The original FISH data are compared to reconstruction by novoSpaRc that exploits both structural and marker gene information (using two marker genes and one marker gene), and reconstruction without any marker gene information (de novo). Reconstruction that uses both structural and marker gene information (or a reference atlas) outperforms reconstruction that is based solely on a reference atlas. e, Visualization of novoSpaRc-based reconstruction results for the four transcription factors, based on single-cell data12 that exploit both structural and marker gene information (using 10–80 marker genes). The results in a–d are based on the BDTNP dataset13, and the results in e are based on a single-cell dataset12.
Extended Data Fig. 6 novoSpaRc identifies spatially informative archetypes by using scRNA-seq data for the Drosophila embryo.
The archetypes shown complement those of Fig. 4c, d. Preferred spatial positioning is denoted by colouring ranging from blue (low) to yellow (high). FISH images were taken from the BDGP database28. For genes for which an image was not available, DVEX12 was used instead. Two representative genes are shown for each spatial archetype. novoSpaRc accurately groups genes expressed in a particular domain—for example, the subdomain of the mesoderm, which is characterized by the transcription factor gcm (Archetype 5)—whereas it does not capture the details of the fine expression patterns of pair-rule genes (Archetype 8). CG42666 is also known as prage.
Extended Data Fig. 7 novoSpaRc reconstructs the zebrafish embryo.
a, Histograms assessing the increase in the accuracy of novoSpaRc reconstruction (measured by the Pearson correlation with FISH data5) with increasing number of marker genes. b, novoSpaRc reconstructs patterns of gene expression in the zebrafish embryo on the basis of only 15 marker genes, and the results improve as the number of marker genes increases. Top row, FISH data (reproduced from ref. 5); second row: Seurat predictions using 47 marker genes5; bottom three rows: novoSpaRc predictions using 15, 30 and 47 marker genes. The genes shown were not used in any of the reconstructions.
Extended Data Fig. 8 novoSpaRc reconstructs a whole-kidney dataset de novo.
a, Sketch of the major cell types that are reconstructed with novoSpaRc. b, Representative marker genes for each of the cell types shown in a. Top rows depict a rough positioning for each cell type in yellow–green; bottom rows show the gene expression predicted by novoSpaRc in the reconstructed tissue. Nphs1, podocytes; Nrp1, endothelial cells; Slc27a2, proximal tubule cells; Umod, loop of Henle; Pvalb, distal convoluted tubules; Aqp2, collecting duct cells. Expression ranges from low (blue) to high (yellow).
Extended Data Fig. 9 NovoSpaRc reconstructs single Drosophila embryos.
a, e, The averaged original expression of four gap genes (a) and four pair-rule genes (e) is shown for 101 and 177 individual Drosophila embryos, respectively22. Solid line, mean; dark shadow, s.d.; light shadow, minimum and maximum values over all embryos. b, f, Demonstration of the monotonic relationship between cellular pairwise distances in expression and physical space, consistent with the structural correspondence assumption. Data are mean ±s.d. c, g, The Pearson correlation increases with the number of marker genes used by novoSpaRc for the reconstruction of the remaining genes (α = 0.5) for both gap genes (c) and pair-rule genes (g). Using a reference atlas that corresponds to the individual embryo being reconstructed (‘individual atlas’) results in a consistently higher reconstruction quality than using an averaged reference atlas over all embryos (‘averaged atlas’). Data are mean ±s.d. d, h, Examples of the reconstruction of the expression patterns across a single random embryo, in which the reconstruction of each of the four genes is performed using the three complement genes as a reference, for both gap genes (d) and pair-rule genes (h). Note that the reconstructed expression patterns presented in d, h were computed while the corresponding gene in each case was not used for the reconstruction. The expression level of each gene in a, d, e, h is normalized to the maximum value over the mean expression of all embryos.
Extended Data Fig. 10 Comparison of spatial reconstruction with novoSpaRc versus available methods that fully rely on a reference atlas.
a, The Pearson correlation of the predicted versus the original spatial gene expression is shown as a function of the top 100 highly variable genes for the intestinal epithelium and liver datasets, or the number of marker genes used for the reconstruction for the BDTNP dataset, the Drosophila and zebrafish embryos and the brain cerebellum (84, 84, 45 and 745 genes, respectively). For the 1D datasets, the reconstructions are done de novo (with no reference atlas) and the existing baseline methods are inapplicable. For the liver, the last lobule layer was removed from the analysis, as only five cells were associated with it. For the 2D datasets, correlations are computed only for genes that were not used for the reconstructions. Note that for the Drosophila embryo novoSpaRc outperforms DistMap12, and for the zebrafish embryo novoSpaRc performs comparably to or better than Seurat5—although those methods were developed and tailored for the Drosophila and zebrafish embryos, respectively, and the best-performing threshold was chosen for DistMap. For the box plots, the centre line is the median, box limits are the 0.25 and 0.75 quantiles and whiskers extend to ±2.698 s.d. For the BDTNP dataset, the Drosophila and zebrafish embryos and the brain cerebellum, the results are shown for 100 random choices of marker genes. b, The intrinsic characteristics of novoSpaRc compared against Seurat5 and DistMap12.
Extended Data Fig. 11 Reconstruction quality varies with the α parameter.
Reconstructions of the BDTNP dataset, the Drosophila and zebrafish embryos and the brain cerebellum, with varying numbers of marker genes used for the reconstruction and different values of the α parameter. The reconstruction quality is quantified by calculating Pearson correlations between the predicted and the original patterns of gene expression for all genes that were not used as markers for the reconstruction. The quality of the reconstruction decreases for α = 1 in the BDTNP and brain cerebellum cases, which corresponds to reconstructing based only on reference marker genes, without taking the structural correspondence assumption into account. We note that α is an interpolation parameter (defined in the Methods section ‘Mathematical formulation of novoSpaRc’) between using only a reference atlas (α = 1) and using only structural information (driven by the structural correspondence assumption) (α = 1). For the box plots, the centre line is the median, box limits are the 0.25 and 0.75 quantiles and whiskers extend to ±2.698 s.d. Results are shown for 100 random choices of marker genes.
Supplementary information
Supplementary Information
This file contains Supplementary Methods, a Supplementary Discussion, Supplementary Tables 1-2 and Supplementary References.
Supplementary Data
This file contains 8 Supplementary Data files and a Supplementary Data guide.
Rights and permissions
About this article
Cite this article
Nitzan, M., Karaiskos, N., Friedman, N. et al. Gene expression cartography. Nature 576, 132–137 (2019). https://doi.org/10.1038/s41586-019-1773-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1773-3
This article is cited by
-
Multiscale biochemical mapping of the brain through deep-learning-enhanced high-throughput mass spectrometry
Nature Methods (2024)
-
TISSUE: uncertainty-calibrated prediction of single-cell spatial transcriptomics improves downstream analyses
Nature Methods (2024)
-
eSPRESSO: topological clustering of single-cell transcriptomics data to reveal informative genes for spatio–temporal architectures of cells
BMC Bioinformatics (2023)
-
SRTsim: spatial pattern preserving simulations for spatially resolved transcriptomics
Genome Biology (2023)
-
Spatial transcriptomics: recent developments and insights in respiratory research
Military Medical Research (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.