Abstract
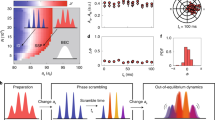
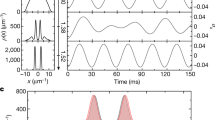
A supersolid is a counter-intuitive state of matter that combines the frictionless flow of a superfluid with the crystal-like periodic density modulation of a solid1,2. Since the first prediction3 in the 1950s, experimental efforts to realize this state have focused mainly on helium, in which supersolidity remains unobserved4. Recently, supersolidity has also been studied in ultracold quantum gases, and some of its defining properties have been induced in spin–orbit-coupled Bose–Einstein condensates (BECs)5,6 and BECs coupled to two crossed optical cavities7,8. However, no propagating phonon modes have been observed in either system. Recently, two of the three hallmark properties of a supersolid—periodic density modulation and simultaneous global phase coherence—have been observed in arrays of dipolar quantum droplets9,10,11, where the crystallization happens in a self-organized manner owing to intrinsic interactions. Here we directly observe the low-energy Goldstone mode, revealing the phase rigidity of the system and thus proving that these droplet arrays are truly supersolid. The dynamics of this mode is reminiscent of the effect of second sound in other superfluid systems12,13 and features an out-of-phase oscillation of the crystal array and the superfluid density. This mode exists only as a result of the phase rigidity of the experimentally realized state, and therefore confirms the superfluidity of the supersolid.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Leggett, A. J. Can a solid be “superfluid”? Phys. Rev. Lett. 25, 1543 (1970).
Boninsegni, M. & Prokof’ev, N. V. Colloquium: Supersolids: what and where are they? Rev. Mod. Phys. 84, 759 (2012).
Gross, E. P. Unified theory of interacting bosons. Phys. Rev. 106, 161 (1957).
Chan, M., Hallock, R. & Reatto, L. Overview on solid 4He and the issue of supersolidity. J. Low Temp. Phys. 172, 317–363 (2013).
Li, J. R. et al. A stripe phase with supersolid properties in spin-orbit-coupled Bose–Einstein condensates. Nature 543, 91–94 (2017).
Bersano, T. M. et al. Experimental realization of a long-lived striped Bose-Einstein condensate induced by momentum-space hopping. Phys. Rev. A 99, 051602 (2019).
Léonard, J., Morales, A., Zupancic, P., Donner, T. & Esslinger, T. Monitoring and manipulating Higgs and Goldstone modes in a supersolid quantum gas. Science 358, 1415–1418 (2017).
Léonard, J., Morales, A., Zupancic, P., Esslinger, T. & Donner, T. Supersolid formation in a quantum gas breaking a continuous translational symmetry. Nature 543, 87–90 (2017).
Böttcher, F. et al. Transient supersolid properties in an array of dipolar quantum droplets. Phys. Rev. X 9, 011051 (2019).
Tanzi, L. et al. Observation of a dipolar quantum gas with metastable supersolid properties. Phys. Rev. Lett. 122, 130405 (2019).
Chomaz, L. et al. Long-lived and transient supersolid behaviors in dipolar quantum gases. Phys. Rev. X 9, 021012 (2019).
Atkins, K. R. Liquid Helium (Cambridge Univ. Press, 1959).
Sidorenkov, L. A. et al. Second sound and the superfluid fraction in a Fermi gas with resonant interactions. Nature 498, 78 (2013).
Nambu, Y. & Jona-Lasinio, G. Dynamical model of elementary particles based on an analogy with superconductivity. Phys. Rev. 124, 246 (1961).
Griffin, A. et al. Excitations in a Bose-condensed Liquid Vol. 4 (Cambridge Univ. Press, 1993).
Anderson, P. W. Random-phase approximation in the theory of superconductivity. Phys. Rev. 112, 1900 (1958).
Goldstone, J. Field theories with superconductor solutions. Il Nuovo Cimento (1955–1965) 19, 154–164 (1961).
Higgs, P. W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 13, 508 (1964).
Yarnell, J., Arnold, G., Bendt, P. & Kerr, E. Energy vs momentum relation for the excitations in liquid helium. Phys. Rev. Lett. 1, 9 (1958).
Sooryakumar, R. & Klein, M. Raman scattering by superconducting-gap excitations and their coupling to charge-density waves. Phys. Rev. Lett. 45, 660 (1980).
Littlewood, P. & Varma, C. Gauge-invariant theory of the dynamical interaction of charge density waves and superconductivity. Phys. Rev. Lett. 47, 811 (1981).
Rüegg, C. et al. Quantum magnets under pressure: controlling elementary excitations in TlCuCl3. Phys. Rev. Lett. 100, 205701 (2008).
Stamper-Kurn, D. et al. Excitation of phonons in a Bose–Einstein condensate by light scattering. Phys. Rev. Lett. 83, 2876 (1999).
Bissbort, U. et al. Detecting the amplitude mode of strongly interacting lattice bosons by Bragg scattering. Phys. Rev. Lett. 106, 205303 (2011).
Endres, M. et al. The ‘Higgs’ amplitude mode at the two-dimensional superfluid/Mott insulator transition. Nature 487, 454–458 (2012).
Hoinka, S. et al. Goldstone mode and pair-breaking excitations in atomic Fermi superfluids. Nat. Phys. 13, 943–946 (2017).
Behrle, A. et al. Higgs mode in a strongly interacting fermionic superfluid. Nat. Phys. 14, 781–785 (2018).
Santos, L., Shlyapnikov, G. V. & Lewenstein, M. Roton-maxon spectrum and stability of trapped dipolar Bose–Einstein condensates. Phys. Rev. Lett. 90, 250403 (2003).
Chomaz, L. et al. Observation of roton mode population in a dipolar quantum gas. Nat. Phys. 14, 442–446 (2018).
Petter, D. et al. Probing the roton excitation spectrum of a stable dipolar Bose gas. Phys. Rev. Lett. 122, 183401 (2019).
Roccuzzo, S. M. & Ancilotto, F. Supersolid behavior of a dipolar Bose-Einstein condensate confined in a tube. Phys. Rev. A 99, 041601 (2019).
Wenzel, M., Böttcher, F., Langen, T., Ferrier-Barbut, I. & Pfau, T. Striped states in a many-body system of tilted dipoles. Phys. Rev. A 96, 053630 (2017).
Saccani, S., Moroni, S. & Boninsegni, M. Excitation spectrum of a supersolid. Phys. Rev. Lett. 108, 175301 (2012).
Macrì, T., Maucher, F., Cinti, F. & Pohl, T. Elementary excitations of ultracold soft-core bosons across the superfluid-supersolid phase transition. Phys. Rev. A 87, 061602 (2013).
Baillie, D. & Blakie, P. Droplet crystal ground states of a dipolar Bose gas. Phys. Rev. Lett. 121, 195301 (2018).
Tanzi, L. et al. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. Nature https://doi.org/10.1038/s41586-019-1568-6 (2019).
Natale, G. et al. Excitation spectrum of a trapped dipolar supersolid and its experimental evidence. Phys. Rev. Lett. 123, 050402 (2019).
Kadau, H. et al. Observing the Rosensweig instability of a quantum ferrofluid. Nature 530, 194–197 (2016).
Tang, Y., Sykes, A., Burdick, N. Q., Bohn, J. L. & Lev, B. L. s-wave scattering lengths of the strongly dipolar bosons 162Dy and 164Dy. Phys. Rev. A 92, 022703 (2015).
Tang, Y. et al. Anisotropic expansion of a thermal dipolar Bose gas. Phys. Rev. Lett. 117, 155301 (2016).
Tang, Y. et al. Thermalization near integrability in a dipolar quantum Newton’s cradle. Phys. Rev. X 8, 021030 (2018).
Baumann, K., Burdick, N. Q., Lu, M. & Lev, B. L. Observation of low-field Fano-Feshbach resonances in ultracold gases of dysprosium. Phys. Rev. A 89, 020701 (2014).
Böttcher, F. et al. Quantum correlations in dilute dipolar quantum droplets beyond the extended Gross-Pitaevskii equation. Preprint at https://arxiv.org/abs/1904.10349 (2019).
Ronen, S., Bortolotti, D. C. & Bohn, J. L. Bogoliubov modes of a dipolar condensate in a cylindrical trap. Phys. Rev. A 74, 013623 (2006).
Wilson, R. M., Ronen, S. & Bohn, J. L. Critical superfluid velocity in a trapped dipolar gas. Phys. Rev. Lett. 104, 094501 (2010).
Ferrier-Barbut, I., Kadau, H., Schmitt, M., Wenzel, M. & Pfau, T. Observation of quantum droplets in a strongly dipolar Bose gas. Phys. Rev. Lett. 116, 215301 (2016).
Ferrier-Barbut, I., Schmitt, M., Wenzel, M., Kadau, H. & Pfau, T. Liquid quantum droplets of ultracold magnetic atoms. J. Phys. B 49, 214004 (2016).
Ferrier-Barbut, I., Wenzel, M., Schmitt, M., Böttcher, F. & Pfau, T. Onset of a modulational instability in trapped dipolar Bose-Einstein condensates. Phys. Rev. A 97, 011604 (2018).
Brunello, A., Dalfovo, F., Pitaevskii, L., Stringari, S. & Zambelli, F. Momentum transferred to a trapped Bose-Einstein condensate by stimulated light scattering. Phys. Rev. A 64, 063614 (2001).
Blakie, P. B., Ballagh, R. J. & Gardiner, C. W. Theory of coherent Bragg spectroscopy of a trapped Bose-Einstein condensate. Phys. Rev. A 65, 033602 (2002).
Acknowledgements
We acknowledge discussions with the groups of F. Ferlaino, G. Modugno, L. Santos and T. Pohl, as well as with A. Pelster and A. Balaz. This work is supported by the German Research Foundation (DFG) within FOR2247 under Pf381/16-1 and Bu2247/1, Pf381/20-1 and FUGG INST41/1056-1. T.L. acknowledges support from the EU within Horizon2020 Marie Skłodowska Curie IF (grant numbers 746525 coolDips).
Author information
Authors and Affiliations
Contributions
M.G., F.B. and J.-N.S. performed the experiment and analysed the data. J.H. and M.W. performed the numerical analysis. H.P.B., T.L. and T.P. provided scientific guidance in experimental and theoretical questions. All authors contributed to the interpretation of the data and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Sean Mossman, Georgy Shlyapnikov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Theoretical phase boundaries.
As an indicator of the phase coherence, we show the ratio of the first minimum in the density compared to the central droplet peak density as an indicator of the overlap between the droplets43 of the calculated density profile of the ground state in red. The shaded area is the coherent region determined from the overlap. As in the experiment, three regions are identified and the coherent region locates between 94a0 and 97a0, shifting approximately 3a0 from the experimentally obtained phase diagram. These simulations are done for an atom number of 30 × 103. The black points indicate the measured average atom number in the experiment, with the error bars representing standard deviations for more than ten shots at each scattering length. (a.u., arbitrary units.).
Extended Data Fig. 2 Dynamic structure factor of the collective excitations.
Calculated structure factor S(ω, q) in the BEC phase for the scattering length as = 100a0 (a) and as = 98a0 (b) and in the supersolid droplet arrays (c) for as = 96a0. Owing to the finite size of the system, long-wavelength modes become discrete and the lowest possible excitation energy is set by the trap frequency (white horizontal line). For decreasing contact interaction strengths we can observe the roton minimum emerging, until finally its gap closes and the supersolid appears. In the supersolid regime we can clearly see the low-energy out-of-phase Goldstone mode and the large gap to all the other modes above the trap frequency of 30 Hz. The colour scale is normalized to the mode with the highest response across the scattering lengths shown.
Extended Data Fig. 3 Phase pattern of the Goldstone mode.
Shown are the density cut through the three-droplet ground state (black) along the x axis and the phase pattern (red) corresponding to the low-energy Goldstone mode.
Extended Data Fig. 4 Large-amplitude dynamics of the out-of-phase Goldstone mode.
Starting from an array of three droplets, the state can change to a four-droplet state for large excitation amplitudes. From there it either oscillates back and forth between the two (a) or the excitation amplitude is so large that we find that the motion is no longer oscillatory, with the excitation instead travelling only in one direction (b). Similar to Fig. 2, n(x) is the normalized line density along the x axis.
Extended Data Fig. 5 Simulated η–∆x correlation of the four-droplet dynamic states.
Numerically predicted correlation between the imbalance η and droplet displacement ∆x for the four-droplet states appearing at large excitation amplitudes of the low-energy Goldstone mode (blue points, with error bars indicating the uncertainty of the fit used to extract η and ∆x, as in Fig. 2). The red line is a linear fit.
Extended Data Fig. 6 Experimental correlation of the observed four-droplet states.
Similar to Fig. 3, we show the experimental correlation in the supersolid (97.6a0, a) and isolated droplet (91.2a0, b) regions, as well as example in situ images of four-droplet states, with n(x,y) the normalized density (c). For the four-droplet states we observe a clear correlation of imbalance and displacement throughout the supersolid region.
Extended Data Fig. 7 Variance of the four-droplet data with respect to the theoretical correlation.
Similar to Fig. 4b, we find that the variance of the four-droplet data with respect to the theoretical correlation curve (Extended Data Fig. 6) is lowest in the supersolid region. As in Fig. 4a, the shaded area is the coherent region determined experimentally. The error bars indicate one standard error of the experimental data with respect to the theoretical correlation.
Extended Data Fig. 8 Theory-independent evaluation.
Intersection point of the fit with the displacement axis for the three-droplet states (a) and the four-droplet states (b) obtained from a linear fit to the η–∆x correlation data across the part of the phase diagram we explored. An intersection point close to zero indicates the presence of a superfluid flow that can compensate fluctuations during the formation process. The error bars shown represent the standard error of the fitted intersections. As in Fig. 4a, the shaded area is the coherent region determined experimentally.
Rights and permissions
About this article
Cite this article
Guo, M., Böttcher, F., Hertkorn, J. et al. The low-energy Goldstone mode in a trapped dipolar supersolid. Nature 574, 386–389 (2019). https://doi.org/10.1038/s41586-019-1569-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1569-5
This article is cited by
-
Heating a dipolar quantum fluid into a solid
Nature Communications (2023)
-
Supersolidity in ultracold dipolar gases
Nature Reviews Physics (2023)
-
Apparatus for producing a \(^{168}\hbox {Er}\) Bose–Einstein condensate
Journal of the Korean Physical Society (2023)
-
Field-induced Bose-Einstein condensation and supersolid in the two-dimensional Kondo necklace
Communications Physics (2022)
-
Crystallization of bosonic quantum Hall states in a rotating quantum gas
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.