Abstract
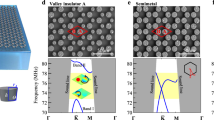
Guiding waves through a stable physical channel is essential for reliable information transport. However, energy transport in high-frequency mechanical systems, such as in signal-processing applications1, is particularly sensitive to defects and sharp turns because of back-scattering and losses2. Topological phenomena in condensed matter systems have shown immunity to defects and unidirectional energy propagation3. Topological mechanical metamaterials translate these properties into classical systems for efficient phononic energy transport. Acoustic and mechanical topological metamaterials have so far been realized only in large-scale systems, such as arrays of pendulums4, gyroscopic lattices5,6, structured plates7,8 and arrays of rods, cans and other structures acting as acoustic scatterers9,10,11,12. To fulfil their potential in device applications, mechanical topological systems need to be scaled to the on-chip level for high-frequency transport13,14,15. Here we report the experimental realization of topological nanoelectromechanical metamaterials, consisting of two-dimensional arrays of free-standing silicon nitride nanomembranes that operate at high frequencies (10–20 megahertz). We experimentally demonstrate the presence of edge states, and characterize their localization and Dirac-cone-like frequency dispersion. Our topological waveguides are also robust to waveguide distortions and pseudospin-dependent transport. The on-chip integrated acoustic components realized here could be used in unidirectional waveguides and compact delay lines for high-frequency signal-processing applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Olsson, R. H. III & El-Kady, I. Microfabricated phononic crystal devices and applications. Meas. Sci. Technol. 20, 012002 (2009).
Baboly, M. G. et al. Demonstration of acoustic waveguiding and tight bending in phononic crystals. Appl. Phys. Lett. 109, 183504 (2016).
Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).
Nash, L. M. et al. Topological mechanics of gyroscopic metamaterials. Proc. Natl Acad. Sci. USA 112, 14495–14500 (2015).
Mitchell, N. P., Nash, L. M., Hexner, D., Turner, A. M. & Irvine, W. T. M. Amorphous topological insulators constructed from random point sets. Nat. Phys. 14, 380–385 (2018).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342–345 (2018).
Yu, S. et al. Elastic pseudospin transport for integratable topological phononic circuits. Nat. Commun. 9, 3072 (2018).
He, C. et al. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 12, 1124–1129 (2016).
Lu, J. et al. Observation of topologically valley transport of sound in sonic crystals. Nat. Phys. 13, 369–374 (2017).
Yves, S., Fleury, R., Lemoult, F., Fink, M. & Lerosey, G. Topological acoustic polaritons: robust and sound manipulation at the subwavelength scale. New J. Phys. 19, 075003 (2017).
He, H. et al. Topological negative refraction of surface acoustic waves in a Weyl phononic crystal. Nature 560, 61–64 (2018).
Peano, V., Brendel, C., Schmidt, M. & Marquardt, F. Topological phases for sound and light. Phys. Rev. X 5, 031011 (2015).
Brendel, C., Peano, V., Painter, O. J. & Marquardt, F. Pseudomagnetic fields for sound at the nanoscale. Proc. Natl Acad. Sci. USA 114, E3390–E3395 (2017).
Brendel, C., Peano, V., Painter, O. J. & Marquardt, F. Snowflake phononic topological insulator at the nanoscale. Phys. Rev. B 97, 020102 (2018).
Huang, X. M. H., Zorman, C. A., Mehregany, M. & Roukes, M. L. Nanoelectromechanical systems: nanodevice motion at microwave frequencies. Nature 421, 496 (2003).
Craighead, H. G. Nanoelectromechanical systems. Science 290, 1532–1535 (2000).
De Alba, R. D. et al. Tunable phonon-cavity coupling in graphene membranes. Nat. Nanotechnol. 11, 741–746 (2016).
Faust, T., Rieger, J., Seitner, M. J., Kotthaus, J. P. & Weig, E. M. Coherent control of a classical nanomechanical two-level system. Nat. Phys. 9, 485–488 (2013).
Okamoto, H. et al. Coherent phonon manipulation in coupled mechanical resonators. Nat. Phys. 9, 485–488 (2013).
Hatanaka, D., Mahboob, I., Onomitsud, K. & Yamaguchi, H. Phonon waveguides for electromechanical circuits. Nat. Nanotechnol. 9, 520–524 (2014).
Hatanaka, D., Dodel, A., Mahboob, I., Onomitsud, K. & Yamaguchi, H. Phonon propagation dynamics in band-edngineered one-dimensional phononic crystal waveguides. New J. Phys. 17, 113032 (2015).
Cha, J. & Daraio, C. Electrical tuning of elastic wave propagation in nanomechanical lattices at MHz frequencies. Nat. Nanotechnol. 13, 1016–1020 (2018).
Kurosu, M., Hatanaka, D., Onomitsu, K. & Yamaguchi, H. On-chip temporal focusing of elastic waves in a phononic crystal waveguide. Nat. Commun. 9, 1331 (2018).
Wu, L. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).
Yves, S. et al. Crystalline metamaterials for topological properties at subwavelength scales. Nat. Commun. 8, 16023 (2017).
Bernevig, B. A., Hughes, T. L. & Zhang, S. C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Matlack, K. H., Serra-Garcia, M., Palermo, A., Huber, S. D. & Daraio, C. Designing perturbative metamaterials from discrete models. Nat. Mater. 17, 323–328 (2018).
Chen, C. et al. Graphene mechanical oscillators with tunable frequency. Nat. Nanotechnol. 8, 923–927 (2013).
Bagci, T. et al. Optical detection of radio waves through a nanomechanical transducer. Nature 507, 81–85 (2014).
Cheng, X. et al. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 15, 542–548 (2016).
Acknowledgements
J.C. and C.D. acknowledge partial support for this project from NSF EFRI award number 1741565, and the Kavli Nanoscience Institute at Caltech. K.W.K. acknowledges support for this project from the “Overseas Research Program for Young Scientists” programme through the Korea Institute for Advanced Study (KIAS).
Reviewer information
Nature thanks S. Iwamoto and the other anonymous reviewers for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
J.C. and C.D. conceived the idea of the research. J.C. designed and fabricated the samples, built the experimental setups and performed the measurements. J.C. also performed all numerical simulations. J.C. and K.W.K. performed the theoretical studies. J.C., K.W.K. and C.D. analysed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Fabrication.
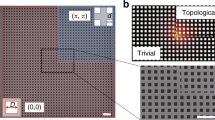
a, Etch holes are periodically arranged in an extended honeycomb lattice. a is a lattice parameter and w is the distance between two neighbouring etch holes. The bottom picture shows the cross-sectional view. b, After a sample is immersed in a buffered oxide etchant, the thermal SiO2 is radially etched from the etch holes. The etching paths are illustrated by the brown circles with radius r. The overlap between two membranes affects the coupling strength, by controlling the distance w. c, Optical microscope image of a partially etched samples. The yellow circles represent free-standing SiNx membranes and the darker/purple region is SiNx/SiO2. Scale bar, 18 μm.
Extended Data Fig. 2 Unit cell structures for the different topological phases.
a–c, Unit cell geometries for w = 5.5 μm (a), w = 6.0 μm (b) and w = 6.5 μm (c). Here, r = 4.9 μm is the etching distance from the centre of the etch holes. The central hexagon and the six corners represent the regions of unetched thermal SiO2. These are modelled as fixed boundaries in finite element simulations.
Extended Data Fig. 3 Experimental characterization of the straight topological edge waveguide.
a, Frequency responses (amplitude only) obtained from a spatial scan of 20 sites of the straight edge waveguide. The scanning period is 18 μm. The intensity decay around 15 MHz represents a defect mode. b, Amplitude × sin(phase) responses obtained from the spatial scan. c, Frequency dispersion obtained from Fourier transformation of the data shown in b.
Extended Data Fig. 4 Characteristics of the defect mode.
a, Optical microscope image of the excitation region and the defective unit including the gold electrode. b, Experimental data for the amplitude decay of the defect mode. The red squares denote the experimental data and the black solid line represents a fitting function. Here, the fitting parameters a and b are 1.408 mV and 114.1292 μm.
Extended Data Fig. 5 Characteristics of the distorted waveguide.
a, Frequency dispersion curve along the edge waveguide. b, Frequency responses of the bulk of the non-trivial phase (left), the output of the edge waveguide (middle), and the bulk of the trivial phase (right). c, A spatiotemporal response of unfiltered propagating pulses with broadband frequencies ranging from 12.8 MHz to 15.8 MHz. d–k, Filtered spatiotemporal responses of the propagating pulses with different centre frequencies. The bandwidth of the pulses is 0.3 MHz. The centre frequencies are 13.48 MHz (d), 13.68 MHz (e), 13.85 MHz (f), 14.1 MHz (g), 14.35 MHz (h), 14.75 MHz (i), 14. 975 MHz (j) and 15.23 MHz (k).
Extended Data Fig. 6 Frequency responses of the NEMM with the pseudospin filter configuration.
a–e, Frequency responses of the bulk of the non-trivial phase (w = 6.5 μm; a), output 1 (b), output 2 (c), output 3 (d) and the bulk of the trivial phase (w = 5.5 μm; e), shown in Fig. 4a. The light-red and light-blue regions represent the bandgaps of the non-trivial and trivial phases, respectively.
Supplementary information
Video 1: Time evolution of the plate vibrational mode at point 1 in Figure 2f.
The corresponding wavenumber and eigenfrequency are 17,453 m−1 and 14.77 MHz.
Video 2: Time evolution of the plate vibrational mode at point 2 in Figure 2f.
The corresponding wavenumber and eigenfrequency are -17,453 m−1 and 15.15 MHz.
Video 3: Time evolution of the plate vibrational mode at point 3 in Figure 2f.
The corresponding wavenumber and eigenfrequency are -17,453 m−1 and 14.77 MHz.
Video 4: Time evolution of the plate vibrational mode at point 4 in Figure 2f.
The corresponding wavenumber and eigenfrequency are 17,453 m−1 and 15.15 MHz.
Rights and permissions
About this article
Cite this article
Cha, J., Kim, K.W. & Daraio, C. Experimental realization of on-chip topological nanoelectromechanical metamaterials. Nature 564, 229–233 (2018). https://doi.org/10.1038/s41586-018-0764-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0764-0
Keywords
This article is cited by
-
Robust boundary-induced bulk propagations in elastic waveguides with nonplanar surfaces
Science China Physics, Mechanics & Astronomy (2024)
-
General duality and magnet-free passive phononic Chern insulators
Nature Communications (2023)
-
Selectable diffusion direction with topologically protected edge modes
Communications Physics (2023)
-
Topological materials for elastic wave in continuum
Acta Mechanica Sinica (2023)
-
A study on vibration localization and energy harvesting of periodic acoustic black hole structure
Meccanica (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.