Abstract
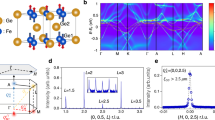
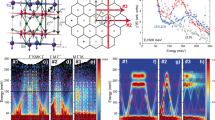
Owing to the unusual geometry of kagome lattices—lattices made of corner-sharing triangles—their electrons are useful for studying the physics of frustrated, correlated and topological quantum electronic states1,2,3,4,5,6,7,8,9. In the presence of strong spin–orbit coupling, the magnetic and electronic structures of kagome lattices are further entangled, which can lead to hitherto unknown spin–orbit phenomena. Here we use a combination of vector-magnetic-field capability and scanning tunnelling microscopy to elucidate the spin–orbit nature of the kagome ferromagnet Fe3Sn2 and explore the associated exotic correlated phenomena. We discover that a many-body electronic state from the kagome lattice couples strongly to the vector field with three-dimensional anisotropy, exhibiting a magnetization-driven giant nematic (two-fold-symmetric) energy shift. Probing the fermionic quasi-particle interference reveals consistent spontaneous nematicity—a clear indication of electron correlation—and vector magnetization is capable of altering this state, thus controlling the many-body electronic symmetry. These spin-driven giant electronic responses go well beyond Zeeman physics and point to the realization of an underlying correlated magnetic topological phase. The tunability of this kagome magnet reveals a strong interplay between an externally applied field, electronic excitations and nematicity, providing new ways of controlling spin–orbit properties and exploring emergent phenomena in topological or quantum materials10,11,12.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Mekata, M. Kagome: the story of the basketweave lattice. Phys. Today 56, 12 (2003).
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).
Ohgushi, K., Murakami, S. & Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: chiral spin state based on a ferromagnet. Phys. Rev. B 62, R6065 (2000).
Yan, S., Huse, D. A. & White, S. R. Spin-liquid ground state of the S=1/2 kagome Heisenberg antiferromagnet. Science 332, 1173–1176 (2011).
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012).
Mazin, I. I. et al. Theoretical prediction of a strongly correlated Dirac metal. Nat. Commun. 5, 4261 (2014).
Chisnell, R. et al. Topological magnon bands in a kagome lattice ferromagnet. Phys. Rev. Lett. 115, 147201 (2015).
Xu, G., Lian, B. & Zhang, S.-C. Intrinsic quantum anomalous Hall effect in the kagome lattice Cs2LiMn3F12. Phys. Rev. Lett. 115, 186802 (2015).
Zhu, W., Gong, S.-S., Zeng, T.-S., Fu, L. & Sheng, D. S. Interaction-driven spontaneous quantum Hall effect on a kagome lattice. Phys. Rev. Lett. 117, 096402 (2016).
Soumyanarayanan, A., Reyren, N., Fert, A. & Panagopoulos, C. Emergent phenomena induced by spin–orbit coupling at surfaces and interfaces. Nature 539, 509–517 (2016).
Keimer, B. & Moore, J. E. The physics of quantum materials. Nat. Phys. 13, 1045–1055 (2017).
Tokura, Y., Kawasaki, M. & Nagaosa, N. Emergent functions of quantum materials. Nat. Phys. 13, 1056–1068 (2017).
Kida, T. et al. The giant anomalous Hall effect in the ferromagnet Fe3Sn2 – a frustrated kagome metal. J. Phys. Condens. Matter 23, 112205 (2011).
Wang, Q., Sun, S., Zhang, X., Pang, F. & Lei, H. Anomalous Hall effect in a ferromagnetic Fe3Sn2 single crystal with a geometrically frustrated Fe bilayer kagome lattice. Phys. Rev. B 94, 075135 (2016).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015).
Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2, e1501870 (2016).
Kuroda, K. et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090–1095 (2017).
Ye, L. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018).
Fenner, L. A., Dee, A. A. & Wills, A. S. Non-collinearity and spin frustration in the itinerant kagome ferromagnet Fe3Sn2. J. Phys. Condens. Matter 21, 452202 (2009).
Hou, Z. et al. Observation of various and spontaneous magnetic skyrmionic bubbles at room temperature in a frustrated kagome magnet with uniaxial magnetic anisotropy. Adv. Mater. 29, 1701144 (2017).
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic Fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 153–178 (2010).
Borzi, R. A. et al. Formation of a nematic fluid at high fields in Sr3Ru2O7. Science 315, 214–217 (2007).
Chuang, T. M. et al. Nematic electronic structure in the “parent” state of the iron-based superconductor Ca(Fe1-xCox)2As2. Science 327, 181–184 (2010).
Fujita, K. et al. Simultaneous transitions in cuprate momentum-space topology and electronic symmetry breaking. Science 344, 612–616 (2014).
Bode, M. et al. Magnetization-direction-dependent local electronic structure probed by scanning tunneling spectroscopy. Phys. Rev. Lett. 89, 237205 (2002).
Hanneken, C. et al. Electrical detection of magnetic skyrmions by tunnelling non-collinear magnetoresistance. Nat. Nanotechnol. 10, 1039–1042 (2015).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Guo, H. M. & Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 80, 113102 (2009).
Nishimoto, S. et al. Metal-insulator transition of fermions on a kagome lattice at 1/3 filling. Phys. Rev. Lett. 104, 196401 (2010).
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 73, 233–235 (1990).
Seki, S. & Mochizuki, M. Skyrmions in Magnetic Materials 22–26 (Springer, Cham, 2016)
Montoya, S. A. et al. Tailoring magnetic energies to form dipole skyrmions and skyrmion lattices. Phys. Rev. B 95, 024415 (2017).
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed matter realization of the “parity anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988).
Hasan, M. Z. et al. topological insulators, helical topological superconductors and Weyl fermion semimetals. Phys. Scr. T164, 014001 (2015); corrigendum T168, 019501 (2016).
Xu, S. Y. et al. Hedgehog spin texture and Berry’s phase tuning in a magnetic topological insulator. Nat. Phys. 8, 616–622 (2012).
Acknowledgements
Experimental and theoretical work at Princeton University was supported by the Gordon and Betty Moore Foundation (GBMF4547/Hasan) and the United States Department of Energy (US DOE) under the Basic Energy Sciences programme (grant number DOE/BES DE-FG-02-05ER46200). Work at the Institute of Physics of the Chinese Academy of Science (IOP CAS) was supported by the National Key R&D Program of China (grant number 2017YFA0206303). Work at Boston College is supported by US DOE grant DE-FG02-99ER45747. We also acknowledge the Natural Science Foundation of China (grant numbers 11790313, 11774422 and 11774424), National Key R&D Program of China (numbers 2016YFA0300403 and 2017YFA0302903), the Key Research Program of the Chinese Academy of Sciences (number XDPB08-1), Princeton Center for Theoretical Science (PCTS) and Princeton Institute for the Science and Technology of Materials (PRISM)’s Imaging and Analysis Center at Princeton University. T.-R.C. was supported by the Ministry of Science and Technology under a MOST Young Scholar Fellowship (MOST Grant for the Columbus Program number 107-2636-M-006-004-), the National Cheng Kung University, Taiwan, and the National Center for Theoretical Sciences (NCTS), Taiwan. M.Z.H. acknowledges support from Lawrence Berkeley National Laboratory and the Miller Institute of Basic Research in Science at the University of California, Berkeley in the form of a Visiting Miller Professorship. We thank D. Huse and T. Neupert for discussions.
Reviewer information
Nature thanks S. Sachdev and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
J.-X.Y. and S.S.Z. conducted the STM and STS experiments in consultation with M.Z.H.; H.L.,W.W., C.X. and S.J. synthesized and characterized the sequence of samples; K.J., G.C., B.Z., B.L., K.L., T-R.C., H.L., Z.-Y.L. and Z.W. carried out theoretical analysis in consultation with J.Y. and M.Z.H.; I.B., T.A.C., H.Z., S.-Y.X. and G.B. contributed to sample characterization and instrument calibration; J.-X.Y., S.S.Z. and M.Z.H performed the data analysis and figure development and wrote the paper with contributions from all authors; M.Z.H. supervised the project. All authors discussed the results, interpretation and conclusion.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Longitudinal resistivity measurement.
The longitudinal resistivity ρxx was measured from 380 K to 5 K at zero magnetic field. The current was applied along the a–b plane.
Extended Data Fig. 2 Magnetization at 5 K in different magnetic field directions.
The sharp saturation of the magnetization curve for the in-plane field suggests that the easy magnetization axis lies in the a–b plane.
Extended Data Fig. 3 Interlayer resistivity evolution as a function of in-plane field azimuth angle.
The black line is the fitting curve. The inset shows a schematic of the sample (black hexagon) with the concentric electrical contacts used in such measurements (inner blue circle, voltage contacts; outer blue ring, current contacts).
Extended Data Fig. 4 Spectroscopic maps with vector-field conditions.
a, Topography of a large FeSn surface. b, Differential conductance map taken in the area shown in a at the energy of the side peak. c, Differential conductance maps with various vector-field conditions taken in the area shown in a at the energy of the side peak. The black arrow indicates the a axis and the red arrow represents the field vector. Their corresponding FFT images (known as QPI signals) are shown in Fig. 3.
Extended Data Fig. 5 Topographic image of a FeSn surface, showing two kinds of dark-spot defect.
The centres of the defects are located at Fe and Sn sites, based on the atomic assignment from Fig. 1.
Extended Data Fig. 6 Nonmagnetic scattering channels for helical spin–momentum texture with different magnetization directions.
a, The upper panel shows that spins cant towards the c axis to generate a net c-axis magnetization. The lower panel shows that backscattering is allowed in all directions. b, c, To generate a net in-plane magnetization, the momentum of the band shifts perpendicular to the in-plane direction and the spins reorganize their directions (similar to the Edelstein effect31), as shown in the upper panels (the faded red arrows represent helical spin texture without magnetization for reference). The spins are still locked perpendicular to the original momentum centre31 (black circle). The lower panels show that backscattering is allowed only in the magnetization direction and forbidden in the perpendicular direction owing to spin reversal.
Extended Data Fig. 7 Lorentz transmission electron microscopy images of the magnetic domain structures taken at different temperatures after turning off the external 0.7-T magnetic field applied along the c axis.
The measurement is taken in the a–b plane in these images and the different shades indicate the different orientation of the spin relative to the a–b plane. The skyrmions and stripe domains gradually disappear when the temperature drops to 130 K.
Extended Data Fig. 8 STM results on Mn3Sn.
a, b, Single crystals of Mn3Sn and Fe3Sn2, respectively. c, d, Typical STM images of the cleavage surface of Mn3Sn showing no clear atomic lattice structure.
Extended Data Fig. 9 Kagome lattice model.
a, Kagome lattice with Kane–Mele SOI. Here, \({v}_{{\rm{A}}{\rm{B}}}=2({{\boldsymbol{d}}}_{1}\times {{\boldsymbol{d}}}_{2})\cdot {\boldsymbol{z}}/\sqrt{3}=-1\), where d1 is the unit vector from A to C and d2 is the unit vector from C to B. b, Flux Ω enclosed by the fundamental plaquette formed by sites A, B and C on the kagome lattice.
Extended Data Fig. 10 Band dispersion from the kagome model.
a, Red lines are the band structure for Mi along the z direction (Mc) with a Dirac mass generated by λ. Blue lines are the band structure for Mi in the x–y plane (Mab), showing a vanishing Dirac mass gap even in the presence of λ. b, Similar to a but including bilayer splitting due to interlayer coupling. Only the spin minority bands are shown.
Extended Data Fig. 11 Effect of spin Berry phase.
a, The spin Berry phase Ωijk is equal to half the solid angle formed by spins Si, Sj and Sk. b, An electron hopping in the chiral spin background is equivalent to hopping in the presence of a gauge flux Ω. c, Band structures in the presence of both λand chiral flux Ω, when the magnetic field and the magnetization are along the x–y plane (Mab) and the z direction (Mc).
Rights and permissions
About this article
Cite this article
Yin, JX., Zhang, S.S., Li, H. et al. Giant and anisotropic many-body spin–orbit tunability in a strongly correlated kagome magnet. Nature 562, 91–95 (2018). https://doi.org/10.1038/s41586-018-0502-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0502-7
Keywords
This article is cited by
-
Sub-cycle multidimensional spectroscopy of strongly correlated materials
Nature Photonics (2024)
-
Distinct switching of chiral transport in the kagome metals KV3Sb5 and CsV3Sb5
npj Quantum Materials (2024)
-
Correlated order at the tipping point in the kagome metal CsV3Sb5
Nature Physics (2024)
-
Spin Berry curvature-enhanced orbital Zeeman effect in a kagome metal
Nature Physics (2024)
-
Anomalous electrons in a metallic kagome ferromagnet
Nature (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.