Abstract
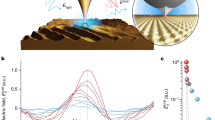
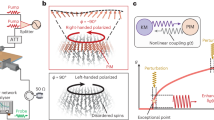
Creating optical components that allow light to propagate in only one direction—that is, that allow non-reciprocal propagation or ‘isolation’ of light—is important for a range of applications. Non-reciprocal propagation of sound can be achieved simply by using mechanical components that spin1,2. Spinning also affects de Broglie waves3, so a similar idea could be applied in optics. However, the extreme rotation rates that would be required, owing to light travelling much faster than sound, lead to unwanted wobbling. This wobbling makes it difficult to maintain the separation between the spinning devices and the couplers to within tolerance ranges of several nanometres, which is essential for critical coupling4,5. Consequently, previous applications of optical6,7,8,9,10,11,12,13,14,15,16,17 and optomechanical10,17,18,19,20 isolation have used alternative methods. In hard-drive technology, the magnetic read heads of a hard-disk drive fly aerodynamically above the rapidly rotating disk with nanometre precision, separated by a thin film of air with near-zero drag that acts as a lubrication layer21. Inspired by this, here we report the fabrication of photonic couplers (tapered fibres that couple light into the resonators) that similarly fly above spherical resonators with a separation of only a few nanometres. The resonators spin fast enough to split their counter-circulating optical modes, making the fibre coupler transparent from one side while simultaneously opaque from the other—that is, generating irreversible transmission. Our setup provides 99.6 per cent isolation of light in standard telecommunication fibres, of the type used for fibre-based quantum interconnects22. Unlike flat geometries, such as between a magnetic head and spinning disk, the saddle-like, convex geometry of the fibre and sphere in our setup makes it relatively easy to bring the two closer together, which could enable surface-science studies at nanometre-scale separations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R. & Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014).
Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).
Hasselbach, F. & Nicklaus, M. Sagnac experiment with electrons: observation of the rotational phase shift of electron waves in vacuum. Phys. Rev. A 48, 143–151 (1993).
Dubreuil, N. et al. Eroded monomode optical fiber for whispering-gallery mode excitation in fused-silica microspheres. Opt. Lett. 20, 813–815 (1995).
Spillane, S. M., Kippenberg, T. J., Painter, O. J. & Vahala, K. J. Ideality in a fiber-taper-coupled microresonator system for application to cavity quantum electrodynamics. Phys. Rev. Lett. 91, 043902 (2003).
Chang, L. et al. Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat. Photon. 8, 524–529 (2014).
Gallo, K., Assanto, G., Parameswaran, K. R. & Fejer, M. M. All-optical diode in a periodically poled lithium niobate waveguide. Appl. Phys. Lett. 79, 314–316 (2001).
Ibrahim, S. K., Bhandare, S., Sandel, D., Zhang, H. & Noe, R. Non-magnetic 30 dB integrated optical isolator in III/V material. Electron. Lett. 40, 1293–1294 (2004).
Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photon. 3, 91–94 (2009); corrigendum 3, 303 (2009).
Kang, M. S., Butsch, A. & Russell, P. S. J. Reconfigurable light-driven opto-acoustic isolators in photonic crystal fibre. Nat. Photon. 5, 549–553 (2011).
Lira, H., Yu, Z., Fan, S. & Lipson, M. Electrically driven nonreciprocity induced by interband photonic transition on a silicon chip. Phys. Rev. Lett. 109, 033901 (2012).
Fan, L. et al. An all-silicon passive optical diode. Science 335, 447–450 (2012).
Poulton, C. G. et al. Design for broadband on-chip isolator using stimulated Brillouin scattering in dispersion-engineered chalcogenide waveguides. Opt. Express 20, 21235–21246 (2012).
Hafezi, M. & Rabl, P. Optomechanically induced non-reciprocity in microring resonators. Opt. Express 20, 7672–7684 (2012).
Peng, B. et al. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 10, 394–398 (2014).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Shen, Z. et al. Experimental realization of optomechanically induced non-reciprocity. Nat. Photon. 10, 657–661 (2016).
Kim, J., Kim, S. & Bahl, G. Complete linear optical isolation at the microscale with ultralow loss. Sci. Rep. 7, 1647 (2017).
Fang, K. et al. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 13, 465–471 (2017).
Ruesink, F., Miri, M.-A., Alù, A. & Verhagen, E. Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat. Commun. 7, 13662 (2016).
Gross, W. A. Gas Film Lubrication (Wiley, New York, 1962).
Shomroni, I., Rosenblum, S., Lovsky, Y. & Bechler, O. All-optical routing of single photons by a one-atom switch controlled by a single photon. Science 345, 903–906 (2014).
Franke-Arnold, S., Gibson, G., Boyd, R. W. & Padgett, M. J. Rotary photon drag enhanced by a slow-light medium. Science 333, 65–67 (2011).
Matthewson, M., Kurkjian, C. R. & Gulati, S. T. Strength measurement of optical fibers by bending. J. Am. Ceram. Soc. 69, 815–821 (1986).
Malykin, G. B. The Sagnac effect: correct and incorrect explanations. Phys. Uspekhi 43, 1229–1252 (2000).
Mazzei, A. et al. Controlled coupling of counterpropagating whispering-gallery modes by a single Rayleigh scatterer: a classical problem in a quantum optical light. Phys. Rev. Lett. 99, 173603 (2007).
Gorodetsky, M. L. & Ilchenko, V. S. Optical microsphere resonators: optimal coupling to high-Q whispering-gallery modes. J. Opt. Soc. Am. B 16, 147–154 (1999).
Li, J., Liu, B., Hua, W. & Ma, Y. Effects of intermolecular forces on deep sub-10 nm spaced sliders. IEEE Trans. Magn. 38, 2141–2143 (2002).
Arita, Y., Mazilu, M. & Dholakia, K. Laser-induced rotation and cooling of a trapped microgyroscope in vacuum. Nat. Commun. 4, 2374 (2013).
Grier, D. G. A revolution in optical manipulation. Nature 424, 810–816 (2003).
Gross, W. A. et al. Fluid Film Lubrication (John Wiley and Sons, New York, 1980).
Busse, W. F. & Denton, W. H. Water-lubricated soft-rubber bearings. Trans. Am. Soc. Mech. Eng. 54, 3–10 (1932).
Blok, H. & Van Rossum, J. J. The foil bearing—a new departure in hydrodynamic lubrication. Lubr. Eng. 9, 316–320 (1953).
Eshel, A. Compressibility effects on the infinitely wide, perfectly flexible foil bearing. J. Lubr. Technol. 90, 221–225 (1968).
Eshel, A. & Elrod, H. G. Stiffness effects on the infinitely wide foil bearing. J. Lubr. Technol. 89, 92–97 (1967).
Langlois, W. E. The lightly loaded foil bearing at zero angle of wrap. IBM J. Res. Develop. 7, 112–116 (1963).
Jennings, S. G. The mean free path in air. J. Aerosol Sci. 19, 159–166 (1988).
Fukui, S. & Kaneko, R. Analysis of ultra-thin gas film lubrication based on linearized Boltzmann equation: first report—derivation of a generalized lubrication equation including thermal creep flow. J. Tribol. 110, 253–261 (1988).
Shen, S. & Chen, G. in Encyclopedia of Tribology (eds Wang, Q. J. & Chung, Y.-W.) 2309–2313 (Springer, New York, 2013).
Acknowledgements
We thank U. Hofi, Z. Katz, Y. Halupovich and B. Khachatryan for their help. This work was funded by the Israeli Centers for Research Excellence (I-CORE), ‘Circle of Light’ Excellence Center, the Israel Science Foundation (2013/15), the Israel Ministry of Science, Technology and Space, the MURI Center for Dynamic Magneto-Optics via the AFOSR Award number FA9550-14-1-0040, the Army Research Office (ARO) under grant number 73315PH, the AOARD under grant number FA2386-18-1-4045, the CREST under grant number JPMJCR1676, the IMPACT programme of JST, the RIKEN-AIST Challenge Research Fund, the JSPS-RFBR under grant number 17-52-50023, and the Sir John Templeton Foundation.
Reviewer information
Nature thanks A. Alù and M. Levy for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
S.M. and R.D. performed the experiments. A.U.H., H.J., F.N., E.M., Y.K. and D.N.C. performed the theoretical analysis. T.C. supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Rights and permissions
About this article
Cite this article
Maayani, S., Dahan, R., Kligerman, Y. et al. Flying couplers above spinning resonators generate irreversible refraction. Nature 558, 569–572 (2018). https://doi.org/10.1038/s41586-018-0245-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0245-5
This article is cited by
-
Exceptional points and non-Hermitian photonics at the nanoscale
Nature Nanotechnology (2023)
-
Higher-order singularities in phase-tracked electromechanical oscillators
Nature Communications (2023)
-
Phase-controlled asymmetric optomechanical entanglement against optical backscattering
Science China Physics, Mechanics & Astronomy (2023)
-
Auxiliary-Cavity-Induced Ultrasensitive and Ultrahigh-Resolution Biomolecule Mass Sensing in a Hybrid Spinning Resonator System
Journal of Russian Laser Research (2023)
-
Nonreciprocal generation of Schrödinger cat state induced by topology
Science China Physics, Mechanics & Astronomy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.