Main

Although transport-based diagnostics of static quantum phases1,2,3,4 generally reveal anomalous transport regimes only if the system is fine-tuned to a critical point5,6,7,8, externally driven quantum matter9 can exhibit exotic states with no equilibrium counterpart. As we demonstrate in this work, driven systems can thus open up the exploration of new states of matter characterized by an intricate interplay of fractal structure and quantum dynamics.

The time-independent Aubry–André–Harper (AAH) Hamiltonian10,11 describes particles hopping in a one-dimensional lattice with quasiperiodic pseudo-disorder. This paradigmatic model of quantum transport and quantum Hall phenomena exhibits Hofstadter butterfly energy spectra and hosts multifractal eigenstates only at a duality-protected localization phase transition10,11,12,13. If the incommensurate potential is applied instead as brief periodic kicks, the resulting ‘occasional quasicrystal’ described by the kicked Aubry–André–Harper (kAAH) model epitomizes the interplay between disorder and driving in quantum matter. Although pioneering experiments in various platforms have explored static and sinusoidally driven AAH models and incommensurate kicked rotors14,15,16,17,18,19,20, the kAAH model has previously been explored only theoretically21,22,23,24,25,26,27,28.

We demonstrate experimentally that the kAAH model exhibits signatures of anomalous transport across an extended range of parameter space, in agreement both with numerical calculations and with theoretical expectations for related models21,22,23,24. This letter reports three interconnected advances. The first is the experimental realization of the kAAH model itself. The second is the development of apodized Floquet engineering techniques that use spectrally tailored pulses to extend the accessible parameter range of our quantum simulator into the region where an extended regime of anomalous transport is theoretically expected. The third main advance is the measurement of the global phase diagram of the kAAH model, which reveals re-entrant delocalization and an extended parameter regime of anomalous transport that we argue theoretically is a consequence of multifractal states.

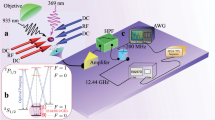
The experiments begin by loading a Bose–Einstein condensate (BEC) of a tunable number of 84Sr atoms (typically around 2 × 105) into the ground band of a 10Er-deep primary optical lattice, where \({E}_{{{{\rm{r}}}}}={h}^{2}/2m{\lambda }_{{{{\rm{P}}}}}^{2}\) is the recoil energy, m is the atomic mass, h is Planck’s constant and λP = 1,063.9774(23) nm is the primary lattice laser wavelength. To implement the kAAH Hamiltonian, pulsed incommensurate pseudo-disorder is realized by periodically applying a separate overlapped optical lattice of wavelength λS = 914.4488(17) nm. The kAAH Hamiltonian thus realized is given in the tight-binding approximation by

$$\hat{H}=-J\sum_{i=1}^{L}\left({\hat{b}}_{i}^{{\dagger} }{\hat{b}}_{i+1}+{{{\rm{h.c.}}}}\right)+F(t)\Delta\sum_{i=1}^{L}\cos (2\pi \alpha i+\varphi ){\hat{b}}_{i}^{{\dagger} }{\hat{b}}_{i},$$
(1)

where J = 0.0192Er ≈ h × 40 Hz is the tunnelling energy, which gives rise to a tunnelling time TJ = ℏ/J = (1/2π) × 25 ms, \({\hat{b}}_{i}({\hat{b}}^+_{i})\) is the bosonic annihilation (creation) operator at the i-th lattice site, Δ is the disorder strength, α = λP/λS is the wavelength ratio of the two lattices, φ is the relative phase of the two lattices, and F(t) = ∑nfτ(t − nTP) is the waveform of a periodic pulse train composed of finite-width, unit-height pulses with an effective pulse width τ = ∫ fτ(t) dt and pulse interval TP (Supplementary Information section II). As we will discuss, proper selection of the form of fτ(t) is crucial for exploring the majority of the phase diagram. We study the phase diagram in a two-dimensional parameter space with dimensionless axes T = TP/TJ = TPJ/ℏ and Λ = Δ/Δτ = Δτ/ℏ, which characterize the kick period and kick strength, respectively. To map out this phase diagram, we measure the long-time evolution of the density distribution of an initial tightly confined wave packet for different T and Λ using in situ absorption imaging14,29,30.

Theory predicts a rich phase diagram for this experimentally unexplored model26,27. In the high-frequency limit (1/T ≫ 1), the model reduces to the static AAH Hamiltonian. Much richer behaviours emerge at larger values of T and Λ (Fig. 1a,b). Numerically analysing the inverse participation ratio (IPR) \(\sum\nolimits_{j = 1}^{L}| {\psi }_{j}{| }^{4} \approx{L}^{-\xi }\) of single-particle position-space eigenstates ψj, we find four regimes in the (Λ, T) plane, in agreement with previous analyses of the equivalent quantum chaotic kicked Harper model21,22,23,24,25,31. The regime with T ≫ Λ is a completely delocalized phase in which the IPR exponent averaged over all states \(\overline{\xi }=1\). This and a duality mapping (Supplementary Information section I B) implies a localized phase (\(\overline{\xi }=0\)) for T ≪ Λ. Between these two limits, for sufficiently large T and Λ, there is an extended parameter range in which localized and delocalized states coexist in an intricate nested pattern with a finite fraction of multifractal states (Extended Data Fig. 1)25,31. At constant T (for example, T = 1.5), the predicted average IPR exponents and fraction of localized states can depend non-monotonically on Λ, suggesting the possibility of anomalous ‘re-entrant’32 states in which continuously increasing disorder strength can drive localization, then delocalization and then re-localization. In the thermodynamic limit, multifractality is theoretically expected to persist along the self-dual line 2T = Λ and in a region of measure zero with a complex shape (Supplementary Information section IV B 5)21,22,23,24,25,31. However, the fraction of multifractal states becomes vanishingly small only for extremely large system sizes of 107 sites25,31. For system sizes relevant to our experiment and even to many conceivable condensed-matter experiments, our theoretical results clearly predict a non-zero fraction of multifractal states in an extended parameter range away from the duality line. This is consistent with earlier studies that had suggested that an extended multifractal regime persists in the thermodynamic limit24. The existence and form of this anomalous regime are crucial for understanding our experimental measurements of the kAAH phase diagram. In particular, theory predicts that anomalous transport and re-entrant localization/delocalization transitions should emerge when T, Λ/2 ≳ 1.

Fig. 1: Phase diagram of the kAAH model and experimental approach.
figure 1

a, Average IPR scaling exponent \(\bar{\xi }\) as a function of Λ and T, for α = 1.162842. b, Standard deviation of IPR scaling exponents. Along the diagonal (Λ/T = 2), the scaling exponents for all eigenvectors take a single value. c, Schematic of the experiment. d, Experimental sequence. AA, Aubry–André.

Full size image

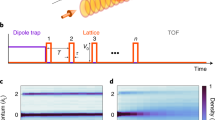
Figure 2 encompasses the first main result of our work: the experimental realization of the kAAH model. Figure 2a,b show the measured density evolution at two points in the phase diagram, one localized and one delocalized. The late-time width clearly distinguishes the two phases. The exponent γ characterizing the time evolution of the width σx of the density distribution (σx ∝ tγ for large t) provides another diagnostic, with γ near 1 indicating delocalization and γ near zero indicating localization (Fig. 2c). Deviations of measured values from exactly one or zero may be attributed to the finite duration of the experiment or to interparticle interactions, as discussed in Supplementary Information section II B. Figure 2d demonstrates the first experimental exploration of a swath of the kAAH phase diagram, obtained by measuring the late-time width of the atomic density distribution for a range of values of T and Λ both ≪1, using a simple rectangular form for the kick pulse shape fτ(t). In accordance with expectations for this high-frequency regime, we observe a period-dependent localization transition near the Aubry–André critical point at Λ/T = 2. However, our quantum simulator using a rectangular fτ(t) breaks down at values of T and Λ a hundred times smaller than those where the anomalous transport regime is predicted to emerge, due to higher-band excitations that invalidate the single-band approximation implicit in the kAAH model. This breakdown is visible in the cross-hatched data points near the upper right of Fig. 2d, which are (Λ, T) pairs where the density distribution failed experimental cuts (Supplementary Information section III A) on signal-to-noise ratio and centre position, indicating severe heating. Such interband heating prevents experimental access to the rich anomalous transport regime of the kAAH phase diagram; however, as we show next, this challenge can be overcome.

Fig. 2: Realizing the kAAH model in the high-frequency regime.
figure 2

a,b, Time sequence of density profiles in the kicked lattice for Λ/T below (a) or above (b) the localization transition. c, Fitting expansion curves to a form that captures both short- and long-time behaviour at various (Λ, T) allows for measurement of the exponent γ. The curves are for the data in a and b. The extracted widths were fit to \({\sigma }_{x}(t)={\sigma }_{0}{(1+t/{t}_{0})}^{\gamma }\), the solution to a generalized diffusion equation (Supplementary Information section III B). d, Measured localization phase diagram of the kAAH model for small Λ and T, using a simple rectangular form for the pulse shape fτ(t) with τ = 1 μs. The colour map depicts the fitted width of the density distribution σx as a function of Λ and T at thold = 2 s. The dashed line indicates the time-averaged static Aubry–André transition at Λ/T = 2. The centre point (white) of the colour map is set to the σx observed at the same hold time when the expansion exponent is in the centre of its transition from localized to delocalized values. Black crosses indicate the (Λ, T) values of the data in a, b and c. Cross-hatched pixels indicate data that failed cuts of the fitting procedure (Supplementary Information section III A) due to heating by interband transitions. Without mitigative measures, such heating prevents exploration of the phase diagram much beyond the region shown here. See Fig. 3 for details of the characterization and suppression of this effect. Max., maximum; Min., minimum; OD, optical density.

Full size image

To extend the kAAH quantum simulator to the regime of the phase diagram with T, Λ/2 ≳ 1 where anomalous behaviour is predicted, we developed a spectrally tailored (‘apodized’) Floquet engineering technique, which is the second main result of this work and which may prove useful in other contexts. Apodization is a filtering technique common in areas from optics to radio-frequency engineering. Here, we perform an analogous procedure by changing the shape of the pulse function fτ(t), thereby modifying the spectrum of the kicking waveform. The goal is to eliminate the population transfer to excited bands, which breaks the single-band assumption of the kAAH model. Figure 3a demonstrates the origin of this problem. Values of TP higher than a few tens of microseconds give rise to the rapid decay of ground-band atoms. Peaks in the decay rate match numerically calculated rates of interband transfer, suggesting that the root cause of the heating is the overlap of the spectrum of the kicking waveform with interband transition frequencies (see also Extended Data Figs. 2 and 3). We investigated two approaches for eliminating the interband heating: (1) conventional apodization with a Gaussian window function and (2) spectral filtering of the pulse train to specifically remove interband transition frequencies. In both cases, the time-domain pulse shape fτ(t) is renormalized to give equivalent pulse areas. Figure 3b,c shows the power spectra of different pulse shapes (square, Gaussian and spectrally filtered), superimposed (b) and integrated (c) over the frequency ranges of interband transitions, indicating that pulse shaping can address the problem of interband heating. Figure 3d shows experimental results for the density evolution with the three different pulse shapes for different pulse lengths τ, demonstrating the substantially better performance of shaped pulses, and Fig. 3e shows the measured decay rate for different pulse shapes, kick periods and repetition rates. Longer lifetimes are consistently achieved by spectrally engineering the kicking pulse shape. For the kAAH model, apodized Floquet engineering is absolutely required for accessing the non-trivial regions of the phase diagram at large T and Λ with quantum gas experiments.

Fig. 3: Apodized Floquet engineering.
figure 3

a, Decay rate of atoms kicked by square pulses with a pulse duration of τ = 1 μs and a kick strength of Λ = 0.018 for thold = 2 s as a function of kick period TP. The solid curve is the result of a numerical calculation (Supplementary Information section IV A). Arrows indicate the dominant transitions from the ground band \(\left\vert n=0\right\rangle\) to excited bands \(\left\vert n=1,2,\ldots \right\rangle\) (see also Extended Data Fig. 2). Error bars represent 95% confidence intervals from an exponential fit to 20 measurements. b, Form of the power spectrum of square (top), Gaussian (middle) and filtered (bottom) pulses. Shaded areas represent interband transitions. The frequency comb spacing is not drawn to scale for visibility. c, Net power in frequency ranges corresponding to interband transitions for square, Gaussian and filtered pulses of two pulse widths, each with period TP = 1 ms. For longer pulses, the Gaussian pulse already has little power in the interband transition frequencies and so filtering has little additional effect. d, Measured density profile at various times for each pulse shape. e, Measured decay rates from the ground band for different pulse shapes at various values of TP and τ. The baseline of each symbol corresponds to the measured decay rate. Error bars represent 95% confidence bounds from an exponential fit. a.u., arbitrary units.

Full size image

Figure 4a shows phase map data from such an apodized quantum simulator including the predicted anomalous transport regime. Although the time-averaged Aubry–André phase transition at Λ/T = 2 is visible for small T, areas of anomalous localization and delocalization appear at larger T, in qualitative agreement with theoretical predictions. As the disorder strength is increased for T > 1.5, the system appears to localize. Then it exhibits re-entrant disorder-driven delocalization and finally localizes again at strong disorder. Both these features agree with phase maps of an equivalent measurement on a numerically simulated kAAH model, shown in Fig. 4b. A simpler but less experimentally motivated map of the same numerical results appears in Extended Data Fig. 4, which maps the second moment of the density distribution without any convolution or fit. Although the fine details of the phase map depend on the specific quantity plotted, features like the small-T Aubry–André transition, the anomalous regime and re-entrant delocalization are always observed. To further investigate this newly realized state of driven matter, we measured the full expansion dynamics at selected points on the phase diagram. The transport scaling exponent γ serves as a signature of localized, delocalized and multifractal states in the kAAH model (Supplementary Information section IV B 6)22,29,30. Transport can also be diagnosed in the numerics by the time evolution of the IPR of the real-space density profile (Supplementary Information section IV B 2). As shown in Fig. 4c, across a broad swath of the phase diagram, the transport exponent lies between 0.4 and 0.6, which, based on the results of our theoretical calculations, we attribute to the presence of multifractal states. Our experimental observations accord with theoretical predictions also plotted in Fig. 4c. Here we note two important subtleties. First, states in the regime between the completely localized and completely delocalized areas have mixed character (Fig. 4d), and for any non-zero fraction of delocalized states, transport at the longest timescales is expected to be ballistic. However, for experimentally relevant system sizes, the theoretically predicted presence of multifractal states leads to sub-ballistic transport persisting up to timescales much longer than those explored experimentally (Supplementary Information section IV B 5). Second, note that continuously varying transport exponents can also arise in disordered systems due to rare regions in which the system locally resembles a localized state33. However, in a quasiperiodic system such as ours, such rare regions do not exist34.

Fig. 4: Experimental signatures of anomalous localization in the kAAH model.
figure 4

a, Measured phase diagram of the kAAH model for large T and Λ using apodized kicking waveforms (equivalent to a Gaussian with τ = 319.3 μs). The colour map shows the fitted width of the density distribution σx for thold = 2 s. The dashed line indicates the time-averaged static AAH transition at Λ/T = 2. The colour map centre (white) is chosen at this transition point as in Fig. 2d. b, Calculated phase diagram of the kAAH model for parameters and observable chosen to match the experiment. Numerically calculated time-evolved density distributions were convolved with the estimated point spread function of our imaging system and fitted with a Gaussian. The colour bar shows the fitted width and has the same limits as a. c, Expansion exponent γ versus Λ − Λ0 (diamonds) for parameter values indicated by points in a, extracted by fitting the late-time width evolution to σx(t) ∝ tγ. Error bars show 95% confidence bounds from such a fit to 16 measurements The measured σx is also plotted (squares), indicating that this single measurement tracks well with fits of the full time series. Equivalent expansion exponent data for the horizontal dot-dashed line in a appears in Extended Data Fig. 5. NI, noninteracting. d, Scaling exponent ξ of the IPR for single-particle states as a function of disorder strength Λ for the same parameter range. m/L denotes the normalized index of eigenstates.

Full size image

These results represent the first experimental glimpse, to our knowledge, of the rich phase diagram of a prototypical model of localization in driven quantum matter. The simple but unexpectedly powerful apodization techniques we demonstrate could be applied in a broad range of contexts and may enhance the range of quantum simulators in any situation in which a kicked system emulates a single-band model35. The results raise several fascinating questions for future investigation. How can multifractality and extended criticality be directly experimentally probed? Is the observed anomalous regime stable against the introduction of interactions19,28,36 or the presence of gapless propagating modes such as phonons? Can the duality of the phase map be directly imaged? In the low-frequency regime, the Floquet Hamiltonian is generically long-ranged, and the appearance of an anomalous transport phase recalls predictions of such phases in Hamiltonians with long-range hopping37. This raises the possibility of engineering other long-range Hamiltonians using the techniques of apodized low-frequency Floquet engineering presented here, potentially allowing the study of phenomena unattainable with local Hamiltonians such as robust error-correcting quantum codes38. A final intriguing possibility for future work is the realization of related anomalous states in Floquet-engineered solids or solid-state heterostructures39.

Methods

Preparing the initial state

The experiments began by preparing a BEC of 84Sr by evaporation in a crossed dipole trap with trapping frequencies of 50 and 70 Hz in the horizontal and vertical directions, respectively. The BEC was adiabatically loaded over 250 ms into a primary optical lattice with an initial width of 6 μm. The lattice was formed by retro-reflecting a small portion of a 1,064 nm beam, thereby creating a lattice potential superimposed on a single-beam dipole trap. This non-reflected portion of the beam produced most of the transverse confinement with a transverse trapping frequency near 100 Hz and a weak longitudinal confinement with a trapping frequency near 0.3 Hz. The dynamics were initiated by suddenly removing the axial confinement due to the crossed dipole trap.

Implementing the kAAH Hamiltonian

The incommensurate kicking lattice formed by λS = 915 nm light was superimposed onto the primary lattice as a periodic pulse train. The pulse intensity, pulse width and pulse waveform were controlled by tailoring the radio-frequency waveform sent to the acousto-optic modulator used to modulate the 915 nm light intensity. Lattice depths were calibrated by Kapitza–Dirac diffraction. The depth of the primary lattice was stabilized to 10Er unless otherwise specified. The time-dependent depth of the kicking lattice was monitored by a photodiode and recorded. The 1,064 and 915 nm standing waves shared a retro-reflecting mirror, which passively stabilized the relative phase of the two lattices.

Generating apodized waveforms

To obtain driving waveforms that do not drive excitation to higher bands, unwanted frequency components were filtered out of initial trial waveforms (either Gaussian or square pulses) by repeated application of appropriate digital band-pass filters, setting negative amplitudes to zero for physical realizability. The resulting waveform was used as an envelope for the radio-frequency signal sent to the acousto-optic modulator that controlled the power of the kicking lattice beam. For large T values (TP > 1 ms), simply using a Gaussian waveform was equally effective, as shown in Fig. 3.

Data processing

The density distribution after a time evolution of up to 2 s in the kicked lattice was obtained by analysing in situ absorption images. The width of the distribution was extracted from a Gaussian fit to the transversely integrated density profile. Data were omitted (hashed points in Fig. 2a) if the centre position of this fit differed substantially from the mean and if the signal-to-noise ratio was less than 40% of the mean. These cuts were failed for experimental realizations that produced density profiles so sparse as to not be reliably fitted and analysed. This was generally due to atom loss associated with substantial transverse or higher-band excitation. As discussed in the manuscript and Supplementary Information, we were able to identify the specific excitations that were being resonantly driven for all areas where the cuts were failed. See Supplementary Information section III for quantitative details of this procedure.