Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Polygonal patterns of Faraday water waves analogous to collective excitations in Bose–Einstein condensates

Nature Physics volume 20, pages 287–293 (2024)Cite this article

Subjects

Abstract

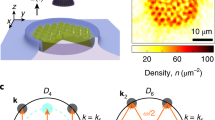
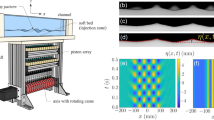
Since the discovery of crispations on a vibrating fluid layer, numerous types of patterns formed on fluid surfaces have been revealed. Here we report the observation of polygonal patterns of Faraday waves in vibrating water containers with parabolic and other concave bottoms. These patterns manifest themselves as simple geometric figures of symmetries ranging from elliptical up to heptagonal, with wavelengths much larger than the capillary length. Hence, they are intrinsically different from the previously studied patterns in vibrating drops or puddles and represent a particular variety of nonlinear shallow-water gravity waves or tidal waves in concave basins. Of specific interest is their resemblance to the collective excitations recently discovered in a driven Bose–Einstein condensate, not only sharing identical square-root scaling dispersion and pattern dynamics but also possessing similar nonlinear features like hard-spring nonlinearity. Based on the close correspondence, we propose an analogue of the patterning dynamics for classical and quantum fluid systems subject to confinement and argue that the analogy is mathematically valid even in the nonlinear regime.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Polygonal patterns of Faraday water waves.
Fig. 2: Measured parameters and properties of polygonal patterns.
Fig. 3: Polygonal patterns in fluids approaching ideal ones.
Fig. 4: Competition between the pentagonal and square modes.
Fig. 5: Numerical reproduction of polygonal patterns by integrating the unified equations (6a) and (6b).

Similar content being viewed by others

Data availability

The videos of selected experiments and simulations are provided with the supplementary materials.

Code availability

The OpenFOAM case files and the code for simulations of the unified model are available at https://github.com/lxynju/Polygon.

References

  1. Ellegaard, C. et al. Creating corners in kitchen sinks. Nature 392, 767–768 (1998).

    Article  CAS  ADS  Google Scholar 

  2. Morison, A., Labrosse, S. & Choblet, G. Sublimation-driven convection in Sputnik Planitia on Pluto. Nature 600, 419–423 (2021).

    Article  CAS  PubMed  ADS  Google Scholar 

  3. Noblin, X., Buguin, A. & Brochard-Wyart, F. Triplon modes of puddles. Phys. Rev. Lett. 94, 166102 (2005).

    Article  CAS  PubMed  ADS  Google Scholar 

  4. Singla, T. et al. Dynamics of a vertically vibrating mercury drop. AIP Adv. 9, 045204 (2019).

    Article  ADS  Google Scholar 

  5. Steen, P. H., Chang, C. T. & Bostwick, J. B. Droplet motions fill a periodic table. Proc. Natl Acad. Sci. USA 116, 4849 (2019).

    Article  CAS  PubMed  PubMed Central  ADS  Google Scholar 

  6. Bergen, J. E., Basso, B. C. & Bostwick, J. B. Leidenfrost drop dynamics: exciting dormant modes. Phys. Rev. Fluids 4, 083603 (2019).

  7. Shen, C. L., Xie, W. J. & Wei, B. Parametrically excited sectorial oscillation of liquid drops floating in ultrasound. Phys. Rev. E 81, 046305 (2010).

    Article  CAS  ADS  Google Scholar 

  8. Okada, M. & Okada, M. Observation of the shape of a water drop on an oscillating Teflon plate. Exp. Fluids 41, 789–802 (2006).

    Article  Google Scholar 

  9. Christiansen, B., Alstrom, P. & Levinsen, M. T. Ordered capillary-wave states: quasicrystals, hexagons, and radial waves. Phys. Rev. Lett. 68, 2157 (1992).

    Article  ADS  Google Scholar 

  10. Edwards, W. S. & Fauve, S. Patterns and quasi-patterns in the Faraday experiment. J. Fluid Mech. 278, 123 (1994).

    Article  MathSciNet  ADS  Google Scholar 

  11. Binks, D. & van de Water, W. Nonlinear pattern formation of Faraday waves. Phys. Rev. Lett. 78, 4043–4046 (1997).

    Article  CAS  ADS  Google Scholar 

  12. Staliunas, K., Longhi, S. & De Valcárcel, G. J. Faraday patterns in Bose-Einstein condensates. Phys. Rev. Lett. 89, 210406 (2002).

    Article  PubMed  ADS  Google Scholar 

  13. Maity, D. K. et al. Parametrically excited star-shaped patterns at the interface of binary Bose-Einstein condensates. Phys. Rev. A 102, 033320 (2020).

    Article  CAS  ADS  Google Scholar 

  14. Engels, P., Atherton, C. & Hoefer, M. A. Observation of Faraday waves in a Bose-Einstein condensate. Phys. Rev. Lett. 98, 095301 (2007).

    Article  CAS  PubMed  ADS  Google Scholar 

  15. Nguyen, J. H. V. et al. Parametric excitation of a Bose-Einstein condensate: from Faraday waves to granulation. Phys. Rev. X 9, 011052 (2019).

    CAS  Google Scholar 

  16. Zhang, Z., Yao, K.-X., Feng, L., Hu, J. & Chin, C. Pattern formation in a driven Bose-Einstein condensate. Nat. Phys. 16, 652–656 (2020).

    Article  CAS  Google Scholar 

  17. Kwon, K. et al. Spontaneous Formation of Star-Shaped Surface Patterns in a Driven Bose-Einstein Condensate. Phys. Rev. Lett. 127, 113001 (2021).

    Article  CAS  PubMed  ADS  Google Scholar 

  18. Stringari, S. Collective excitations of a trapped Bose-condensed gas. Phys. Rev. Lett. 77, 2360–2363 (1996).

    Article  CAS  PubMed  ADS  Google Scholar 

  19. Jin, D. S., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. A. Collective excitations of a Bose-Einstein condensate in a dilute gas. Phys. Rev. Lett. 77, 420–423 (1996).

    Article  CAS  PubMed  ADS  Google Scholar 

  20. Onofrio, R. et al. Surface excitations of a Bose-Einstein condensate. Phys. Rev. Lett. 84, 810 (2000).

    Article  CAS  PubMed  ADS  Google Scholar 

  21. Lamb, H. Hydrodynamics 6th edn, 291–293 (Cambridge Univ. Press, 1975).

  22. Westra, M. T., Brinks, D. J. & van de Water, W. Patterns of Faraday waves. J. Fluid Mech. 496, 1–32 (2003).

    Article  MathSciNet  ADS  Google Scholar 

  23. Rajchenbach, J., Clamond, D. & Leroux, A. Observation of star-shaped surface gravity waves. Phys. Rev. Lett. 110, 094502 (2013).

    Article  PubMed  ADS  Google Scholar 

  24. Hechenblaikner, G. et al. Observation of harmonic generation and nonlinear coupling in the collective dynamics of a Bose-Einstein condensate. Phys. Rev. Lett. 85, 692 (2000).

    Article  CAS  PubMed  ADS  Google Scholar 

  25. Landau, L. Theory of the superfluidity of helium II. Phys. Rev. 60, 356 (1941).

    Article  CAS  ADS  Google Scholar 

  26. Bogoliubov, N. N. On the theory of superfluidity. J. Phys. (USSR) 11, 23 (1947).

    MathSciNet  Google Scholar 

  27. Saint-Jalm, R. et al. Dynamical symmetry and breathers in a two-dimensional Bose gas. Phys. Rev. X 9, 021035 (2019).

    CAS  Google Scholar 

  28. Fultz, D. An experimental note on finite-amplitude standing gravity waves. J. Fluid Mech. 13, 193–212 (1962).

    Article  ADS  Google Scholar 

  29. Benjamin, T. B. & Ursell, F. The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. Ser. A 225, 505–515 (1954).

  30. Ciliberto, S. & Gollub, J. P. Chaotic mode competition in parametrically forced surface waves. J. Fluid Mech. 158, 381–398 (1985).

    Article  MathSciNet  ADS  Google Scholar 

  31. Meron, E. & Procaccia, I. Theory of chaos in surface waves: the reduction from hydrodynamics to few-dimensional dynamics. Phys. Rev. Lett. 56, 1323 (1986).

  32. Feng, Z. C. & Sethna, P. R. Symmetry-breaking bifurcations in resonant surface waves. J. Fluid Mech. 199, 495 (1989).

    Article  MathSciNet  ADS  Google Scholar 

  33. Kambe, T. & Umeki, M. Nonlinear dynamics of two-mode interactions in parametric excitation of surface waves. J. Fluid Mech. 212, 373–393 (1990).

    Article  MathSciNet  ADS  Google Scholar 

  34. Stoker, J. J. Water Waves: The Mathematical Theory with Applications, Vol. 36 (John Wiley & Sons, 1992).

  35. Ursell, F. The long-wave paradox in the theory of gravity waves. Math. Proc. Camb. Philos. Soc. 49, 685 (1953).

    Article  MathSciNet  ADS  Google Scholar 

  36. Mei, C. C. & Le Méhauté, B. Note on the equations of long waves over an uneven bottom. J. Geophys. Res. 71, 393 (1966).

    Article  MathSciNet  ADS  Google Scholar 

  37. Katopodes, N. D. & Wu, C. T. A model for unidirectional water waves. J. Eng. Mech. 112, 697 (1986).

    Article  Google Scholar 

  38. Thacker, W. Some exact solutions to the nonlinear shallow-water wave equations. J. Fluid Mech. 107, 499 (1981).

    Article  MathSciNet  ADS  Google Scholar 

  39. Whitham, G. B. Nonlinear effects in edge waves. J. Fluid Mech. 74, 353–368 (1976).

    Article  MathSciNet  ADS  Google Scholar 

  40. Liang, Q. & Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 32, 873–884 (2009).

    Article  ADS  Google Scholar 

  41. Wang, Y., Liang, Q., Kesserwani, G. & Hall, J. W. A 2D shallow flow model for practical dam-break simulations. J. Hydraul. Res. 49, 307–316 (2011).

    Article  Google Scholar 

  42. Liang, Q. & Borthwick, A. G. Adaptive quadtree simulation of shallow flows with wet-dry fronts over complex topography. Comput. Fluids 38, 221–234 (2009).

    Article  MathSciNet  CAS  Google Scholar 

  43. Fraccarollo, L. & Toro, E. F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydraul. Res. 33, 843–864 (1995).

    Article  Google Scholar 

  44. Bush, J. W. M. Pilot-wave hydrodynamics. Annu. Rev. Fluid Mech. 47, 269–292 (2015).

    Article  MathSciNet  ADS  Google Scholar 

  45. Sáenz, P. J. et al. Emergent order in hydrodynamic spin lattices. Nature 596, 58–62 (2021).

    Article  PubMed  ADS  Google Scholar 

  46. Yeh, H. H. Experimental study of standing edge waves. J. Fluid Mech. 168, 291–304 (1986).

    Article  ADS  Google Scholar 

  47. Guéry-Odelin, D. & Stringari, S. Scissors mode and superfluidity of a trapped Bose-Einstein condensed gas. Phys. Rev. Lett. 83, 4452–4455 (1999).

    Article  ADS  Google Scholar 

  48. Maragò, O. M. et al. Observation of the scissors mode and evidence for superfluidity of a trapped Bose-Einstein condensed gas. Phys. Rev. Lett. 84, 2056–2059 (2000).

    Article  PubMed  ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge S. Guo for her help with the experiments. This work was supported by the National Science Foundation of China under Grant No. 12174191. We are grateful to the High Performance Computing Center of Nanjing University for carrying out the simulations on its blade cluster system.

Author information

Authors and Affiliations

  1. Institute of Acoustics and Key Laboratory of Modern Acoustics (MOE), Nanjing University, Nanjing, P. R. China

    Xinyun Liu & Xinlong Wang

Authors
  1. Xinyun Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xinlong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

X.W. supervised the research. X.W. and X.L. conceived the experiments. X.L. performed the experiments and simulations. X.W. and X.L. analysed the data and wrote the paper.

Corresponding author

Correspondence to Xinlong Wang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Leonardo Gordillo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Discussion, Figs. 1–10 and Table 1.

Supplementary Video 1

Experimental observation of polygonal patterns in a relatively small paraboloidal container of diameter 20 cm.

Supplementary Video 2

Experimental observation of polygonal patterns in a large Chinese steel pan of diameter 50 cm.

Supplementary Video 3

Direct numerical simulation based on Navier–Stokes equations for real water exactly as same as the experiment in Supplementary Video 1 and for ideal fluid of no dissipation.

Supplementary Video 4

Simulation of the unified equations (6a) and (6b) in the main text.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, X., Wang, X. Polygonal patterns of Faraday water waves analogous to collective excitations in Bose–Einstein condensates. Nat. Phys. 20, 287–293 (2024). https://doi.org/10.1038/s41567-023-02294-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-023-02294-y

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing