Abstract
Recently, there has been increasing interest in the temporal degree of freedom in photonics due to its analogy with spatial axes, causality and open-system characteristics. In particular, the temporal analogues of photonic crystals have allowed the design of momentum gaps and their extension to topological and non-Hermitian photonics. Although recent studies have also revealed the effect of broken discrete time-translational symmetry in view of the temporal analogy of spatial Anderson localization, the broad intermediate regime between time order and time uncorrelated disorder has not been examined. Here we theoretically investigate the inverse design of photonic time disorder to achieve optical functionalities in spatially homogeneous platforms. By developing the structure factor and order metric using causal Green’s functions for disorder in the time domain, we propose an engineered time scatterer, which provides unidirectional scattering with controlled scattering amplitudes. We also show that the order-to-disorder transition in the time domain allows the manipulation of scattering bandwidths, which makes resonance-free temporal colour filtering possible. Our work could advance optical functionalities without spatial patterning.
Similar content being viewed by others
Main
Associating temporal and spatial axes has enriched the perspective on manipulating wave phenomena. Owing to the space–time analogy between the electromagnetic paraxial equation and the Schrödinger equation, the temporal axis can be considered an alternative or auxiliary axis to the spatial dimension. This similarity between temporal and spatial axes has established the fields of quantum-optical analogy1, non-Hermitian2, topological3,4 and supersymmetric5,6 photonics, and universal linear optics7. On the other hand, the uniqueness of a temporal axis has also been a recent research focus for achieving distinct design freedom8,9 from spatial ones, such as the control of translational, rotational or mirror symmetries. For example, broken time-translational symmetry results in dynamical wave responses, which require the open-system configuration: energy or matter exchange with the system environment. In this context, dynamical wave devices with optical nonlinearity10,11 or non-Markovian processes12 require the design strategy to appropriately break the time-translational symmetry. Furthermore, causality leads to unique scattering distinct from its spatial counterpart, completely blocking backscattering along the temporal axis13.
Recent studies utilizing temporal degrees of freedom have thus focused on exploiting similarities and differences between temporal and spatial axes. The discrete time-translational symmetry in photonic time crystals (PTCs)14,15 has been examined as a temporal analogy of photonic crystals, revealing the unique phenomena along the temporal axis, such as momentum bandgaps and the localized temporal peak due to the Zak phase. The concept of disordered photonics has also been extended to the temporal axis, such as observing the statistical amplification and scaling of Anderson localization in uncorrelated disorder16,17. Various wave physics, such as amplification and lasing18,19, effective medium theory20, Snell’s law13, spectral funnelling21, supersymmetry22, parity–time symmetry23, non-reciprocity24 and metamaterials25,26,27,28, have also revealed the unique features and applications of the temporal axis inspired by its spatial counterparts. Nonetheless, these intriguing achievements cover only the partial regimes in microstructural statistics of temporal modulations, such as order with conserved symmetries14,15,18,19,22,23,29,30, and their breaking with finite defects13,24 or perturbations without any correlations16,17. When considering abundant degrees of freedom in material microstructures31, further attention on the intermediate regime between order and uncorrelated disorder for the temporal axis is mandatory.
In this Article, we propose the concept of engineered time disorder, which allows for the designed manipulation of light scattering. Starting from the theoretical framework for analysing spatial disorder, we build its temporal analogue by incorporating causality in the time axis, which allows for examining the relationship between the time structure factor, time-translational order metric and wave scattering. We demonstrate that the moulding of the structure factor enables the completely independent engineering of forward and backward scattering. By investigating the order-to-disorder transition in the temporal modulation of the system, we also enable bandwidth-engineering of unidirectional scattering, such as time disorder for broadband scattering and resonance-free colour filtering. Our result verifies the spatial-pattern-free design of conventional optical functionalities and represents a great advantage of time disorder in bandwidth-engineering with respect to time crystals.
Results
Temporal scattering
Consider a non-magnetic, isotropic and spatially homogeneous optical material with time-modulated relative permittivity ε(t). For the x-polarized planewave of the displacement field D(r, t) = exψ(t)eikz, where r, ψ, and k are the position vector, field amplitude and wavenumber, respectively, the governing equation is6,14,16
where c is the speed of light. Because k is conserved, according to spatial translational symmetry, equation (1) is the temporal analogy of the one-dimensional (1D) Helmholtz equation for spatially varying materials, exhibiting space–time duality28 by imposing the role of the optical potential on ε−1(t). To investigate the regime of weak scattering, we express the real-valued optical potential as α(t) ≡ ε−1(t) = αb[1 + Δα(t)], where αb is the potential at t → ±∞. With the assumption of weak perturbation over a finite temporal range, the time-varying component αbΔα(t) becomes analogous to the weakly perturbed permittivity in spatial-domain problems1. Notably, as those time-varying systems are open systems, the energy provided by the environment, Pin(t) = duEM0/dt, results in the non-conservative electromagnetic (EM) field energy14,16 uEM0(t) = [E*(t) · D(t) + H*(t) · B(t)]/4, where E is the electric field, H is the magnetic field, B is the magnetic flux density and the asterik denotes the complex conjugation.
For a given temporal variation of the system, we employ the harmonic incidence ψinc(t) = exp(−iωbt), where ωb = αb1/2kc is the optical frequency at t → ±∞. Under the first-order Born approximation32 with |Δα(t)| ≪ 1, the time-domain scattering field ψsca(t) becomes
where G(t; t′) is Green’s function for the impulse response of the temporal delta function scatterer δ(t − t′) (Supplementary Note 1).
Although equation (2) is identical to the 1D scattering problem in the spatial domain32, the uniqueness of the time-varying material is in selecting the mathematical form of the Green’s function among several candidates: the Feynman, retarded and advanced propagators33. Due to the unidirectional flow of time, the temporal Green’s function satisfies causality: G(t; t′) = 0 for t < t′. To fulfil the temporal boundary conditions for the displacement field and magnetic field at t = t′ (refs. 9,14), the analytical form of the retarded Green’s function for the temporal impulse becomes (Fig. 1a and Supplementary Note 2)
where Θ(t) is the Heaviside step function of Θ(t > 0) = 1 and Θ(t ≤ 0) = 0 (Supplementary Note 3). The Green’s function in equation (3) can be separated into G(t; t′) = GFW(t; t′) + GBW(t; t′) for GFW, BW(t; t′) = ±exp[±iωb(t − t′)]Θ(t − t′)/(2iωb), where each sign of ±ωb determines the propagation direction with the conserved k.
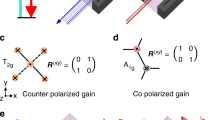
a,b, Schematics of temporal and spatial Green’s functions: Re[G(t; t′)e+ikz] (a) and Re[G(z; z′)e−iωt] (b). Shaded lines in a and b indicate the evolution of each Green’s function. c, Schematic of system modulation by signal power Pin(t) from the environment, representing the system gain and loss for positive and negative Pin, respectively. d, Energy alteration from light–matter interactions with the time disorder driven by Pin(t) in c. ε(t) (grey area) and uEM0(t) (purple line) are the time-varying permittivity confined inside the temporal range [0, T] and the instantaneous electromagnetic energy density, respectively.
We emphasize that causality imposes uniqueness on the temporal Green’s function, that is, the coexistence of the forward (or transmitted) and backward (or reflected) waves in t > t′ (Fig. 1a). Such a mathematical form of G(t; t′) is in sharp contrast to the spatial Green’s function, G(z; z′) ~ exp(ik|z − z′|), which exhibits the separate existence of the forward (e+ik(z − z′)) and backward (e−ik(z − z′)) waves in z > z′ and z ≤ z′, respectively (Fig. 1b). This uniqueness emphasizes the open-system nature of time-varying systems, despite the fact that the governing equation of equation (1) is mathematically analogous to the spatial one. When an external modulation to the system is applied by a time-varying signal power, Pin (Fig. 1c), the unique form of the causal Green’s function in a time-varying system—interfering forward and backward basis (Fig. 1a)—breaks the conservation of the EM energy inside the system (Fig. 1d). In this context, the independent control of forward and backward scattering in temporally random heterogeneous materials compels a design strategy distinct from their spatial counterparts.
From equations (2) and (3), the scattering field becomes (Supplementary Note 4)
Although the thermodynamic limit is an ideal criterion to characterize the statistical features of wave–matter interactions in disordered systems34, the non-conservative optical energy (Fig. 1d) may cause unphysical results, such as the divergence of the energy in momentum gaps15,17. Therefore, we assume a finite-range temporal variation Δα(t) with Δα(t < 0) = Δα(t > T) = 0 when examining equation (4). We also employ the ergodic hypothesis, that is, the statistical equivalence between the average over all realizations and the average over one statistically homogeneous realization at the thermodynamic limit34. Although the relationship between energy divergence and the common hypothesis of thermodynamic limit requires further study, the ergodicity allows for the homogeneous correlation function Ĉ(t1, t2) ≡ 〈Δα*(t1)Δα(t2)〉 = C(Δt) for 0 ≤ t1, 2 ≤ T and Δt = t1 − t2, where 〈.〉 denotes the ensemble average. We separate the ensemble-averaged scattering power after the temporal perturbation (t > T) into the forward (〈PFW〉) and backward (〈PBW〉) waves (Supplementary Note 5) as
With a sufficiently broad temporal range, each power approaches the Fourier transform of C(Δt), that is, \(S({\omega})={{{\mathcal{F}}}}[C(\Delta{t})]\) where \({{{\mathcal{F}}}}\) denotes the Fourier transform (Supplementary Note 6):
where we define S(ω) as the ‘time structure factor’ governing scattering from temporal disorder, that is, the temporal counterpart of the static structure factor34,35. It is worth mentioning that S(ω) is the power spectral density of the signal that determines the time-varying perturbation of an optical potential. While equation (6) allows for engineering forward and backward scatterings, we note that the condition of suppressing the forward wave 〈PFW〉 ~ 0 directly corresponds to the time-domain realization of the concept of hyperuniformity31,35,36,37,38,39,40,41, as S(ω → 0) ~ 0. It is worth mentioning that, although time-domain hyperuniformity has been observed in soft-matter physics, such as the avalanche size of the Oslo model42, to our knowledge, the corresponding phenomena and their engineering in wave physics have remained missing.
Therefore, engineering the power flows PFW, BW using time disorder is achieved by moulding S(ω) near ω = 0 and 2ωb. Notably, in the design of S(ω), three conditions should hold for C(Δt) and S(ω): the Hermiticity C(Δt) = C*(−Δt) with real-valued S(ω), |Re[C(Δt)]| ≤ C(Δt = 0) from the maximum of the correlation function, and S(ω) ≥ 0 from the autocorrelation theorem (Supplementary Note 7). We also note that we set 〈Δα(t)〉 = 0 to remove insuppressible scattering at the zero frequency limit35 S(ω = 0), which is the necessary condition to freely engineer the forward scattering power, PFW.
To establish the designed manipulation of light through photonic time disorder, we demonstrate the engineering of time disorder: unidirectional scattering for the independent control of 〈PFW〉 and 〈PBW〉, the order-to-disorder transition for spectral manipulation, and momentum-selective spectral shaping. We note that there are two different classes of one-to-many correspondence between a scattering response and the realizations of disorder. First, because scattering phenomena are governed by S(0) and S(2ωb) for a planewave of ωb, a family of time disorder can be achieved by altering the overall shape of S(ω) while preserving S(0) and S(2ωb). Second, even for the same S(ω), there are an infinite number of realizations of time disorder because the entire landscape is essentially uniquely determined by all the orders of correlation functions34. Therefore, to rigorously study the relationship between scattering and disorder, a number of different realizations with a given S(ω) should be examined. In the following discussion, we focus on the first origin in examining a family of disorder, as well as conducting the statistical analysis due to the second origin.
Unidirectional scattering
We demonstrate the unidirectional scattering achieved by suppressing S(0) or S(2ωb). We set a time scale t0 and assume incident frequency ωb = ω0. We set the structure factor functions SFW(ω) and SBW(ω) for the forward and backward scatterings, which are designed in the frequency ranges [−2ω0, 2ω0] and [−3ω0, 3ω0], respectively, and zero elsewhere. The structure factors SFW, BW(ω) in this scenario are modulated by the design parameters S0 = SFW(0) and S2ω = SBW(2ωb), respectively, while satisfying the continuity and C1 smoothness as well as the statistical bounds for ε(t) (Supplementary Note 8).
Figure 2a shows the designed SFW(ω) and SBW(ω) for different values of S0 and S2ω, respectively. With the corresponding C(Δt) from SFW, BW(ω), we generate a set of ε(t) realizations through the multivariate Gaussian process (Supplementary Notes 7 and 9). Three example realizations are depicted in Fig. 2b for the suppressions of (1) both forward and backward (case A), (2) backward only (case B) and (3) forward only (case D), which have the corresponding time structure factor shown in Fig. 2a.
a, Structure factors SFW(ω) (top) and SBW(ω) (bottom) with varying design parameters S0 and S2ω, respectively. The design parameters are represented by gradual colours (A, S0 = 0; B, S0 ≈ 2.95; C, S2ω = 0; D, S2ω ≈ 1.86). b, An example of the Δε(t) realizations (grey areas) and the corresponding scattering intensity |ψsca(t)|2 (solid lines) for the A, B and D states in a. t0 = 2π/ω0. c,d, Comparison of the scattering powers from the structure factor prediction (solid lines) and rigorous TD-TMM analysis (error bars) for each ensemble with different design parameters S0 and S2ω in a and b, showing suppression of the backward (c) and forward (d) scattering. The top and bottom figures represent the forward and backward power, respectively, after t > 20t0. Filled circles and error bars denote the ensemble average from the TD-TMM results and the interquartile range (IQR) of each ensemble of 104 realizations, respectively. Structure factors [SFW, BW(ω), S0, 2ω], scattering field (ψsca) and scattering powers (PFW, BW) are normalized with δ2/ω0, δ and δ2, respectively, where δ = [C(0)]1/2.
For each case, an ensemble of 104 realizations is generated, and their scattering responses are examined using the time-domain transfer matrix method (TD-TMM)16,43. Figure 2c,d shows that the ensemble average of the rigorous TMM results (error bars) provides good agreement with the S(ω)-based prediction with the Born approximation (lines). Engineering temporal modulation using the time structure factor allows for completely independent manipulation of temporal scattering: unidirectional scattering only with forward (case B) or backward (case D) propagations or scattering-free temporal variations (cases A and C).
Engineered time disorder for spectral manipulation
The main advantage of utilizing disordered systems in wave physics is the ability to manipulate multiple wave quantities with different sensitivities to material phases31. Such intricate wave–matter interactions allow for the alteration of the target wave quantity while preserving other ones, as shown in the independent manipulation of localization and spectral responses in spatial domains6,44. In this context, we focus on the independent control of two wave properties—scattering and spectral responses—using photonic time disorder.
In designing temporal systems through the language of the time structure factor, ordered systems (for example, photonic time crystals15) are depicted by a set of Bragg peaks, indicating certain harmonic frequencies at which the system interacts with an incident wave. In contrast, time disorder close to the Poisson process41 shows a broadband structure factor that guarantees a continuum frequency response; at the extreme, the uncorrelated Poisson disorder possesses the structure factor of an infinite plateau. Using such a clear distinction between order and uncorrelated disorder and the relationship between the structure factor and scattering, we explore the intermediate regime between two extremes in photonic time disorder.
To quantify the transition between order and uncorrelated disorder, we introduce the transition parameter ξ for the structure factor S(ω): from ξ = 0 mimicking crystals to ξ = 1 for a near-Poisson case. We set the extreme case of the structure factors SC(ω) and SP(ω) for the crystal and near-Poisson state, respectively, defining the transition between them (Fig. 3a and Supplementary Note 10) as
a, Schematics of the structure factors for crystalline (left) and near-Poisson disorder (right). ξ is the transition parameter between order (ξ = 0) and disorder (ξ = 1). b, Structure factors S(ω) for the order-to-disorder transition with varying ξ: from crystalline (navy) to near-Poisson (yellow). A, ξ = 0.025; B, ξ = 0.1; C, ξ = 0.3; D, ξ = 1. c, Examples of realizations of Δε(t) for A, C and D. d, Statistical relationship between the backward scattering power and the time-translational order metric τ. The scattering theory prediction (solid and dashed lines for equations (5) and (6), respectively) and rigorous TD-TMM (error bars) are compared for each ensemble. Error bars denote the IQR of each ensemble of 104 realizations. e,f, Spectral responses of the forward (e) and backward (f) scattering powers near the target momentum (0.9 < kc/ω0 < 1.1) for ensembles A, B and D in d. Solid lines and error bands denote the ensemble average and IQR of each ensemble of 104 realizations, respectively. Structure factors [S(ω)], order metric (τ) and scattering powers (PFW, BW) are normalized with δ2/ω0, δ4 and δ2, respectively, where δ = [C(0)]1/2.
Figure 3b shows the structure factors obtained from different mixing of SC(ω) and SP(ω), targeting the suppression of forward power PFW ~ 0 with S(0) = 0. As the transition from the A to D states occurs, the heights of the Bragg peaks from SC(ω) at ω ≠ 2ω0 decrease, while the bumps SP(ω) centred at ω = ±2ω0 (Fig. 3b, inset) are continuously broadened. Equation (7) allows for maintaining the integral of S(ω) over the frequency domain to restrict the average fluctuation in the time-domain realizations. The designed transition therefore enables the characterization of time disorder solely depending on the ‘pattern’ of disorder, not on the magnitude of the fluctuation.
Figure 3c shows examples of the realization of time disorder for different ξ values in Fig. 3b, all of which are designed to derive backward scattering only. The transition parameter ξ qualitatively describes the temporal material phase transition from nearly crystalline to nearly uncorrelated disorder. To characterize each disorder more quantitatively, we introduce the time-translational order metric τ:
where ±4ω0 denotes the range of non-zero S(ω) (Supplementary Note 10). Analogous to its original definition in the spatial domain35,41, τ characterizes the distance of a given temporal evolution from the Poisson process, describing how much a given ε(t) is ordered in the time domain. As shown in Fig. 3d, the designed backward scattering from equation (6) and the resulting TD-TMM show good agreement, while better agreement is achieved when we leave out the infinite temporal range approximation by using equation (5).
The most important difference between crystals and uncorrelated disorder can be found in their spectral responses. As shown in Fig. 3e,f, the change in material phases between order and uncorrelated disorder provides a designed manipulation of the bandwidth of temporal modulations while preserving the target scattering response: the suppression of forward scattering. Remarkably, near-Poisson time disorder (case D) guarantees almost ±10% range of spectrum bandwidth for the suppression of forward scattering and constant backward scattering, improving the bandwidth 40 times compared to that of the near-crystal one (case A). Therefore, the use of randomness in the temporal modulation enables a notable bandwidth enhancement and thus the noise-robust signal-processing preserving optical functionalities.
Momentum-selective spectral shaping
Through Figs. 2 and 3 we have demonstrated control of the scattering directivity under monochromatic conditions, as well as its spectral engineering through an order-to-disorder transition. Based on this result, we show a methodology for the filtering of light waves—the temporal ‘resonant-less’ colour filter—using a platform with spatial translational symmetry. The proposed approach is in sharp contrast to conventional platforms for light filtering, such as multilayers45 or resonators46.
As an example of this application, we consider the propagation of a pulse and its interaction with the designed photonic time disorder, which leads to unidirectional and bandpass scattering. Because the forward scattering is governed by S(0) regardless of the light momentum k, the momentum-resolved operation for forward scattering is prohibited. We thus focus on the filtering of backward waves while suppressing forward waves, which filters out the range of ‘wave’ momenta k by the corresponding ‘material’ temporal frequencies |ω| = 2c|k| ∈ [ωmin, ωmax] (= [ω0/2, ω0] in Fig. 4a). Notably, the non-zero lower bound ωmin, which imposes a stricter condition on suppressing the forward wave, comprises the temporal realization of the stealthy hyperuniformity35,41, as S(|ω| < ωmin) ~ 0. We also set S(ω) ~ ω−2 dependency in the target range to compensate for the ω2 dependency of the scattering power (equation (6)). The temporal correlation and a sample realization of a given structure factor are shown in Fig. 4b,c.
a, Target structure factor for momentum-dependent spectral shaping of backscattering. b,c, The corresponding temporal correlation function (b) and sample realization (c) of Δε(t). d,e, Time evolution of a Gaussian pulse Dinc(z, t = 0) = exp[−(z/σz)2/2] undergoing a tailored temporal perturbation from t/t0 = 10 to 90: total field amplitude (d) and scattering power (e). Arrows indicate the direction of propagation for the incident and back-reflected fields. f,g, Spectral responses of the scattering field: time evolution of the k-space field Dsca(k, t) (f) and the ω-domain field Dsca(z = 0, ω) at a fixed point (g). The blue dashed line in f denotes Dinc(z, t = 0). The shaded area in g represents the filtering band S(2ck). The gradual colours in d–f represent the time evolutions from t = 0 (black) to 100t0 (yellow). Structure factors S(ω) and fields Dsca(z), Dsca, inc(k) and Dsca(ω) are normalized with δ2/ω0, δ, δc/ω0 and δ/ω0, respectively, where δ = [C(0)]1/2. σz = ct0 in d–g.
The initial displacement field D(z, t = 0) is a real-valued scalar function that satisfies D(k) = D*(−k). We assume a Gaussian pulse D(z, t = 0) = exp[−(z/σz)2/2]. The time evolution of the field through the time disorder filter becomes
where ψtot(t; k) is the single-component response of the incident planewave ψinc(t) = e−ikct. Snapshots of the pulse evolution are shown in Fig. 4d, exhibiting +z propagation (pink arrow) and a scattered tail behind it.
The evolutions of scattered fields in real- and k-space are illustrated in Fig. 4e,f, respectively. After the modulation, the generated backscattered field propagates along the −z-direction (blue arrow). Figure 4f and its ω-axis representation (Fig. 4g) clearly demonstrate the filtering functionality, which preserves the envelope shape of the original incident pulse while suppressing the designed band stop range ck/ω0 ∈ [−1/4, 1/4] (Supplementary Video 1).
The mechanism of the suggested temporal colour filter is fundamentally distinct from conventional optical filters, which utilize the bounded momentum responses through spatial inhomogeneity (for example, using mirrors, scatterers or resonators) and the following constraint on spectral responses through dispersion relations. In contrast, the proposed temporal colour filter does not require spatial inhomogeneity. Although the momentum of light is preserved through spatial translational symmetry, the spectral responses are filtered through broken temporal translational symmetry, which is the nature of time-varying open systems.
Discussion
Recently, several important studies have explored time disorder16,17, revealing the growth of the statistical intensity of waves with log-normal distributions and temporal Anderson localization, both of which are obtained with uncorrelated disorder. In contrast, the importance of our result is the bridging of temporal light scattering and correlated time disorder, which allows for the deterministic engineering of scattering direction, bandwidth and spectral shaping.
In terms of time-dependent perturbation theory, our statistical approach corresponds to a weak perturbation with the spectral transition amplitude S(ω) that gives rise to the transition from incident (initial state, ωb) to forward or backward scattering (first-order perturbations, ±ωb) with energy differences S(Δω = −2ωb or 0), respectively, similar to Fermi’s golden rule. This is consistent with the so-called time correlation function in the Green–Kubo relationship47,48 that describes the transport coefficient in fluid49 or thermal50 systems. Although the listed phenomena all share the universal linear response theory in both classical and quantum physics, direct application of the essence of the Green–Kubo relation to temporal light scattering is demonstrated, and it serves as a toolkit for dynamical photonic systems.
Notably, time-varying wave systems can be realized experimentally through time-varying transmission lines (TVTLs)9,18,51,52,53,54 in the microwave regime. Because transmission lines are ideal platforms for describing 1D wave propagations, TVTLs with temporal modulations achieved via loaded LC resonators or varactor diodes allow for reproducing intriguing phenomena in time-varying wave systems. TVTLs are also expected to be a suitable platform for the practical implementation of our disordered systems, as they only require free-form control of time-varying parameters. Notably, the realization of photonic time disorder beyond the microwave regime is a much more challenging issue. Although the unidirectional scattering with suppressed forward scattering can be realized independently of the modulation speed (S(0) = 0), the engineering of backward scattering S(2ωb) requires ultrafast modulations, which is a controversial topic in recent studies on photonic momentum gaps55. For example, to achieve considerable modulation of backward scattering in the infrared or visible range, femtosecond modulation of optical refractive indices is necessary. All-optical modulation based on second-order55 or third-order optical nonlinearity is a possible mechanism. To increase the effective material perturbation in strong light–matter interactions, the use of two-dimensional materials56, plasmonic platforms57 or epsilon-near-zero metamaterials58 can be candidate platforms.
To summarize, we have developed the patternless realization of EM scattering in temporally disordered media. Starting from the analytical formulation of wave scattering with the time structure factor, we have demonstrated moulding of structure factors for engineered scattering. This top–down approach enables the design of modulation signals for unidirectional scattering in spatially homogeneous systems. By examining the order-to-disorder transition in the temporal domain, we have also developed bandwidth-engineering while preserving unidirectional scattering, which enables the realization of resonance-free colour filters. To develop a more concrete theoretical foundation of disordered photonics in the time domain, exploring the uniqueness and criteria of photonic time disorder, such as the energy non-conservative nature of momentum gaps with hyperuniformity35 and stealth31 and its relation to the thermodynamic limit and the necessity of finite-temporal-range analysis, will be a further research topic. In terms of engineered disorder, unidirectional scattering achieved with photonic time disorder will provide extended design freedom in realizing optical non-reciprocity59,60. To break Lorentz reciprocity60, the generalization of photonic time disorder to the spatio-temporal domain will be necessary. Bandwidth-engineering through the order-to-disorder transition, as shown in our work, will then be applicable for the realization of broadband optical isolation.
Data availability
Data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Code availability
All codes are available at GitHub (https://github.com/jmkim93/Temporal-Scattering).
References
Longhi, S. Quantum-optical analogies using photonic structures. Laser Photon. Rev. 3, 243–261 (2009).
Feng, L., El-Ganainy, R. & Ge, L. Non-Hermitian photonics based on parity-time symmetry. Nat. Photon. 11, 752–762 (2017).
Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Miri, M.-A., Heinrich, M., El-Ganainy, R. & Christodoulides, D. N. Supersymmetric optical structures. Phys. Rev. Lett. 110, 233902 (2013).
Yu, S., Piao, X., Hong, J. & Park, N. Bloch-like waves in random-walk potentials based on supersymmetry. Nat. Commun. 6, 8269 (2015).
Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).
Engheta, N. Metamaterials with high degrees of freedom: space, time and more. Nanophotonics 10, 639–642 (2021).
Galiffi, E. et al. Photonics of time-varying media. Adv. Photonics 4, 014002 (2022).
Nie, W. Optical nonlinearity - phenomena, applications and materials. Adv. Mater. 5, 520–545 (1993).
Leuthol, J., Koos, C. & Freude, W. Nonlinear silicon photonics. Nat. Photon. 4, 535–544 (2010).
Spagnolo, M. et al. Experimental photonic quantum memristor. Nat. Photon. 16, 318–323 (2022).
Plansinis, B. W., Donaldson, W. R. & Agrawal, G. P. What is the temporal analog of reflection and refraction of optical beams? Phys. Rev. Lett. 115, 183901 (2015).
Zurita-Sánchez, J. R., Halevi, P. & Cervantes-González, J. C. Reflection and transmission of a wave incident on a slab with a time-periodic dielectric function ϵ(t). Phys. Rev. A 79, 053821 (2009).
Lustig, E., Sharabi, Y. & Segev, M. Topological aspects of photonic time crystals. Optica 5, 1390–1395 (2018).
Carminati, R., Chen, H., Pierrat, R. & Shapiro, B. Universal statistics of waves in a random time-varying medium. Phys. Rev. Lett. 127, 094101 (2021).
Sharabi, Y., Lustig, E. & Segev, M. Disordered photonic time crystals. Phys. Rev. Lett. 126, 163902 (2021).
Park, J. et al. Revealing non-Hermitian band structures of photonic Floquet media. Sci. Adv. 8, eabo6220 (2022).
Lyubarov, M. et al. Amplified emission and lasing in photonic time crystals. Science 377, 425–428 (2022).
Pacheco-Peña, V. & Engheta, N. Effective medium concept in temporal metamaterials. Nanophotonics 9, 379–391 (2020).
Lee, K. et al. Resonance-enhanced spectral funneling in Fabry-Perot resonators with a temporal boundary mirror. Nanophotonics 11, 2045–2055 (2022).
García-Meca, C., Ortiz, A. M. & Sáez, R. L. Supersymmetry in the time domain and its applications in optics. Nat. Commun. 11, 813 (2020).
Li, H., Yin, S., Galiffi, E. & Alù, A. Temporal parity-time symmetry for extreme energy transformations. Phys. Rev. Lett. 127, 153903 (2021).
Li, H., Yin, S. & Alù, A. Nonreciprocity and Faraday rotation at time interfaces. Phys. Rev. Lett. 128, 173901 (2022).
Lukens, J. M., Leaird, D. E. & Weiner, A. M. A temporal cloak at telecommunication data rate. Nature 498, 205–208 (2013).
Pacheco-Peña, V. & Engheta, N. Temporal aiming. Light Sci. Appl. 9, 129 (2020).
Pacheco-Peña, V. & Engheta, N. Antireflection temporal coatings. Optica 7, 323–331 (2020).
Castaldi, G., Pacheco-Peña, V., Moccia, M., Engheta, N. & Galdi, V. Exploiting space-time duality in the synthesis of impedance transformers via temporal metamaterials. Nanophotonics 10, 3687–3699 (2021).
Park, J. & Min, B. Spatiotemporal plane wave expansion method for arbitrary space-time periodic photonic media. Opt. Lett. 46, 484–487 (2021).
Park, J. et al. Comment on ‘Amplified emission and lasing in photonic time crystals’. Preprint at arXiv https://arxiv.org/abs/2211.14832 (2022).
Yu, S., Qiu, C.-W., Chong, Y., Torquato, S. & Park, N. Engineered disorder in photonics. Nat. Rev. Mater. 6, 226–243 (2021).
Twersky, V. Multiple scattering of waves and optical phenomena. J. Opt. Soc. Am. 52, 145–171 (1962).
Peskin, M. E. & Schroeder, D. V. An Introduction to Quantum Field Theory (Addison-Wesley, 1995).
Torquato, S. Random Heterogeneous Materials: Microstructure and Macroscopic Properties (Springer, 2002).
Torquato, S. Hyperuniform states of matter. Phys. Rep. 745, 1–95 (2018).
Torquato, S. & Stillinger, F. H. Local density fluctuations, hyperuniformity and order metrics. Phys. Rev. E 68, 041113 (2003).
Batten, R. D., Stillinger, F. H. & Torquato, S. Classical disordered ground states: super-ideal gases and stealth and equi-luminous materials. J. Appl. Phys. 104, 033504 (2008).
Florescu, M., Torquato, S. & Steinhardt, P. J. Designer disordered materials with large, complete photonic band gaps. Proc. Natl Acad. Sci. USA 106, 20658–20663 (2009).
Florescu, M., Steinhardt, P. J. & Torquato, S. Optical cavities and waveguides in hyperuniform disordered photonic solids. Phys. Rev. B 87, 165116 (2013).
Man, W. et al. Isotropic band gaps and freeform waveguides observed in hyperuniform disordered photonic solids. Proc. Natl Acad. Sci. USA 110, 15886–15891 (2013).
Torquato, S., Zhang, G. & Stillinger, F. H. Ensemble theory for stealthy hyperuniform disordered ground states. Phys. Rev. X 5, 021020 (2015).
Garcia-Millan, R., Pruessner, G., Pickering, L. & Christensen, K. Correlations and hyperuniformity in the avalanche size of the Oslo model. EPL 122, 50003 (2018).
Yariv, A. & Yeh, P. Optical Waves in Crystals: Propagation and Control of Laser Radiation (Wiley, 2002).
Sheinfux, H. H., Kaminer, I., Genack, A. Z. & Segev, M. Interplay between evanescence and disorder in deep subwavelength photonic structures. Nat. Commun. 7, 12927 (2016).
Macleod, H. A. Thin-Film Optical Filters 4th edn (CRC Press, 2010).
Vahala, K. J. Optical microcavities. Nature 424, 839–846 (2003).
Green, M. S. Markoff random processes and the statistical mechanics of time-dependent phenomena. J. Chem. Phys. 20, 1281–1295 (1952).
Kubo, R. Statistical-mechanical theory of irreversible processes. 1. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 12, 570–586 (1957).
Alfè, D. & Gillan, M. J. First-principles calculation of transport coefficients. Phys. Rev. Lett. 81, 5161–5164 (1998).
Carbogno, C., Ramprasad, R. & Scheffler, M. Ab initio Green-Kubo approach for the thermal conductivity of solids. Phys. Rev. Lett. 118, 175901 (2017).
Lurie, K. A. & Yakovlev, V. V. Energy accumulation in waves propagating in space- and time-varying transmission lines. IEEE Antennas Wirel. Propag. Lett. 15, 1681–1684 (2016).
Taravati, S., Chamanara, N. & Caloz, C. Nonreciprocal electromagnetic scattering from a periodically space-time modulated slab and application to a quasisonic isolator. Phys. Rev. B 96, 165144 (2017).
Shlivinski, A. & Hadad, Y. Beyond the Bode-Fano bound: wideband impedance matching for short pulses using temporal switching of transmission-line parameters. Phys. Rev. Lett. 121, 204301 (2018).
Hadad, Y. & Shlivinski, A. Soft temporal switching of transmission line parameters: wave-field, energy balance and applications. IEEE Trans. Antennas Propag. 68, 1643–1654 (2020).
Hayran, Z., Khurgin, J. B. & Monticone, F. ℏω versus ℏk: dispersion and energy constraints on time-varying photonic materials and time crystals. Opt. Mater. Express 12, 3904–3917 (2022).
Kuttruff, J. et al. Ultrafast all-optical switching enabled by epsilon-near-zero-tailored absorption in metal-insulator nanocavities. Commun. Phys. 3, 114 (2020).
Taghinejad, M. et al. Hot‐electron‐assisted femtosecond all‐optical modulation in plasmonics. Adv. Mater. 30, 1704915 (2018).
Bohn, J. et al. All-optical switching of an epsilon-near-zero plasmon resonance in indium tin oxide. Nat. Commun. 12, 1017 (2021).
Yu, Z. & Fan, S. Complete optical isolation created by indirect interband photonic transitions. Nat. Photon. 3, 91–94 (2009).
Jalas, D. et al. What is—and what is not—an optical isolator. Nat. Photon. 7, 579–582 (2013).
Acknowledgements
We thank B. Min and Y. Jeong for helpful discussions on the realization of photonic time disorder beyond the microwave regime. This work was supported by the National Research Foundation of Korea (NRF) through the Basic Research Laboratory (no. 2021R1A4A3032027), Young Researcher Program (no. 2021R1C1C1005031) and Global Frontier Program (no. 2014M3A6B3063708), all funded by the Korean government.
Author information
Authors and Affiliations
Contributions
J.K., S.Y. and N.P. conceived the idea. J.K. developed the theoretical tool and performed the numerical analysis. J.K. and D.L. examined the theoretical and numerical analysis. All authors discussed the results and wrote the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes 1–10 and Supplementary Figs. 1–4.
Supplementary Video for Fig. 4.
Source data
Source Data Fig. 1
Data for Fig. 1.
Source Data Fig. 2
Data for Fig. 2.
Source Data Fig. 3
Data for Fig. 3.
Source Data Fig. 4
Data for Fig. 4.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, J., Lee, D., Yu, S. et al. Unidirectional scattering with spatial homogeneity using correlated photonic time disorder. Nat. Phys. 19, 726–732 (2023). https://doi.org/10.1038/s41567-023-01962-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-023-01962-3