Main

Microresonator solitons exist through a balance of optical nonlinearity and dispersion, which must be anomalous for bright soliton generation1,2,3. Moreover, microresonators must feature high optical Q factors for low pump power operation of the resulting microcomb. Although these challenges have been addressed at telecommunication wavelengths using a range of material systems1, ultra-low-loss Si3N4 resonators4,5 do not yet support bright solitons as their waveguides feature normal dispersion4. Furthermore, all resonator materials are dominated by normal dispersion at shorter wavelengths. Although it is possible to form normal dispersion combs6, the temporally short pulse nature and highly reproducible spectral envelopes of anomalous dispersion soliton combs1 have generated keen interest in methods to induce anomalous dispersion for bright soliton generation in normal dispersion systems. Such methods have in common the engineering of dispersion through coupling of resonator mode families, including those associated with concentric resonator modes7,8, polarization9,10 or transverse modes11,12. As an aside, such coupled resonators have also been used to improve normal dispersion comb formation13,14 and to boost the power efficiency of bright combs15.

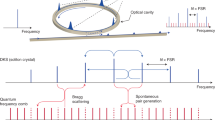
Here we engineer anomalous dispersion in ultra-low-loss Si3N4 resonators by partially coupling resonators (Fig. 1a). Such geometry introduces unusual new features to bright soliton generation; for example, spectra resembling single soliton pulse microcombs form instead from coherent pulse pairs (Fig. 1a). The pulse pairs circulate in a mirror-image-like fashion in the coupled rings to form coherent comb spectra (Fig. 1b) with highly stable microwave beat notes (Fig. 1c). The interaction of the pulses in the coupling section between the rings is shown to induce anomalous dispersion, which compensates for the overall normal dispersion of each ring. This pairwise compensation spectrally recurs, thereby opening multiple anomalous dispersion windows for the formation of multicolour soliton pairs. These windows can be engineered during resonator design. Furthermore, the spectral composition of each pulse in a pair is different. Figure 1b, for example, shows through- and drop-port spectra that reflect the distinct spectral compositions of pulses in rings A and B (Fig. 1a). This peculiar effect is also associated with Dirac solitons16 and it is shown that the two-ring pulse pair represents a new embodiment of a Dirac soliton as the underlying dynamical equation (see Methods) resembles the nonlinear Dirac equation in 1 + 1 dimensions. Pulse pairing is also extendable to higher-dimensional designs with additional normal dispersion rings. For example, in Fig. 1d–f, three pulses in three coupled rings alternately pair to compensate for the normal dispersion of each ring.

Fig. 1: Soliton pulse pair generation in two- and three-coupled-ring microresonators.
figure 1

a, Schematic showing coherent pulse pairs that form a composite excitation. The inset is a photomicrograph of the two-coupled-ring resonator used in the experiments. Rings A and B are indicated. Scale bar, 1 mm. b, Simultaneous measurements of optical spectra collected from the through (pumping port) and drop ports in the coupled-ring resonator of a. The measured mode dispersion is also plotted. Two dispersive waves are observed at spectral locations corresponding to the phase matching condition, as indicated by the dispersion curve. c, Radiofrequency spectrum of microcomb beatnote. RBW, resolution bandwidth. d, Illustration of three-pulse generation in a three-coupled-ring microresonator wherein pulses alternately pair. The inset is a photomicrograph of the three-coupled-ring microresonator used in the experiments. Scale bar, 1 mm. e, Measurement of optical spectrum of the three pulse microcomb. The measured mode dispersion is also plotted. f, Radiofrequency spectrum of the microcomb beatnote.

Full size image

In what follows, we first study the dispersion of this system and compare it with past mode coupling methods. Experimental results, including dispersion measurement and comb formation, are then presented. Pairwise pulse formation is then studied in the time domain. In presenting the results, it is convenient to resolve the ambiguity created by pulse-pair spectra in two- and three-coupled rings that nonetheless resemble single-pulse soliton spectra. To accomplish this, we denote these cases as bipartite and tripartite soliton microcombs, respectively. The need for such nomenclature is made clear by the demonstration of multiple pulse-pair states, including a two-ring microcomb state containing four pulses, which behaves as a two-pulse soliton crystal, and a three-ring state with 12 pulses, which behaves as a four-pulse soliton crystal17.

Recurring spectral windows

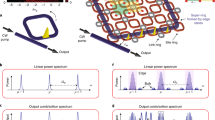
Before addressing pulse-pair propagation in the two- and three-ring systems, the conventional mode-family coupling approach is considered7,8,10. A concentric resonator system is chosen as a representative example (upper-left panel, Fig. 2a). The characteristics of this system are identical to other methods. First, a phase-matching condition must be satisfied such that the absolute mode number of each ring (or each coupled mode) must be equal at the same optical frequency. This mode number determines the wavelength at which soliton formation is possible. Second, the free-spectral-range values (FSRA and FSRB) of the uncoupled mode families of rings A and B must be close in value compared with their average FSR = (FSRA + FSRB)/2 so that phase matching occurs over a large number of modes. With these conditions satisfied, the resulting dispersion will be as illustrated schematically in Fig. 2a (lower panel, green curves). Comparisons with the uncoupled dispersion curves (centre dashed blue and red lines) show that anomalous dispersion is possible for the upper mode family branch.

Fig. 2: Mode number non-conservation coupling and dispersion for bright soliton formation.
figure 2

a, Dispersion properties for two resonator coupling schemes. Concentric rings (upper-left panel) induce coupling wherein the mode number is conserved. The centre blue and red dashed lines (lower panel) show that the resonance frequencies of the coupled rings have slightly different FSRs. A single coupling-induced gap is opened at their intersection (mode number M0), which corresponds to phase matching of the concentric ring modes. Two hybrid mode branches are thereby created (green curves) with a single anomalous dispersion window. In this work (top-right panel), inter-ring coupling occurs from resonance frequency matching instead of mode number matching (that is, mode number is not conserved). By contrast to the concentric case, dispersion is altered at all frequency degeneracies. Spectral folding (allowed by non-conservation of mode number) is illustrated by the multiple dashed lines (lower panel) and induces multiple gaps. These recur with period M (set by the Vernier in the FSRs) creating multiple anomalous dispersion windows. b, Measured frequency dispersion of the coupled resonator (green circles) versus the relative mode number μ. Here D1/(2π) = 19.9766 GHz, and ω0 is chosen so that μ = 0 is at the crossing centre (1,552.3 nm). Multiple anomalous dispersion windows appear around μ = 0 and 400 for the upper branch, and μ = −200 and 200 for the lower branch. The anomalous dispersion windows near μ = −200, 0 and 200 have been highlighted. Solid curves are fittings and the colour refers to the fractional energy contribution from ring A. The averages of the upper and lower branch mode frequencies are plotted as orange circles and fitted by a second-order dispersion model (orange curve, described by equation (1)). The inset is the transmission observed when scanning a laser over resonances in the anomalous dispersion windows. Soliton steps are observed around μ = −200, 0 and 200. c, Measured relative frequency dispersion of the coupled resonator (green circles) versus μ. Here D2/(2π) = −283.0 kHz, and the other parameters are the same as in b. Solid curves are the theoretical fittings described by equation (2). Fitted mode frequency dispersion diagrams of the single rings without coupling are shown as red and blue lines.

Full size image

Next consider the case in which two rings are placed side-by-side and coupled together (Fig. 2a, upper-right panel). The two ring cavities differ only in length, with ring B being slightly longer than ring A so that FSRA > FSRB. Considering the straight coupling section from a coupled-mode perspective, the modes of the two rings will strongly couple if they have matching wavevectors (or equivalently, resonance frequencies), whereas there are no requirements on mode number matching of the rings (that is, the mode number is not conserved). In comparison with the concentric ring configuration, this dramatically modifies the dispersion relation (Fig. 2a, lower panel, orange curves). Due to the loss of mode number conservation, inter-ring coupling pushes the resonance frequencies away from that of the individual rings (blue and red dashed lines) at all frequency degeneracies, so that recurring anomalous dispersion windows with period M = FSR/(FSRA − FSRB) now appear in the spectrum. These windows result from the spectral folding that occurs due to the frequency Vernier between the cavity resonances. As an aside, because the mode number is not conserved, modelling of this dispersion proceeds differently relative to the standard coupled-mode family approach (see Supplementary Information).

Dispersion measurements and soliton pulse pair generation

Two- and three-ring resonators consist of thin, single-mode Si3N4 waveguides (see the optical images in the insets of Fig. 1a,d). Bus waveguides provide external coupling. For the coupled two-ring device, the circumference of ring A is 9.5 mm (FSR ≈ 20 GHz), and ring B is 0.5% longer than ring A. For the three-ring device, the right-most ring has a circumference of 9.5 mm, and each other ring is 0.3% longer than its neighbour to the right. The rings feature high intrinsic Q factors exceeding 75 × 106. Individually, each ring does not support bright soliton formation at around 1,550 nm due to the strong normal dispersion associated with the low confinement waveguide structure (see Methods and Extended Data Fig. 1). Past studies on similar single-ring structures have generated only dark pulse comb spectra4.

The measured frequency dispersion (green points) for the two-ring system is compared with theory (solid lines) in Fig. 2b. The dispersion of the three-ring resonator is discussed in Supplementary Section 2. Measurements are performed using a radiofrequency-calibrated interferometer in combination with a wavelength-tunable laser3. The coupled resonators feature two frequency bands in which three anomalous dispersion windows are highlighted. At each window, soliton steps are observed when scanning the laser frequency over a cavity resonance. Magnified views of the steps are presented as insets in Fig. 2b. Extended scans are provided in Extended Data Fig. 2 including appearance of the standard thermal triangle associated with photo-thermal heating of the resonator. Operation at the longest and shortest wavelength windows (1,584.5 nm and 1,525.5 nm) was challenging due to the low power of the laboratory laser, and as a result the time duration of the soliton steps for these wavelengths is relatively shorter.

Analysis shows that the average frequency of the two bands (that is, ωμ ≡ (ωμ,+ + ωμ,−)/2) is given by the mode frequency for a length-averaged resonator at the same mode number (see Supplementary Section 1). This average frequency can be described by a second-order dispersion model:

$${\omega }_{\mu }\approx {\omega }_{0}+{D}_{1}\mu +\frac{1}{2}{D}_{2}{\mu }^{2}$$
(1)

where ω0 is the mode frequency at μ = 0 and μ is a relative mode number referenced to the frequency degeneracy at 1,552.3 nm; D1 is the length-averaged FSR for the resonator at μ = 0; \({D}_{2}=-c{D}_{1}^{2}{\beta }_{2}/{n}_{{{{\rm{g}}}}}\) is the second-order dispersion parameter at μ = 0, with group velocity dispersion β2 and waveguide group index ng. Averaging the frequencies removes the effect of the coupling entirely, and the resulting average dispersion (orange points in Fig. 2b) closely matches a parabolic-shaped dispersion curve (orange curve).

The effect of the coupling is made clearer by plotting the mode frequencies relative to the averaged frequency (that is, relative mode frequency ωμ,± − ωμ), as shown in Fig. 2c. The relative mode frequencies of uncoupled rings appear as straight lines. Their positive and negative slopes result from removing a linear component of dispersion in this plot given by the average FSR, D1. The mode number walk-off causes the lines to vertically wrap at ±D1/2. As the length of ring B is 0.5% longer than ring A, frequency degeneracy of the rings occurs every 200 ring A modes (or every 201 ring B modes). The introduction of coupling opens gaps at frequency degeneracies, regardless of whether the absolute mode number is matched.

Analysis shows that the gap widths equal 2G ≡ gcoLcoD1/π, where G is the half-gap-width in Hertz, gco is the coupling strength per unit length and Lco is the effective coupler length. The full dispersion relation is (see Supplementary Section 1):

$${\omega }_{\mu ,\pm }={\omega }_{\mu }\pm \frac{{D}_{1}}{2\uppi }\arccos \left[\cos ({g}_{{{{\rm{co}}}}}{L}_{{{{\rm{co}}}}})\cos \left(2\uppi \epsilon \mu \right)\right]$$
(2)

where ϵ = (LB − LA)/(LB + LA) = (2M)−1 is the length contrast of the rings, and LA (LB) is the length of ring A (B). For the current design ϵ = 1/401, and the gap is modulated with respect to mode number with period ϵ−1 = 401 (corresponding to 8 THz in the spectrum). The small length contrast ϵ guarantees the wide spectral range of the anomalous dispersion window. Overall, there is very good agreement between the model and the measured data in Fig. 2b,c, and the fitting allows determination of key resonator parameters. The hybrid mode field distributions between two rings are studied in the Supplementary Section 1 and the fractional energy contribution from ring A (ηA is defined in Supplementary Section 1) is used to colour the hybrid modes in Fig. 2b,c.

As an aside, the spectral gap is smaller at larger mode numbers, which is attributed to the wavelength dependence of gco, as shorter wavelength results in stronger mode confinement, and hence smaller coupling with the adjacent waveguide. When combined with the original normal dispersion of each ring, the net dispersion for coupled system remains anomalous at around μ = 0 and 400 for the upper branch, and at around μ = −200 and 200 for the lower branch.

Aside from the observation of soliton steps (Fig. 2b), microcomb spectra measured around 1,550 nm for the through (ring A) and drop (ring B) ports are presented in Fig. 1b. The experimental set-up is provided in Extended Data Fig. 3. The microcomb was stabilized by measuring comb power from the through port and feeding back to the pump laser frequency, which controls the pump–cavity offset frequency18. The comb exhibits excellent stability (measurements of the comb spectra and repetition rate over 4 h of operation are provided in Extended Data Fig. 4). The theoretical pulse width of the comb spectra in the figure is estimated to be ~250 fs. Microcomb spectra measured at other pump–cavity offset frequencies, and using another device, are presented in Extended Data Fig. 5. Comb coherence and soliton pulse behaviour were confirmed in several ways. The radiofrequency spectrum of the soliton beatnote is presented in Fig. 1c. The soliton \({{{\mathcal{S}}}}\)- and \({{{\mathcal{C}}}}\)-resonances19,20 were also measured using a vector network analyser. Plots of their relative frequencies versus laser-cavity detuning are given in Extended Data Fig. 6. Finally, time-domain autocorrelation measurements are also given in the Extended Data Fig. 6. Multiple pulse pair comb states are discussed in the next section, and autocorrelation measurements for these comb states are also included in Extended Data Fig. 6.

Fig. 3: Temporal evolution of the soliton pulse pair in the two-ring coupled resonator.
figure 3

a, Top, an illustration of the time evolution of the soliton pair inside the two rings during one round trip time; bottom, snapshots of the pulses at different positions. In the non-coupled regions (I and IV), pulses accumulate positive chirp due to nonlinearity and normal dispersion of the waveguide. Pulse in ring A is leading in time at I due to shorter ring circumference. When the pulses enter the coupling region (II), the pulses exchange energy, which leads to relative position shifts as well as chirp compensation (III). The pulses exit the coupled region (IV) with position shifts and chirping compensated. b, Simulated pulse-pair properties are plotted versus pulse position in each ring during one round trip. The two rings are aligned at the coupling region centre, and the surplus length in ring B is omitted in the figure. The yellow shaded area represents the coupling region. The quantities are, from top to bottom, the pulse timing difference (pulse centre-to-centre), linear chirp, peak power and theoretical pulse width τ. The blue (red) lines represent simulation results for the pulse in ring A (B). The dashed lines are analytical results from a linear coupling model (see Methods), and are consistent with simulation results.

Full size image
Fig. 4: Observation of bipartite and tripartite multisoliton states in two- and three-coupled-ring microresonators.
figure 4

a,b, Through port optical spectra of bipartite two-soliton states with different relative soliton positions. The state in b is a two-soliton crystal state. The insets show relative position of the two solitons inside each microresonator. c,d, Through port optical spectra of tripartite two-soliton states where solitons feature different relative positions in c and d. The insets show the relative position of the two solitons inside each microresonator. e, Optical spectrum of a tripartite three-soliton state. The inset shows the relative position of the three solitons inside each microresonator. f, Optical spectrum of a tripartite four-soliton crystal. The inset shows the relative position of the four solitons inside each microresonator.

Full size image

Through and drop port spectra correspond to pulses in rings A and B, respectively, and show that these pulses are both different from each other and deviate from the conventional sech2 shape of Kerr solitons. The through-port spectrum is stronger (weaker) than the drop port at shorter (longer) wavelengths. This is a result of this system representing a new version of the Dirac soliton16 (Methods). In Fig. 1b, two strong dispersive waves are observed near 1,526 nm and 1,577 nm, where modes of the coupled resonator phase-match to the soliton comb. For comparison, the dispersion in the vicinity of the comb spectrum is overlaid in the figure. The dispersive waves broaden the soliton spectrum and provide higher power comb lines (1.5 μW on-chip power at shorter wavelength and 5.4 μW at longer wavelength), which is advantageous for application to optical frequency division21.

Pulse generation in the three-ring system is shown in Fig. 1d (see Supplementary Section 2 for the dispersion analysis). Figure 1e shows the soliton spectrum measured from the centre ring. The measured dispersion is also included in the figure. The pump laser wavelength is several nanometres away from the anomalous dispersion centre frequency and, as a result, the spectrum features only one dispersive wave at the shorter wavelength side. The radiofrequency spectrum of the soliton beatnote is presented in Fig. 1f, indicating good coherence. Autocorrelation measurements for this device are presented in Extended Data Fig. 6.

Pulse pairs and multipartite states

Both autocorrelation measurements (Extended Data Fig. 6) and simulations show that microcombs form as phase-locked pulse pairs, where the pulses have opposite phases. The pair viewpoint provides a powerful framework for visualization of mode locking that readily explains observable multiple pulse-pair states and higher-dimensional systems comprising multiple coupled cavities.

Simulations of pulse propagation in the two-ring system are presented in Fig. 3a. Here the ring FSRs and couplings are those of the experimental system studied in Fig. 2b,c, and excitation occurs for the mode μ = 0. As shown in Fig. 3b, each pulse undergoes shape, chirp and pulse width variations that repeat upon every round trip. Before entering the coupling region (point I in Fig. 3a), the chirp of both pulses has increased due to uncompensated Kerr nonlinearity from propagation in normal dispersion waveguides of each ring. Pulse chirp is indicated in the lower panel of Fig. 3a, where the colour represents instantaneous frequency. The pulse in ring B (red) also lags behind its counterpart in ring A (blue) due to the difference in ring lengths; however, upon entering the coupling region (point II), the ring B (A) pulse accelerates (decelerates) and becomes the leading (lagging) pulse when exiting the coupling region (point III). The chirp of both pulses decreases through the coupling region. Upon exiting the coupling region, the pulses propagate in their respective waveguides (point IV) where chirp increases as the pulses circle back through point I. Detailed numerical simulations (see Methods) are used to further explore and confirm the pulse pair evolution (see Fig. 3b and Supplementary Video 1).

This picture of pairwise round-trip compensation of normal dispersion explains how compensation works for multipair systems, as well as for higher dimensions with additional ring cavities. Specifically, it constrains how comb states form. Consider the coupled-ring states in Fig. 4a,b, for example, wherein two pulse pairs circulate in a mirror-image-like fashion to form the observed spectra. Here, to reduce confusion with corresponding multipulse soliton systems, we adopt the nomenclature that a single pulse pair in a two-ring system is a bipartite single soliton (see Fig. 1a,b), whereas multipair states in a two-ring system are bipartite multisoliton systems. Accordingly, the states in Fig. 4a,b are bipartite two-soliton states. The state in Fig. 4b is moreover a bipartite two-soliton crystal. Autocorrelation characterization for this bipartite crystal state is presented in Extended Data Fig. 6 for comparison to single pulse pair state in the same figure. Notice that the requirements imposed on pulse pairing allow a one-to-one correspondence between conventional multisoliton states and bipartite states, since the pulse configurations in each ring resonator mirror those of the neighbouring ring.

The same is true for higher-dimensional systems. For example, three pulses compensate normal dispersion by alternating their pairwise coupling (Fig. 1d). Moreover, the pairwise compensation works when additional pulses are added to each cavity. For example, measurement of tripartite two- and three-soliton states, and a four-soliton crystal state (containing 6, 9 and 12 pulses, respectively) are presented in Fig. 4c–f. Notice that the measured comb line spacing (79.93 GHz) for the crystal state is four times the FSR of a single ring as is consistent with a conventional four-soliton crystal state. Backscattering inside the cavity and coupling to the external waveguide might contribute to this self-organization behaviour.

Discussion

In summary, we have observed a new type of microcavity soliton that mode locks as pulse pairs distributed spatially over multiple ring resonators. The requirement to compensate overall normal dispersion of the rings requires that the pulses in each ring arrange themselves as a mirror image of the pulses in neighbouring rings. Partial coupling of the resonators creates a situation in which the ring resonator mode number is not conserved and this enables recurring spectral windows in which the pairs can be formed. The presented bright soliton results use the ultra-low-loss silicon nitride process that has previously been restricted to only dark pulse generation. This methodology can be generalized to other material platforms.

Critically, the combination of pulsed parametric oscillation and ultra-low optical loss in a fully complementary metal oxide semiconductor (CMOS) compatible platform brings a high level of integration complexity to many applications. More complex, optical-frequency-division systems and spectroscopy systems are possible using these short pulse combs. Comb dividers could also use the strong dispersive waves in the soliton spectrum, when locked to a cavity reference, to produce low-noise radio frequency signals. Meanwhile, high-Q factor in this platform will benefit quantum comb applications22,23,24 including squeezed quantum combs25,26. Here, the full CMOS compatibility and ultra-low-loss waveguides can readily facilitate chip integration of delay line and beam splitter functions that have been applied recently to create large cluster states by time domain multiplexing and entanglement27,28. It is also worth noting that the pulse pair systems demonstrated here exist across multiple coupled rings, suggesting connections to topological photonics29,30,31. Theoretical studies of topological phenomena in coupled-ring parametric oscillators showcase the range of intriguing phenomena that are possible32. Finally, the ability to distribute coherent pulses over multiple rings with individual taps and with simultaneous pulse formation at multiple wavelengths presents new opportunities for soliton science and microcomb applications, including new realizations optical buffers as originally proposed for coherently pumped solitons33,34. As an aside, a study of the zero GVD dispersion regime in this coupled resonator system is reported in ref. 35.

Methods

Resonator design

The rings consist of Si3N4 waveguides (2,800 nm width and 100 nm thickness) embedded in silica and formed into a racetrack shape. The waveguide cross-section only supports one polarization mode. Detailed information on fabrication steps can be found in ref. 4. For the two-ring device, ring A has a circumference of 9.5 mm, and ring B is 0.5% longer. For the three-ring device, the right-most ring has a circumference of 9.5 mm, and each other ring is 0.3% longer than its neighbour to the right. The adiabatic waveguide bend has the shape of a fifth-degree spline such that the curvature is continuous along the curve and transition loss is minimized. The gap between the inner edges of the two waveguides in the coupling region is 2,400 nm, and the effective coupling length is 1.0 mm including contributions from the adiabatic bend (which is 10.5% of the shortest ring circumference).

The simulated dispersion of straight Si3N4 waveguides with 2.8 μm width are shown in Extended Data Fig. 1a. For these calculations, the effective index of the fundamental TE mode was calculated and the group velocity dispersion determined through β2 = λ3/(2πc2)∂2nwg/∂λ2, where λ is the vacuum wavelength. For waveguides with thicknesses under 780 nm, the fundamental TE mode always features normal dispersion in the C-band. To maintain high optical Q factors, the waveguide thickness is about 100 nm for the current process, which places the waveguide deep into the normal dispersion region.

Simulations of the waveguide coupling rate gco with 2.4 μm coupling gap are presented in Extended Data Fig. 1b. The effective index of the two supermodes at the coupling region is calculated, and the coupling rate gco is related to the index difference of the supermodes Δnwg by gco = Δnwgπ/λ. With a thinner waveguide or a longer wavelength, the optical confinement is weaker, leading to a larger coupling strength and larger spectral gap width.

Dispersion measurement and fitting

The dispersion is measured by sweeping a mode-hop-free laser while pumping the resonator, recording the mode positions from the transmission signal, and comparing it against a calibrated Mach–Zehnder interferometer3. The averaged mode frequencies are fitted by a second-order dispersion model given by equation (1) with D1 = 2π × 19.9766 GHz and D2 = 2π × (−283.0) kHz. The relative frequencies are fitted with equation (2), where we assume that the coupling is exponentially decaying with respect to mode number:

$${g}_{{{{\rm{co}}}}}={g}_{{{{\rm{co,0}}}}}\exp (-\mu /{\mu }_{g})$$
(3)

where μg gives a decay scale. The fitting uses gco,0, μg and the crossing centre position as fitting parameters, whereas D1 and D2 are derived from the mode frequency average fitting and ϵ = 1/401 is taken from design values. Fitting gives gco,0Lco = 0.954 and μg = 1,196. The coupling is equivalent to a 33:67% coupler near μ = 0, and the coupling rate increases by 5.4% for every 10 nm increased near 1,550 nm. The coupling rate and decaying scale are close to simulation results (gco,0Lco = 0.782, 5.5% increase per 10 nm; see Extended Data Fig. 1b). Differences between measured and simulated values may result from variations to the refractive index and layer thickness.

Dynamics of the soliton pulse pair

The optical fields in the two rings are governed by the coupled nonlinear wave equations:

$$\begin{array}{lll}\frac{\partial {E}_{{{{\rm{A}}}}}}{\partial t}&=&-\left(\frac{\kappa }{2}+i\delta {\omega }_{{{{\rm{A}}}}}\right){E}_{{{{\rm{A}}}}}-{v}_{{{{\rm{g}}}}}\frac{\partial {E}_{{{{\rm{A}}}}}}{\partial z}-i\frac{{\beta }_{2}{v}_{{{{\rm{g}}}}}^{3}}{2}\frac{{\partial }^{2}{E}_{{{{\rm{A}}}}}}{\partial {z}^{2}}\\ &&+i{g}_{{{{\rm{co}}}}}{v}_{{{{\rm{g}}}}}{\chi }_{{{{\rm{co}}}}}(z){E}_{{{{\rm{B}}}}}+i{g}_{{{{\rm{NL}}}}}| {E}_{{{{\rm{A}}}}}{| }^{2}{E}_{{{{\rm{A}}}}}+F\end{array}$$
(4)
$$\begin{array}{lll}\frac{\partial {E}_{{{{\rm{B}}}}}}{\partial t}&=&-\left(\frac{\kappa }{2}+i\delta {\omega }_{{{{\rm{B}}}}}\right){E}_{{{{\rm{B}}}}}-{v}_{{{{\rm{g}}}}}\frac{\partial {E}_{{{{\rm{B}}}}}}{\partial z}-i\frac{{\beta }_{2}{v}_{{{{\rm{g}}}}}^{3}}{2}\frac{{\partial }^{2}{E}_{{{{\rm{B}}}}}}{\partial {z}^{2}}\\ &&+i{g}_{{{{\rm{co}}}}}{v}_{{{{\rm{g}}}}}{\chi }_{{{{\rm{co}}}}}(z){E}_{{{{\rm{A}}}}}+i{g}_{{{{\rm{NL}}}}}| {E}_{{{{\rm{B}}}}}{| }^{2}{E}_{{{{\rm{B}}}}}\end{array}$$
(5)

accompanied by periodic boundary conditions in the z-direction, where EA,B denotes the optical field in the two rings normalized to photon numbers in the corresponding length-averaged ring; κ = κin + κex is the loss rate (sum of intrinsic and external loss) for the individual rings (assumed to be identical for rings A and B), which can be linked to the quality factors via κ = ω0/Q, κin = ω0/Qin, and κex = ω0/Qex. Furthermore, δωA,B = ω0A,B − ωp is the pump laser detuning; vg = c/ng is the group velocity of the waveguide; z ∈ [0, LA,B) is the resonator coordinate, with LA,B the ring length; β2 is the waveguide group velocity dispersion; gco is the coupling strength between the two waveguides in the coupling region; χco(z) is the indicator function, with value 1 in the coupling region and 0 elsewhere; \({g}_{{{{\rm{NL}}}}}=\hslash {\omega }_{0}^{2}{D}_{1}{n}_{2}/(2\uppi {n}_{{{{\rm{g}}}}}{A}_{{{{\rm{eff}}}}})\) is the nonlinear coefficient, with Aeff being the effective mode area; and \(F=\sqrt{{\kappa }_{{{{\rm{ex}}}}}{P}_{{{{\rm{in}}}}}/\hslash {\omega }_{0}}\) is the pump term, where Pin is the on-chip pump power. For simplicity, the pump and loss terms are averaged over the entire resonator without considering the detailed coupling geometry between the rings and the bus waveguides, and the coupling is assumed to be wavelength independent (gco = gco,0). A similar coupled equation set holds for the three-coupled-ring device.

Numerical simulations have been performed based on the above nonlinear wave equations. For the evolution of intracavity waveforms, we use the fourth-order Runge–Kutta method to update the fields in slow time t, in which a discrete Fourier-transformation is used to calculate the fast time derivative terms (with respect to the resonator coordinate, z). The results are used to plot Fig. 3b and compare with the optical spectra in Fig. 1b,e (see Extended Data Fig. 7). Parameters used for numerical simulations are: ω0 = 2π × 193.34 THz; Qin = 75 × 106; Qex = 45 × 106; δωA = δωB = 10κ − G, where G is the half gap created by the coupling (pump is red-detuned with respect to the upper branch resonance by 10κ); D1 = 2π × 19.9766 GHz; D2 = −2π × 283.0 kHz; ng = 1.575; Pin = 200 mW; gNL = 0.0277 s−1 and gco,0 = 0.954 mm−1.

Resemblance to Dirac solitons

To demonstrate that the resulting soliton resembles the optical Dirac soliton16, we will convert the nonlinear wave equations (equations (4) and (5)) into a form that is analogous to the Dirac equation in quantum field theory. We start by defining a common round trip variable θ for both resonators, with θ = 2πz/LA for ring A and θ = 2πz/LB for ring B. With this change, the coupled equations read

$$\begin{array}{lll}\frac{\partial {E}_{{{{\rm{A}}}}}}{\partial t}&=&-\left(\frac{\kappa }{2}+i\delta {\omega }_{{{{\rm{A}}}}}\right){E}_{{{{\rm{A}}}}}\\ &&-\frac{{D}_{1}}{1-\epsilon }\frac{\partial {E}_{{{{\rm{A}}}}}}{\partial \theta }+i\frac{{D}_{2}}{2{(1-\epsilon )}^{2}}\frac{{\partial }^{2}{E}_{{{{\rm{A}}}}}}{\partial {\theta }^{2}}\\ &&+i{g}_{{{{\rm{co}}}}}{v}_{{{{\rm{g}}}}}{\chi }_{{{{\rm{co}}}}}(\theta ){E}_{{{{\rm{B}}}}}+i{g}_{{{{\rm{NL}}}}}| {E}_{{{{\rm{A}}}}}{| }^{2}{E}_{{{{\rm{A}}}}}+F\end{array}$$
(6)

and similarly for EB with ϵ replaced by −ϵ and pump term dropped. The unified round trip variable breaks the correspondence of waveguide sections in the coupling region, but these have been neglected as the pulse width is much larger compared to the waveguide coordinate difference (corresponding to 10.5% of the ring length difference; see Fig. 3b). Switching to the co-moving frame of the pulse [ψA,B(θ, t) ≡ EA,B(θ + D1t, t)] leads to

$$\begin{array}{lll}\frac{\partial {\psi }_{{{{\rm{A}}}}}}{\partial t}&\approx &-\left(\frac{\kappa }{2}+i\delta {\omega }_{{{{\rm{A}}}}}\right){\psi }_{{{{\rm{A}}}}}-\epsilon {D}_{1}\frac{\partial {\psi }_{{{{\rm{A}}}}}}{\partial \theta }+i\frac{{D}_{2}}{2}\frac{{\partial }^{2}{\psi }_{{{{\rm{A}}}}}}{\partial {\theta }^{2}}\\ &&+iG{\psi }_{{{{\rm{B}}}}}+i{g}_{{{{\rm{NL}}}}}| {\psi }_{{{{\rm{A}}}}}{| }^{2}{\psi }_{{{{\rm{A}}}}}+F\end{array}$$
(7)

and similarly for EB, where we retain the lowest order of ϵ and further assume that the pulse varies slowly within one round trip such that the effect of coupling is averaged over the resonator length (equivalent to uniform coupling which conserves the mode number). Finally, shifting the wavevector and frequency reference (\({\tilde{\psi }}_{{{{\rm{A,B}}}}}\equiv {\psi }_{{{{\rm{A,B}}}}}\exp (i{k}_{0}\theta -i{\omega }_{0}t)\)) gives

$$\begin{array}{lll}\frac{\partial {\tilde{\psi }}_{{{{\rm{A}}}}}}{\partial t}&\approx &-i\left(\delta {\omega }_{{{{\rm{A}}}}}-\epsilon {D}_{1}{k}_{0}+{\omega }_{0}\right){\tilde{\psi }}_{{{{\rm{A}}}}}-\epsilon {D}_{1}\frac{\partial {\tilde{\psi }}_{{{{\rm{A}}}}}}{\partial \theta }+iG{\tilde{\psi }}_{{{{\rm{B}}}}}\\ &&+i{g}_{{{{\rm{NL}}}}}| {\tilde{\psi }}_{{{{\rm{A}}}}}{| }^{2}{\tilde{\psi }}_{{{{\rm{A}}}}}\\ &&-\frac{\kappa }{2}{\tilde{\psi }}_{{{{\rm{A}}}}}+i\frac{{D}_{2}}{2}\frac{{\partial }^{2}{\tilde{\psi }}_{{{{\rm{A}}}}}}{\partial {\theta }^{2}}+F\exp (i{k}_{0}\theta -i{\omega }_{0}t)\\ \end{array}$$
(8)
$$\begin{array}{lll}\frac{\partial {\tilde{\psi }}_{{{{\rm{B}}}}}}{\partial t}&\approx &-i\left(\delta {\omega }_{{{{\rm{B}}}}}+\epsilon {D}_{1}{k}_{0}+{\omega }_{0}\right){\tilde{\psi }}_{{{{\rm{B}}}}}+\epsilon {D}_{1}\frac{\partial {\tilde{\psi }}_{{{{\rm{B}}}}}}{\partial \theta }+iG{\tilde{\psi }}_{{{{\rm{A}}}}}\\ &&+i{g}_{{{{\rm{NL}}}}}| {\tilde{\psi }}_{{{{\rm{B}}}}}{| }^{2}{\tilde{\psi }}_{{{{\rm{B}}}}}\\ &&-\frac{\kappa }{2}{\tilde{\psi }}_{{{{\rm{B}}}}}+i\frac{{D}_{2}}{2}\frac{{\partial }^{2}{\tilde{\psi }}_{{{{\rm{B}}}}}}{\partial {\theta }^{2}}\end{array}$$
(9)

where we assume that we are pumping near the crossing centre such that ϵD1 ≪ D2k0 and high-order terms in k0 could be neglected. Choosing k0 = (δωA − δωB)/(2ϵD1) and ω0 = − (δωA + δωB)/2 removes the effective detuning terms from the two equations.

This can now be compared with the massive Dirac equation in 1 + 1 dimension written in a chiral basis36:

$${\partial }_{t}{\psi }_{{{{\rm{L}}}}}=-c{\partial }_{x}{\psi }_{{{{\rm{L}}}}}+i\frac{M{c}^{2}}{\hslash }{\psi }_{{{{\rm{R}}}}}$$
(10)
$${\partial }_{t}{\psi }_{{{{\rm{R}}}}}=+c{\partial }_{x}{\psi }_{{{{\rm{R}}}}}+i\frac{M{c}^{2}}{\hslash }{\psi }_{{{{\rm{L}}}}}$$
(11)

where M is interpreted as the mass, and corresponds to the coupling term (the massless Dirac equation with M = 0 would correspond to an uncoupled system with the frequency gap closed). The momentum term corresponds to the FSR difference. The nonlinear term converts the equation into a nonlinear Dirac equation, although there is no exact analogue of the self-phase modulation in quantum field theory as this contradicts the Pauli exclusion principle. Loss, pump and second-order dispersion terms do not have analogues in the nonlinear Dirac equation, and could be treated as perturbations for the soliton dynamics. For example, D2 is no longer the dominant contribution to dispersion near the mode crossing centre. We note that these terms do not change the qualitative feature of the generated soliton, therefore establishing the link between the current soliton and the optical Dirac soliton previously studied16. A comparison of the simulated soliton profile using different levels of approximations can be found in Extended Data Fig. 8.

Dirac soliton dynamics in the coupling region

In the coupling region where linear interaction is dominant in the Dirac soliton dynamics, the coupled nonlinear wave equations can be reduced to:

$$\frac{\partial {E}_{{{{\rm{A}}}}}}{\partial z}+\frac{1}{{v}_{{{{\rm{g}}}}}}\frac{\partial {E}_{{{{\rm{A}}}}}}{\partial t}=i{g}_{{{{\rm{co}}}}}{E}_{{{{\rm{B}}}}}$$
(12)
$$\frac{\partial {E}_{{{{\rm{B}}}}}}{\partial z}+\frac{1}{{v}_{{{{\rm{g}}}}}}\frac{\partial {E}_{{{{\rm{B}}}}}}{\partial t}=i{g}_{{{{\rm{co}}}}}{E}_{{{{\rm{A}}}}},$$
(13)

where z = 0 denotes the beginning of the coupling region. Note that gco here is assumed to be wavelength independent for simplicity. The optical fields at z can be related to the incident fields (z = 0) as

$${E}_{{{{\rm{A}}}}}(z,t)=\cos ({g}_{{{{\rm{co}}}}}z){E}_{{{{\rm{A}}}}}(0,{t}^{{\prime} })+i\sin ({g}_{{{{\rm{co}}}}}z){E}_{{{{\rm{B}}}}}(0,{t}^{{\prime} })$$
(14)
$${E}_{{{{\rm{B}}}}}(z,t)=\cos ({g}_{{{{\rm{co}}}}}z){E}_{{{{\rm{B}}}}}(0,{t}^{{\prime} })+i\sin ({g}_{{{{\rm{co}}}}}z){E}_{{{{\rm{A}}}}}(0,{t}^{{\prime} })$$
(15)

where \({t}^{{\prime} }=t-z/{v}_{{{{\rm{g}}}}}\) is the retarded time. The evolution of soliton properties with propagation distance plotted in Fig. 2c is obtained from equations (14) and (15), with initial conditions \({E}_{{{{\rm{A,B}}}}}(0,{t}^{{\prime} })\) taken from simulations, and shows good agreement with the simulation results using equations (4) and (5).