Abstract
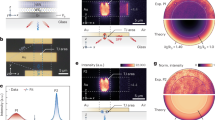
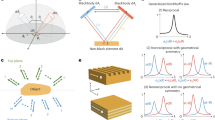
Conventional laser cavities require discontinuity of material property or disorder to localize a light field for feedback. Recently, an emerging class of materials, twisted van der Waals materials, have been explored for applications in electronics and photonics. Here we propose and develop magic-angle lasers, where the localization is realized in periodic twisted photonic graphene superlattices. We reveal that the confinement mechanism of magic-angle lasers does not rely on a full bandgap but on the mode coupling between two twisted layers of photonic graphene lattice. Without any fine-tuning in structure parameters, a simple twist can result in nanocavities with strong field confinement and a high quality factor. Furthermore, the emissions of magic-angle lasers allow direct imaging of the wavefunctions of magic-angle states. Our work provides a robust platform to construct high-quality nanocavities for nanolasers, nano light-emitting diodes, nonlinear optics and cavity quantum electrodynamics at the nanoscale.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The authors declare that the main data supporting the findings of this study are available within the article and its Supplementary Information. Extra data are available from the corresponding author upon reasonable request.
References
Geim, A. & Grigorieva, I. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Liu, Y. et al. Van der Waals heterostructures and devices. Nat. Rev. Mater. 1, 16042 (2016).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 461, aac9439 (2016).
Lopes dos Santos, J. L., Peres, N. M. R. & Castro Neto, A. C. Graphene bilayer with a twist: electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Suárez Morell, E., Correa, J. D., Vargas, P., Pacheco, M. & Barticevic, Z. Flat bands in slightly twisted bilayer graphene: tight-binding calculations. Phys. Rev. B 82, 121407(R) (2010).
Li, G. et al. Observation of Van Hove singularities in twisted graphene layers. Nat. Phys. 6, 109–113 (2010).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Carr, S. et al. Twistronics: manipulating the electronic properties of two-dimensional layered structures through their twist angle. Phys. Rev. B 95, 075420 (2017).
Kim, K. et al. Tunable moiré bands and strong correlations in small-twist-angle bilayer graphene. Proc. Natl Acad. Sci. USA 114, 3364–3369 (2017).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Ribeiro-Palau, R. et al. Twistable electronics with dynamically rotatable heterostructures. Science 361, 690–693 (2018).
Alexeev, E. M. et al. Resonantly hybridized excitons in moiré superlattices in van der Waals heterostructures. Nature 567, 81–86 (2019).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Jin, C. et al. Observation of moiré excitons in WSe2/WS2 heterostructure superlattices. Nature 567, 76–80 (2019).
Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).
Ciarrocchi, A. et al. Polarization switching and electrical control of interlayer excitons in two-dimensional van der Waals heterostructures. Nat. Photon. 13, 131–136 (2019).
Shimazaki, Y. et al. Strongly correlated electrons and hybrid excitons in a moiré heterostructure. Nature 580, 472–477 (2020).
Brotons-Gisbert, M. A. et al. Spin–layer locking of interlayer excitons trapped in moiré potentials. Nat. Mater. 19, 630–636 (2020).
Li, W. et al. Dipolar interactions between localized interlayer excitons in van der Waals heterostructures. Nat. Mater. 19, 624–629 (2020).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Kennes, D. M. et al. Moiré heterostructures as a condensed-matter quantum simulator. Nat. Phys. 17, 155–163 (2021).
MacDonald, A. H. Trend: bilayer graphene’s wicked, twisted road. Physics 12, 12 (2019).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019).
Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).
Sunku, S. S. et al. Photonic crystals for nano-light in moiré graphene superlattices. Science 362, 1153–1156 (2018).
Wang, P. et al. Localization and delocalization of light in photonic moiré lattices. Nature 577, 42–46 (2020).
Lassaline, N. et al. Optical Fourier surfaces. Nature 582, 506–510 (2020).
Fu, Q. et al. Optical soliton formation controlled by angle twisting in photonic moiré lattices. Nat. Photon. 14, 663–668 (2020).
Wang, W. et al. Moiré fringe induced gauge field in photonics. Phys. Rev. Lett. 125, 203901 (2020).
Hu, G. et al. Moiré hyperbolic metasurfaces. Nano Lett. 20, 3217–3224 (2020).
Hu, G. et al. Topological polaritons and photonic magic angles in twisted α-MoO3 bilayers. Nature 582, 209–213 (2020).
Chen, M. et al. Configurable phonon polaritons in twisted α-MoO3. Nat. Mater. 19, 1307–1311 (2020).
Duan, J. et al. Twisted nano-optics: manipulating light at the nanoscale with twisted phonon polaritonic slabs. Nano Lett. 20, 5323–5329 (2020).
Zheng, Z. et al. Phonon polaritons in twisted double-layers of hyperbolic van der Waals crystals. Nano Lett. 20, 5301–5308 (2020).
Vahala, K. J. Optical microcavities. Nature 424, 839–846 (2003).
Ma, R. M. & Oulton, R. F. Applications of nanolasers. Nat. Nanotechnol. 14, 12–22 (2019).
Carr, S., Fang, S., Jarillo-Herrero, P. & Kaxiras, E. Pressure dependence of the magic twist angle in graphene superlattices. Phys. Rev. B 98, 085144 (2018).
Yankowitz, M. et al. Dynamic band-structure tuning of graphene moiré superlattices with pressure. Nature 557, 404–408 (2018).
Björk, G., Karlsson, A. & Yamamoto, Y. Definition of a laser threshold. Phys. Rev. A 50, 1675–1680 (1994).
Ma, R. M. Lasing under ultralow pumping. Nat. Mater. 18, 1152–1153 (2019).
Painter, O. et al. Two-dimensional photonic band-gap defect mode laser. Science 284, 1819–1821 (1999).
Asano, T. & Noda, S. Photonic crystal devices in silicon photonics. Proc. IEEE 106, 2183–2195 (2018).
Tsakmakidis, K. L., Hess, O., Boyd, R. W. & Zhang, X. Ultraslow waves on the nanoscale. Science 358, eaan5196 (2017).
DeGiorgio, V. & Scully, M. O. Analogy between the laser threshold region and a second-order phase transition. Phys. Rev. A 2, 1170–1177 (1970).
Haken, H. in Synergetics (eds. Pacault, A. & Vidal, C.) 22–33 (Springer, 1979).
Tsakmakidis, K. L., Jha, P. K., Wang, Y. & Zhang, X. Quantum coherence-driven self-organized criticality and nonequilibrium light localization. Sci. Adv. 4, eaaq0465 (2018).
Acknowledgements
This work is supported by the Beijing Natural Science Foundation (grant no. Z180011), the National Natural Science Foundation of China (grant nos. 91950115, 11774014 and 61521004) and the National Key R&D Program of China (grant no. 2018YFA0704401).
Author information
Authors and Affiliations
Contributions
R.-M.M. conceived and supervised the project. X.-R.M., Z.-K.S. and R.-M.M. performed the optical characterization. Z.-K.S. fabricated the devices. H.-Y.L. and S.-L.W. carried out the numerical simulations. R.-M.M., X.-R.M. and H.-Y.L. did the data analysis. R.-M.M. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Nanotechnology thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Sections 1–15 and Figs. 1–24.
Rights and permissions
About this article
Cite this article
Mao, XR., Shao, ZK., Luan, HY. et al. Magic-angle lasers in nanostructured moiré superlattice. Nat. Nanotechnol. 16, 1099–1105 (2021). https://doi.org/10.1038/s41565-021-00956-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-021-00956-7
This article is cited by
-
Realization of all-band-flat photonic lattices
Nature Communications (2024)
-
Twisted photonic Weyl meta-crystals and aperiodic Fermi arc scattering
Nature Communications (2024)
-
Inorganic perovskite-based active multifunctional integrated photonic devices
Nature Communications (2024)
-
Observation of localization of light in linear photonic quasicrystals with diverse rotational symmetries
Nature Photonics (2024)
-
Two-dimensional localized modes in nonlinear systems with linear nonlocality and moiré lattices
Frontiers of Physics (2024)