Abstract
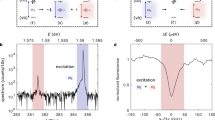
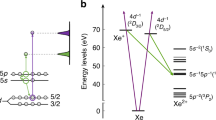
In a multi-electron atom, an excited electron can decay by emitting a photon. Typically, the leftover electrons are in their ground state. In a radiative Auger process, the leftover electrons are in an excited state and a redshifted photon is created1,2,3,4. In a semiconductor quantum dot, radiative Auger is predicted for charged excitons5. Here we report the observation of radiative Auger on trions in single quantum dots. For a trion, a photon is created on electron–hole recombination, leaving behind a single electron. The radiative Auger process promotes this additional (Auger) electron to a higher shell of the quantum dot. We show that the radiative Auger effect is a powerful probe of this single electron: the energy separations between the resonance fluorescence and the radiative Auger emission directly measure the single-particle splittings of the electronic states in the quantum dot with high precision. In semiconductors, these single-particle splittings are otherwise hard to access by optical means as particles are excited typically in pairs, as excitons. After the radiative Auger emission, the Auger carrier relaxes back to the lowest shell. Going beyond the original theoretical proposals, we show how applying quantum optics techniques to the radiative Auger photons gives access to the single-electron dynamics, notably relaxation and tunnelling. This is also hard to access by optical means: even for quasi-resonant p-shell excitation, electron relaxation takes place in the presence of a hole, complicating the relaxation dynamics. The radiative Auger effect can be exploited in other semiconductor nanostructures and quantum emitters in the solid state to determine the energy levels and the dynamics of a single carrier.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support this work are available from the corresponding author upon reasonable request.
Code availability
The code that has been used for this work is available from the corresponding author upon reasonable request.
References
Åberg, T. & Utriainen, J. Evidence for a ‘radiative Auger effect’ in X-ray photon emission. Phys. Rev. Lett. 22, 1346–1348 (1969).
Åberg, T. Theory of the radiative Auger effect. Phys. Rev. A 4, 1735–1740 (1971).
Bloch, F. & Ross, P. A. Radiative Auger effect. Phys. Rev. 47, 884–885 (1935).
Bloch, F. Double electron transitions in X-ray spectra. Phys. Rev. 48, 187 (1935).
Hawrylak, P. Single Quantum Dots: Fundamentals, Applications and New Concepts Vol. 90 (Springer Science, Business Media, 2003).
Bambynek, W. et al. X-ray fluorescence yields, Auger, and Coster–Kronig transition probabilities. Rev. Mod. Phys. 44, 716–813 (1972).
Barthés-Labrousse, M.-G. The Auger effect. Microsc. Microanal. Microstruct. 6, 253–262 (1995).
Kurzmann, A., Ludwig, A., Wieck, A. D., Lorke, A. & Geller, M. Auger recombination in self-assembled quantum dots: quenching and broadening of the charged exciton transition. Nano Lett. 16, 3367–3372 (2016).
Han, B. et al. Exciton states in monolayer MoSe2 and MoTe2 probed by upconversion spectroscopy. Phys. Rev. X 8, 031073 (2018).
Siyushev, P. et al. Optically controlled switching of the charge state of a single nitrogen-vacancy center in diamond at cryogenic temperatures. Phys. Rev. Lett. 110, 167402 (2013).
Blood, P. Quantum Confined Laser Devices: Optical Gain and Recombination in Semiconductors Vol. 23 (OUP Oxford, 2015).
Carlson, T. A. Electron shake-off following the beta decay of Ne23. Phys. Rev. 130, 2361–2365 (1963).
Dean, P. J., Cuthbert, J. D., Thomas, D. G. & Lynch, R. T. Two-electron transitions in the luminescence of excitons bound to neutral donors in gallium phosphide. Phys. Rev. Lett. 18, 122–124 (1967).
Skolnick, M. S. et al. Fermi sea shake-up in quantum well luminescence spectra. Solid State Electron. 37, 825–829 (1994).
Manfra, M. J., Goldberg, B. B., Pfeiffer, L. & West, K. Anderson–Fano resonance and shake-up processes in the magnetophotoluminescence of a two-dimensional electron system. Phys. Rev. B 57, R9467–R9470 (1998).
Kleemans, N. A. J. M. et al. Many-body exciton states in self-assembled quantum dots coupled to a Fermi sea. Nat. Phys. 6, 534–538 (2010).
Huo, Y. H., Rastelli, A. & Schmidt, O. G. Ultra-small excitonic fine structure splitting in highly symmetric quantum dots on GaAs (001) substrate. Appl. Phys. Lett. 102, 152105 (2013).
Warburton, R. J. et al. Optical emission from a charge-tunable quantum ring. Nature 405, 926–929 (2000).
Hansom, J., Schulte, C. H. H., Matthiesen, C., Stanley, M. J. & Atatüre, M. Frequency stabilization of the zero-phonon line of a quantum dot via phonon-assisted active feedback. Appl. Phys. Lett. 105, 172107 (2014).
Koong, Z. X. et al. Fundamental limits to coherent photon generation with solid-state atom-like transitions. Phys. Rev. Lett. 123, 167402 (2019).
Brash, A. J. et al. Light scattering from solid-state quantum emitters: beyond the atomic picture. Phys. Rev. Lett. 123, 167403 (2019).
Kouwenhoven, L. P., Austing, D. G. & Tarucha, S. Few-electron quantum dots. Rep. Prog. Phys. 64, 701–736 (2001).
Fock, V. Bemerkung zur Quantelung des harmonischen Oszillators im Magnetfeld. Z. Phys. 47, 446–448 (1928).
Darwin, C. G. The diamagnetism of the free electron. Proc. Camb. Phil. Soc. 27, 86 (1930).
Ohnesorge, B., Albrecht, M., Oshinowo, J., Forchel, A. & Arakawa, Y. Rapid carrier relaxation in self-assembled Inx Ga1−x As/GaAs quantum dots. Phys. Rev. B 54, 11532–11538 (1996).
Kurtze, H. et al. Carrier relaxation dynamics in self-assembled semiconductor quantum dots. Phys. Rev. B 80, 235319 (2009).
Li, X.-Q., Nakayama, H. & Arakawa, Y. Phonon bottleneck in quantum dots: role of lifetime of the confined optical phonons. Phys. Rev. B 59, 5069–5073 (1999).
Müller, K. et al. Probing ultrafast carrier tunneling dynamics in individual quantum dots and molecules. Ann. Phys. 525, 49–58 (2013).
Slater, J. C. The theory of complex spectra. Phys. Rev. 34, 1293–1322 (1929).
Bethe, H. A. & Jackiw, R. Intermediate Quantum Mechanics (CRC Press, 2018).
Löbl, M. C. et al. Narrow optical linewidths and spin pumping on charge-tunable close-to-surface self-assembled quantum dots in an ultrathin diode. Phys. Rev. B 96, 165440 (2017).
Vora, P. M. et al. Spin-cavity interactions between a quantum dot molecule and a photonic crystal cavity. Nat. Commun. 6, 7665 (2015).
Javadi, A. et al. Spin-photon interface and spin-controlled photon switching in a nanobeam waveguide. Nat. Nanotechnol. 13, 398–403 (2018).
Grim, J. Q. et al. Scalable in operando strain tuning in nanophotonic waveguides enabling three-quantum-dot superradiance. Nat. Mater. 18, 963–969 (2019).
Wang, Z. M., Liang, B. L., Sablon, K. A. & Salamo, G. J. Nanoholes fabricated by self-assembled gallium nanodrill on GaAs(100). Appl. Phys. Lett. 90, 113120 (2007).
Patel, R. B. et al. Two-photon interference of the emission from electrically tunable remote quantum dots. Nat. Photon. 4, 632–635 (2010).
Kiršanskė, G. et al. Indistinguishable and efficient single photons from a quantum dot in a planar nanobeam waveguide. Phys. Rev. B 96, 165306 (2017).
Kroutvar, M. et al. Optically programmable electron spin memory using semiconductor quantum dots. Nature 432, 81–84 (2004).
Dreiser, J. et al. Optical investigations of quantum dot spin dynamics as a function of external electric and magnetic fields. Phys. Rev. B 77, 075317 (2008).
Smith, J. M. et al. Voltage control of the spin dynamics of an exciton in a semiconductor quantum dot. Phys. Rev. Lett. 94, 197402 (2005).
Acknowledgements
We thank P. Treutlein for fruitful discussions. M.C.L., C.S. and R.J.W. acknowledge financial support from NCCR QSIT and from SNF project number 200020_156637. L.Z. received funding from the European Union Horizon 2020 Research and Innovation programme under the Marie Skłodowska-Curie grant agreement number 721394 (4PHOTON). A.J. acknowledges support from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement number 840453 (HiFig). J.R., A.L. and A.D.W. gratefully acknowledge financial support from the grants DFH/UFA CDFA05-06, DFG TRR160, DFG project 383065199, and BMBF Q.Link.X 16KIS0867. L.M. and P.L. gratefully acknowledge financial support from the Danish National Research Foundation (Center of Excellence Hy-Q, grant number DNRF139) and the European Research Council (ERC Advanced Grant SCALE).
Author information
Authors and Affiliations
Contributions
M.C.L., C.S., L.Z., G.N.N. and A.J. performed the experiments. J.R., A.D.W. and A.L. grew the samples. C.S., M.C.L. and L.M. fabricated the different samples. M.C.L., L.Z., P.L. and A.L. designed the samples. M.C.L., C.S., L.Z. and R.J.W. analysed the data. M.C.L. developed the theory of the radiative Auger process. A.J., M.C.L. and C.S. developed the theory for the time-resolved measurements. M.C.L., R.J.W. and C.S. developed the theory for the magnetic field dispersion. M.C.L. and R.J.W. initiated the project and wrote the manuscript with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Nanotechnology thanks Val Zwiller and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–6, tables 1–3 and refs. 1–19.
Rights and permissions
About this article
Cite this article
Löbl, M.C., Spinnler, C., Javadi, A. et al. Radiative Auger process in the single-photon limit. Nat. Nanotechnol. 15, 558–562 (2020). https://doi.org/10.1038/s41565-020-0697-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41565-020-0697-2
This article is cited by
-
Coherent control of a high-orbital hole in a semiconductor quantum dot
Nature Nanotechnology (2023)
-
Optically driving the radiative Auger transition
Nature Communications (2021)
-
Fundamental limits of electron and nuclear spin qubit lifetimes in an isolated self-assembled quantum dot
npj Quantum Information (2021)
-
Low-noise GaAs quantum dots for quantum photonics
Nature Communications (2020)
-
Auger processes in a single quantum dot
Nature Nanotechnology (2020)