Abstract
The presence of mobile ions in metal halide perovskites has been shown to adversely affect the intrinsic stability of perovskite solar cells (PSCs). However, the actual contribution of mobile ions to the total degradation loss compared with other factors such as trap-assisted recombination remains poorly understood. Here we reveal that mobile ion-induced internal field screening is the dominant factor in the degradation of PSCs under operational conditions. The increased field screening leads to a decrease in the steady-state efficiency, often owing to a large reduction in the current density. Instead, the efficiency at high scan speeds (>1,000 V s−1), where the ions are immobilized, is much less affected. We also show that the bulk and interface quality do not degrade upon ageing, yet the open-circuit voltage decreases owing to an increase in the mobile ion density. This work reveals the importance of ionic losses for intrinsic PSC degradation before chemical or extrinsic mechanical effects manifest.
Similar content being viewed by others

Main
Despite the impressive progress in terms of photovoltaic performance of perovskite solar cells over the last decade, there still remain many issues regarding the stability, which has considerable implications for their real-world energy yield1,2,3. These challenges include material decomposition under light4,5, heat6,7, oxygen8,9 and humidity10,11 or mechanical concerns such as delamination12 and strain13,14. Generally, increased trap-assisted recombination is also considered to be a major reason for degradation15,16,17,18. Efforts to improve device stability include compositional engineering19,20,21,22, device engineering23,24,25, the incorporation of two-dimensional perovskites26,27, diffusion barriers28,29,30,31 and more effective encapsulation methods32. However, the reported stability remains far below the targeted values required for commercial viability33 (International Electrotechnical Commission standards and ~25 year operational lifetime), highlighting the need for a more comprehensive understanding of the underlying chemical and physical processes occurring during device ageing and their effects on device performance.
Many of the intrinsic stability limitations are related to the presence of mobile ions in the perovskite layer, which behaves like a solid electrolyte with low activation energies for ionic transport34. For methylammonium lead iodide (MAPI), density functional theory simulations have predicted a mobile ion density (nION) of ~1 × 1019 cm−3 due to the low activation energy of the mobile ions (~100 meV)35, although most recent experimental/numerical studies narrow the mobile ions density to 1 × 1015 to 1 × 1017 cm−3 in devices with low levels of hysteresis36,37,38,39,40. Halide vacancies and interstitial iodine are usually considered to be the dominant species of mobile ions, and they are particularly harmful since they can form I2—a solid that easily sublimes above room temperature, leading to a loss of absorber layer material, potentially causing electrode cracks and critical device failure41. The migration and accumulation of halide defects due to lateral variation in the electric field also trigger degradation at the edges of cells and at the position of external impurities42. Moreover, A- and X-site mobile ions and vacancies are able to diffuse into the transport layers (TLs), with halide ions being localized in the device electrodes29,41,43,44,45,46. This effect may cause a range of problems, for example, loss of charge selectivity owing to a change in the electrode work function, oxidation reactions, corrosion or the formation of insulating layers. As such there is substantial research into ion migration in perovskites47,48,49,50.
Although tackling stability has always been a main priority for perovskite researchers, the community still lacks to some extent the experimental methodologies required to quantitatively characterize degradation losses induced by mobile ions to overcome these limitations. Moreover, it is not yet possible to decouple these losses from losses due to trap-assisted recombination and deterioration of other device and material parameters. In this regard, we recently presented a method to determine the contribution of mobile ion-induced efficiency losses to the device performance and showed that the presence of mobile ions leads to moderate efficiency losses in fresh devices with low levels of apparent hysteresis (typically 1–3% absolute)51. The underlying mechanism of these ion-induced losses is the movement of mobile ions to the perovskite–transport layer interfaces, leading to field screening and a reduction in charge extraction efficiency38,52,53,54,55,56,57.
In this Article, we determine the contribution of mobile ion-induced degradation losses to the total degradation loss in the presence of external stressors for a range of different perovskite solar cells. Using current density vs. voltage (J–V) measurements at different scan speeds, we first demonstrate that these losses can be directly linked to the movement of mobile ions and an increase in nION, which dominates the initial performance losses of perovskite solar cells. We show that an increased nION upon prolonged illumination leads to a substantial decrease in the steady-state power conversion efficiency (PCE), mainly owing to a large reduction in short-circuit current density (JSC) from fast to slow scan speeds that can exceed 10 mA cm−2. We attribute this result to increased field screening—a phenomenon that, to the best of our knowledge, has not been previously discussed in relation to the degradation of perovskite solar cells. We also show that interfacial recombination does not increase upon ageing, yet there is an increasing mismatch between open-circuit voltage (VOC) and the quasi-Fermi level splitting (QFLS), which can also be attributed to an increased accumulation of ions in the contact regions. As such, the increasing nION dominates the early ageing stages of perovskite solar cells. This work establishes key insights into the process of device degradation and the critical role mobile ions play therein and lays the foundation for accelerated ageing tests to predict the long-term stability of perovskite devices on the basis of a quantitative analysis of ion-induced losses.
Ionic losses during degradation
To study the effects of illumination-induced degradation in perovskite solar cells, we started off investigating the commonly used triple-cation Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3 1.63 eV perovskite composition in a pin-type architecture (referred to as ‘83:17 TC’ throughout). The following cell architecture was used: indium tin oxide (ITO)/PTAA/PFN-Br/perovskite/C60/BCP/Cu, that is, indium tin oxide/poly[bis(4-phenyl)(2,4,6-trimethylphenyl)amine]/poly((9,9-bis(3′-(N,N-dimethyl)-N-ethylammonium-propyl)-2,7-fluorene)-alt-2,7-(9,9-dioctylfluorene)) dibromide/perovskite/C60/bathocuproine/Cu58. The cells were subjected to three different external stressors: light, heat and electrical bias, with a focus on light-induced degradation. During the light-induced ageing, devices were exposed to 1 sun illumination at VOC and cooled such that the device temperature remained at 25 °C. Measurements under maximum power point conditions (MPP) are discussed further below. In Fig. 1a, the stabilized J–V curves (without hysteresis) at slow scan speeds (10 mV s−1) after different illumination times under VOC are exemplified. Figure 1b shows how the different device parameters change over time with ageing. In these cells, the increasing JSC losses over time dominate the degradation losses although fill factor (FF) losses are also significant, and the VOC decreases slightly as well.
a, Representative stabilized J–V characteristics at slow scan speeds (10 mV s−1) measured on a fresh Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3 perovskite solar cell as well as after continuous illumination at VOC for the specified time. b, Relative steady-state losses of the different PCE parameters as a function of ageing time.
To quantify the impact of mobile ions on the light-induced performance degradation, we performed fast hysteresis (FH) J–V measurements at different points in time during the ageing process. While details are presented in Methods and in ref. 51, we note that the cell is initially held slightly above the initial VOC (pre-bias), followed by a reverse and forward sweep with variable frequency or scan speed. The duration of the pre-bias was 5× longer than the total scan time of the voltage sweep. The methodology allows us to determine the steady-state and the ‘ion-freeze’ efficiency, which refers to the condition at which the ions are effectively immobilized when the scan rate is much quicker than the diffusion rate51. The difference between slow (steady-state) and fast scan speeds can be directly attributed to the movement of mobile ions and is referred to as mobile ion-induced PCE loss (Lion = ηion-freeze − ηsteady-state) in the following51.
However, it should be noted that the presence of mobile ions can still affect the PCE even when they are immobilized, depending on their distribution and accumulation throughout the device and at the interfaces51,56. This effect will be small if the ions are homogeneously distributed in the bulk at the start of the scan, which is discussed further below. The results (Fig. 2a) reveal once again that the steady-state efficiency drops significantly with ageing. Conversely, the ion-freeze efficiency, determined at fast scan speeds of around 2,500 V s−1, experiences a much smaller, almost negligible reduction. Next, we investigated the effects on each of the three J–V metrics: the VOC, JSC and FF, displayed in Fig. 2b–d. It can be seen that the performance losses are largely related to a drastic loss of the steady-state current output with respect to the ion-freeze JSC (even >10 mA cm−2 current loss can be observed in other systems as discussed below). However, the VOC and the FF are also affected to some extent. Furthermore, the ‘peak hysteresis’, that is, the maximum difference between the PCE determined from the forward versus the reverse scan, also increases significantly with ageing (Fig. 2a). Overall, the remarkable difference in the PCE between the fast and slow scan speeds (Fig. 2e,f) shows that the dominant loss mechanism upon ageing acts more significantly at the slower timescales.
a–d, The PCE (a), JSC (b), VOC (c) and FF (d) obtained from J–V characteristics measured at different scan speeds in reverse (squares) and forward (circles) scan direction for Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3 perovskite solar cells after different ageing times. e, The absolute PCE at fast and slow timescales versus aging time. The coloured areas underneath the curves demonstrate large losses induced by the movement of mobile ions at slow scan speeds (blue curve) and small losses at fast scan speeds (red curve). f, Exemplified scan rate-dependent J–V curves after 480 min of ageing. The steady-state and ion-freeze PCE are defined at slow and fast scan speeds at which the hysteresis disappears, respectively. This is exemplified by the dashed horizontal lines at 480 min of ageing for the PCE and JSC in a and b, respectively. The transition from slow and fast scan speeds is highlighted by the shaded background in a. The peak hysteresis shows the maximum difference between the forward and reverse scan PCE as exemplified by the vertical arrow at 480 min of ageing. The ionic loss in PCE and JSC is obtained from the difference in the steady-state and ion-freeze state as shown by the vertical arrows in a, b and the shading in b.
To get some understanding of the chemical changes of the perovskite film during light exposure, we performed absorption spectroscopy (Supplementary Fig. 1), X-ray diffraction measurements on fresh and aged perovskite layers (Supplementary Fig. 2), scanning electronic microscopy and atomic force microscopy measurements (Supplementary Fig. 3). While these measurements do not rule out changes in the morphology, these changes are considered to be relatively small on the timescale of the measurements (up to 24 h of illumination).
To generalize these findings, we then investigated the mobile ion-induced ageing loss in a range of different perovskite compositions beyond the ‘83:17’ model system. These perovskite systems include a standard 1.6 eV MAPbI3 (‘MAPI’), a 1.69 eV double cation perovskite FA0.85Cs15Pb(I77Br23)3 (‘CsFA’) relevant for silicon/perovskite tandems, a wide-bandgap Cs0.05(FA0.60MA0.40)0.95Pb(I0.60Br0.40)3 (‘1.8 eV’) relevant for all-perovskite tandems and a high-performance (>22% PCE) 1.57 eV formamidinium lead iodide-rich (‘95:5 TH‘) triple halide perovskite (Cs0.05(FA0.95MA0.05)0.95Pb(I0.95Br0.05)3 + 20 wt% methylammonium chloride (MACl)). The FH results on all systems are shown in Supplementary Figs. 4–7. MPP tracking of all devices can be found in Supplementary Fig. 8. We also investigated nip-type cells (Supplementary Fig. 9), where we observed the same losses. These results demonstrate that the increase of the ionic loss contributes significantly to the degradation loss for all systems (Fig. 3a). Moreover, we find that the reduced JSC is the most important factor contributing to the ion-induced loss in these systems (Supplementary Figs. 10 and 11). However, the ionic loss may also predominately affect other PCE parameters depending on the exact material/device parameters. Moreover, some of the systems are probably affected by non-ionic losses, which likely affect the FF at fast scan speeds as discussed in Supplementary Note 1. Figure 3b exemplifies the large reduction of the steady-state JSC after several hours of illumination (5 h, except for 12 h in MAPI) with respect to the initial current.
a, The relative ageing-induced ionic loss (1 − PCEslow/PCEfast) as a function of ageing time under 1 sun open-circuit conditions demonstrates increasing ionic losses in all systems, though with varying magnitude depending on the individual composition. The highest ageing-induced ionic losses are found in the Cs0.05(FA0.60MA0.40)0.95Pb(I0.60Br0.40)3 (‘1.8 eV’) cell, followed by FA0.85Cs0.15Pb(I0.77Br0.23)3 (‘CsFA’), and 83:17 TC with the smallest losses found in MAPbI3 (‘MAPI’) and the Cs0.05(FA0.95MA0.05)0.95Pb(I0.95Br0.05)3 + 20 wt% MACl (‘95:5 TH’) cell, where the ion-induced ageing losses do not increase on these timescales. b, The JSC measured at different scan speeds for fresh and aged cells after 5 h of ageing under 1 sun open-circuit conditions (12 h for MAPI) with additional PCE parameters shown in Supplementary Fig. 4–7.
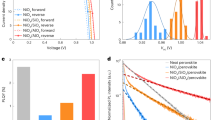
Importantly, Fig. 4a shows that the ionic losses also emerge in the much more stable 95:5 TH perovskite system, which degraded to roughly 68% of its initial PCE (21%) after tracking the stabilized power output (SPO) over 1,630 h. Notably, the PCE increased to 23.5% after roughly 50 h. The FH measurements taken initially and after the MPP tracking (Fig. 4b) reveal a nearly unchanged ion-freeze PCE, meaning that the observed degradation loss (here defined as \({L}_{{\rm{total}}}={\eta }_{{\rm{ion}}{\mbox{-}}{\rm{freeze}}}^{0}-{\eta }_{{\rm{steady}}{\mbox{-}}{\rm{state}}}^{f}\), where \({\eta }_{{\rm{ion}}{\mbox{-}}{\rm{freeze}}}^{0}\) and \({\eta }_{{\rm{steady}}{\mbox{-}}{\rm{state}}}^{f}\) are the initial ion-freeze and the final steady-state PCE, respectively) can be attributed to ionic losses (that is, Lion/Ltotal = 100%). Using a specific interlayer between the perovskite and C60 (described in a separate work), we then improved the initial VOC to 1.2 V and the performance of this device to a certified PCE of 24% and measured the ionic losses at the beginning and the end of the tracking (Supplementary Fig. 12). The device experienced a critical device failure due to electrode oxidation (thinning of the electrode owing to insufficient encapsulation visible by the eye) before we conducted the FH measurement at roughly 1,000 h. Nevertheless, the ionic losses still increase substantially during aging: Lion/Ltotal = 37.4%.
a, SPO tracking on the 95:5 TH device with enhanced stability compared with the 83:17 TC reference cell. Inset: The corresponding PCE and JSC from FH measurements at different scan speeds before and after the aging. b, SPO tracking on the 98:2 TH device and corresponding PCE and JSC at different scan speeds before and after the aging in the inset. The measurements demonstrate that the observed degradation stems largely from ionic losses while the ion-freeze PCE remains nearly unchanged. The dashed line is a guide to the eye, connecting the experimentally measured initial and final ion-freeze PCE (stars), while the gradient shading highlights the expected emergence of the ionic losses. The steady-state and ion-freeze PCE are marked by the diamonds and stars, respectively. The red arrows highlight the ionic losses after the degradation. The latter are determined from the difference between the steady-state and ion-freeze PCE, as exemplified by the yellow horizontal lines in the insets. The experimental conditions for the SPO and FH measurements can be found in Methods and all the remaining FH data in Supplementary Fig. 14.
In an attempt to generalize the findings further, we performed additional measurements on a high-performance pin-type Cs0.05(FA0.98MA0.02)0.95Pb(I0.98Br0.02)3 cell (‘98:2 TH’) fabricated in our laboratory, as well as Cs0.05(FA0.95MA0.05)0.95Pb(I0.95Br0.05)3 cells made at the East China University of Science and Technology (‘95:5 ECUST’)59. The results, highlighted in Fig. 4c,d and in Supplementary Fig. 13 for the 98:2 TH and the 95:5 ECUST device, respectively, demonstrate dominant ionic losses in both cells, that is, \({L}_{{\rm{ion}}}/{L}_{{\rm{total}}}\) = 73.1% and 81.3% after tracking the SPO of the 98:2 TH cell for 270 h and the MPP of the 95:5 ECUST cell for 1,000 h, respectively. The remaining FH data corresponding to Fig. 4 can be found in Supplementary Fig. 14. Overall, these results confirm that the same losses also occur in more stable cells during MPP or SPO tracking, and in cells fabricated in other laboratories. The results indicate that the ionic losses are even more critical in stable cells, which do not undergo premature degradation due to extrinsic issues such as shunt formation, moisture ingress or electrode corrosion, which can cause earlier device failure.
Understanding reasons for ionic losses
Having established that the ionic losses play a key role for the intrinsic device degradation, we now set out to understand the origin of these losses. At this point, it is important to note that the increase of the ionic loss with ageing time could be due to different factors51. This is because the magnitude of the ionic loss depends on various device and material parameters for a given ion density. To identify the underlying mechanisms, we now discuss, simulate and analyse distinct scenarios. For the simulations, we used the software IonMonger60 and cross-checked using the software SETFOS from FLUXiM61. In our first hypothesis, the concentration of mobile ions increases with ageing, which leads to enhanced ionic losses as shown by the simulations in Fig. 5a (see Supplementary Fig. 15, Supplementary Fig. 16 and Supplementary Table 1 for the J–V characteristics, the corresponding PCE parameters and the simulation parameters, respectively). Here, the increased nION causes enhanced screening of the internal electric field in the absorber layer, leading to a continuous reduction in the charge extraction efficiency due to band flattening (Supplementary Fig. 17).
a, The simulated PCE at different scan speeds in reverse (solid lines) and forward scan (dashed lines) direction for a range of different mobile ion densities. We consider mobile halide vacancies in our simulations with counter-ions being immobilized; however, the observed trend does not depend on the sign of the dominant mobile ion species or if there are one or two mobile species. b, Simulated PCE from J–V curves at different scan speeds in reverse (solid line) and forward scan (dashed line) direction for a range of different recombination velocities (S) at both perovskite–transport layer interfaces. The arrow highlights the ionic loss. c, Device VOC and the QFLS measured with PL on bare triple-cation films (‘pero’), and partial (‘HTL/pero’ and ‘Pero/C60’) and complete cell stacks (structures shown in the inset) as a function of illumination time. The arrow marks the QFLS–eVOC difference in the cell.
Another possible explanation for the enhanced ionic losses is degrading perovskite/transport layer interfaces with higher recombination velocities (S). As shown in Fig. 5b, the increased recombination velocity leads to a reduced steady-state PCE and increased peak hysteresis. However, in contrast to the case of an increased nION (Fig. 4a), the ion-freeze PCE at fast scan speeds decreases as well. In addition, we also investigated the impact of an increased energy level offset, as well as the impact of more bulk defects lowering the bulk lifetime (Supplementary Fig. 18). We found that both effects (increased energy offset and reduced bulk lifetime) lead to a parallel downshift of the scan rate-dependent PCE rather than an increase in the ionic losses, which is not consistent with the experimental results.
To further investigate the impact of potentially worsening interfaces or absorber layer quality on the enhanced ionic losses, photoluminescence (PL) measurements of different partial cell stacks were recorded as a function of illumination time. From the PL yield, the quasi-Fermi level splitting (QFLS) was calculated following our previous methodology58,62. Surprisingly, the results (Fig. 5c) suggest that the interfaces do not significantly worsen as the QFLS of all the partial device stacks increases slightly over time, while the QFLS of the neat perovskite layer was nearly unchanged. This suggests that increased bulk and interfacial defects are probably not a dominant factor of the light-induced degradation in this cell. Yet, the device VOC decreases, resulting in an increasing QFLS–eVOC mismatch upon ageing62, which is intriguing. Although this requires further investigation, the QFLS–VOC mismatch provides clues about the effect of ions at fast scan speeds. The FH simulations displayed in Supplementary Fig. 19 shows that, if the built-in voltage (VBI) is not offset with the pre-bias of the FH measurement (that is, Vpre < VBI), the VOC decreases with increasing nION. Considering that such a VOC decrease (and QFLS–eVOC mismatch) is observed in various systems (Supplementary Figs. 4–7) points to ion accumulation in an unfavourable position under open-circuit conditions (for example, cations at the hole-selective interface)56,62.
Having ruled out an increased recombination velocity at the interfaces, an increased mobile ion density seems likely to be the root cause of the observed ageing-induced losses. To directly assess whether nION increases with degradation, we performed bias-assisted charge extraction (BACE)63,64 and charge extraction by linearly increasing voltage (CELIV) measurements at the same points in time as the FH measurements. Both techniques can be used to estimate the nION by integrating the external current. In BACE, the cell is held under ‘quasi’-open-circuit conditions, where the injection current equals the JSC at which the mobile ions are distributed throughout the absorber layer before the voltage is switched to 0 V, at which point the mobile ions drift to the contact layers. However, we note that, if the ionic charge is larger than the electrode charge (QION > CVBI), the formation of zero-field regions should limit the displacement of ions in excess of CVBI (ref. 65). Thus, CVBI is expected to be a natural limit for the externally detectable ionic charge. Moreover, the ratio of the drift length of charges versus the film thickness (ddrift/d) limits the externally integrated charge65. Therefore, the ions should be roughly homogeneously distributed under the pre-bias condition to maximize the drift length and to avoid an underestimation of nION (ref. 66).
The results of the BACE measurements are displayed in Fig. 6a. It can be seen that the externally measured current is greatly enhanced the longer the illumination. Notably, the ionic ‘time of flight’ in the fresh device at around 50 ms (Supplementary Fig. 20) matches nearly perfectly the scan time at the peak hysteresis observed in averaged FH on fresh devices (~50 ms). Owing to the associated diffusion constant (\(D\) = 7 × 10−10 cm s−1) and ionic mobility (\(\mu\) = 2 × 10−8 cm2 V s−1), these results indicate that the responsible ion species are consistent with halide vacancies40,48. Therefore, these measurements link the transient charge extraction with the scan rate-dependent J–V results. It is also interesting to note that, with prolonged ageing time, slower species are extracted. This is also consistent with a slowdown of the peak hysteresis that is observed in the FH measurements in Fig. 2a for the 83:17 TC and in Supplementary Fig. 6 for the 60:40 TC system. Considering that this is not observed in CsFA (Supplementary Fig. 5) might point to A-site vacancies40,48. Another possible explanation is that grain boundary diffusion is replaced by volume diffusion in less stable devices, which has recently been identified to have a two orders of magnitude lower ion diffusivity67. More details regarding the timescales observed in FH and BACE are discussed in Supplementary Note 2.
a,b, Current transients from BACE measurements for both fresh and aged devices (a) and integrated charge carrier density from the transients in a (b). The applied voltage pulse to the device is illustrated in the inset in a. Considering that the capacitive (dis)charging effect after the voltage switch and the extraction of electronic charges takes place on the microsecond timescales, the contribution to the total extracted charge in these transients is expected to be nearly entirely given by mobile ions51. The inset in b shows the ion density as a function of time. c, The ionic loss obtained for a Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3 triple-cation device as a function of the ion density reveals a linear dependence after an initial dwell ageing time.
As shown in Fig. 6b, by integrating the external current, a rough estimate for nION can be obtained. We note that we do not exclude some collection of ions from the side of the pixel as recently demonstrated, which could increase nION within the active device area42. It can be seen that nION increases significantly, even within the first hour of illumination, and reaches values over 1018 cm−3 after 20 h of ageing under light. Although the reason why such large densities can be obtained in BACE is not yet clear, considering the above-discussed limit of the detectable ion density, the obtained values make sense qualitatively. As shown in Fig. 4a, the simulations can well reproduce the observed losses at the given ion densities. To highlight the effect, an ion density of 5 × 1018 cm−3 approximately halves the initial steady-state PCE owing to enhanced ionic losses. By plotting the ionic losses obtained through FH as a function of nION in Fig. 6c, we observe a linear dependence after an initial dwell time. Moreover, an increase of nION with increasing ageing time was also confirmed for the other studied systems (Supplementary Fig. 21). Also from CELIV, the increasing ion density during ageing is reflected in the large increase in the signal on slower timescales, starting at roughly 1 × 10−4 s in the 83:17 TC cell (Supplementary Fig. 22)51.
To investigate whether the devices would age similarly under real-world conditions and to better understand the dominant factor triggering the degradation, we expanded our measurements to other ageing conditions: elevated temperatures (75 °C) in the dark (Supplementary Fig. 23), MPP conditions at 1 sun illumination (Supplementary Fig. 24) and electrical bias (VOC) in the dark (Supplementary Fig. 25). From these results, it becomes clear that the ion-induced performance loss is a general degradation mechanism that occurs under different stressors. Nevertheless, the ageing at elevated temperatures does not show the characteristic step-function like scan rate-dependent JSC (Supplementary Fig. 18) nor display a very large increase of nION on these timescales (Supplementary Fig. 26). This might point towards a different path of degradation or a slower evolution of the ionic losses.
While determining the exact rates of degradation requires a much more focused investigation, our measurements indicate that mobile ions are easily created in the presence of electrical charges in the active layer regardless of the presence of light. This is consistent with the interpretation that halide vacancies are generated by injected or photo-generated free holes45,47. It has been previously shown that iodine atoms can be oxidized and iodine kicked out of the lattice by photo-generated holes, creating halide vacancies via \(\mathrm{I}_{{\mathrm{I}}}^{x}+\mathrm{h}^{+}=\mathrm{I}_{i}^{x}+\mathrm{V}_{{\rm{I}}}^{+}\), where I, I and \(x\) refer to the regular and the interstitial lattice site and to the neutral charge, respectively34,45,47. Another possible ion source is unreacted lead halide PbI2 (Supplementary Fig. 2), which can decompose into metallic lead and mobile iodine under illumination18. Both of these mechanisms are consistent with additional X-ray photoelectron spectroscopy measurements, which reveal the presence of iodine on top of the C60 layer after illuminating the triple-cation perovskite for approximately 10 h, demonstrating the possibility of iodine diffusion through fullerenes, in line with previous reports (Supplementary Fig. 27)29,68,69,70. Moreover, we could detect iodine in the perovskite film on a Si substrate that was placed ~1 mm above the sample (in N2) during illumination, hence highlighting the egress of volatile iodine species (Supplementary Fig. 28).
To recap, the mobile ion-induced efficiency losses dominate the early degradation losses in the here tested perovskite compositions, and on the basis of various measurements, such as PL and BACE, we attribute these enhanced ionic losses to an increasing ion density upon ageing. Figure 7a shows a breakdown of the identified degradation losses under illumination for the 83:17 TC system: (1) the ionic loss in JSC and FF, which is attributed to the field screening effect due to the movement of mobile ions, (2) the loss due to the QFLS–VOC mismatch, which is probably also a mobile ion-induced loss and (3) other, as yet unspecified, loss processes.
a, A breakdown of the loss processes: mobile ion-induced JSC and FF losses, mismatch of the QFLS and VOC that we also attribute to accumulation of ions at the interfaces, and other losses. b, A schematic band diagram of the HTL (red)/perovskite (purple)/ETL (blue) stacks at short-circuit conditions, highlighting the accumulation of cation vacancies at the HTL (p-)interface (red squares) that leads to enhanced hole (‘+’ circles) accumulation and electron (‘−’ circles) accumulation close to the HTL. The interfacial (Rinterface) and bulk recombination rate (Rbulk) are indicated by the purple arrows. The inset in b reveals the ion-free case where the dashed black line shows the QFLS. Here, EC and EV refer to the conduction and valence band, respectively. c, The simulated hole (dashed red lines) and electron (solid blue lines) density across the cell stack for different ion densities from 1 × 1015 cm−3 to 1 × 1018 cm−3 in logarithmic steps from light to darker colours in the direction of the arrow. d, The recombination current at the p-interface and in the bulk as a function of applied voltage for different ion densities. The graph highlights that interfacial (dot dashed lines) and bulk recombination (solid lines) increase with increasing ion density. However, the former is more significant, which is also indicated by the purple arrows in b.
Figure 7b–d schematically illustrates a possible explanation for the observed JSC and FF losses. The increased nION during the ageing successively screens the internal (built-in) field, thus increasing the fraction of the active layer that is effectively under VOC (or flat band) conditions. The formation of zero-field regions under short-circuit conditions leads to an increased accumulation of electronic charges (e− and h+) at the hole-selective interface. This charge accumulation leads in turn to enhanced recombination at the hole transport layer (HTL) and in the bulk. We note that the reason why the p-interface is more affected than the electron-selective interface is that we consider positively charged mobile ions (halide vacancies), which screen the field at the HTL. The dominance of mobile vacancies was confirmed by experiments performed by Senocrate et al.71, who measured the ionic conductivity in MAPI for various iodine partial pressures and found that incorporating more iodine decreases the ion conductivity by passivating mobile iodine vacancies. Similarly, Kamat et al. found that excess iodine suppresses mobile ion-related features in transient absorption spectroscopy72. Therefore, we suspect that halide vacancies are the problem. However, currently, we do not exclude negative ions as dominant ionic species, in which case, the electron-selective interface would be more significantly affected. Finally, while there might be some small bulk recombination losses at short-circuit conditions depending on the diffusion length in the absorber layer, the recombination at the interfaces increases more rapidly with the increasing cation vacancy concentration at 0 V (Fig. 6d). Moreover, the interfacial recombination current scales faster with the applied forward bias than the bulk losses, thus affecting the FF more significantly (Fig. 6d).
To explain the observed QFLS–VOC mismatch with increased ion densities, we analysed the band diagrams at VOC conditions displayed in Supplementary Fig. 29 for devices with different ion densities. The graph shows that a higher cation vacancy concentration causes a larger electron QFL bending at the C60 interface (\(\nabla {E}_{{\rm{f}},{\rm{e}}}\)). This can be explained by a population inversion at the electron-selective interface, that is, enhanced hole accumulation and depletion of electrons (Supplementary Fig. 30), and \(\nabla {E}_{{\rm{f}},{\rm{e}}}=\frac{{\sigma }_{\rm{h}}}{{\sigma }_{\rm{e}}}\cdot \nabla {E}_{{\rm{f}},{\rm{h}}}\)73,74,75, where σh/e and ∇Ef,h are the hole/electron conductivity and the hole QFL bending, respectively). This suggests that mobile ions are probably also responsible for the observed QFLS–VOC mismatch and the reduction of the VOC. Therefore, parts of the losses at fast scan speeds are attributed to this ion accumulation.
Implications for improving device stability
Having thoroughly studied the impact of mobile ions on device degradation, it is also important to consider how this knowledge can translate into more stable devices. We first tested the above hypothesis that the ionic losses are strongly affected by the quality of the HTL/perovskite interface. To this end, we improved the p-interface by replacing the HTL PTAA with the self-assembled monolayer 2PACz (Supplementary Fig. 31). This readily improved the PLQY of the half stack and significantly slowed the ion-induced degradation losses. This is consistent with the assumption that the p-interface plays a major role in mediating the ion-induced losses.
Secondly, owing to the large impact of ion migration on the stability, we believe that the ionic properties are strongly correlated to the stability of the devices and that initial assessment of the ionic properties will allow us to rapidly identify more stable compositions. To exemplify this, our data in this work highlight a clear correlation between the magnitude of the peak hysteresis—where the ion migration is most harmful to the cell performance—and the T80 lifetime at which the PCE drops to 80% (Supplementary Fig. 32). Although a correlation between stability and hysteresis has been often observed in literature67,76, we emphasize that the full peak of the hysteresis cannot be resolved with commonly used source measure units for cell characterization (with maximum scan speeds usually below ~1 V s−1). Also depending on the effective ion diffusion coefficient in the used absorber, the peak hysteresis can shift by orders of magnitude in scan speed range. Thus, assessing the hysteresis at only one scan rate or a small scan speed range does not provide the true magnitude of the hysteresis and does not allow comparison of different perovskite devices with very different ion diffusion coefficients77. This is exemplified in Supplementary Fig. 32b, where it appears that the much more stable 95:5 TH device has a larger hysteresis compared with the 60:40 device at slow scan speeds typically used (100 mV s−1). This underlines the importance of closing the hysteresis at slow and fast scan speeds to understand the impact of the hysteresis on the device’s performance and stability. Lastly, we believe that reporting these ionic properties will allow the community to train a more accurate machine learning algorithm that can accelerate the development of a more stable composition78,79,80,81. Overall, while the correlation of ionic properties and long-term stability requires a much larger data set, which is beyond the scope of this present work, we believe that future research will allow us to identify highly stable perovskites on the basis of the ionic features and properties of newly developed devices.
Conclusion
In this work, we investigated the impact of mobile ions on the ageing-induced performance degradation of perovskite solar cells under different external stressors, with a focus on light-induced degradation, and thoroughly studied the mechanisms underlying the observed losses. We reveal a key degradation mechanism as a dominant factor for the intrinsic, early degradation that has previously not been clearly identified, namely mobile ion-induced field screening. This degradation loss appears to be more significant than increased trap-assisted recombination in the bulk and at the interfaces.
The ionic losses typically manifest as a strongly reduced JSC, which often suffers most significantly under the illumination in the studied compositions, although the FF and VOC are also affected by the mobile ions. With regard to the voltage losses, we found that they are caused by an increased QFLS–VOC mismatch due to ion accumulation, and not due to increased interfacial or bulk defects. This QFLS–VOC mismatch occurs in various systems and can be explained by an increased ion accumulation at the interfaces. Using different transient charge extraction techniques, we then linked the increasing current and FF losses upon ageing to an increase in the concentration of mobile ions in the perovskite. We showed that the increase of nION upon ageing is a general degradation mechanism, which occurs through exposure to other stressors, such as electrical bias. However, the ion-induced losses are more significant in the presence of free electrical charges and less under elevated temperatures, consistent with previous findings of halide vacancy generation through holes.
In the future, perovskite solar cells need to be engineered to minimize both the mobile ion densities that can be generated during ageing as well as their impact on the device performance. Our results also highlight the key role of the hole-selective interface for the non-induced degradation in case of large halide vacancy concentrations. By providing a crucial understanding of the role of mobile ions during degradation, this work paves the path to rapidly identify stable perovskite compositions based on the initial ionic fingerprints and highlights potential mitigation routes to prevent degradation, which will be key for the commercialization of perovskite-based solar cells.
Methods
Device fabrication of pin-type cells
Pre-patterned 2.5 × 2.5 cm2 15 Ω sq−1 ITO substrates (Automatic Research) were cleaned with acetone, 3% Hellmanex solution, deionized water and isopropanol by sonication for 10 min in each solution. After a microwave plasma treatment (3 min, 200 W), the samples were transferred to a N2-filled glovebox. For tall pin-type cells, except for the 95:5 TH and the 98:2 TH perovskite, a PTAA (Sigma-Aldrich) layer with a thickness of 8 nm was spin-coated from a 1.5 mg ml−1 PTAA/toluene solution at 6,000 rpm for 30 s. After 10 min annealing on a hotplate at 100 °C, the films were cooled down to room temperature, and a 60 µl solution of PFN-Br (1-Material, 0.5 mg ml−1 in methanol) was deposited onto PTAA while the substrate was being spun at 5,000 rpm for 20 s, resulting in a film with thickness below the detection limit of our atomic force microscopy (<5 nm). No further annealing occurred. For the 95:5 TH and the 98:2 TH perovskite, the same ITO-coated samples were used, but instead of the microwave plasma treatment, the substrates were treated with ultraviolet ozone for 30 min. The samples were then transferred to a nitrogen-filled glovebox and 100 μl MeO-2PACz purchased from TCI (0.003 g per 3 ml in ethanol) was spin-coated onto the ITO substrates at 3,000 rpm for 30 s, followed by annealing at 100 °C for 10 min. All fabrication details of the 95:5 ECUST cells based on (2-(4-(bis(4-methoxyphenyl)amino)phenyl)-1-cyanovinyl)phosphonic acid (MPA-CPA) are described in ref. 59.
The triple-cation perovskite solutions were prepared by mixing two 1.2 M FAPbI3 and MAPbBr3 perovskite solutions in dimethylformamide (DMF):dimethyl sulfoxide (DMSO) (4:1 volume ratio, v/v) in a ratio of 83:17 (for the 83:17 triple-cation reference cell) and 60:40 (for the 1.8 eV WG cell). The 1.2 M FAPbI3 solution was thereby prepared by dissolving FAI (722 mg) and PbI2 (2130 mg) in 2.8 ml DMF and 0.7 ml DMSO, which contains a 10 molar% excess of PbI2. The 1.2 M MAPbBr3 solution was made by dissolving MABr (470 mg) and PbBr2 (1,696 mg) in 2.8 ml DMF and 0.7 ml DMSO, which contains a 10 mol% excess of PbBr2. Lastly, 40 µL of a 1.5 CsI solution in DMSO (389 mg CsI in 1 ml DMSO) was mixed with 960 µL of the MAFA solution, resulting in a nominal perovskite stoichiometry of Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3 in case of the 83:17 triple-cation reference cell and Cs0.05(FA0.6MA0.4)0.95Pb(I0.6Br0.4)3 in case of the 1.8 eV WG cell. The MAPI solution was prepared by dissolution of MAI powder (Dysol, 0.2) with PbI2 (TCI America, 1.1 M) in a γ-butyrolactone/dimethyl sulfoxide mixed solvent (7:3 by volume) at 60 °C for 10 min. The Cs0.15FA0.85Pb(I0.75Br0.25)3 double cation perovskite was prepared by mixing PbI2 (TCI), FAI (Greatcell Solar), FABr (Sigma-Aldrich) and CsI (Sigma-Aldrich), with molarity ratios of 1.1, 0.12, 0.73 and 0.15, respectively, in one vial and adding a mixture of DMF:DMSO 4:1 in volume. The ‘95:5 triple halide (TH)’ perovskite precursor solution was prepared by mixing two 1.5 M FAPbI3 and MAPbBr3 perovskite solutions in DMF:DMSO (4:1 volume ratio, v/v) as well as the solution of CsI (1.5 M), resulting in a nominal perovskite stoichiometry of Cs0.05(FA0.95MA0.05)0.95Pb(I0.95Br0.05)3. Then, 20 molar% MACl (Merck) dissolved in DMSO was added into the precursor solution to improve the crystallization of the film. All final solutions were stirred overnight at room temperature. For the ‘98:2 triple halide (TH)’ perovskite precursor solution, 1.73 M \({{\rm{Cs}}}_{0.05}({{\rm{FA}}}_{0.98}{{\rm{MA}}}_{0.02})_{0.95}\)Pb\(({{\rm{I}}}_{0.98}{{\rm{Br}}}_{0.02})_{3}\) perovskite precursor was prepared by dissolving 0.90919 g lead iodide (PbI2, TCI), 0.27698 g formamidinium iodide (FAI, GreatCell Solar), 0.02247 g caesium iodide (CsI, Sigma-Aldrich), 0.00368 g methylammonium bromide (MABr, GreatCell Solar) and 0.018105 g MACl (Merck) in a 4:1 (by volume) mixture solvent of DMF (anhydrous, 99.8%; Sigma-Aldrich) and DMSO (anhydrous, ≥99.9%; Sigma-Aldrich). The precursor solution was stirred 780 rpm on the hotplate for 4 h at 55 °C and then filtered. All solution preparation processes were conducted in a N2 glovebox (O2 <1 ppm and H2O <1 ppm)
Both triple-cation films (83:17 TC and 1.8 eV WG) were deposited by spin-coating at 5,000 rpm for 35 s, and 10 s after the start of the spinning process, the spinning substrate was washed with 300 µl ethyl acetate for approximately 1 s (the anti-solvent was placed in the centre of the film). We note that, by the end of the spinning process, the perovskite film turned dark brown. The perovskite film was then annealed at 100 °C for 1 h on a pre-heated hotplate, where the film turned slightly darker. The MAPI solution (80 μl) was spin-coated at 1,000 rpm for 5 s followed by 3,000 rpm for 80 s. A total of 100 μl toluene was added dropwise after 40 s to form a transparent perovskite film. After the spin coating, the films were dried for 2 min in the glovebox at room temperature until the films changed their colour from yellow to light brown. The MAPI perovskite layers were then subsequently annealed at 100 °C on a hotplate, where the films turned black immediately. For the Cs0.15FA0.85Pb(I0.75Br0.25)3 perovskite, a volume of 120 μl of the precursor solution was spin-coated at 4,000 rpm (with a ramping rate of 1,334 rpm s−1) for 40 s. After 10 s, the film was quenched by adding 300 μl of ethyl acetate. Directly afterwards, the film was annealed at 100 °C for 60 min inside the N2 filled glovebox. For the 95:5 TH perovskite, 120 μl of the perovskite precursor was spin-coated onto the cooled (HTL-coated) substrates at 4,000 rpm for 40 s (5 s acceleration to 4,000 rpm). A total of 200 μl anti-solvent chlorobenzene was slowly dripped onto the centre of the film 7 s before the end of the spinning programme. Further, the perovskite film was annealed at 100 °C for 60 min. The 98:2 TH \({{\rm{Cs}}}_{0.05}({{\rm{FA}}}_{0.98}{{\rm{MA}}}_{0.02})_{0.95}\)Pb \(({{\rm{I}}}_{0.98}{{\rm{Br}}}_{0.02})_{3}\) films were fabricated by spin-coating a volume of 100 μl of the precursor solution onto the cooled (HTL-coated) substrates via two steps: 100 rpm 334 rpm s−1 for 10 s and 5,000 rpm 2,000 rpm s−1 for 40 s at the second leg of the spinning process. The perovskite film turned dark brown, and it was subsequently annealed at 100 °C for 20 min on a pre-heated hotplate, where the film turned black immediately.
Only the 98:2 TH perovskite included a passivation consisting of 0.002 g ethane-1,2-diammonium iodide (EDAI2) purchased from Sigma-Aldrich dissolved in 1 ml of isopropanol (99.5%) and 1 ml toluene (anhydrous, 99.8%,) and then stirred in the ultrasonic bath for 25 min. The 120 µl solution of EDAI2 (0.002 g ml−1 in isopropanol/toluene) was then deposited onto perovskite while the substrate was being spun at 5,000 rpm, 4,000 rpm s−1 for 30 s. After 5 min annealing on a hotplate at 100 °C, the films were cooled down to room temperature.
After annealing, all samples were transferred to an evaporation chamber where fullerene-C60 (30 nm), 2,9-dimethyl-4,7-diphenyl-1,10-phenanthroline BCP (8 nm) and copper (100 nm) were deposited under vacuum (pressure of 1 × 10−7 mbar). The overlap of the copper and the ITO electrodes defined the active area of the pixel (6 mm2).
Device fabrication of nip-type cells
TEC15 FTO glass was used. Glass substrates were cleaned and ultraviolet ozone treated for 15 min before electron transport layer (ETL) deposition. A total of 100 µl of titanium isopropoxide solution (diluted 1:15 in 1-butanol) was statistically spin-coated at 5,000 rpm for 45 s (acceleration of 2,000 rpm s−1) then dried at 130 °C for 5 min and 450 °C for 30 min 100 µl of SnO2 nanoparticle dispersion (2 wt% diluted in deionized water) were spin-coated at 4,000 rpm for 30 s (acceleration of 3,000 rpm s−1) and then annealed at 180 °C for 30 min. Then, 1.5 M (FAPbI3)0.99(CsPbBr3)0.01:35 mol% MACl (1.53 eV perovskite) were stoichiometrically weighed and dissolved in DMF:DMSO (4:1 by volume). It was stirred for 1 h and filtered (0.45 µm, PTFE) before use. A total of 100 µl of the solution was dropped dynamically. The spin was conducted in two steps: 1,000 rpm for 10 s (acceleration of 500 rpm s−1) and 5,000 rpm for 35 s (acceleration of 1,000 rpm s−1). Then, 300 μl of anisole was used for solvent quenching at 5 s before the end of the spin. It was annealed at 80 °C for 10 min. This was performed in the glovebox, followed by further annealing at 150 °C for 15 min in the dry box (RH <5%). A 2,2′,7,7′-tetrakis[N,N-di(4-methoxyphenyl)amino]-9,9′-spirobifluorene (Spiro-OMeTAD) solution was prepared with the following composition: 60 mg of Spiro-OMeTAD, 25.5 μl of 4-tert-butylpyridine, 15.5 μl of Li-TFSI (520 mg ml−1 in acetonitrile) and 12.5 μl of Co-TFSI (375 mg ml−1 in acetonitrile) in 700 μl of chlorobenzene. A total of 60 μl of the solution was dynamically spin-coated at 4,000 rpm for 30 s, then dried overnight in dry air condition before Au deposition. The devices were completed with 70-nm-thick thermally evaporated Au.
Current density–voltage characteristics
Curves were obtained in a two-wire source-sense configuration with a Keithley 2400 (standard J–V characterization). An Oriel class AAA xenon-lamp-based sun simulator was used for illumination, providing approximately 100 mW cm−2 of simulated AM1.5G irradiation as calibrated using a (KG3) filtered Si reference certified from Fraunhofer Institute for Solar Energy Systems (ISE). The intensity was further monitored simultaneously with a Si photodiode to use the exact illumination intensity for efficiency calculations. The device area of 6 mm2 was masked with a 4.32 mm2 mask, and the obtained short-circuit current densities were checked by integrating the product of the external quantum efficiency and the solar spectrum, which matches the obtained value within less than 5%. The temperature of the cell was fixed to 25 °C, and a voltage ramp (scan rate) of 67 mV s−1 was used. J–V curves obtained using different scan speeds and stabilization times are the subject of this work. For the 83:17 reference cell, a spectral mismatch calculation was performed on the basis of the spectral irradiance of the solar simulator, the external quantum efficiency of the reference silicon solar cell and three typical external quantum efficiencies of our cells. This resulted in three mismatch factors of M = 0.9949, 0.9996 and 0.9976. Given the very small deviation from unity, the measured JSC was not corrected by the factor 1/M.
FH measurements
Fast J–V curves were obtained by applying a triangular voltage pulse to the cells starting from approximately open-circuit (VOC) followed by a reverse sweep from open-circuit to −0.1 V and forward sweep from −0.1 V to VOC with variable frequency or scan speed (V s−1) using a system developed by FastChar UG. The duration of the hold voltage at VOC was five times longer than the total scan time of the voltage sweep. The voltage response of the cell was measured with an oscilloscope, using an external load resistance of ≤10 Ω, and the voltage pulse was supplied by a function generator in combination with a home-built power amplifier (4×). Despite the different hardware and measurement routines, the testing conditions were the same as used for the standard J–V measurements as described above. We note that, to cross-check the FH results at slow scan speeds (10–100 mV s−1), standard J–V measurements were performed on the same cells, which resulted in a nearly identical performance metric as obtained with the FH setup.
BACE
In dark BACE, the device was initially held at a voltage close to the open-circuit voltage, where the injected charge equals the short-circuit current. After a pre-set delay time, a bias of 0 V was applied to extract the injected and capacitive charge in the device. The delay times for the fresh devices were chosen to be typically five times longer than the extraction time of charges observed under the collection bias (typically ~5–10 s) to allow ionic charges to distribute throughout the active layer. The BACE measurements during the light aging (Fig. 6) were performed in the following way. First, while the cells were illuminated, a voltage close to the VOC was applied to the cells to prevent a premature extraction of mobile ions to the transport layers by the built-in voltage when the light source is switched off (as this would lower the extracted charge). Subsequently, the illumination was switched off; however, the built-in voltage remains roughly compensated by the applied voltage keeping the mobile ions roughly distributed throughout the bulk. Finally, after ~10 s, the voltage was switched to 0 V to extract the charge carriers. The current transients were measured with a Keithley 2400 using a home-built LabView program. The use of a current meter was found to be necessary over an oscilloscope to resolve the small ion drift currents, and we note that no significant differences were observed when the measurements were performed with a Keithley 485 picoamperemeter instead of the Keithley 2400. Finally, the extracted charge was obtained by integrating the current transient and the charge carrier density by dividing the total charge by the elementary charge and the cell volume.
Dark CELIV
In dark CELIV, the device was initially held at short-circuit conditions. Then, the voltage was increased linearly to minus 0.4 V (in reverse bias) using a pulse generator. The slope (A = ∆V/∆t) was thereby varied to assess a wide timescale range (Δt). The current transients were recorded with an oscilloscope (Agilent DSO9104H) and measured with a variable load resistance (RLoad = 50 Ω at short 10 µs pulses and up to 10 kΩ at 100 ms pulses) to keep the voltage response approximately constant. The increased load resistance reduces the time resolution at short times but allows for recording the response for long pulses. The continuous increase of the electrode charge leads to a step-like voltage response. The voltage response step of the cell is given by ∆V = ARLoadC, from which we calculated the capacitance of the cell (C). Equilibrium charges in the active layer (doping-induced electronic charge or mobile ions) lead to an additional bump in the voltage response.
Numerical drift–diffusion simulations
The simulations were performed using SETFOS61 and IonMonger, an open-source code developed by Nicola Courtier et al.60. Both programs numerically solve a system of three coupled equations, namely the Poisson equation, the continuity equation and the drift–diffusion equation82.
Absolute PL measurements
Excitation for the PL measurements was performed with a 520 nm continuous-wave laser (Insaneware) through an optical fibre into an integrating sphere. The intensity of the laser was adjusted to a 1 sun equivalent intensity by illuminating a 1-cm2-size perovskite solar cell under short-circuit and matching the current density to the JSC under the sun simulator for the 83:17 triple-cation device (22.0 mA cm−2 at 100 mW cm−2, or 1.375 × 1021 photons m−2 s−1). A second optical fibre was used from the output of the integrating sphere to an Andor SR393iB spectrometer equipped with a silicon charge-coupled device camera (DU420A-BR-DD, iDus). The system was calibrated by using a calibrated halogen lamp with specified spectral irradiance, which was shone into the integrating sphere. A spectral correction factor was established to match the spectral output of the detector to the calibrated spectral irradiance of the lamp. The spectral photon density was obtained from the corrected detector signal (spectral irradiance) by division through the photon energy (hf), and the photon numbers of the excitation and emission were obtained from numerical integration using MATLAB. In the last step, three fluorescent test samples with high specified PLQY (~70%) supplied from Hamamatsu Photonics were measured, where the specified value could be accurately reproduced within a small relative error of less than 5%.
Photoemission spectroscopy measurements
Photoemission experiments were performed at an ultrahigh vacuum system consisting of sample preparation and analysis chambers (both at a base pressure of 1 × 10−10 mbar) as well as a load lock (with a base pressure of 1 × 10−6 mbar). All of the samples were transferred to the ultrahigh vacuum chamber using a transfer rod under a rough vacuum (1 × 10−3 mbar). Ultraviolet photoemission spectroscopy was performed using a helium discharge lamp (21.22 eV) with a filter to reduce the photon flux and block visible light from the source hitting the sample. All spectra were recorded at room temperature and normal emission using a hemispherical Specs Phoibos 100 analyser, and the overall energy resolution was 140 meV.
Light ageing
Light ageing under open-circuit conditions was performed in a dedicated aging box in the glovebox under N2 atmosphere using white light-emitting diode (LED) array illumination providing a 1 sun equivalent intensity by matching the initial current of the cell to the JSC. The intensity of the LED was checked using a photodiode and remained stable over the course of the course of the measurement timescale (~24 h) in a sample holder. The cells were cooled to 25 °C over the course of the measurement using a Peltier element, but no significant changes in the degradation were observed without additional cooling or for encapsulated cells measured in the lab outside the glovebox.
Voltage and temperature ageing
Voltage ageing was performed by applying a voltage slightly above the open-circuit voltage to the cell, at which the injected charge equals the initial short-circuit current. Over the course of the ageing test (~24 h), the applied voltage was slightly adjusted to maintain an injection current of roughly JSC. The temperature aging was conducted by placing the cell on a hotplate at ~80 °C for the given amount of time.
SPO tracking
Long-term SPO tracking measurements were performed on 95:5 TH and 98:2 TH cells with a Botest multichannel analyser system (Botest Systems GmbH, EMU-8/ v2.3) with a constant applied voltage (initial VMP) using white light LED (3000K Cree CXB3590) illumination providing a 1 sun equivalent intensity by matching the initial current of the cell to the JSC under AM1.5G illumination. The temperature during the tracking was T = 40 °C, and the measurements were performed in an ambient atmosphere on encapsulated cells.
MPP tracking
In addition to the SPO tracking, MPP tracking was performed on 95:5 ECUST, interlayer-modified 95:5 TH, and reference cells. The devices were placed under a 1 sun equivalent white LED irradiation inside a nitrogen-filled glovebox for several days. Thereby, the cell is continuously held at 25 °C and its maximum power voltage was obtained from an initial J–V scan. Maximum power output was ensured by applying a small voltage perturbation (±5 mV) to the cell every 5 s. Depending on which voltage gave a higher power output, the applied voltage was either increased or decreased by 5 mV and then held at this voltage for the next 5 s. A home-built LabView program was used for these measurements. No significant changes were observed between aging under SPO or MPP conditions.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All data generated or analysed during this study are included in the published article and its Supplementary Information. Data sources for the main text figures are available via Figshare at https://figshare.com/s/cbfad738b0666ecf7f98 (ref. 83).
Code availability
The codes that support the findings of this study are available from the following links. Parameter files for IonMonger simulations are available at https://doi.org/10.25446/oxford.24359959.v2 and parameter files for SETFOS simulations at https://doi.org/10.25446/oxford.24361138.v1.
Change history
05 April 2024
In the version of the article initially published an incorrect version of the Supplementary Information was included. This has now been updated in the HTML version of the article.
References
Rong, Y. et al. Challenges for commercializing perovskite solar cells. Science 361, eaat8235 (2018).
Meng, L., You, J. & Yang, Y. Addressing the stability issue of perovskite solar cells for commercial applications. Nat. Commun. 9, 1–4 (2018).
Ling, J. K. et al. A perspective on the commercial viability of perovskite solar cells. Sol. RRL 5, 1–48 (2021).
Ruan, S. et al. Light induced degradation in mixed-halide perovskites. J. Mater. Chem. C. 7, 9326–9334 (2019).
Lang, F. et al. Influence of radiation on the properties and the stability of hybrid perovskites. Adv. Mater. 30, 1–22 (2018).
Misra, R. K. et al. Temperature- and component-dependent degradation of perovskite photovoltaic materials under concentrated sunlight. J. Phys. Chem. Lett. 6, 326–330 (2015).
Conings, B. et al. Intrinsic thermal instability of methylammonium lead trihalide perovskite. Adv. Energy Mater. 5, 1–8 (2015).
Ouyang, Y. et al. Photo-oxidative degradation of methylammonium lead iodide perovskite: mechanism and protection. J. Mater. Chem. A 7, 2275–2282 (2019).
Bryant, D. et al. Light and oxygen induced degradation limits the operational stability of methylammonium lead triiodide perovskite solar cells. Energy Environ. Sci. 9, 1655–1660 (2016).
Wang, Q. et al. Scaling behavior of moisture-induced grain degradation in polycrystalline hybrid perovskite thin films. Energy Environ. Sci. 10, 516–522 (2017).
Salado, M. et al. Impact of moisture on efficiency-determining electronic processes in perovskite solar cells. J. Mater. Chem. A 5, 10917–10927 (2017).
De Bastiani, M. et al. Mechanical reliability of fullerene/tin oxide interfaces in monolithic perovskite/silicon tandem cells. ACS Energy Lett. 7, 827–833 (2022).
Meng, W. et al. Revealing the strain-associated physical mechanisms impacting the performance and stability of perovskite solar cells. Joule 6, 458–475 (2022).
Steele, J. A. et al. Thermal unequilibrium of strained black CsPbI3 thin films. Science 365, 679–684 (2019).
Li, Z., Li, B., Wu, X., Sheppard, S. A. & Zhang, S. Organometallic-functionalized interfaces for highly efficient inverted perovskite solar cells. Science 420, 416–420 (2022).
Azmi, R. et al. Damp heat—stable perovskite solar cells with tailored-dimensionality 2D/3D heterojunctions—supplementary. Mater. Sci. 5784, 1–9 (2022).
Deng, Y. et al. Defect compensation in formamidinium–caesium perovskites for highly efficient solar mini-modules with improved photostability. Nat. Energy 6, 633–641 (2021).
Holovský, J. et al. Lead halide residue as a source of light-induced reversible defects in hybrid perovskite layers and solar cells. ACS Energy Lett. 4, 3011–3017 (2019).
Turren-Cruz, S.-H., Hagfeldt, A. & Saliba, M. Methylammonium-free, high-performance, and stable perovskite solar cells on a planar architecture. Science 362, 449–453 (2018).
Eperon, G. E. et al. Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 7, 982 (2014).
Yang, I. S. & Park, N. G. Dual additive for simultaneous improvement of photovoltaic performance and stability of perovskite solar cell. Adv. Funct. Mater. 31, 1–7 (2021).
Zhang, F. & Zhu, K. Additive engineering for efficient and stable perovskite solar cells. Adv. Energy Mater. 10, 1902579 (2020).
Byeon, J. et al. Charge transport layer-dependent electronic band bending in perovskite solar cells and its correlation to light-induced device degradation. ACS Energy Lett. 5, 2580–2589 (2020).
Huang, L. & Ge, Z. Simple, robust, and going more efficient: recent advance on electron transport layer-free perovskite solar cells. Adv. Energy Mater. 9, 1–31 (2019).
Li, Y., Xie, H., Lim, E. L., Hagfeldt, A. & Bi, D. Recent progress of critical interface engineering for highly efficient and stable perovskite solar cells. Adv. Energy Mater. 12, 1–31 (2022).
Chen, P. et al. In situ growth of 2d perovskite capping layer for stable and efficient perovskite solar cells. Adv. Funct. Mater. 28, 1–10 (2018).
Grancini, G. et al. One-year stable perovskite solar cells by 2D/3D interface engineering. Nat. Commun. 8, 1–8 (2017).
Gahlmann, T. et al. Impermeable charge transport layers enable aqueous processing on top of perovskite solar cells. Adv. Energy Mater. 10, 1903897 (2020).
Brinkmann, K. O. et al. Suppressed decomposition of organometal halide perovskites by impermeable electron-extraction layers in inverted solar cells. Nat. Commun. 8, 13938 (2017).
Arora, N. et al. Perovskite solar cells with CuSCN hole extraction layers yield stabilized efficiencies greater than 20%. Science 358, 768–771 (2017).
Wu, S. et al. A chemically inert bismuth interlayer enhances long-term stability of inverted perovskite solar cells. Nat. Commun. 10, 1161 (2019).
Cheacharoen, R. et al. Encapsulating perovskite solar cells to withstand damp heat and thermal cycling. Sustain. Energy Fuels 2, 2398–2406 (2018).
Duan, L. et al. Stability challenges for the commercialization of perovskite–silicon tandem solar cells. Nat. Rev. Mater. 8, 261–281 (2023).
Kim, G. Y. et al. Large tunable photoeffect on ion conduction in halide perovskites and implications for photodecomposition. Nat. Mater. 17, 445–449 (2018).
Walsh, A., Scanlon, D. O., Chen, S., Gong, X. G. & Wei, S. H. Self-regulation mechanism for charged point defects in hybrid halide perovskites. Angew. Chem. Int. Ed. 54, 1791–1794 (2015).
Weber, S. A. L. et al. How the formation of interfacial charge causes hysteresis in perovskite solar cells. Energy Environ. Sci. 11, 2404–2413 (2018).
Richardson, G. et al. Can slow-moving ions explain hysteresis in the current-voltage curves of perovskite solar cells? Energy Environ. Sci. 9, 1476–1485 (2016).
Calado, P. et al. Evidence for ion migration in hybrid perovskite solar cells with minimal hysteresis. Nat. Commun. 7, 1–10 (2016).
Tessler, N. & Vaynzof, Y. Insights from device modeling of perovskite solar cells. ACS Energy Lett. 5, 1260–1270 (2020).
Futscher, M. H. et al. Quantification of ion migration in CH3NH3PbI3 perovskite solar cells by transient capacitance measurements. Mater. Horiz. 6, 1497–1503 (2019).
Fu, F. et al. I2 vapor-induced degradation of formamidinium lead iodide based perovskite solar cells under heat-light soaking conditions. Energy Environ. Sci. 12, 3074–3088 (2019).
Jacobs, D. A. et al. Lateral ion migration accelerates degradation in halide perovskite devices. Energy Environ. Sci. 15, 5324–5339 (2022).
Mei, A. et al. Stabilizing perovskite solar cells to IEC61215:2016 standards with over 9,000-h operational tracking. Joule 4, 2646–2660 (2020).
Yang, T. Y., Gregori, G., Pellet, N., Grätzel, M. & Maier, J. The significance of ion conduction in a hybrid organic-inorganic lead-iodide-based perovskite photosensitizer. Angew. Chem. Int. Ed. 54, 7905–7910 (2015).
Dunfield, S. P. et al. From defects to degradation: a mechanistic understanding of degradation in perovskite solar cell devices and modules. Adv. Energy Mater. 10, 1–35 (2020).
Kato, Y. et al. Silver iodide formation in methyl ammonium lead iodide perovskite solar cells with silver top electrodes. Adv. Mater. Interfaces 2, 2–7 (2015).
Motti, S. G. et al. Controlling competing photochemical reactions stabilizes perovskite solar cells. Nat. Photonics 13, 532–539 (2019).
Reichert, S. et al. Probing the ionic defect landscape in halide perovskite solar cells. Nat. Commun. 11, 6098 (2020).
Tammireddy, S. et al. Temperature-dependent ionic conductivity and properties of iodine-related defects in metal halide perovskites. ACS Energy Lett. 7, 310–319 (2022).
Meggiolaro, D. et al. Iodine chemistry determines the defect tolerance of lead-halide perovskites. Energy Environ. Sci. 11, 702–713 (2018).
Le Corre, V. M. et al. Quantification of efficiency losses due to mobile ions in perovskite solar cells via fast hysteresis measurements. Sol. RRL 6, 2100772 (2022).
Thiesbrummel, J. et al. Universal current losses in perovskite solar cells due to mobile ions. Adv. Energy Mater. 11, 2101447 (2021).
Cave, J. M. et al. Deducing transport properties of mobile vacancies from perovskite solar cell characteristics. J. Appl. Phys. 128, 184501 (2020).
Moia, D. et al. Dynamics of internal electric field screening in hybrid perovskite solar cells probed using electroabsorption. Phys. Rev. Appl. 18, 044056 (2022).
Futscher, M. H., et al. Quantification of ion migration in CH3NH3PbI3 perovskite solar cells by transient capacitance measurements. Mater. Horiz. 6, 1497–1503 (2018).
Jacobs, D. A. et al. Hysteresis phenomena in perovskite solar cells: the many and varied effects of ionic accumulation. Phys. Chem. Chem. Phys. 19, 3094–3103 (2017).
Herterich, J., Unmüssig, M., Loukeris, G., Kohlstaedt, M. & Würfel, U. Ion movement explains huge Voc increase despite almost unchanged internal quasi-Fermi level splitting in planar perovskite solar cells. Energy Technol. 9, 2001104 (2021).
Stolterfoht, M. et al. Visualization and suppression of interfacial recombination for high-efficiency large-area pin perovskite solar cells. Nat. Energy 3, 847–854 (2018).
Zhang, S. et al. Minimizing buried interfacial defects for efficient inverted perovskite solar cells. Science 380, 404–409 (2023).
Courtier, N. E., Cave, J. M., Walker, A. B., Richardson, G. & Foster, J. M. IonMonger: a free and fast planar perovskite solar cell simulator with coupled ion vacancy and charge carrier dynamics. J. Comput. Electron. 18, 1435–1449 (2019).
Aeberhard, U. et al. Numerical optimization of organic and hybrid multijunction solar cells. in 2019 IEEE 46th Photovoltaic Specialists Conference 0105–0111 (IEEE, 2019).
Stolterfoht, M. et al. The impact of energy alignment and interfacial recombination on the internal and external open-circuit voltage of perovskite solar cells. Energy Environ. Sci. 12, 2778–2788 (2019).
Li, B. et al. Revealing the correlation of light soaking effect with ion migration in perovskite solar cells. Sol. RRL 6, 2200050 (2022).
Bertoluzzi, L. et al. Mobile ion concentration measurement and open-access band diagram simulation platform for halide perovskite solar cells. Joule 4, 109–127 (2019).
Diekmann, J. et al. Determination of mobile ion densities in halide perovskites via low-frequency capacitance and charge extraction techniques. J. Phys. Chem. Lett. 14, 4200–4210 (2023).
Kniepert, J. et al. Reliability of charge carrier recombination data determined with charge extraction methods. J. Appl. Phys. 126, 205501 (2019).
Ghasemi, M. et al. A multiscale ion diffusion framework sheds light on the diffusion–stability–hysteresis nexus in metal halide perovskites. Nat. Mater. 22, 329–337 (2023).
Zu, F. et al. Position-locking of volatile reaction products by atmosphere and capping layers slows down photodecomposition of methylammonium lead triiodide perovskite. RSC Adv. 10, 17534–17542 (2020).
De Bastiani, M. et al. Toward stable monolithic perovskite/silicon tandem photovoltaics: a six-month outdoor performance study in a hot and humid climate. ACS Energy Lett. 6, 2944–2951 (2021).
Sahli, F. et al. Fully textured monolithic perovskite/silicon tandem solar cells with 25.2% power conversion efficiency. Nat. Mater. 17, 820–826 (2018).
Senocrate, A. et al. The nature of ion conduction in methylammonium lead iodide: a multimethod approach. Angew. Chem. Int. Ed. Engl. 56, 7755–7759 (2017).
Yoon, S. J., Kuno, M. & Kamat, P. V. Shift happens. how halide ion defects influence photoinduced segregation in mixed halide perovskites. ACS Energy Lett. 2, 1507–1514 (2017).
Onno, A., Chen, C. & Holman, Z. C. Electron and hole partial specific resistances: a framework to understand contacts to solar cells. in Proc. 46th IEEE Photovoltaic Specialists Conference (ed) 2329–2333 (IEEE, 2019).
Würfel, P. & Würfel, U. Physics of Solar Cells: From Basic Principles to Advanced Concepts (Wiley, 2009).
Kavadiya, S. et al. Investigation of the selectivity of carrier transport layers in wide-bandgap perovskite solar cells. Sol. RRL 5, 1–9 (2021).
Kang, D. H. & Park, N. G. On the current–voltage hysteresis in perovskite solar cells: dependence on perovskite composition and methods to remove hysteresis. Adv. Mater. 31, 1–23 (2019).
Jacobs, D. A. et al. The two faces of capacitance: new interpretations for electrical impedance measurements of perovskite solar cells and their relation to hysteresis. J. Appl. Phys. 124, 225702 (2018).
Pilania, G., Balachandran, P. V., Kim, C. & Lookman, T. Finding new perovskite halides via machine learning. Front. Mater. 3, 1–7 (2016).
Takahashi, K., Takahashi, L., Miyazato, I. & Tanaka, Y. Searching for hidden perovskite materials for photovoltaic systems by combining data science and first principle calculations. ACS Photonics 5, 771–775 (2018).
Li, J., Pradhan, B., Gaur, S. & Thomas, J. Predictions and strategies learned from machine learning to develop high-performing perovskite solar cells. Adv. Energy Mater. 9, 1901891 (2019).
Le Corre, V. M., Sherkar, T. S., Koopmans, M. & Koster, L. J. A. Identification of the dominant recombination process for perovskite solar cells based on machine learning. Cell Rep. Phys. Sci. 2, 100346 (2021).
Diekmann, J. et al. Pathways toward 30% efficient single‐junction perovskite solar cells and the role of mobile ions. Sol. RRL 5, 2100219 (2021).
Ion-induced field screening as a dominant factor in perovskite solar cell operational stability. Figshare https://figshare.com/s/cbfad738b0666ecf7f98 (2024).
Acknowledgements
We acknowledge HyPerCells (a joint graduate school of the University of Potsdam and the Helmholtz-Zentrum Berlin) and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—project numbers 423749265 and 424709669—SPP 2196 (SURPRISE-2 and HIPSTER-PRO), as well as project numbers 182087777-SFB951 and MUJUPO (RI 1551/12-2), for funding. K.B. and T.R. thank the DFG (HIPSTER-PRO:RI 1551/15-2), the BMBF (MOISTURE: 01DP20008 and the EU Horizon 2020 (FOXES: 951774) for funding. Y.W. acknowledges the National Natural Science Foundation of China (22179037). We also acknowledge financial support by the Federal Ministry for Economic Affairs and Energy within the framework of the 7th Energy Research Programme (P3T-HOPE, 03EE1017C). A.D. would like to thank the Penrose scholarship for generously funding his studentship. M.S. further acknowledges the Heisenberg programme from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) with project number 498155101 and the Vice-Chancellor Early Career Professorship Scheme from CUHK for funding. F.L. acknowledges funding by the Volkswagen Foundation via the Freigeist Program. A.A. acknowledges support from the Welsh Government’s Sêr Cymru II Rising Star through the European Regional Development Fund, Welsh European Funding Office and Swansea University Strategic Initiative in Sustainable Advanced Materials.
Funding
Open access funding provided by Universität Potsdam.
Author information
Authors and Affiliations
Contributions
J.T. and Sa.Sh. performed experiments, data analysis and contributed to drafting of the manuscript. E.G.-P., F.Z., F.P.-C, St.Ze., F.Y, M.S., P.C., A.D., F.A.A., Se.Se. and Sh.Zh. performed additional experiments. J.T., Sa.Sh., M.S, J.D. and K.P.P. performed simulations and provided programming support. K.O.B., J.W., Q.J., F.L., S.A., T.R., A.A., D.N., N.K., Y.W., V.M.L.C. and H.S. helped with the interpretation and analysis of the results. F.L., S.A., T.R., A.A., D.N., N.K., Y.W., H.S. and M.S. supervised students. M.S. initiated the research and drafted the manuscript.
Corresponding author
Ethics declarations
Competing interests
H.J.S. is co-founder and CSO of Oxford PV Ltd., a company commercializing perovskite PV technology. M.S., F.L. and D.N. are co-founders of FastChar UG, a company specializing in automated tools for perovskite solar cell characterization. The remaining authors declare no competing interests.
Peer review
Peer review information
Nature Energy thanks Carsten Deibel and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs 1–32, Table 1 and Notes 1 and 2.
Supplementary Data 1
Individual measurements for Supplementary Fig. 19.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thiesbrummel, J., Shah, S., Gutierrez-Partida, E. et al. Ion-induced field screening as a dominant factor in perovskite solar cell operational stability. Nat Energy 9, 664–676 (2024). https://doi.org/10.1038/s41560-024-01487-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41560-024-01487-w
This article is cited by
-
More ions in, less power out
Nature Energy (2024)