Large exomoons unlikely around Kepler-1625 b and Kepler-1708 b

Abstract

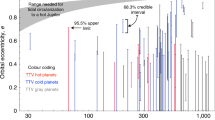
There are more than 200 moons in our Solar System, but their relatively small radii make similarly sized extrasolar moons very hard to detect with current instruments. The best exomoon candidates so far are two nearly Neptune-sized bodies orbiting the Jupiter-sized transiting exoplanets Kepler-1625 b and Kepler-1708 b, but their existence has been contested. Here we reanalyse the Hubble and Kepler data used to identify the two exomoon candidates employing nested sampling and Bayesian inference techniques coupled with a fully automated photodynamical transit model. We find that the evidence for the Kepler-1625 b exomoon candidate comes almost entirely from the shallowness of one transit observed with Hubble. We interpret this as a fitting artefact in which a moon transit is used to compensate for the unconstrained stellar limb darkening. We also find much lower statistical evidence for the exomoon candidate around Kepler-1708 b than previously reported. We suggest that visual evidence of the claimed exomoon transits is corrupted by stellar activity in the Kepler light curve. Our injection-retrieval experiments of simulated transits in the original Kepler data reveal false positive rates of 10.9% and 1.6% for Kepler-1625 b and Kepler-1708 b, respectively. Moreover, genuine transit signals of large exomoons would tend to exhibit much higher Bayesian evidence than these two claims. We conclude that neither Kepler-1625 b nor Kepler-1708 b are likely to be orbited by a large exomoon.

Main

From the discovery of Jupiter’s four principal moons in 1610 by Galileo Galilei¹, which triggered the Copernican revolution, to the discovery of cryovolcanism on Saturn’s moon Enceladus² as evidence of continuing liquid water-based chemistry in the outer Solar System, moons continue to deliver fundamental and fascinating insights into planetary science. The detection of moons around some of the thousands of extrasolar planets known today has, thus, been eagerly anticipated for over a decade now^3,4,5.

Although more than a dozen methods have been proposed to search for exomoons⁶, the search for moons in stellar photometry of transiting planets is the only method that has been applied by several research teams^7,8,9,10,11. The most promising search technique seems to be photodynamical modelling^12,13, which maximizes the signal-to-noise ratio (S/N) of any exomoon transit that might be present¹⁴. No exomoon has been securely detected so far, and the main reason for this is probably that moons larger than Earth are rare^10,15. For comparison, the largest moons in the Solar System, Ganymede (around Jupiter) and Titan (around Saturn), have radii of about 40% of the radius of the Earth. Exomoons of this size are below the detection limits even in the high-accuracy space-based photometry from the Kepler mission.

So far, two possible exomoon detections have been put forward, both of which had originally been claimed in stellar photometry from the Kepler space mission¹⁶. The first candidate corresponds to a Neptune-sized moon in a wide orbit around the Jupiter-sized planet Kepler-1625 b (ref. ¹⁵), which is in a 287 d orbit around the evolved solar-type star Kepler-1625. The second exomoon claim has recently been announced by the same team. It is around the Jupiter-sized planet Kepler-1708 b (ref. ¹⁷), which is in a 737 d orbit around the solar-type main-sequence star Kepler-1708.

Given the importance of possible extrasolar moon discoveries for the field of extrasolar planets and planetary science in general, those proposed candidates call for an independent analysis. Photodynamical modelling of planet–moon transits is computationally very demanding due to the three-body nature of the star–planet–moon system and due to the complicated calculations involved in the overlapping areas of three circles¹⁸. Although some open-source computer code packages cover some combination of Keplerian orbital motion solvers and multi-body occultations^19,20, they have not been adapted for studying exomoons. Another recently published algorithm²¹ has been used to study a peculiar planet–planet mutual transit of Kepler-51 b and d.

Here we apply our new photodynamical model Pandora¹³, a publicly available open-source code written in the Python programming language, to investigate the exomoon claims around Kepler-1625 b and Kepler-1708 b. The main differences between Pandora and LUNA, photodynamical software that has previously been used for exomoon searches, are (1) Pandora’s assumption of the small-body approximation of the planet whenever the resulting flux error is <1 ppm, (2) the different treatment of the three circle intersections of the star, planet and moon, (3) a different sampling of the posterior space (MultiNest for LUNA^15,22; UltraNest for Pandora), (4) a different conversion scheme between time stamps in the light curve and the true anomalies of the circumstellar and local planet–moon orbits and (5) an accelerated model throughput of Pandora of about 4 to 5 orders of magnitude¹³, while still keeping the overall flux errors <1 ppm.

Results

Kepler-1625 b

Using the data from the three transits observed with Kepler, we first masked one transit duration’s worth of data to either side of the actual transit before detrending. We found this amount of data to correspond roughly to the planetary Hill sphere, which we omit from the detrending to avoid the removal of any potential exomoon transit signature. We then explored three different approaches for detrending and fitting the Kepler data from stellar and systematic activity and combining it with Hubble data (Methods). The posterior sampling was achieved using the UltraNest software²³.

Approach 1 resulted in $2\log_\mathrm{e}({B}_{\rm{mp}})=15.9$, where B_mp is the Bayes factor for the planet–moon hypothesis over the planet-only hypothesis (Methods), signifying ‘decisive evidence’ for an exomoon according to the Jeffreys scale (Supplementary Table 1). In approach 2, the statistical evidence turned out to be about an order of magnitude lower in terms of B_mp, with $2\log_\mathrm{e}({B}_{\rm{mp}})=11.2$. In approach 3, the Bayesian evidence for an exomoon was almost yet another order of magnitude lower with $2\log_\mathrm{e}({B}_{\rm{mp}})=7.3$, which signifies ‘very strong evidence’. These results confirm the strong dependence of the statistical evidence of the exomoon-like signal on the detrending.

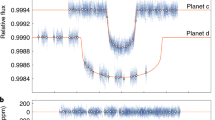
Figure 1a–d shows 100 light curves for the combined fit of the Kepler and Hubble data based on approach 2 (orange lines) that were randomly chosen from the posterior distribution. We do not show any planet-only models from the corresponding posteriors since the weighting of the number of planet–moon models and the number of planet-only models is based on the likelihood of the models (Methods) and the planet-only interpretation is 265 times less probable than the planet–moon interpretation. We do, nevertheless, show the best fit of the planet-only model in Fig. 1a–d for comparison (black solid line), which is important to our interpretation of the transit depth.

Fig. 1: Transit light curves of Kepler-1625 b.

Each column shows data for one of the four transits (transits 1 to 3 from Kepler and transit 4 from Hubble), respectively. The out-of-Hill-sphere parts of the Kepler-1625 b transit light curves were detrended using a sum of cosines, and the LDCs were used as free fitting parameters. Time is in units of BKJD, which is equal to BJD − 2,454,833.0 d. a–d Orange lines visualize 100 planet–moon models that were randomly drawn from the respective posterior distributions for transit 1 (a), transit 2 (b), transit 3 (c) and transit 4 (d). Planet-only models are omitted as the corresponding Bayes factor of $2\log_\mathrm{e}({B}_{\rm{mp}})=11.2$ suggests that the planet–moon interpretation is 265 times more probable than the planet-only interpretation. The best-fitting models of a planet only and of a planet with a moon are shown with solid and dashed black lines, respectively. Grey horizontal lines labelled as ‘Kepler mean’ illustrate the mean transit depth resulting from the three transits observed with Kepler. e–h Residuals of the observed data and the best fit of the planet-only model for transit 1 (e), transit 2 (f), transit 3 (g) and transit 4 (h). Red lines denote the five-bin walking mean. i–l Residuals of the observed data and the best fit of the planet–moon model for transit 1 (i), transit 2 (j), transit 3 (k) and transit 4 (l).

Plausibility of transit solutions

Although the statistical evidence is overwhelming, we noticed several things about the astrophysical plausibility of the solutions and the morphology of the transit light curves in Fig. 1a–d that put the statistically favoured planet–moon interpretation into question.

• (1) About half of the posterior models do not exhibit a single moon transit in any of the four transit epochs. This is particularly relevant since our posterior sampling with UltraNest is very conservative in its representation of the final posteriors to ensure that these posteriors are fair representations of the estimated likelihoods. The non-detection of any moon transits is not an exclusion criterion for the moon hypothesis, but it violates an important detection criterion for an exomoon interpretation²⁴.

• (2) In the other half of our posterior models that do contain moon transits, these transits occur almost exclusively in the Kepler data. This tendency for missed putative moon transits in the Hubble data has not been explicitly addressed in the literature and gives us pause to reflect on the fact that of a total of four available transits, this missed exomoon transit occurs in the one dataset that was obtained with a telescope (Hubble), unlike the remaining three transits (from Kepler).

• (3) From these posterior cases with a moon transit, we find only a handful of light curves with a notable out-of-planetary-transit signal from the moon (Fig. 1a–c). Instead, preferred solutions feature a moon with a small apparent deflection from the planet. This lack of solutions with moon transits at wide orbital deflections is contrary to geometrical arguments for a real exomoon. Any exomoon would spend most of its orbit in an apparently wide separation from its host planet as a result of the projection of the moon orbit onto the celestial plane^25,26. From our best fits of the orbital elements for the planet–moon models and using previously published equations for the contamination of planet–moon transits¹⁴, we calculate a probability of <10% that such a hypothetical exomoon around Kepler-1625 b would transit nearly synchronously with its planet during all three transits observed with Kepler. We interpret this as an artificial correction for the unconstrained stellar limb darkening, in which the ingress and egress of the moon transits are used in the fitting process to minimize the discrepancy between the data and the models.

• (4) The exomoon signal is almost entirely caused by the data from the Hubble observations although our model sampling of the posteriors prefers solutions in which the moon does not actually transit the star in the Hubble data. We did not find any evidence of a putative exomoon signal at 3,223.3 d (BKJD) in the Hubble data (Fig. 1d) as originally claimed²⁷. Our finding is, thus, in agreement with another study²⁸, though these authors analysed solely the Hubble data and not the Kepler data in a common framework.

• (5) The transit observed with Hubble is much shallower than the three transits observed with Kepler (Fig. 1a–d). Our bootstrapping experiment (Methods) yields a probability of 2 × 10⁻⁵ that the fourth transit from Hubble would have the observed transit depth, assuming the same astrophysical conditions and similar noise properties. The discrepancy can be explained as either an extrasolar moon that transits in all three transits observed with Kepler but misses the star in the single transit observed with Hubble or a wavelength dependency of the stellar limb darkening due to the different wavelength bands covered by the Kepler and Hubble instruments. Assuming only a planet and no moon as well as our best-fitting estimates for the planet-to-star radii ratio, transit impact parameter and limb-darkening coefficients (LDCs) for Kepler and Hubble, then we predict a transit depth of 0.99573 for the Kepler data and of 0.99634 for the Hubble data (Methods). These values are in good agreement with the observed transit depth discrepancy and offer a natural explanation that does not require a moon.

• (6) We confirm the previously reported transit timing variation (TTV) of the planet. Our best planet-only fit for the transit midpoint of Kepler-1625 b at 3,222.55568 (±0.0038) d is consistent with the published value of 3,222.5547 (±0.0014) d (ref. ²⁹) with a deviation of much less than the standard deviation (σ). The TTV has a discrepancy of about 3σ of the predicted transit mid-time at 3,222.6059 (±0.0182) d using the three transits from Kepler alone. It is unclear if this timing offset was caused by a moon, by an additional, yet otherwise undetected planet around Kepler-1625 (refs. ^27,29,30) or by an unknown systematic effect. Curiously, even if we artificially correct for this TTV, the exomoon solution is still preferred over the planet-only solution with similar evidence and similar posteriors. This suggests that not the TTV but the transit depth discrepancy between the Kepler and the Hubble data is the key driver of the statistical evidence for an exomoon around Kepler-1625 b. In other words, although the TTV between the Kepler and the Hubble data is statistically at the 3σ level and even though the exomoon interpretation around Kepler-1625 b hinges fundamentally on the Hubble data, the TTV effect is not as important. It is the transit depth discrepancy that causes the spurious moon signal.

• (7) The residual sum of squares in the combined Kepler and Hubble datasets, on a timescale of a few days, is 301.5 ppm² for the planet-only best fit (Fig. 1e–h) and 295.2 ppm² for the best-fitting planet–moon model (Fig. 1i–l). The root mean square (r.m.s.) is 625.7 ppm for the planet-only model and 619.1 ppm for the planet–moon model, respectively. The difference in r.m.s. between the models is very slim, only 6.6 ppm. Possibly more important, this metric for the noise amplitude is larger than the depth of the claimed moon signal of about 500 ppm (ref. ²²).

• (8) Our properly phase-folded exomoon transit light curve has a marginal S/N of only 3.4 or 3.0, depending on the detrending. There is also no visual evidence for an exomoon transit in this phase-folded light curve of Kepler-1625 b (Methods).

Transit injection-retrieval experiment

In addition to our exomoon search around Kepler-1625 b, we performed an injection-retrieval experiment using the original out-of-transit Kepler data of the star (Methods).

We tested 128 planet-only systems with planetary properties akin to those of Kepler-1625 b, and we tested two families of planet–moon models, each comprising 64 simulated systems. For both simulated exomoon families, we used physical planet–moon properties corresponding to our best fit from approach 2. For one exomoon family, we tested orbital alignments like those from our best fits, whereas for the other family we tested only coplanar orbits. Moons from the coplanar family would always show transits and possibly even planet–moon eclipses, thereby increasing the statistical significance. Orbital periods for all planet–moon systems ranged between 1 and 20 d.

The resulting distribution of the $2\log_\mathrm{e}({B}_{\rm{mp}})$ values as a function of the moon’s orbital period is shown in Fig. 2a. As a general observation, the Bayesian evidence increases substantially for moons in wider orbits, partly because more of the moon’s in-transit data are separated from the planetary in-transit data¹⁴. As an interesting side result, this is direct evidence from photodynamical modelling that a selection effect due to exomoon transit contamination by the planet will prefer exomoon discoveries in wide orbits. The Bayes factors for our own exomoon search around Kepler-1625 b (black filled circles) and those from previous works²⁷ (empty square) are several orders of magnitude lower than those from our injection-retrieval experiments with injected moons.

Fig. 2: Injection-retrieval tests of a planet-only model and two types of large moons into the out-of-transit data of the original light curve of Kepler-1625 b.

a, Bayes factor distribution for orbital periods of the injected moons between 1 and 20 d. Black open circles refer to injections of planet-only models with a random spread over the planet–moon period axis. Orange points refer to injections of a Kepler-1625 b-like planet and a moon that we parameterized according to the best-fitting posteriors of our own search. Blue dots with crosses show the outcome of simulations with a hypothetical coplanar system of a Kepler-1625-like planet with a large moon. The black solid circles and the black open square are the Bayes factors in this work and from ref. ²⁷ (see the legend). The dashed lines in the lower right corner outside the plotting area denote the boundaries of the Jeffreys grades for $2\log_\mathrm{e}({B}_{\rm{mp}})$ of 0, 2.30, 4.61, 6.91 and 9.21, respectively. b, Bayes factor histograms for the two types of injections with moons. Colours correspond to the same moon types as in a.

Our retrievals demonstrate that our detrending does not, in the most cases, erase an exomoon signal that would be present in the Kepler data. Our true positive rate, defined as decisive evidence on the Jeffreys scale ($2\log_\mathrm{e}({B}_{\rm{mp}}) > 9.21$), is between 76.6% and 96.9%, depending on the orbital geometry of the injected planet–moon system. Details are given in Supplementary Table 4. For injected moons with periods near 20 d, we find $2\log_\mathrm{e}({B}_{\rm{mp}})$ ranging between 100 and 1,800. The real Kepler plus Hubble data suggests $2\log_\mathrm{e}({B}_{\rm{mp}})$ between 7.3 (this work, detrending approach 3) and 25.9 (ref. ²⁷). At the corresponding moon orbital periods of 17 to 24.5 d, these $2\log_\mathrm{e}({B}_{\rm{mp}})$ values are more compatible with our injection-retrievals of a planet-only model (black open circles). Figure 2b illustrates the same data as a $2\log_\mathrm{e}({B}_{\rm{mp}})$ histogram, highlighting that by far most of our injected exomoons have $2\log_\mathrm{e}({B}_{\rm{mp}})$ values larger than those found for the real transit data of Kepler-1625 b. Importantly, in 14 out of 128 simulated planet-only transits, we find $2\log_\mathrm{e}({B}_{\rm{mp}}) > 9.21$, corresponding to a false positive rate of 10.9%.

Kepler-1708 b

For the two transits of Kepler-1708 b, we tested the same three detrending and fitting approaches as for Kepler-1625 b. Each of these approaches resulted in distinct Bayes factors when comparing the planet-only and the planet–moon models (Supplementary Table 3). None of the resulting Bayes factors suggests strong evidence in favour of an exomoon interpretation. With approach 1, we obtain $2\log_\mathrm{e}({B}_{{{{\rm{mp}}}}})=-4.0$, that is to say, a 1/0.14 = 7.1-fold statistical preference for the planet-only hypothesis. Approach 2 yields $2\log_\mathrm{e}({B}_{\rm{mp}})=1.0$, which is a statistical hint of an exomoon and ‘not worth more than a bare mention’ on the Jeffreys scale³¹. And with approach 3, we obtain $2\log_\mathrm{e}({B}_{\rm{mp}})=2.8$, which is substantial evidence of an exomoon around Kepler-1708 b. Details of the posterior sampling and best-fitting model solutions are given in the Methods.

Figure 3a,b shows a random selection of planet-only (blue) and planet–moon (orange) transit light curves from our posterior sampling with UltraNest. This particular set of solutions was obtained with detrending approach 2. In our graphical representations, we chose to show both planet–moon solutions and planet-only solutions by weighting the number of light curves per model with the corresponding Bayes factor. In this particular case, we plot n_p = 1/(1 + B_mp) = 67% of the light curves based on planet-only models and n_mp = 1 − 0.5 = 33% with planet–moon models (Methods).

Fig. 3: Transit light curves of Kepler-1708 b.

The out-of-Hill-sphere parts of the Kepler-1708 b transit light curves were detrended using a biweight filter and the LDCs were used as free fitting parameters. a,b, Blue and orange lines visualize 67 planet-only models and 33 planet–moon models, respectively, that were randomly drawn from the respective posterior distributions for transit 1 (a) and transit 2 (b). The number of light curves represents the corresponding Bayes factor B_mp = 0.5, which means that the planet-only interpretation is twice as probable as the planet–moon interpretation. The best-fitting models of a planet only and of a planet with a moon are shown with dashed and solid black lines, respectively. c,d, Residuals of the observed data and the best fit of the planet-only model for transit 1 (c) and transit 2 (d). Red lines denote the five-bin walking mean. e,f, Residuals of the observed data and the best fit of the planet–moon model for transit 1 (e) and transit 2 (f). ppt, parts per thousand.

Plausibility of transit solutions

We identify several aspects that are critical to the assessment of the plausibility of the exomoon hypothesis.

• (1) It has been argued that the pre-ingress dip of transit 1 between about 771.6 and 771.8 d (BKJD) cannot be caused by a star spot crossing of the planet since the planet is not in front of the star at this point¹⁷. We second that, but we also point out that at 1,508 d (BKJD), just about 1 d before transit 2, there was a substantial decrease in the apparent stellar brightness of ~800 ppm (see residuals in Fig. 3d,f) that is as deep as the suspected moon signal. This second dip near 1,508 d (BKJD) also cannot possibly be related to a star spot crossing, which demonstrates that astrophysical or systematic variability may also explain the pre-ingress dip of transit 1 of Kepler-1708 b. An exomoon is not necessary for explaining the pre-ingress variation of transit 1.

• (2) The residual sum of squares for the entire data in Fig. 3 is 108.4 ppm² for the planet-only best fit and 107.7 ppm² for the best-fitting planet–moon model. The r.m.s. is 529.9 ppm for the best-fitting planet-only model and 528.2 ppm for the best planet–moon model. For comparison, the depth of the proposed moon transit is ~1,000 ppm and several features in the light curve have amplitudes of ~800 ppm on a timescale of 0.5 d. The proposed exomoon transit signal is not distinct from other sources of variations in the light curve, which are probably of stellar or systematic origin.

• (3) Although we identify visually apparent dips that could be attributed to a transiting exomoon, other variations in the phase-folded light curve that cannot possibly be related to a moon cast doubt on the exomoon hypothesis (Methods).

• (4) Most of the claimed photometric moon signal occurs during the two transits of the planetary body, which makes it extremely challenging to discern the exomoon interpretation from limb-darkening effects related to the planetary transit. This finding is reminiscent of our analysis of the transits of Kepler-1625 b. Due to geometrical considerations it is, in fact, unlikely a priori that a moon performs its own transit in a close apparent deflection to its planet.

• (5) Our orbital solutions for the proposed exomoon vary substantially depending on the detrending method. As an example, the orbital period of the moon obtained from our best fits is 12.0 (±19.0), 1.6 (±5.6) or 7.2 (±6.2) d for detrending approaches 1, 2 and 3, respectively. We verified that these are not aliases on the same orbital mean motion frequency comb but rather completely independent solutions. For a real and solid exomoon detection, we would expect that the solution is stable against various reasonable detrending methods.

Transit injection-retrieval experiment

In the same manner as for Kepler-1625 b, we performed 128 planet-only injection-retrievals and two sorts of 64 planet–moon injection-retrievals, all with orbital periods between 1 and 20 d. For each injection, we used out-of-transit data from the original Kepler-1708 b light curve from the Kepler mission.

Figure 4a shows the $2\log_\mathrm{e}({B}_{\rm{mp}})$ distribution resulting from our injection-retrieval tests as a function of the injected orbital period of the moon. Injected moons and real measurements for Kepler-1708 b are colour-coded as in Fig. 2. The Bayes factors that we find for the injected moons indicate decisive Bayesian evidence ($2\log_\mathrm{e}({B}_{\rm{mp}}) > 9.21$) in over half of the cases and values up to ~100 when the orbital period of the planet–moon system P_pm > 10 d. We retrieved a true positive in 34 out of 64 cases (53.1%) with an injected moon like the best fit and in 38 of 64 cases (59.4%) with a coplanar injected moon (Methods). Figure 4b demonstrates that both our statistical evidence and the previously found evidence¹⁷ are clearly separated from about 2/3 of the population of retrieved exomoons with injected parameters drawn from the 2σ intervals of our best-fitting moon model of Kepler-1708 b. The Bayes factors of the best-fitting planet–moon and planet-only models for the real transits of Kepler-1708 b are close to the distribution of the Bayes factors of our injected planet-only models. Our false positive rate among the planet-only injections with decisive evidence is 2/128 = 1.6% (Methods and Supplementary Table 5).

Fig. 4: Injection-retrieval tests of a planet-only model and two types of large moons into the out-of-transit data of the original light curve of Kepler-1708.

a, Bayes factor distribution for orbital periods of the injected moons between 1 and 20 d. Black open circles refer to injections of planet-only models with a random spread over the planet–moon period axis. Orange points refer to simulations with a Kepler-1708 b-like planet and a moon that we parameterized according to the best-fitting posteriors of our own search. Blue dots with crosses show the outcome of injections of a hypothetical coplanar system with a Kepler-1708-like planet and a large moon. The black solid and black open circles with error bars refer to the Bayes factors of this work and of ref. ¹⁷ (see legend). The dashed lines in the lower right corner outside the plotting area denote the boundaries of the Jeffreys grades for $2\log_\mathrm{e}({B}_{\rm{mp}})$ of 0, 2.30, 4.61, 6.91 and 9.21, respectively. b, Bayes factor histograms for the two types of injections with moons. Colours correspond to the same moon types as in a.

Discussion

Our unified approach for detecting exomoon transits in stellar photometry includes statistical measures, plausibility checks of the obtained solutions, visual inspection of stellar light curves and careful interpretation of the posterior samplings. This results in the following interpretation of the two exomoon candidates around Kepler-1625 b and Kepler-1708 b.

Exomoon candidate around Kepler-1625 b

The Bayesian evidence in favour of a large exomoon around Kepler-1625 b depends strongly on the choice of the detrending method. Although we find ‘very strong’ to ‘decisive’ evidence ($7.3\lesssim 2\log_\mathrm{e}({B}_{\rm{mp}})\lesssim 15.9$), some new arguments lead us to conclude that Kepler-1625 b is not orbited by a large exomoon (Results).

Another aspect that has not been addressed explicitly before is the truncated out-of-transit baseline of the Hubble data. This has a crucial effect on the shape and the depth of the transit. The incomplete detrending necessarily leads to a mis-normalization and possibly even to the injection of false positive exomoon signals³². In combination with the perils induced by the wavelength dependence of the stellar limb darkening, we think that the Hubble data of the Kepler-1625 b transit are, therefore, not useful for an exomoon search.

In addition to the excessive statistical analysis of the light curve of Kepler-1625 b and our inspection of the noise properties of the Kepler and Hubble light curves, there is no visual evidence of any moon transit in the data. Although this is not a decisive argument against an exomoon, since visual inspection is not an ideal tool for identifying transits nor for rejecting transits, a clear transit signal would be something that everybody would like to see for a first detection of an exomoon. In this case, the extraordinary claim of an exomoon around the giant planet Kepler-1625 b is not supported by any visual evidence in the data of an exomoon transit.

Exomoon candidate around Kepler-1708 b

The Bayesian evidence for the proposed exomoon around Kepler-1708 b is weaker than that for Kepler-1625 b, ranging between a support of the planet-only hypothesis and substantial evidence for an exomoon ($-4\lesssim 2\log_\mathrm{e}({B}_{\rm{mp}})\lesssim 2.8$), depending on the light curve detrending. Whichever detrending we use, we obtain consistently lower evidence for the exomoon hypothesis than the 11.9-fold preference over the planet-only hypothesis ($2\log_\mathrm{e}({B}_{\rm{mp}})=4.95$) as previously claimed¹⁷. We attribute part of this disagreement to our use of the UltraNest software when sampling the posterior space. Previous studies used MultiNest, which may produce biased results³³ and underestimated uncertainties³⁴, both of which are avoided with UltraNest²³. Beyond our Bayesian analysis, our close inspection of the transit light curve reveals several arguments that can explain the data without the need for an exomoon (Results).

Our injection-retrieval experiments using real out-of-transit Kepler data of Kepler-1708 show that an exomoon with similar physical properties as the previously claimed exomoon would have a much higher Bayes factor ($10\lesssim 2\log_\mathrm{e}({B}_{\rm{mp}})\lesssim 100$) than suggested by the actual data. Although this finding in itself does not mean that there is not a real exomoon in the original Kepler-1708 b data, it makes us suspicious that of all the possible transit realizations for a given exomoon around Kepler-1708 b, Kepler observed two transits in which the Bayesian evidence of an exomoon is barely above the noise level.

Finally, the false positive rate of 1.6% of our injection-retrieval tests suggests that an exomoon survey in a sufficiently large sample of transiting exoplanets with similar S/N characteristics yields a large probability of at least one false positive detection, which we think is what happened with Kepler-1708 b (Methods).

Exomoon detection limits

We executed additional injection-retrieval experiments to get a more general idea of exomoon detectability with current technology. Photodynamical analyses of our simulated light curves with idealized space-based exoplanet transit photometry suggests that exomoons smaller than about 0.7 R_⊕ or closer than about 30% Hill radii to their gas giant host planets cannot possibly be detected with Kepler-like data. For comparison, the largest natural satellite of the Solar System, Ganymede, has a radius of about 0.41 R_⊕, and all the principal moons of the Solar System gas giant planets are closer than about 3.5% of their planetary host’s Hill sphere.

Thus, any possible exomoon detection in the archival Kepler data or with upcoming PLATO observations will necessarily be odd when compared to the Solar System moons. In this sense, the now refuted claims of Neptune- or super-Earth-sized exomoons around Kepler-1625 b and Kepler-1708 b could nevertheless foreshadow the first genuine exomoon discoveries that may lay ahead.

Methods

Model parameterization

Our planet-only model has seven fitting parameters for Kepler-1708 b and nine fitting parameters for Kepler-1625 b. For both systems, we used the circumstellar orbital period of the planet (P_p), the orbital semimajor axis (a_p), the planet-to-star radii ratio (r_p), the planetary transit impact parameter (b_p), the time of the first planetary mid-transit (t_0,p) and two LDCs for the quadratic limb-darkening law to describe the limb darkening in the Kepler band (u_1,K, u_2,K). For Kepler-1625 b, we also require two additional LDCs to capture the limb darkening in the Hubble band (u_1,HST, u_2,HST).

It is important to note the methodological difference to the model used in the previous study that claimed a Neptune-sized exomoon around Kepler-1625 b (ref. ²⁷). That model also included a parameter to fit for any possible radius discrepancy between the Kepler and the Hubble data. Taking one step back, there are two possible reasons for a transit depth discrepancy in two different instrumental filters, for example from Kepler and Hubble. First, the planet can actually have different apparent radii in different wavelength bands, for example caused by a substantial atmosphere with wavelength-dependent opacity³⁵. Second, the wavelength dependence of stellar limb darkening can lead to different shapes and different maximum flux losses during the transit, even for a planet without an atmosphere³⁶. The first aspect of the wavelength dependence of the planetary radius was covered for Kepler-1625 b in the first study that analysed the combined Kepler plus Hubble data in the search for an exomoon²⁷. These authors found that the radii ratio of the planet in the Hubble and the Kepler data was ~1, with a standard deviation of about 1%. This result can be retrieved from their Table 2 (second parameter R_p,HST/R_p,Kep) and from their Fig. S16 (parameter p_H/p_K). The largest discrepancy is found with their quadratic detrending method, which yields R_p,HST/R_p,Kep = 1.009 (+0.019, −0.017). The upper limit within 1σ is 1.009 + 0.019 = 1.028. Our best fit for the planet-to-star radii ratio is 0.0581 (±0.0004), depending on the detrending method. To achieve a radius discrepancy of 1.028, our planet-to-star radii ratio would need to be about 0.0597/0.0581 ≈ 1.028 between the Kepler and the Hubble data, which is 4σ away from our best fit. We are, thus, sufficiently confident that we can drop the wavelength dependence of the planetary radius in our fitting procedure. As for the second aspect of the wavelength dependence of stellar limb darkening, this astrophysical phenomenon naturally reproduces the observed transit depth discrepancy plus the difference in the transit profiles, all at one go. This can be seen by comparing Fig. 1a–c with Fig. 1d, in which the transit in the Hubble data is fitted well with two different pairs of LDCs and without the need for a wavelength dependence of the planetary radius. All things combined, a planetary radius dependence on wavelength is not required. Instead, the wavelength dependence of stellar limb darkening can naturally explain the different transit shapes and transit depths between the Kepler and the Hubble data. This difference in our model parameterization leads to different solutions for the posteriors compared to the previous study²⁷.

Our planet–moon model includes a total of 15 fitting parameters for Kepler-1708 b: the stellar radius (R_s), two stellar LDCs to parameterize the quadratic limb-darkening law (u_1,K, u_2,K), the circumstellar orbital period of the planet–moon barycentre (P_b), the time of inferior conjunction of the first mid-transit of the planet–moon barycentre (t_0,b), the orbital semimajor axis of the planet–moon barycentre (a_b), the transit impact parameter of the planet–moon barycentre (b_b), the planet-to-star radii ratio (r_p), the planetary mass (M_p), the moon-to-star radii ratio (r_m), the orbital period of the planet–moon system (P_pm), the inclination of the planet–moon orbit against the circumstellar orbital plane (i_pm), the longitude of the ascending node of the planet–moon orbit (Ω_pm), the orbital phase of the moon at the time of barycentric mid-transit (τ_pm) and the mass of the moon (M_m). For Kepler-1625 b, we required another two LDCs for the Hubble data (u_1,HST, u_2,HST), making a total of 17 fitting parameters in this case. In principle, Pandora can also model eccentric orbits, which would add another four fitting parameters (for details see ref. ¹³), but we focused on circular orbits in this study. All times are given as barycentric Kepler Julian day (BKJD), which is equal to barycentric Julian day (BJD) − 2,454,833.0 d.

As our priors for the star Kepler-1625 (KIC 4760478), we used a stellar mass of ${M}_{{{{\rm{s}}}}}=1.11{3}_{-0.076}^{+0.101}\,{M}_{\odot }$ (subscript ⊙ refers to solar values), a radius of ${R}_{{{{\rm{s}}}}}=1.73{9}_{-0.161}^{+0.143}\,{R}_{\odot }$ and an effective temperature of ${T}_{{{{\rm{eff}}}}}=5,54{2}_{-132}^{+155}$ K, as derived from isochrone fitting³⁷. For the star Kepler-1708 (KIC 7906827), we used as our priors ${M}_{{{{\rm{s}}}}}=1.06{1}_{-0.079}^{+0.073}\,{M}_{\odot }$, ${R}_{{{{\rm{s}}}}}=1.14{1}_{-0.066}^{+0.073}\,{R}_{\odot }$ and ${T}_{{{{\rm{eff}}}}}=5,97{2}_{-122}^{+126}$ K (ref. ³⁷).

In one of our approaches to fitting the data with Pandora, we fixed the stellar LDCs to study the effect of stellar limb darkening on the posterior distribution and the evidence of any exomoon signal. For Kepler-1625 b, we used two sets of LDCs. In the band of Hubble’s Wide Field Camera 3, we used the same LDCs as a previous study²⁸ (u_1,HST = 0.216 and u_2,HST = 0.183), the values of which were derived from PHOENIX stellar atmosphere models³⁸ for a main-sequence star with an effective temperature of T_eff = 5,700 K and with solar metallicity, [Fe/H] = 0. To ensure consistency between the fixed LDCs in the Kepler and Hubble passbands, we derived the LDCs in the Kepler band from pre-computed tables³⁹, again based on PHOENIX stellar atmosphere models for a star with T_eff = 5,700 K, [Fe/H] = 0 and a surface gravity of $\log (g/[{{{\rm{cm}}}}\,{{{{\rm{s}}}}}^{-2}])=4.5$, for which (u_1,K = 0.482 and u_2,K = 0.184).

Although t_0,p is the time of the first planetary mid-transit in our model parameterization, UltraNest requires a prior (T₀), which we took from the literature. For Kepler-1625 b, we used T₀ = 636.210 d (ref. ²⁷), and for Kepler-1708 b, we used T₀ = 772.193 d (ref. ¹⁷; all times in BKJD). We restricted the UltraNest search for t₀ to within ±0.1 d around the prior. This yielded ${t}_{0}={T}_{0}+0.0{1}_{-0.01}^{+0.01}$ for the planet-only model of Kepler-1625 b and ${t}_{0}={T}_{0}+0.0{1}_{-0.02}^{+0.02}$ for the barycentre of the planet–moon model of Kepler-1625 b. For Kepler-1708 b, we obtained ${t}_{0}={T}_{0}-0.0{1}_{-0.00}^{+0.00}$ for the planet-only model and ${t}_{0}={T}_{0}-0.0{1}_{-0.01}^{+0.01}$ for the barycentre of the planet–moon model.

The remaining planetary and orbital priors were drawn from uniform distributions.

Light curve detrending

Detrending has been shown to have a major effect on the statistical evidence for exomoon-like signals in transit light curves²⁷. Detrending can even inject artificial exomoon-like false positive signals in real data³². Moreover, a solid case for an exomoon claim should be robust against different detrending methods. Hence, we consider the detrending part of our data analysis as a crucial step and test three different approaches.

In all three detrending approaches, our Pandora model included two stellar LDCs for the Kepler data and an independent set of two LDCs for the Hubble data, both sets of which were used to parameterize the quadratic stellar limb-darkening law.

In detrending approach 1, we fixed the four LDCs based on stellar atmosphere model calculations³⁹. The detrending of the Kepler data was done using a sum of cosines as implemented in the Wōtan software⁴⁰, which is a re-implementation of the CoFiAM algorithm²⁴ that has previously been used to detect exomoon-like transit signals around Kepler-1625 b and Kepler-1708 b.

In approach 2, we explored the effect of treating the LDCs as either fixed or as free fitting parameters. We also used a sum of cosines for detrending as in approach 1, but the two sets of two LDCs were treated as free parameters during the fitting process.

In approach 3, we also used the four LDCs as free parameters but used the biweight filter implemented in Wōtan. The biweight filter has become quite a popular algorithm for detrending stellar light curves in search of exoplanet transits since it has the highest recovery rates for transits injected into simulated noisy data⁴⁰. Hence, we consider Tukey’s biweight algorithm also a natural choice for detrending when searching for exomoon transits.

Of course, more detrending methods could be explored, for example polynomial fitting³² and linear, quadratic or exponential fitting²⁷. As demonstrated for detrending light curves when searching for exoplanet transits⁴⁰, an optimal detrending function that works best in every particular case may not exist for exomoons either. Hence, we restrict our study to three detrending approaches that we found to perform exquisitely in our injection-retrieval experiments, as they have low false positive and false negative rates as well as high true positive and true negative rates.

Supplementary Fig. 1 (for Kepler-1625 b) shows the resulting posterior sampling from UltraNest for detrending approach 2, as it produces the highest Bayes factor in favour of an exomoon signature. Moreover, in Supplementary Fig. 2 (for Kepler-1708 b), we illustrate the UltraNest posteriors after detrending with approach 3 for the same reason. The posterior samplings for the other two approaches appear qualitatively similar, although the exact values differ. We decided to present the maximum likelihood values and their respective standard deviations for each parameter in the column titles of these corner plots. These maximum likelihood values are different from the values that we list in Supplementary Table 2 (for Kepler-1625 b) and Supplementary Table 3 (for Kepler-1708 b), which present the mean values and standard deviations of the posterior samplings. We opted for these two different representations of the results between the corner plots and tables to give different perspectives of the non-Gaussian and often multimodal posterior samplings.

Bayesian evidence from nested sampling

We use the Bayes factor as our principal statistical measure to compare the planet-only and planet–moon models. The Bayes factor is defined as the ratio of the marginalized likelihoods of two different models. The marginal likelihood can be viewed as the integral over the posterior density ∫dθL(D∣θ)π(θ), where L(D∣θ) is the likelihood function and π(θ) is the prior probability density. We define the marginal likelihood of the transit model including a moon as Z_m and the marginal likelihood of the planet-only transit model as Z_p. In our work, the natural logarithm of the Bayesian evidence $\log_\mathrm{e}(Z)$ is computed numerically for both models (and given the respective data) using UltraNest²³. Then the corresponding Bayes factor is

$${B}_{\rm{mp}}=\frac{{Z}_{\rm{m}}}{{Z}_{\rm{p}}}=\frac{\exp \{{\log}_{\mathrm{e}}({Z}_{\rm{m}})\}}{\exp \{{\log}_{\mathrm{e}}({Z}_{\rm{p}})\}}=\exp \{{\log}_{\mathrm{e}}({Z}_{\rm{m}})-{\log}_{\mathrm{e}}({Z}_{\rm{p}})\},$$

(1)

where the $\log_\mathrm{e}$ function refers to the natural logarithm, that is, the logarithm to base e (Euler’s number). In the context of previous exomoon searches, the Bayes factor (B) has often been quoted on a logarithmic scale as $\log_\mathrm{e}(B)$ (ref. ¹⁵) or $2\log_\mathrm{e}(B)$ (ref. ²⁷). On this scale, a preference for the planet-only (planet–moon) model is indicated by negative (positive) values.

The Jeffreys scale³¹ has become widely used as a tool in astrophysics to translate numerical Bayes factors into spoken language. It has also been used in a modified form⁴¹ for previous estimates of the evidence for exomoons around Kepler-1625 b (ref. ²⁷) and Kepler-1708 b (ref. ¹⁷). Although the Jeffreys scale originally referred to the evidence against the null hypothesis (Z₀), we adopt the equivalent perspective of the evidence in favour of the alternative hypothesis (Z₁), in our case the evidence for an exomoon. Hence, we use the inverse numerical values for the Bayesian factor as discussed in the appendix of Jeffreys’ work³¹. In our terminology, B₁₀ = Z₁/Z₀ is the Bayes factor designating the evidence in favour of Z₁ over Z₀. Our adaption of the Jeffreys scale is shown in Supplementary Table 1, which also presents the corresponding values of $2\log_\mathrm{e}({B}_{10})$ as well as the odds ratio in favour of the alternative hypothesis (Z₁).

In representing the light curves that are randomly drawn from the posterior samples of UltraNest, we plot both planet–moon and planet-only solutions by taking into account the corresponding Bayes factor. We require that the ratio between the number of light curves with a moon (n_mp) and the number of light curves based on a planet-only model (n_p) is equal to the ratio of the corresponding marginalized likelihoods, n_mp/n_p = B_mp. Moreover, the sum of the ratios must be n_mp + n_p = 1. Substitution of n_mp yields n_pB_mp + n_p = 1, which is equivalent to n_p = 1/(1 + B_mp).

We utilize this conversion between the Bayes factor and the odds ratio of the evidences under investigation in equation (1) and contextualize it as a means to assess the deviation of a particular B measurement from the normal distribution of B measurements, assuming that the noise is normally distributed. This evaluation is done using the error function ${{{\rm{erf}}}}(x)=2/\sqrt{\pi }\int\nolimits_{0}^{x}\mathrm{d}t\operatorname{e}^{-{t}^{2}}$, which we compute numerically using erf(), which is a built-in Python function in the scipy library. Given a deviation of n times the standard deviation (σ) from the mean value of a normal distribution, the value of ${{{\rm{erf}}}}(n/\sqrt{2})$ gives the fraction of the area under the normalized Gaussian curve that is within the error bars. In particular, for n = 1, one obtains the well-known ${{{\rm{erf}}}}(1/\sqrt{2})=66.8$%.

The odds can then be calculated as $O=1/(1-{{{\rm{erf}}}}(n/\sqrt{2}))$, and with equation (1), we have $\log_e (B)=\log_e (O)$. Then a 3σ detection is signified by $\log_e (B)\,\ge \,5.91$, a 4σ detection by $\log_e (B)\,\ge \,9.67$ and a 5σ detection by $\log_e (B)\,\ge \,14.37$ (Supplementary Fig. 3). These numbers are in agreement with the results from previous 200 injection-and-retrieval tests¹⁷. From their sample of planet-only injections into the out-of-transit Kepler light curve of Kepler-1708 b, these authors found one false positive exomoon detection with ${\log }_{e}(B) > 5.91$. For comparison, we found that the odds for such a 3σ detection are 1/370, and so for 200 retrievals with an injected planet-only model, we would expect 200/370 = 0.54 false positives, which is 1 when rounded to the next full integer.

Convergence of nested sampling

For nested sampling, we used UltraNest with a multimodal ellipsoidal region and region slice sampling. The Mahalanobis measure is used to define the distance between the start and end points of our walkers. The strategy terminates as soon as the measure exceeds the mean distance between pairs of live points. Specifically, UltraNest integrates until the live point weights are insignificant (<0.01). In different experiments, we used static and dynamic sampling strategies with 800 to 4,000 active walkers and always required 4,000 points in each island of the posterior distribution before a sample was considered independent. All experiments yielded virtually identical results, showing excellent robustness. In addition, we performed 1,000 injection-retrieval experiments to ensure that the recovery pipeline was robust.

Likelihood surface exploration is sufficiently complete after about 10⁸ model evaluations for our data (Supplementary Fig. 4), whereas approximately 10⁹ model evaluations yielded only marginal gains. Many other sampling strategies, such as reactive nested sampling or the use of correlated model parameters, led to slower convergence by up to three orders of magnitude. Moreover, the MultiNest software previously used for planet-only and planet–moon model evaluations of the transit light curves of Kepler-1625 b and Kepler-1708 b has been shown to yield biased results³³ and to systematically underestimate uncertainties in the best fit parameters³⁴. These two key problems of MultiNest are avoided in UltraNest²³. Our corresponding UltraNest sampling of the models generated with Pandora took 14 hr on a single core of an AMD Ryzen 5950X processor.

With regards to our UltraNest fits of Kepler-1625 b, detrending approach 1 resulted in more than 2.5 × 10⁸ planet–moon model evaluations, approach 2 in over 1.3 × 10⁹ planet–moon model evaluations and approach 3 in almost 2.3 × 10⁸ planet–moon model evaluations. For the UltraNest sampling of the Kepler-1708 b data after detrending with approaches 1, 2 and 3, we generated 1.6 × 10⁸, 2.3 × 10⁸ and 1.7 × 10⁸ planet–moon model evaluations, respectively.

For comparison, a typical nested sampling of 5 × 10⁸ model evaluations (Supplementary Fig. 4) takes 9 h on a single 4.8 GHz core of an Intel Core i7-1185G7 at a typical speed of 15,000 model evaluations per second.

Exomoon detectability

In view of the now several exomoon candidate claims near the detection limit, the general question about exomoon detectability in space-based stellar photometry arises. Due to the high computational demands of exoplanet–exomoon fitting^12,13, this question cannot be addressed in an all-embracing manner for all possible transit surveys, cadences, system parameters, etc. Nevertheless, we executed a limited and idealized injection-retrieval experiment to determine the smallest possible moons that are detectable in Kepler-like data of (hypothetical) photometrically quiescent stars.

All stars exhibit intrinsic photometric variability, which is caused by magnetically induced star spots, p-mode oscillations, granulation and other astrophysical processes. Moreover, any observation—even high-accuracy space-based photometry—comes with instrumental noise components from the readout of the charged coupled devices (CCDs), long-term telescope drift, short-term jitter, intra-pixel non-uniformity, charge diffusion, loss of the CCD quantum efficiency etc. After modelling and removing the instrumental effects, the photometrically most quiet stars with a Kepler magnitude Kp < 12.5 from the Kepler mission have been shown to exhibit a combined differential photometric precision over 6.5 h of about 20 ppm (ref. ⁴²). Given that the nominal long cadence of the Kepler mission is 29.4 min and that the S/N scales with the square root of the number of data points, this corresponds to an amplitude of 72 ppm per data point, although great care should be taken when interpreting the combined differential photometric precision as a measure of stellar activity⁴².

In our pursuit to identify the idealized scenarios in which exomoons can be found, that is to say, to identify the smallest exomoons possible, we consider a nominal Neptune-sized planet in a 60 d orbit around a Sun-like star, corresponding to a semimajor axis of 0.3 AU. To some extent, we have in mind the most abundant population of warm mini-Neptune exoplanets that this hypothetical planet could represent. Over 2, 3 and 4 yr, such a planet would make 12, 18 and 24 transits, respectively. We also envision an exomoon around this planet, for which we test different physical radii and orbital periods around the planet. In the following, we find it helpful to refer to the extent of the moon orbit in units of the Hill radius (${R}_{{{{\rm{Hill}}}}}={a}_{{{{\rm{b}}}}}{({M}_{{{{\rm{p}}}}}/[3{M}_{{{{\rm{s}}}}}])}^{1/3}$), which can be considered as a sphere of the gravitational dominance of the planet. Moons in a prograde orbital motion, which orbit the planet in the same sense of rotation as the direction of the planetary spin, become gravitationally unbound beyond ~0.4895 R_Hill (ref. ⁴³). Retrograde moons, for comparison, can be gravitationally bound even with semimajor axes up to ~0.9309 R_Hill (ref. ⁴³), depending on the orbital eccentricity. For comparison, the Galilean moons reside within 0.8% and 3.5% of Jupiter’s Hill radius, Titan sits at 1.8% of Saturn’s Hill radius and Triton orbits at 0.3% of Neptune’s Hill radius. The Earth’s Moon has an orbital semimajor axis of about 0.26 R_Hill.

In our experiment, we test exomoon injections throughout the entire Hill radius, which corresponds to an orbital period of about 33 d. For all our simulations, we used the Pandora software¹³ to generate planet–moon transit models at 30 min cadence to which we added normally distributed white noise as described. For each test case, we simulated a total of 18 transits over a nominal mission duration of 3 yr, representative of a Kepler-like space mission. The upcoming PLATO mission, for example, will observe two long-observation phase fields for either 2 + 2 yr or for 3 + 1 yr, respectively, in the hunt for Earth-like planets around Sun-like stars^44,45. We then used the UltraNest software to populate the posteriors in the parameter space of both the planet-only and the planet–moon models and computed the Bayes factors, as in the main part of this study for Kepler-1625 b and Kepler-1708 b. The whole exercise was then repeated for moon orbital periods between 1 and 33 d and moon radii between 0.5 R_⊕ and 1.0 R_⊕. We define an exomoon recovery as an UltraNest detection of the injected signal with $2\log_{\rm{e}}({B}_{\rm{mp}}) > 9.21$, corresponding to decisive evidence on the Jeffreys scale.

Supplementary Fig. 5a shows one simulated transit of our hypothetical warm Neptune-sized exoplanet and its Earth-sized moon around a Sun-like star in the white noise limit as described. The moon transit is barely visible by the human eye and is statistically insignificant. After 18 transits, however, the transit becomes statistically significant and is even detectable in the phase-folded light curve of the planet–moon barycentre as the orbital sampling effect^25,26 (Supplementary Fig. 5b). Supplementary Fig. 6 shows the distribution of our recoveries in the parameter plane spanned by the moon radius and the moon’s orbital semimajor axis in units of R_Hill. As a main result, we find that moons smaller than about 0.7 R_⊕ are barely detectable even for these idealized cases with completely inactive stars and a total of 18 transits for a given planet–moon system. Moreover, the recovery rate drops to zero for orbits closer than about 0.3 R_Hill, which corresponds to orbital periods <5.5 d. This latter finding is in line with recent findings for the preservation of the exomoon in-transit signal being favoured in wide exomoon orbits¹⁴.

Injection-retrieval tests

The purpose of our injection-retrieval experiments for the observational data of Kepler-1625 b and Kepler-1708 b is twofold. First, we wanted to control the ability of our detrending approach to preserve any exomoon transit signal in those cases in which an exomoon is, indeed, present in the data. Second, we wanted to quantify the probability that our detrending approach induces a false exomoon signal in those cases in which no injected exomoon transit is actually present.

Our experiment began with the preparation of light curve segments that contain only stellar plus instrumental and systematic effects but no known planetary transits or possible moon transits. We removed the known planetary transits as well as 2 d segments before and after each planetary mid-transit time. For each injection of a planet–moon transit with Pandora, a random time in the remaining Kepler light curve was chosen. We then extracted a segment of 5 d around each injected mid-transit time for further use and validated that no more than five data points were missing to avoid using gaps in our experiment.

In the next step, we created synthetic models with Pandora. These were either planet-only models or models with planet–moon systems. As for the planet-only injections, for both Kepler-1625 b and Kepler-1708, we performed a total of 128 exomoon searches in the light curve segments that contained only a planetary transit injection, with planetary properties drawn from our planet-only solutions for Kepler-1625 b or Kepler-1708 b, respectively. We chose negligible moon masses and radii, and the planet–moon orbital periods were chosen successively between 1 and 20 d with a constant step size of (20 − 1) d/128 = 0.148375 d. Strictly speaking, the choice of these periods is irrelevant since no moons were effectively injected in the planet-only data, but this arrangement of the data simplified the use with Pandora and it aided the representation of the $2\log_\mathrm{e}({B}_{\rm{mp}})$ distribution from the planet-only injections in Figs. 2 and 4.

As for the exomoon injections, we distinguished two sorts of exomoons. For each type, there were 64 simulations on a grid of orbital periods between 1 and 20 d and a constant step size of (20 − 1) d/64 = 0.0297 d. For both Kepler-1625 b and Kepler-1708 b, we assumed one scenario of a moon in a coplanar orbit, that is to say, with i_pm = 0° and Ω_pm = 0°, but with randomized orbital phase offsets (τ_m). This set-up ensured that there were moon transits during every planetary transit and that planet–moon eclipses occurred occasionally, a scenario that should increase the statistical signal of the moon. In a second scenario, we injected a planet and moon with the same radii and orbital distance but now i_pm and Ω_pm were drawn randomly from within the 2σ confidence interval of our posterior distributions obtained using detrending approach 2. This scenario is representative of the best-fitting exomoon solutions for Kepler-1625 b and Kepler-1708 b and helped us to assess the true positive and false negative rates of our real exomoon search in the actually observed transits.

We injected these synthetic models in independent runs. In each run, a randomly chosen Kepler data segment was multiplied by the synthetic signal. Then the stellar and instrumental noise was detrended using Wōtan’s implementation of Tukey’s biweight filter⁴⁰ with a window size of three times the planetary transit duration while masking the actual planetary transit before calculating the trend.

Finally, we ran UltraNest twice for each injected transit sequence, once with a planet–moon model and once with a planet-only model. The Bayes factor was then calculated in the form $2\log_\mathrm{e}({B}_{\rm{mp}})$.

Injection-retrieval for Kepler-1625 b

The statistics of the original exomoon claim around Kepler-1625 b (ref. ¹⁵) was determined using the LUNA photodynamical model code¹² together with MultiNest sampling⁴⁶ in a Bayesian framework. This resulted in $2\log_\mathrm{e}({B}_{\rm{pm}})=20.4$ and an interpretation of ‘strong evidence’ of an exomoon according to the Kass and Raftery scale⁴¹. During their investigations of the Hubble follow-up observations, the authors re-examined the Kepler data and noticed a substantial decrease of the Bayes factor to $2\log_\mathrm{e}({B}_{\rm{pm}})=1$, which means that the evidence for an exomoon was essentially gone in the Kepler data.

The reason was found in an update of the Kepler Science Processing Pipeline of the Kepler Science Operations Center (SOC) from v.9.0 to v.9.3. Although the initial exomoon claim study¹⁵ used data from SOC pipeline v.9.0, the subsequent study²⁷ used Kepler data from SOC pipeline v.9.3. The previous exomoon claim has now been explained as being a mere systematic effect in the Kepler data. Ironically, when adding the new transit data from Hubble observations, a new exomoon-like signal was found with $2\log_\mathrm{e}({B}_{\rm{pm}})=11.2$ or $2\log_\mathrm{e}({B}_{\rm{pm}})=25.9$, depending on the method used for detrending the out-of-transit light curve. The claimed moon was now in a very wide orbit at ~40 planetary radii from the planet and with an orbital period of ${P}_{{{{\rm{pm}}}}}\,=\,2{2}_{-9}^{+17}$ d, although the posterior distribution of P_pm was highly multimodal²⁷.

Previous studies²² also describe a transit depth of 500 ppm for an exomoon candidate around Kepler-1625 b in the Hubble data. Their authors argued that if this feature were due to star spots rather than due to an exomoon, the depth of the signal should be about 650 ppm in the Kepler data, given the different bandpass response functions of Kepler and Hubble. They fitted box-like transit models to 100,000 out-of-transit regions of the Kepler data of Kepler-1625 b and found that 3.8% of the experiments resulted in box-like transits deeper than 650 ppm (depth >650 ppm) and that 3.5% of the tests produced negative (inverted) transits with amplitudes below 650 ppm (depth <650 ppm).

Their injection-recovery tests of simulated data with only white noise resulted in similar though slightly smaller rates of such false positives with a similar symmetrical behaviour of positive and negative transits. The authors of these previous studies concluded that the spurious detections in the real and simulated Kepler data are, thus, due to Gaussian (white) noise rather than to time-correlated noise from star spots or other periodic stellar activity.

Our own injection-retrieval experiments for Kepler-1625 b were not restricted to the assumption of white noise. Instead, we used transit-free light curve segments from the original Kepler data of Kepler-1625 as described above. We used the fourth transit from Hubble as is, as there was not enough out-of-transit Hubble data to inject and retrieve artificial transits and to do proper detrending for recovery.

Figure 2 shows the results of our injection-retrieval tests for Kepler-1625 b. Of the 128 injections of planet-only models (black circles), 96 are scattered between $2\log_\mathrm{e}({B}_{\rm{mp}})=-0.13$ and −7.49. With 114 systems showing a Bayes factor lower than our decisive detection limit of $2\log_\mathrm{e}({B}_{\rm{mp}})=9.21$, we determine a true negative rate of 89.1% and a false positive rate of 10.9%.

Of our 64 simulated planet–moon systems that were parameterized according to our UltraNest posteriors (orange dots), 61 (95.3%) showed $2\log_\mathrm{e}({B}_{\rm{mp}}) > 15.9$. More generally, we retrieved 62/64 = 96.9% of all moons with $2\log_\mathrm{e}({B}_{\rm{mp}}) > 9.21$, 59 of which even had $2\log_\mathrm{e}({B}_{\rm{mp}}) > 100$.

From the injected transit models that included a moon on a coplanar orbit (pale blue dots with crosses), 45 (70.3%) had $2\log_\mathrm{e}({B}_{\rm{mp}}) > 15.9$, as obtained with our detrending approach 1 of the original Kepler data. We also measured a true positive rate ($2\log_\mathrm{e}({B}_{\rm{mp}}) > 9.21$) of 49/64 = 76.6%, of which 29 successful retrievals signified $2\log_\mathrm{e}({B}_{\rm{mp}}) > 100$.

Injection-retrieval for Kepler-1708 b

The exomoon claim paper for Kepler-1708 b proposes a super-Earth-sized moon with a radius of ${R}_{{{{\rm{m}}}}}=2.6{1}_{-0.43}^{+0.42}\,{R}_{\oplus }$ at a distance of $11.{7}_{-2.2}^{+3.9}\,{R}_{{{{\rm{p}}}}}$ and with an orbital period of ${P}_{{{{\rm{pm}}}}}=4.{6}_{-1.8}^{+3.1}$ d. The authors of that paper calculated a Bayes factor of B_mp = 11.9, which means $2\log_e ({B}_{{{{\rm{mp}}}}})=4.95$ (ref. ¹⁷) and ‘strong evidence’. The authors performed 200 injections of a planet-only signal, in which they found 40 systems with $2\log_e ({B}_{{{{\rm{mp}}}}}) > 0$ and two systems with $2\log_e ({B}_{{{{\rm{mp}}}}}) > 4.61$ (their Fig. 3, but note the abscissa scaling and the limit at $\log_e ({B}_{{{{\rm{mp}}}}}) > 2.3$).

Figure 4 presents the outcome of all these simulations. Black open circles represent the 128 planetary transit injections without a moon, the $2\log_\mathrm{e}({B}_{\rm{mp}})$ values of which are scattered between about −1.5 and −7.4. Orange points represent the exomoon–exoplanet injections that we sampled from the 2σ confidence interval of our best fit using detrending approach 2. Blue points with crosses refer to the coplanar exomoon–exoplanet injections. For comparison, we plotted the measurements for the proposed exomoon signal around Kepler-1708 b from previous work¹⁷ and from this work (Supplementary Table 3). In 22 of the 64 tests (34.4%) with an injected moon that was parameterized from the 2σ posteriors, we found $2\log_e ({B}_{{{{\rm{mp}}}}}) < 0$, that is, the moon signal was completely lost. In 39 out of 64 cases (60.9%), we found a $2\log ({B}_{{{{\rm{mp}}}}})$ value that is higher than the value of 2.8 that we derived by fitting the LDCs using a biweight filter. In 17 out of 64 cases (26.6%) with coplanar planet–moon orbits, we found $2\log_e ({B}_{{{{\rm{mp}}}}}) < 0$ and the moon signal was completely lost. In 44 out of 64 cases (68.8%), we recovered the injected moon that was parameterized akin to the candidate around Kepler-1708 b with a $2\log_e ({B}_{{{{\rm{mp}}}}})$ value larger than the value of 2.8 that we obtained by fitting LDCs and using a biweight filter for detrending.

In summary, the actual value of $2\log_e ({B}_{{{{\rm{mp}}}}})=2.8$ for the proposed exomoon candidate is rather small compared to the values that we typically obtain from our injection-retrieval tests. Whenever there is really a moon in the data, it can be found with higher confidence than the proposed candidate in most cases. The Bayes factor of the candidate in the real Kepler data is also suspiciously close to the distribution of systems for which there was actually no moon present (Fig. 4).

In two of our 128 cases that included only planetary transits, we obtained $2\log_e ({B}_{{{{\rm{mp}}}}}) > 9.21$. That is, our false negative rate was 1.6%. This value is compatible with the false positive rate of $1.{0}_{-1.0}^{+0.7}\, \%$ reported by ref. ¹⁷. This finding highlights an interesting aspect that goes beyond the detection of an exomoon claim around Kepler-1708 b. Our false positive rate is equivalent to a probability of (1 − 2/128)¹ = 98.4% that we do not detect a false positive exomoon in a Kepler-1708 b-like transit light curve. In two exomoon searches, the probability that we would not produce a single false positive would be (1 − 2/128)² = 96.9%. After n searches, the probability of not detecting a false positive would be (1 − 2/128)ⁿ, and after 70 attempts the probability of having no false positive is 33.2%. In turn, the probability of having at least one false positive after 70 exomoon searches is 1 − (1 − 2/128)⁷⁰ = 66.8%. Of course, this estimate is applicable only to stellar light curves with comparable stellar activity and noise characteristics. However, we find this an interesting side note given that the exomoon claim paper of Kepler-1708 b included a sample of 70 transiting planets¹⁷. From this perspective, the detection of a false positive giant exomoon around Kepler-1708 b is, maybe, not as surprising.

Phase-folded transit light curves

We artificially re-added the planetary contribution to the combined planet–moon transit, which is not just a simple addition of a single planetary transit model, due to the possible planet–moon eclipses, but requires careful modelling with our photodynamical exoplanet-exomoon transit simulator Pandora¹³. Supplementary Fig. 7 illustrates that there is no appealing visual evidence of an exomoon transit in the observations of Kepler-1625. The depth of the putative exomoon transit varies substantially between 500 ppm for approach 2 and 100 ppm for approach 3, but the S/N was also marginal at <3.4 or <3.0 for all four transits, depending on the detrending approach.

In both Supplementary Figs. 8a (detrending approach 2) and 8b (detrending approach 3), we see the folding of the two proposed exomoon transits around zero mid-transit time. However, we also see another dip of almost similar depth at about −1.5 d before the planetary mid-transit of transit 2 (orange dots), which corresponds to the dip at 1,508 d (BKJD) mentioned above in our discussion of Supplementary Fig. 3. So, for Kepler-1708 b there actually is a visual hint of a stellar flux decrease in addition to the transit of the planet. However, its proximity in the light curve to another substantial variation in the light curve casts a serious doubt on the exomoon nature of the stellar flux decrease.

Hence, neither in the phase-folded light curve of the barycentre of Kepler-1625 b and its proposed moon nor for that of Kepler-1708 b did we identify any visually apparent variation that could be exclusively explained by an exomoon transit.

Transit depth discrepancy of Kepler-1625 b

To assess the probability that the observed discrepancy for the transit depths of Kepler-1625 b in the Kepler and Hubble data could be due to a statistical variation, we executed a bootstrapping experiment. We simulated the three transits observed with Kepler based on our measurements of the mid-transit flux of 0.99571, 0.99566 and 0.99567, respectively, and with formal uncertainties of 0.0001. These mid-transit fluxes and the uncertainties were chosen as mean values and standard deviations from which we drew 10 million randomized samples for each of the three transits.

The resulting histogram is shown in Supplementary Fig. 9. The transit depth of transit 4 from Hubble is indicated with an arrow at 0.99610 with a formal uncertainty of roughly 30 ppm. From the total of 30 million realizations, we measured a fraction of 2 × 10⁻⁵ with a transit depth greater than or equal to the observed transit depth from Hubble. It is, thus, highly unlikely that the observed transit depth discrepancy in the Kepler versus the Hubble data is a statistical variation, assuming normally distributed errors. Instead, an astrophysical origin, red noise or an unknown cause are required as an explanation.

We advocate for an astrophysical explanation that is well known in stellar physics and that does not require an exomoon. The radial profile of the apparent stellar brightness (or stellar intensity), known as the stellar limb-darkening profile, depends on the wavelength band that a star is observed in. This effect was originally observed for the Sun⁴⁷. Limb-darkening profiles can be described well by ad hoc limb-darkening laws, for which we use a quadratic limb-darkening law that is parameterized by two LDCs. When the stellar transit of an extrasolar planet is observed in two different filters, then the resulting LDCs and transit depth can vary substantially³⁶, whereas the transit impact parameter and the planet-to-star radii ratio must, of course, be the same.

Assuming circular orbits, the mid-transit depth (δ) can be expressed in terms of the minimum in-transit flux (${f}_{\min }$) as $\delta =1-{f}_{\min }$, so that we can predict the minimum in-transit flux with ${f}_{\min }=1-\delta$ if we can predict δ. Using the expression of the transit depth as a function of the transit overshoot factor from the light curve (o_LC)³⁶ (equation (1) in this reference), we have

$$\delta =(1+{o}_{{{{\rm{LC}}}}}){\left(\frac{{R}_{{{{\rm{p}}}}}}{{R}_{{{{\rm{s}}}}}}\right)}^{2}\,.$$

(2)

Using equation (3) in ref. ³⁶ and our best-fitting estimates from the planet-only model with (R_p/R_s) = 0.05818, an impact parameter b_p = 0.11, and LDCs for Kepler (u_1,K = 0.42, u_2,K = 0.41) and Hubble (u_1,H = 0.12, u_2,H = 0.21), we predict a transit depth of 0.99573 for the Kepler data and of 0.99634 for the Hubble data. These values are in good agreement with the transit depth discrepancy that we actually observe (Fig. 1). The transit depth discrepancy between the Kepler and the Hubble data can, thus, be readily explained by the wavelength dependence of stellar limb darkening, and it does not require an exomoon.

Methodological comparison to previous studies of Kepler-1625 b

Although there has not been any follow-up study to test the exomoon claim around Kepler-1708 b, various papers have analysed the Kepler and Hubble transit data for Kepler-1625 b. Here we provide a brief historical summary of the debate around Kepler-1625 b and its proposed exomoon candidate and give an overview of the methodological differences between our study and previous studies.

The initial statistical decisive evidence of an exomoon with $2\log_\mathrm{e}({B}_{\rm{pm}})=20.4$ (B_pm) was based on three transits available in archival Kepler data from 2010 to 2013¹⁵. In a subsequent study²⁷, the authors noticed that the evidence of an exomoon in the Kepler data was gone ($2\log_\mathrm{e}({B}_{\rm{pm}})=1$), which they attributed to an update of the Kepler Science Processing Pipeline of the SOC from v.9.0 to v.9.3. The original exomoon claim around Kepler-1625 b has, thus, been explained as a systematic effect. A new exomoon claim was made by the same authors based on new observations of a fourth transit observed with the Hubble Space Telescope from 2017²⁷, with $2\log_\mathrm{e}({B}_{\rm{pm}})$ ranging between 11.2 and 25.9 for various detrending methods used for the light curve segments. Curiously, the Hubble observations showed a TTV compared to the strictly periodic transits from Kepler, which could in principle be caused by the gravitational pull of a giant moon on the planet. Reported TTVs range between 77.8 min (ref. ²⁷) and 73.728 (±2.016) min (ref. ²⁹). The strong dependence of the statistical evidence on the details of the data preparation has, however, questioned the exomoon interpretation around Kepler-1625 b (refs. ^28,29,32).

• (1) Our study applies the same software and the same kind of injection-retrieval test to the transits of both Kepler-1625 b and Kepler-1708 b in a unified framework.

• (2) refs. ^32,29 used a numerical scheme that was hardcoded specifically to the case of exoplanet–exomoon transit simulations for Kepler-1625 b. Their code is not public, and thus, it has been challenging for the community to reproduce their results.

• (3) refs. ^15,32 studied only the three transits from the Kepler mission because the follow-up transit observations with Hubble were not available at the time. In our study, we combine data from four transits from the Kepler and Hubble missions.

• (4) ref. ²⁸ studied only the single transit observed with Hubble but none of the three transits from the Kepler mission.

• (5) refs. ^15,32 used Kepler data from the Kepler SOC pipeline v.9.0. As first noted by ref. ²⁷, the previously claimed exomoon signal around Kepler-1625 b that was present in the Simple Aperture Photometry measurements in the discovery paper¹⁵ vanished after the upgrade of Kepler’s SOC pipeline to v.9.3. We use data from Kepler’s SOC pipeline v.9.3 in our new study. These new data have also been used by refs. ^27,29,22.

• (6) refs. ^29,32,28 used the differential Bayesian information criterion for the planet-only and the planet–moon models, whereas refs. ^15,27,22 used the Bayes factor. We also use the Bayes factor in our study.

• (7) refs. ^32,29 used Markov chain Monte Carlo sampling of the posterior distribution, which is prone to becoming trapped in local regions of the parameter space. refs. ^27,22 used the MultiNest software for the posterior sampling, which can introduce biases in the fitting process³³ and which underestimates the resulting best fit uncertainties³⁴. In contrast to all those previous studies, we used the UltraNest software for posterior sampling, which avoids these problems²³.

• (8) Only one previous study of the transit light curve of Kepler-1625 b featured injection-retrieval experiments²². The methods for the injection-retrieval experiment used in this previous study assumed box-like transits and were, thus, less realistic than those we applied. Moreover, we disagree with the conclusions of these authors about the occurrence rate of false positive exomoon-like transit signals in the Kepler data (Injection-retrieval for Kepler-1625 b).

Transit animations

For both Kepler-1625 b and Kepler-1708 b, we generated video animations of the best-fitting planet–moon solutions in the posterior distributions. These animations were generated with the Pandora software using the model parameterization for the maximum likelihood provided by our UltraNest sampling. At the times of the transit midpoints of the respective planet–moon barycentre, we exported a screenshot, the results of which are shown in Supplementary Fig. 10. The colours of the stars Kepler-1625 and Kepler-1708 were chosen automatically in Pandora to reflect the stellar colours as they would be perceived by the human eye, according to previously published digital colour codes of main-sequence stars⁴⁸. We increased the frame rate to five times its default value, which is one frame every 30 min or 48 frames per day. Our animations, thus, have 240 frames of simulated data per day and they are played at a rate of 60 frames per second.

As shown by the corresponding corner plots in Supplementary Figs. 1 and 2, the posterior distributions are very scattered and any moon solutions are ambiguous at best. As we have discussed in the main text, it is much more probable that there is no large exomoon around either planet. So the purpose of these animations is mostly a general illustration of planet–moon orbital dynamics during transits as well as an interpretation of the transit light curves (and potentially debugging) rather than to represent the actual transit events. If Pandora’s animation functionality were to be used to visualize actual transit events, then the posterior distributions would need to be much more well confined and the Bayes factors of the solutions would need to be much higher (and, thus, the solution more convincing) than for Kepler-1625 b or Kepler-1708 b.