Abstract
Despite its simplicity and relevance for the description of electronic correlations in solids, the Hubbard model is seldom inarguably realized in real materials. Here, we show that monolayer Nb3Cl8 is an ideal candidate to be described within a single-orbital Hubbard model, constructed within a “molecular” rather than atomic basis set using ab initio constrained random phase approximation calculations. We provide the necessary ingredients to connect experimental reality with ab initio material descriptions and correlated electron theory, which clarifies that monolayer Nb3Cl8 is a Mott insulator with a gap of about 1.4 to 2.0 eV depending on its dielectric environment. Comparisons to an atomistic three-orbital model show that the single-molecular-orbital description is adequate and reliable. We further comment on the electronic and magnetic structure of the compound and show that the Mott insulating state survives in the low-temperature bulk phases of the material featuring distinct experimentally verifiable characteristics.
Similar content being viewed by others
Introduction
The first theoretical studies of correlation effects in solids date back as early as 1934 with studies on the so-called polar model1. In this model, the crystal was represented as a periodic array of single-orbital sites such that each site can be empty, double occupied, or single occupied with a spin up or down electron, and various types of hopping and interaction processes were taken into account2,3. Further simplification resulted in the appearance of the Hubbard model4,5,6,7,8 in the 1960s, in which only basic processes of single-electron hopping and on-site Coulomb repulsion are taken into account. Although the Hamiltonian of this model is simple, the physics that emerges from the competition between interaction and kinetic hopping, or between localization and delocalization, is extremely rich and complicated. As a function of temperature, lattice structure, and number of electrons, the phase diagram of the model is believed to contain metallic and insulating phases, magnetic ordering, and more exotic phases such as unconventional superconductivity and charge-density waves9. In general, the model is too difficult to be solved exactly in the thermodynamic limit (except in one10 and infinite dimensions11,12), but many efficient computational strategies have been devised, and some regions of the phase space are well-understood nowadays9,13,14.
Given its theoretical importance and computational difficulty, experimental realizations of the Hubbard model have long been sought since then nature itself would solve the model for us. Some unconventional superconductors, including cuprates15,16 and nickelates17,18, as well as NaxCoO219 have been described using the single-orbital Hubbard model. However, in these cases, most simplified single-orbital models are controversial, and there are indications that multiorbital models are needed9. Single-orbital models seem to be, nevertheless, adequate to describe transition metal dichalcogenides undergoing charge-density-wave transitions, with one low-energy orbital per supercell20. Artificial lattices, in the form of ad-atoms on surfaces21,22 or atoms trapped in optical lattices23 are other prominent examples. However, an actual solid that features the ideal realization of Hubbard model physics in the unit cell is of course even more desired. There are several difficulties associated with finding such material. First of all, most materials have several bands relatively close to the Fermi level, which casts doubt on a single-orbital low-energy description. Secondly, background screening in the solid should be so efficient that the Coulomb interactions between electrons on different sites are effectively zero, which is unrealistic for many two-dimensional materials24. Thirdly, the Coulomb interaction between electrons on the same site should be strong enough to find the desired strong correlation effects.
The class of Nb3X825 with X being either Cl, Br, or I forms a promising basis for finding such a realization of the Hubbard model. While Nb3Br8 has been described as an “obstructed atomic insulator"26, Nb3Cl8 monolayer has been proposed as a suitable candidate for a true Hubbard material27,28. At the DFT level, it has a single well-isolated band crossing the Fermi level. At the same time, experimental angle-resolved photo emission observations27,29 and transport measurements30 show a gap in bulk structures, which could be an indication of strong correlation effects. However, until now, no first-principles calculations of the strength of the local and non-local Coulomb matrix elements have been performed. Here, we use the constrained Random Phase Approximation (cRPA)31 to calculate the relevant partially-screened Coulomb matrix elements and show that the local Hubbard interaction is indeed sufficient to open a Mott gap in the monolayer. Furthermore, by comparing models with three and one orbitals per unit cell, we demonstrate that the single-orbital model is indeed applicable. We provide all parameters, including interactions and hopping matrix elements, as necessary for many-body calculations of the material’s electronic properties and investigate the derived models on the level of the Hubbard-I approximation. Furthermore, we show that the bulk structure can also be described by a slightly more involved two-orbital Hubbard model and investigate it in various experimentally observed high- and low-temperature structures.
Results
The high-temperature lattice structure of Nb3Cl8 is shown in Fig. 1. In each van der Waals monolayer, the Nb atoms form a distorted kagome lattice, with small (red) and big (blue) triangles. The distortion is 16.6%, i.e., the sides of the small triangle are 16.6% shorter and those of the big triangle 16.6% longer than for an undistorted kagome lattice, in which both would be a/2 = 3.36 Å. The monolayer unit cell contains three Nb atoms, such that the unit cell can be chosen to contain exactly one complete small (red) triangle, which we refer to hereafter as a trimer. At low-temperature, further distortions take places32,33,34, reducing the symmetry, which we discuss together with the bulk structures in more detail below.
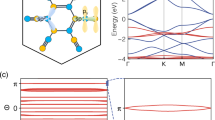
Figure 2a shows the monolayer electronic band structure at the DFT level, i.e., without considering strong electronic correlations. There are three Nb d (t2g) bands close to the Fermi level, of which one is crossing the Fermi level, while the other two are slightly above. At Γ these states can be described by their 2a1 and 2e symmetries, respectively27,32,33. Additional t2g and eg bands are above and below (green). Finally, a block of Cl p bands can be found below −2.7 eV (blue). A Wannier construction for the 2a1 and 2e t2g bands, see Methods, provides three equivalent orbitals ψ1,2,3 each localized at one of the three Nb atoms in the trimer, as shown in Fig. 2c–e. In each case, the orbital lobes have a particular orientation with respect to the triangle of atoms, as indicated in Fig. 2b.
a Shows DFT and Wannier-interpolated electronic structures without spin polarization. Bands in red, green, and blue colors stand for Nb-\({t}_{2g}^{1}\), Nb-\(({t}_{2g}^{2}+{e}_{g})\), and Cl p states, respectively. \({t}_{2g}^{1}\) orbitals are schematically illustrated in (b) for each Nb atom (in rotated coordinates), while \({t}_{2g}^{2}\) represents all other t2g orbitals. Opened and filled markers stand for the atomic (AO) and molecular (MO) orbital models, respectively. c–e Show Wannier atomic orbitals for each Nb atom, (f) their sum, and (g) the Wannier molecular orbital.
An isolated trimer with only internal hopping t0 > 0 between the three atomic Wannier orbitals has three single-particle states with energies −2t0 (2a1) and twice-degenerate t0 (2e) as obtained from diagonalization of the isolated trimer Hamiltonian. Then, adding a hopping t∥ ≪ t0 between trimers leads to one low-energy band and a pair of higher-energy bands, each with a bandwidth of order t∥ and a gap of 3t0. The strong distortion of the kagome lattice thus allows us to describe the 2a1 and 2e bands observed in Fig. 2a by a triangular lattice tight-binding model in a basis of molecular (trimer) orbitals.
For an isolated trimer, the lowest molecular orbital wave function is a symmetric combination \({\psi }_{0}=\frac{1}{\sqrt{3}}({\psi }_{1}+{\psi }_{2}+{\psi }_{3})\) of the atomic wave functions, as shown in Fig. 2f. Correspondingly, a Wannier construction for the lowest 2a1 band using only one orbital per trimer yields such a molecular orbital, as shown in Fig. 2g. This confirms that the trimer molecular orbital picture is a simple explanation of the low-energy single-particle electronic structure.
In Tables 1 and 2, we summarize the hopping parameters corresponding to the single molecular orbital (MO) and three-band atomic orbital (AO) Wannier constructions, respectively. The magnitudes of the hopping parameters are consistent with the picture of weakly hybridized trimers on a triangular lattice (see Methods for more details).
Coulomb interaction using constrained Random Phase Approximation
Having established two Wannier orbital basis sets, we study the correlation effects in Nb3Cl8 using the extended Hubbard model
where \({c}_{i\sigma }^{{\dagger} }\) and ciσ are fermionic creation and annihilation operators, respectively, creating or annihilating an electron in orbital i with spin σ; \({n}_{i\sigma }={c}_{i\sigma }^{{\dagger} }{c}_{i\sigma }\) is the spin-density operator for spin σ on orbital i. The Coulomb interaction matrix elements Uijkl (Ui = Uiiii and Uij = Uiijj) are evaluated within the Wannier orbital basis sets and using the constrained Random Phase Approximation (cRPA) scheme31(see Methods). To this end, the electronic structure is divided into a target space and a rest space. This approximation should be applicable when the rest space has a large gap35, and the two spaces can be disentangled cleanly. Here, the symmetry of the distorted kagome lattice greatly helps the disentanglement. Furthermore, the rest space has a gap of 2.5 and 2 eV for the AO and MO target spaces, respectively. This is sufficiently large compared to the bandwidths of the individual bands to have confidence in the cRPA accuracy. In this sense, Nb3Cl8 is an extraordinarily promising candidate for realizing a most simple Hubbard model.
In the present case, there are two relevant choices for the target space: all of the three lowest 2a1 and 2e states spanned by three atomic Nb d orbitals, or just the lowest metallic 2a1 band, best described by the lowest MO. We have performed cRPA calculations for both cases, and the resulting Coulomb matrix elements \({U}_{(ijkl)}^{(s)}\) are given in Tables 1 and 2 with s referring to the distance ("shells") and i, j, k, l to the atomic orbitals in the AO model. For the onsite R = 0 Coulomb interactions we find U(0) ≈ 1.9 eV in the MO model and \({U}_{0000}^{(0)}\approx 2.8\) eV (\({U}_{0011}^{(1)}\approx 1.8\) eV) in the atomic model. U(0) and \({U}_{0000}^{(0)}\) are obviously not identical. There are two origins for these differences, one purely geometrical and one physical. The MO is constructed as a linear combination of atomic orbitals, meaning the Coulomb tensor should also be transformed to a new basis involving all intra-trimer Coulomb matrix elements yielding \({U}^{(0)}\approx 1/3\,{U}_{0000}^{(0)}+2/3\,{U}_{0011}^{(1)}\) (see Methods). Given the numbers in Table 2, more than half of the molecular Coulomb interaction comes from the interatomic interaction U0011 within the trimer. The transformation to the MO reduces the Coulomb matrix element since the molecular Wannier orbital, as depicted in Fig. 2g, is more spread out than the individual atomic Wannier orbitals in Fig. 2c–e. In addition to this geometrical effect, the Coulomb interactions in the MO model are further reduced because of the additional screening provided by the two 2e bands that are integrated out.
Figure 4 shows additional information about the Coulomb interaction in the MO. Formally, the cRPA produces a frequency-dependent interaction31,36U(ω). In Nb3Cl8, the partially-screened Coulomb interaction is, however, well approximated as frequency-independent in the range ω ∈ [0, 10] eV, and only reaches the asymptotic, bare value around ω = 30 eV. This shows that retardation effects are unimportant at the relevant electronic energy scales36. Next to these weak retardation effects, we find significant non-local values U(R) for R > 0, as shown in Fig. 4b, depicting the 1/R tail of the static Coulomb interaction. This long-range tail of the Coulomb interaction is a result of the reduced screening in 2D and the effective dielectric cRPA screening. In contrast, a metallic screening would yield a conventional Yukawa potential. In this figure, we also show how the non-local interaction of the molecular orbital is affected by a dielectric encapsulation of the monolayer (see Methods for details on the calculations). From this, we see that in the extrapolated fully free-standing ε = 1 case U(0) ≈ 2 eV and U(1) ≈ 0.9 eV, which can be reduced by an environmental screening of ε = 10 to approximately 1.4 and 0.4 eV, respectively. U(R) is thus rather susceptible to the environment.
The low-energy physics of the system, in particular, the thermodynamics and charge neutral excitations such as spin fluctuations, can be described using a purely local Hubbard model24, with an effective local interaction U* = U(0) − U(1). This effective interaction U* is barely affected by the substrate screening as a result of similar screening effects for U(0) and U(1). This is illustrated in Fig. 4c, which shows that U*(ε) reduces from about 1.15 to only 1 eV upon increasing the environmental dielectric screening from ε = 1 to 10.
Electronic correlations
Solving the single-orbital triangular lattice Hubbard model is a formidable task37, which requires advanced computational techniques and is beyond the scope of this paper. Our model derivations result in consistent parameter sets summarized in Table 1, which should be used for such calculations. Nevertheless, inspecting these model parameters given by our Wannier construction and cRPA calculations, we observe that the Coulomb interaction is substantially larger than the bandwidth of the partially filled low-energy band, U/∣9t(1)∣ ≈ 10 for the molecular model. Thus, strong coupling techniques can be used to get a first impression of the correlation effects. The so-called Hubbard-I approximation, a multi-band generalization38 of the approach introduced by Hubbard6, was suggested as an adequate approximation by default in the narrow-band limit38,39 such that we will exploit it here (see Methods for details on the calculations).
In Fig. 5a and c, we show the spectral functions of the AO and MO models, i.e., with 3 and 1 orbitals per trimer, calculated using the Hubbard-I approximation, taking into account the intratrimer interactions only. For the MO model, we take into account U(0) only, while for the AO model, we include the full trimer-local Coulomb tensor \({U}_{ijkl}^{(s)}\) where i, j, k, l are restricted to nearest-neighbour Nb positions on a single trimer (s ≤ 1). We also show in Fig. 5d results for the MO model using U* = U(0) − U(1). In all cases, the interaction leads to a significant frequency dependence in the local Hubbard-I self-energy, which splits the partially filled 2a1 band into an upper and lower Hubbard band, with a gap given by the effective interaction strength acting on the lowest half-filled molecular orbital. In addition, we have projected the spectral functions of the AO model onto the trimer eigenstate ψ0 to show that this is indeed the low-energy state, see Fig. 5b. This comparison proves that the system is a Mott insulator in the Hubbard-I approximation, regardless of the model that is used. We also note that considering models with more than three orbitals that include bands close to the lower Hubbard band does not show any signs of a charge-transfer gap as discussed in Supplementary Note 1.
a Atomic three-orbital model (AO), (b) its projection to the lowest molecular-orbital, (c) molecular single-orbital model (MO), (d) MO model based on U*, and (e) cross-section of those spectral functions at one selected momentum. The chosen chemical potential constraints the occupation to one electron per trimer and aligns the upper Hubbard band.
Comparing the Mott gaps in the three models, we find noticeable differences. The U* model obviously has a smaller gap since the effective local interaction is reduced by the intertrimer interactions. This effect is not included in the approximate Hubbard-I treatment of the other models. We, however, note that the U* approach aims to describe the equilibrium correlation functions of the system40,41,42. Its applicability to high-energy spectral properties is questionable, as we discuss at hand from a small finite-size cluster in Supplementary Note 2. This discussion also suggests that the local U alone could describe the Mott gap of the full model with non-local Coulomb interactions reasonably well. Comparing the gaps in the AO and the MO models, we find a small reduction of the gap in the MO model. Both approaches differ in their diagrammatic content with regard to the two higher-energy trimer states, and an exact match is, therefore, not expected. The AO model in the Hubbard-I approximation contains purely intratrimer effects in an exact way. In contrast, the MO model contains both intra- and intertrimer screening effects, but only on the (c)RPA level, while the correlation effects are subsequently taken into account using Hubbard-I, i.e., intratrimer only. The quantitative similarity is a sign that the appearance of the gap is largely caused by intratrimer correlation physics. On the other hand, since the AO model starts with the three bands, it has additional spectral weight at higher energies. Figure 5 shows that this spectral weight predominantly remains in the tight-binding bands, with a limited amount of spectral weight transferred to localized excitations at higher energy.
Finally, in all cases, we observe a significant bandwidth renormalization in the lower and upper Hubbard bands compared to the non-interacting 2a1 bandwidth. This is a result of the frequency dependence of the dynamical self-energy and is in agreement with recently obtained angle-resolved photoemission spectra27, which we discuss further in detail in Supplementary Note 1.
Magnetic properties
Given the strong Coulomb repulsion and the filling of one electron per trimer, there is a tendency to form single \(S=\frac{1}{2}\) magnetic moments on every trimer. In this strong coupling limit, a simple estimate for the magnetic exchange interactions is given by the Hubbard-Stratonovich transformation \({J}^{(s)}=-2{({t}^{(s)})}^{2}/{U}^{* }\), and the resulting values are given in Table 2 up to the third nearest neighbours. Note that for magnetic properties, we expect U* to be the best approximation to effectively take nonlocal Coulomb interactions into account. Figure 6 shows possible magnetic structures based on these interactions, including a ferromagnetic, striped anti-ferromagnetic, and 120∘ anti-ferromagnetic ordering together with their energy densities of the exchange interaction given by \(E=-\frac{1}{2{N}_{i}}{\sum }_{s}\mathop{\sum }\nolimits_{ij}^{{N}_{i}{N}_{j}^{(s)}}{J}_{ij}^{(s)}{{{{\bf{S}}}}}_{i}\cdot {{{{\bf{S}}}}}_{j}\). Here, i = 1, ⋯ , Ni stands for the magnetic moments in the magnetic unit cell, and \(j\ne i=1,\cdots \,,{N}_{j}^{(s)}\) represent all neighbours within the same distance \(| {{{{\bf{r}}}}}_{ij}^{(s)}|\) characterized by shell index s. From these structures, the 120∘ anti-ferromagnetic structure has the lowest energy, suggesting it adequately represents the magnetic ground state.
Discussion
With the help of two down-folded minimal models, we established a Hubbard model description of Nb3Cl8 based on correlated trimers positioned on a triangular lattice and under the influence of intertrimer hopping as well as long-range Coulomb interactions. Based on these ab initio models, we showed that monolayer Nb3Cl8 in the high-temperature (HT) phase is a Mott insulator deep in the Mott regime as a result of the integer one-electron occupation of each trimer and the strong trimer-local Coulomb interactions relative to the small inter-trimer hopping. Below, we further show that this Mott behaviour also survives in the distorted low-temperature (LT) phases as well as within bulk stacks. Previous studies suggested using U ≈ 1 eV as an ad hoc choice together with a Wannierized single-band to describe the bulk electronic structure27,28. Our first-principles cRPA study shows that this value is reasonable if charge-neutral excitations are considered and the system is mapped onto an effective Hubbard model using the renormalized U* = U(0) − U(1)24, to effectively take the non-local Coulomb interaction into account. We find slightly larger values of U* ≈ 1.15 eV for an isolated monolayer, with a reduction towards 1 eV for monolayers in a dielectric environment43,44 (see Methods for details). On the other hand, U(0) is more adequate to describe charged excitations, such as involved in angle-resolved photoemission experiments, which ranges in cRPA from about 1.4 to 2 eV in monoloayer Nb3Cl8 depending on the dielectric environment.
Based on the effective single-band Hubbard model describing Nb3Cl8 ML, we furthermore showed that a 120∘-antiferromagnetic structure forms between the magnetic moments localized on each trimer at the ground state. It is important to emphasise here that U⋆ is relevant for the magnetic properties. And, since the intra- and intertrimer Coulomb interactions are both screened in approximately the same way, the effect of screening by the environment on the magnetic properties is negligible. On the other hand, for spectral properties and especially the Mott gap, the cRPA U(0) is a more reliable quantity, which significantly changes with substrate screening.
We further estimate the spin-orbit coupling to be a small perturbation with respect to the Coulomb interaction. In the distorted kagome crystal structure yielding the correlated trimer lattice, Nb is formally in an [Nb3]8+ state. As the atomic spin-orbit coupling of Nb2+ and Nb3+ is below 100 meV45 and thus significantly smaller than the local Coulomb of U0000 ≈ 2.8 eV, spin-orbit coupling can be treated as a perturbation to the Mott insulating state here and will not change qualitatively the drawn conclusions. In Supplementary Note 3, we further show that on the ab initio mean field LSDA+U level, the flat band (which forms the lower and upper Hubbard band in Hubbard-1) is not affected at all by the spin-orbit coupling, which we interpret as a result of the three-fold rotation-invariance of the MO. The interplay of spin-orbit coupling with the crystal field can lead however to subtleties in the magnetic anisotropy39.
In the bulk structure, the details of the stacking between the layers affect the electronic properties via interlayer hybridization. In the orthorhombic lattice structure of the HT phase, the correlated trimers in the different layers are laterally shifted as visualized in Fig. 7(a). The resulting DFT band structure is shown in Fig. 8(a). It is similar to the ML HT band structure with a doubled amount of bands, which are mildly affected by interlayer hybridization. We now find two half-filled bands around the Fermi level with finite dispersion in kz direction. The corresponding atomic and MO models now host 6 Nb d states and 2 MOs, respectively. All model parameters for the MO model are given in Table 3, and the visualizations of the corresponding Wannier functions are shown in Supplementary Fig. 4. The nearest-neighbour intra-layer hopping matrix element t∥ ≈ 25 meV of the corresponding MO model is similar to the one in the ML. The nearest-neighbour inter-layer hopping \({t}_{1,2}^{\perp }\approx -15\) to 17 meV is on a similar order, such that the inter-layer hybridization does not qualitatively change the small-band width character of the metallic bands around the Fermi level. The direction dependence of \({t}_{1,2}^{\perp }\) is a result of the Cl positions, one of which can be either above or below the trimer.
a At high temperature (HT, space group \(P\bar{3}m1\)) and (b) and (c) at low temperatures (LT, space groups C2/m and R3, respectively). The on-top views depict layer 1, layer 2, layer 1/layer 2, and layer 2/layer 1', respectively. Spheres in fade and bright colors (green and yellow) represent atoms (of Nb and Cl) in neighboring layers. Brown arrows indicate the interlayer couplings \({t}_{n}^{\perp }\) (n = 1, 2) between the nearest trimers. Numbers around trimers are distances between the nearest Nb atoms in each layer (in Å).
a DFT electronic structure and (b) interacting spectral functions obtained using the Hubbard-I approximation. The top, middle, and bottom panels represent results in \(P\bar{3}m1\) (HT phase), C2/m (LT phase), and R3 (LT phase) space groups, respectively. The electronic structures in (a) are weighted between Nb-\({t}_{2g}^{1}\) (in red), Nb-\({t}_{2g}^{2}\) (in green), and Nb-eg (in blue) states, respectively. The spectral functions in (b) stand for the atomic six-orbital model (first panels), molecular two-orbital model (second panels), and the cross-section of those spectral functions at one selected momentum (last panels). The insets show the first Brillouin zones and symmetry directions for each structure. Symmetry points M and K for LT structures are chosen to represent the same in-plane directions as in the HT case.
Next to the kinetic parts of the model Hamiltonian, the Coulomb interaction matrix elements are also affected by the bulk structure due to enhanced screening. In the MO model, the local Coulomb interaction on each trimer is reduced from U ≈ 1.9 eV in the ML to U ≈ 1.5 eV in the bulk structure. Similar trends hold for the long-range interactions within the individual layers. Additionally, there are now inter-layer Coulomb matrix elements, of which only the density-density ones are of non-vanishing magnitude. In the MO model, these are ca. 360 meV. Given the half-filled flat bands and still significant trimer-local Coulomb interaction matrix elements, it is thus reasonable to expect that the Mott behaviour in the HT bulk phase survives. The corresponding results, taking only trimer-local interaction terms into account, are presented in Fig. 8 for both models. In the atomistic model, we find a Mott gap of about 1.6 eV, and in the MO model of about 1.5 eV.
For low temperatures, below 100 K, bulk Nb3Cl8 is known to undergo a structural phase transition supposedly accompanied by a paramagnetic to non-magnetic transition32,33,34,46, similar to the behavior in the family of Mo3O8 quantum magnets47. Two mildly different low-temperature structures with C2/m32 and R333,34 point group symmetry have been experimentally observed. The corresponding DFT band structures are shown in Fig. 8. The main difference between the C2/m and R3 structures is a deformation within the trimers, yielding slightly elongated trimers in the C2/m structure, and modifications to the trimer sizes between the different layers in the R3 structure, as depicted in Fig. 7. As a result, the degeneracies between the two higher-lying trimer states are lifted in both LT structures.
The main difference between these LT and HT bulk structures is, however, the relative shift between the layers. In the LT structures, trimers from different layers are partially significantly closer to each other than in the HT structure, c.f. Fig. 7. This enhances the inter-layer hybridization, which leads to a splitting of the two metallic bands around the Fermi level, which yields a full but small gap between these states. Also, the opposite signs of intra-trimer and inter-trimer in-plane hoppings (in the AO model) are peculiar for the electron localization at the trimer. While the competition between kinetic energy and intersite Coulomb interactions leads to a weak interaction limit for the HT structure with strong electron localization, LT phases, due to relatively larger inter-layer hopping but still much smaller than the on-site U, reveal some tendency to the strong interaction limit with inter-layer antiferromagnetic order. On the DFT level, it is important to note that none of the symmetry breakings in the C2/m and R3 structures yield significant charge re-distributions between the Nb atoms of the trimers.
The molecular orbital description is furthermore still valid and allows to quantify of the nearest-neighbor intra- and inter-layer hoppings yielding t∥ ≈ 15meV, \({t}_{1}^{\perp }\approx 127\) meV, \({t}_{2}^{\perp }\approx 3\) meV, respectively for the R3 structure. Notably, \({t}_{2}^{\perp }\) is much smaller than \({t}_{1}^{\perp }\), which is in turn much larger than t∥. The LT structures are thus best described as weakly hybridized stacks of bilayer Nb3Cl8, whereby the two layers forming the bilayers are strongly hybridized. The Coulomb interaction matrix elements are only barely affected by the relative shift between the two layers of the LT bulk unit cell yielding U ≈ 1.5 eV in the R3 structures, respectively. A similar description holds for the C2/m structure, however, with reduced symmetry. All model parameters are given in Table 3. This might suggest that the low-temperature bulk structure is best described as strongly antiferromagnetically coupled bilayers, which significantly suppresses the magnetic susceptibility in comparison to the weakly coupled high-temperature bulk phase. This would qualitatively explain experimentally measured magnetic susceptibilities32,33 without assuming vanishing magnetic moments.
We have also applied the Hubbard-I approximation to the bulk structures. As shown in ref. 48, the Hubbard-I approach corresponds to the formal first-order-in hopping correction to Green’s function, assuming that the interaction is local, which leads to vanishing vertex corrections. This assumption is still clearly valid in the case of the LT structures as the interactions between the trimers, as well as the hopping between them, is much smaller than the intertrimer Coulomb interaction. The only other factor, which could yield vertex corrections is correlated hopping1,2,49. Explicit calculations show here, however, that these contributions to the hopping are small: The largest Uiiij element with i and j being located on different trimers, which could be responsible for correlated hopping terms, is on the order of just 3 meV and can thus be safely neglected. In Fig. 8, we, therefore, present the corresponding interacting spectral functions for both atomic and MO models. Similar to the situations studied above, we find Mott gaps on the order of 1.6 eV driven by the dynamical properties of the Hubbard-I self-energy. Due to the small splitting of the two bands around the Fermi level, we see a similarly small splitting in the lower and upper Hubbard bands as well.
For the experimental verification of the Mottness, we compare in Fig. 9 the upper Hubbard-bands of all models (in the MO basis) to Hartree-Fock calculations, which are similar to LSDA+U approximations6. As also discussed in detail for elemental rare-earth and their compounds39,50, Hartree-Fock calculations cannot account for the significant bandwidth renormalizations, which are captured by Hubbard-I calculations and which have possibly been observed experimentally in Nb3Cl827,29. The LT bulk structures further show a particular behaviour of the split lower Hubbard band: just at A, these two bands touch while they are separated by about 100meV throughout the whole BZ. This is different in the Hartree-Fock calculations and could thus serve as an experimental hint towards the Mottness.
The color maps and red dashed lines represent the interacting spectral functions and electronic structures obtained using the Hubbard-I and Hartree-Fock approximation, respectively for (a) ML and (b–d) different bulk structures. The results are shown for the MO model (the electronic structures for the AO model are similar). The AFM interlayer order was used in the Hartree-Fock calculations for bulk structures.
The sister compound Nb3Br8 has been suggested to be an obstructed atomic insulator26 already at the DFT level, based on symmetry analysis with a small gap between flat bands51. Our results for Nb3Cl8 suggest that correlation effects could also be important in Nb3Br8 and that these would give a substantial contribution to any experimentally observed gap. To quantify this, cRPA calculations for Nb3Br8 are needed, especially to understand the interplay between Coulomb interactions and interalayer hybridization28 in the LT phases. In case Nb3Br8 is similarly correlated as Nb3Cl8, it could be the reason for the observed superconducting diode effect in heterostructures based on Nb3Br852.
In conclusion, based on detailed ab initio down folding calculations, we derived various minimal (generalized) Hubbard models for Nb3Cl8 in several structures. For all of them, the derived model parameters, together with the Hubbard-I approximation, suggest that Nb3Cl8 is a Mott insulator, independent of the details of the low- or high-temperature bulk or monolayer structures. For the monolayer structures, we were able to derive the most simple single-band Hubbard model. For bulk structures in all known lattice structures, we derived two-orbital Hubbard models with long-range Coulomb interactions.
Non-local Coulomb interactions are substantial in this layered compound. For the description of charge-neutral excitations in the monolayer, it is possible to use an effective Hubbard model with a modified local Hubbard interaction to account for this24. We need to stress that the role of non-local Coulomb interactions in the bulk structure should be investigated in more detail since the effective Hubbard model approach assumes that the non-local Coulomb interaction is the same in all directions, which is not the case in this layered compound.
Electronic correlations in the triangular lattice, as found in Nb3Cl8, are of particular theoretical interest because the geometric frustration in the lattice removes the antiferromagnetic fluctuations, which are so dominant in square lattice models53. Instead, there are indications for a quantum spin liquid phase at intermediate interaction strengths54,55,56. The analysis of electronic correlations in this work (using Hubbard-I) is restricted to strong interactions and to the undoped case, with one electron per trimer. Doping away from this integer filling will destroy the Mott insulating phase even at large U/t (see, e.g, Nb3Cl7Te57) and thus requires a more advanced many-body treatment of the arising correlation phenomena, such as possible chiral superconductivity58,59. Recent progress in advanced computational methods makes it possible to obtain converged multi-method results37 for the triangular lattice Hubbard model. Combining these methods with the model parameters derived here makes it possible to study the iconic Hubbard model and its physics hand-in-hand between theory and experiment.
Methods
Electronic structure calculations
We study the electronic and magnetic properties of Nb3Cl8 ML and bulk using one high-temperature structure (with space group \(P\bar{3}m1\)) and two low-temperature structures (characterised by R3 and C2/m space groups)32,33. The details about the primitive representation of the low-temperature structures and corresponding Wyckoff positions used in this work can be found in Supplementary Note 5.
We utilize two different Wannier basis sets representing the lowest trimer molecular orbital alone and an atomistic one describing the three relevant Nb d orbitals on the trimer-corner positions, which we refer to as the molecular orbital (MO) and atomic orbital (AO) models, respectively. To this end, we start with conventional DFT calculations utilizing the Perdew-Burke-Ernzerhof GGA exchange-correlation functional60 within a PAW basis61,62 as implemented in the Vienna Ab initio Simulation Package (vasp)63,64 using the structures given above. We use (20 × 20 × 1) and (8 × 8 × 4) k-meshes for monolayer and bulk calculations, respectively, as well as an energy cutoff of 350 eV and Methfessel-Paxton smearing of σ = 0.05 eV.
For the MO model, we project the flat Kohn-Sham bands around the Fermi level to an (initial) Wannier orbital with s symmetry located at the center of the trimer. For the atomistic model, we similarly project all Kohn-Sham states between −1.0 eV and +1.5 eV to three individual Nb-centered d orbitals. Afterward, we maximally localize the orbitals using the wannier90 package65 and applying an inner (frozen) window including either only the flat bands around EF or all states between −1.0 eV and +1.5 eV. Using the resulting localized orbitals ψi(r), we obtain the single-particle Wannier Hamiltonian from the hopping matrix elements
The resulting Wannier models perfectly interpolate all Kohn-Sham states in their respective windows, as indicated in Fig. 2 and Fig. 8.
The Coulomb interaction matrix elements Uijkl are evaluated within the Wannier orbital basis sets from above and using the constrained random phase approximation (cRPA) scheme31 according to
which utilizes the partially screened Coulomb interaction
Here \(\hat{v}\) is the bare Coulomb interaction and \({\widehat{\Pi }}_{{{\text{cRPA}}}}\) is the partial polarization as defined
with Πtarget describing all polarization contributions from within the target sub-space as defined by the Wannier functions. This way, we avoid any double counting of screening channels in subsequent solutions of the derived generalized Hubbard models. ΠcRPA correspondingly describes screening from all other states except the target ones, including from a significant amount of empty states from the full Kohn-Sham basis. In detail, we use in total 160 bands and define ΠcRPA using Kaltak’s projector method as recently implemented in vasp66.
From this, we derive the full retarded and non-local rank-4 Coulomb tensor Uijkl(ω) for both models. Casula et al. showed that using U(ω = 0) instead of the fully retarded U(ω) is justified when renormalized hopping parameters are utilized67. The corresponding renormalization factor was shown to scale with the characteristic cRPA plasmon frequency ωp. To this end, we show in Fig. 4U(ω) of the MO orbital model in the HT ML structure. This indicates that ωp ≈ 25 eV is large such that we can safely neglect retardation effects here and use only Uijkl(ω = 0).
All monolayer calculations are performed within a supercell of 25 Å height. All tabulated and mentioned Coulomb matrix elements refer to these calculations.
To extrapolate to the effectively free-standing monolayer and to take dielectric screening from the environment into account, we use our Wannier Function Continuum Electrostatics (WFCE) approach43 as applied in ref. 68. To this end, we start with the non-local bare Coulomb interaction of the monolayer as obtained from our cRPA calculations in momentum space. Within a matrix representation vαβ(q) using a product basis α, β = {n, m} we can diagonalize the Coulomb tensor
with vν(q) and \(\left\vert {v}_{\nu }(q)\right\rangle\) being the corresponding eigenvalues and eigenvectors of the Coulomb tensors and q = ∣q∣. Assuming that the eigenbasis does not drastically change upon the effects of the cRPA screening, we can thus represent the full cRPA Coulomb tensor as
where εν(q) are the corresponding pseudo-eigenvalues of the dielectric tensor describing the different screening channels. The leading eigenvalue v1(q) renders Coulomb penalties for mono-pole-like perturbations (all orbitally resolved electronic densities are in phase). The mono-pole-like screening as rendered by ε1(q) can be modeled by solving the Poisson equation for a dielectric slab of height h embedded in some different dielectric environment yielding
with
For \({\varepsilon }_{\,{{\text{sub}}}}^{{{\text{above}}}}={\varepsilon }_{{{\text{sub}}}}^{{{\text{below}}}\,}=1\), this describes the leading dielectric function of a free-standing monolayer, which we can fit to the cRPA data. With these fitting parameters, we can now modify the full cRPA Coulomb tensor to describe environmental screening rendered by finite \({\varepsilon }_{\,{{\text{sub}}}}^{{{\text{above}}}\,}\) and \({\varepsilon }_{\,{{\text{sub}}}}^{{{\text{below}}}\,}\). Due to the monopole-like character of this environmental screening, we only affect density-density Coulomb matrix elements in the very same way.
Trimer model
A single trimer can be described in tight-binding theory using the Hamiltonian \(\hat{H}={t}_{0}\left(\begin{array}{rcl}0&1&1\\ 1&0&1\\ 1&1&0\end{array}\right)\), which has eigenvalues E0 = 2t0, E± = − t0 (note that t0 is negative, so E0 < E±) and corresponding eigenvectors
with \(\lambda =\exp (2\pi i/3)\). For the Nb3Cl8 trimer, t0 = −0.325 eV, so the trimer gap 3∣t0∣ ≈ 1 eV.
In the lattice of trimers, we have to take into account the hopping between trimers (i.e., along the blue bonds in Fig. 1). In the molecular orbital model, the hopping between trimers is found to be t1 ≈ 22 meV. In the atomic orbital model, the hopping from the corner of one trimer to the nearest atom on the neighbouring trimer has an amplitude of 84 meV. Based only on this, one might have expected t1 ≈ 84/3 = 28 meV, but sub-leading matrix elements (with alternating signs) are responsible for corrections. For a triangular lattice with nearest-neighbour hopping, the bandwidth is 9t1 ≈ 200 meV.
For the Coulomb interaction, there are two effects that play a role when going from the atomic orbitals to the molecular orbitals. First, there is a purely geometric effect since the molecular orbitals are linear combinations of the atomic orbitals, which leads to a transformation of the Coulomb tensor. Secondly, additional screening processes take place when integrating out the two higher-lying molecular orbitals ψ±, which changes the concept of partially screened. Here, we consider the first effect since it can be understood simply. In this calculation of the Coulomb interaction, it is essential to realize that changes in the single-particle energies (chemical potential) occur simultaneously with the transformation of the Coulomb matrix. Therefore, the best way to relate matrix elements of two different Hamiltonians is to evaluate energy differences between sets of states with constant total particle number. In this case, we look at the energy of the trimer for n↑, n↓ = 0, 1. We use the fact that the electron density is homogeneously distributed over the three atoms for the low-lying molecular orbital, so n↑ = 1 corresponds to a density of 1/3 electron with spin ↑ per atom.
Here, U is the local Coulomb interaction in the atomic model, V is the nearest-neighbour Coulomb interaction in the atomic model, and \({U}^{{\prime} }\) is the Hubbard interaction in the molecular model. Now, we want E(n↑ = 1, n↓ = 1) + E(n↑ = 0, n↓ = 0) − E(n↑ = 1, n↓ = 0) − E(n↑ = 0, n↓ = 1) to be the same in both models, which requires \({U}^{{\prime} }=\frac{1}{3}U+\frac{2}{3}V\). This geometric estimate gives \({U}^{{\prime} }\approx 2.1\) eV, while the full cRPA gives \({U}^{{\prime} }\approx 1.9\) eV, which means that the additional screening is responsible for roughly 0.2 eV only. Note that more than half of the molecular Hubbard interaction comes from the interatomic Coulomb interaction V. This shows that a strictly Nb local Hubbard interaction is not a good approximation for the three-orbital atomic model, the interatomic interactions are just as important, similar to many two-dimensional hexagonal compounds24.
For the inter-trimer interactions, we find slightly smaller values for the molecular model compared to the atomic model, which can also be understood from the fact that the molecular model contains additional screening processes. For longer ranges, these screening processes are less efficient, and the difference between the interactions in the two models is smaller.
Hubbard-I
A simple and lightweight way to take into account correlation effects on top of density functional theory calculations is provided by the Hubbard-I approximation38. For our compound, we first calculate the self-energy of a single, isolated trimer using all intratrimer Coulomb matrix elements. Then, we insert this local self-energy into the lattice Green’s functions G = G0/(1 − ΣG0), where G0 is the Green’s function corresponding to the DFT band structure. The resulting spectral functions \(-\Im \{{{{\rm{Tr}}}}G(k,\omega )\}\) (or \(-\Im \{{\phi }_{0}^{\star }G(k,\omega ){\phi }_{0}\}\) its projection onto state ϕ0) are shown throughout the manuscript. We use TRIQS69 and the Hubbard-I solver implemented by Schüler et al.70 to perform the calculations. All calculations were performed using the inverse temperature β = 300eV−1 and the broadening of Green’s function on real frequencies δ = 0.05eV.
There is always a certain amount of freedom in choosing the chemical potential when connecting band structures and many-electron calculations. For an insulator such as Nb3Cl8, this simply leads to an overall energy shift for all states/bands, which does not affect the physics as long as the chemical potential lies within the gap. To facilitate the comparison, we have lined out the spectra in different panels of several figures based on the center of the lowest band.
Data availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Information. Additional data is available from the authors on reasonable request.
References
Schubin, S. & Wonsowsky, S. On the electron theory of metals. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 145, 159–180 (1934).
Vonsovsky, S. V. & Katsnelson, M. I. Some types of instabilities in the electron energy spectrum of the polar model of the crystal. I. The maximum-polarity state. Journal of Physics C: Solid State Physics 12, 2043–2053 (1979).
Vonsovsky, S. V. & Katsnelson, M. I. Some types of instabilities in the electron energy spectrum of the polar model of the crystal. II. The criterion of stability of a metallic state. Journal of Physics C: Solid State Physics 12, 2055–2064 (1979).
Gutzwiller, M. C. Effect of correlation on the ferromagnetism of transition metals. Phys. Rev. Lett. 10, 159–162 (1963).
Kanamori, J. Electron Correlation and Ferromagnetism of Transition Metals. Progress of Theoretical Physics 30, 275–289 (1963).
Hubbard, J. Electron correlations in narrow energy bands. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 276, 238–257 (1963).
Hubbard, J. Electron correlations in narrow energy bands. II. The degenerate band case. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 277, 237–259 (1964).
Hubbard, J. Electron correlations in narrow energy bands. III. An improved solution. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 281, 401–419 (1964).
Qin, M., Schäfer, T., Andergassen, S., Corboz, P. & Gull, E. The Hubbard model: A computational perspective. Annual Review of Condensed Matter Physics 13, 275–302 (2022).
Lieb, E. H. & Wu, F. Y. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension. Phys. Rev. Lett. 20, 1445–1448 (1968).
Metzner, W. & Vollhardt, D. Correlated lattice fermions in d = ∞ Dimensions. Phys. Rev. Lett. 62, 324–327 (1989).
Georges, A. & Kotliar, G. Hubbard model in infinite dimensions. Phys. Rev. B 45, 6479–6483 (1992).
LeBlanc, J. P. F. et al. Solutions of the two-dimensional Hubbard model: Benchmarks and results from a wide range of numerical algorithms. Phys. Rev. X 5, 041041 (2015).
Arovas, D. P., Berg, E., Kivelson, S. A. & Raghu, S. The hubbard model. Annual Review of Condensed Matter Physics 13, 239–274 (2022).
Andersen, O. K., Liechtenstein, A. I., Jepsen, O. & Paulsen, F. LDA energy bands, low-energy hamiltonians, \({t}^{{\prime} }\), t″, t⊥(k), and J⊥. J. Phys. Chem. Solids 56, 1573–1591 (1995).
Pavarini, E., Dasgupta, I., Saha-Dasgupta, T., Jepsen, O. & Andersen, O. K. Band-structure trend in hole-doped cuprates and correlation with \({T}_{c}^{\max }\). Phys. Rev. Lett. 87, 047003 (2001).
Lechermann, F. Late transition metal oxides with infinite-layer structure: Nickelates versus cuprates. Phys. Rev. B 101, 081110 (2020).
Kitatani, M. et al. Nickelate superconductors–a renaissance of the one-band hubbard model. npj Quantum Materials 5, 59 (2020).
Wilhelm, A., Lechermann, F., Hafermann, H., Katsnelson, M. I. & Lichtenstein, A. I. From Hubbard bands to spin-polaron excitations in the doped Mott material NaxCoO2. Phys. Rev. B 91, 155114 (2015).
Perfetti, L. et al. Spectroscopic Signatures of a Bandwidth-Controlled Mott Transition at the Surface of 1T − TaSe2. Phys. Rev. Lett. 90, 166401 (2003).
Hansmann, P., Ayral, T., Vaugier, L., Werner, P. & Biermann, S. Long-Range Coulomb Interactions in Surface Systems: A First-Principles Description within Self-Consistently Combined GW and Dynamical Mean-Field Theory. Phys. Rev. Lett. 110, 166401 (2013).
Hansmann, P., Vaugier, L., Jiang, H. & Biermann, S. What about U on surfaces? Extended Hubbard models for adatom systems from first principles. Journal of Physics: Condensed Matter 25, 094005 (2013).
Esslinger, T. Fermi-hubbard physics with atoms in an optical lattice. Annual Review of Condensed Matter Physics 1, 129–152 (2010).
Schüler, M., Rösner, M., Wehling, T. O., Lichtenstein, A. I. & Katsnelson, M. I. Optimal hubbard models for materials with nonlocal coulomb interactions: Graphene, silicene, and benzene. Phys. Rev. Lett. 111, 036601 (2013).
Wang, Y., Wu, H., McCandless, G. T., Chan, J. Y. & Ali, M. N. Quantum states and intertwining phases in kagome materials. Nature Reviews Physics 5, 635–658 (2023).
Xu, Y. et al. Three-dimensional real space invariants, obstructed atomic insulators and a new principle for active catalytic sites. Preprint at https://arxiv.org/abs/2111.02433 (2021).
Gao, S. et al. Discovery of a single-band mott insulator in a van der waals flat-band compound. Phys. Rev. X 13, 041049 (2023).
Zhang, Y., Gu, Y., Weng, H., Jiang, K. & Hu, J. Mottness in two-dimensional van der waals Nb3X8 monolayers (x = Cl, Br, and I). Phys. Rev. B 107, 035126 (2023).
Sun, Z. et al. Observation of topological flat bands in the kagome semiconductor Nb3cl8. Nano Letters 22, 4596–4602 (2022).
Yoon, J. et al. Anomalous thickness-dependent electrical conductivity in van der waals layered transition metal halide, nb3cl8. Journal of Physics: Condensed Matter 32, 304004 (2020).
Aryasetiawan, F. et al. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 70, 195104 (2004).
Sheckelton, J. P. Rearrangement of van der waals stacking and formation of a singlet state at t = 90 k in a cluster magnet. Inorg. Chem. Front. 4, 481–490 (2017).
Haraguchi, Y. et al. Magnetic-Nonmagnetic Phase Transition with Interlayer Charge Disproportionation of Nb3 Trimers in the Cluster Compound Nb3Cl8. Inorganic Chemistry 56, 3483–3488 (2017).
Kim, J. et al. Terahertz Spectroscopy and DFT Analysis of Phonon Dynamics of the Layered Van der Waals Semiconductor Nb3X8 (X = Cl, I). ACS Omega 8, 14190–14196 (2023).
van Loon, E. G. C. P., Rösner, M., Katsnelson, M. I. & Wehling, T. O. Random phase approximation for gapped systems: Role of vertex corrections and applicability of the constrained random phase approximation. Phys. Rev. B 104, 045134 (2021).
Casula, M., Rubtsov, A. & Biermann, S. Dynamical screening effects in correlated materials: Plasmon satellites and spectral weight transfers from a green’s function ansatz to extended dynamical mean field theory. Phys. Rev. B 85, 035115 (2012).
Wietek, A. et al. Mott insulating states with competing orders in the triangular lattice hubbard model. Phys. Rev. X 11, 041013 (2021).
Lichtenstein, A. I. & Katsnelson, M. I. Ab initio calculations of quasiparticle band structure in correlated systems: LDA++ approach. Phys. Rev. B 57, 6884–6895 (1998).
Locht, I. L. M. et al. Standard model of the rare earths analyzed from the Hubbard I approximation. Phys. Rev. B 94, 085137 (2016).
van Loon, E. G. C. P., Schüler, M., Katsnelson, M. I. & Wehling, T. O. Capturing nonlocal interaction effects in the hubbard model: Optimal mappings and limits of applicability. Phys. Rev. B 94, 165141 (2016).
Tang, H.-K. et al. The role of electron-electron interactions in two-dimensional dirac fermions. Science 361, 570–574 (2018).
Veld, Y., Schüler, M., Wehling, T. O., Katsnelson, M. I. & van Loon, E. G. C. P. Bandwidth renormalization due to the intersite coulomb interaction. Journal of Physics: Condensed Matter 31, 465603 (2019).
Rösner, M., Şaşıoğlu, E., Friedrich, C., Blügel, S. & Wehling, T. O. Wannier function approach to realistic coulomb interactions in layered materials and heterostructures. Phys. Rev. B 92, 085102 (2015).
van Loon, E. G. C. P. et al. Coulomb engineering of two-dimensional mott materials. npj 2D Materials and Applications 7, 47 (2023).
Koseki, S., Matsunaga, N., Asada, T., Schmidt, M. W. & Gordon, M. S. Spin-orbit coupling constants in atoms and ions of transition elements: Comparison of effective core potentials, model core potentials, and all-electron methods. The Journal of Physical Chemistry A 123, 2325–2339 (2019).
Pasco, C. M., El Baggari, I., Bianco, E., Kourkoutis, L. F. & McQueen, T. M. Tunable magnetic transition to a singlet ground state in a 2d van der waals layered trimerized kagomé magnet. ACS Nano 13, 9457–9463 (2019).
Nikolaev, S., Solovyev, I. & Streltsov, S. Quantum spin liquid and cluster Mott insulator phases in the Mo3O8 magnets. npj Quantum Mater 6, 25 (2021).
Lebègue, S. et al. Electronic structure and spectroscopic properties of thulium monochalcogenides. Phys. Rev. B 72, 245102 (2005).
Westerhout, T. & Katsnelson, M. I. Role of correlated hopping in the many-body physics of flat-band systems: Nagaoka ferromagnetism. Phys. Rev. B 106, L041104 (2022).
Peters, L. et al. Treatment of 4f states of the rare earths: The case study of TbN. Phys. Rev. B 89, 205109 (2014).
Regmi, S. et al. Observation of flat and weakly dispersing bands in the van der waals semiconductor Nb3Br8 with breathing kagome lattice. Phys. Rev. B 108, L121404 (2023).
Wu, H. et al. The field-free Josephson diode in a van der Waals heterostructure. Nature 604, 653–656 (2022).
Xu, M. et al. Frustration- and doping-induced magnetism in a fermi–hubbard simulator. Nature 620, 971–976 (2023).
Morita, H., Watanabe, S. & Imada, M. Nonmagnetic insulating states near the mott transitions on lattices with geometrical frustration and implications for κ-(et)2Cu2(CN)3. Journal of the Physical Society of Japan 71, 2109–2112 (2002).
Szasz, A., Motruk, J., Zaletel, M. P. & Moore, J. E. Chiral spin liquid phase of the triangular lattice hubbard model: A density matrix renormalization group study. Phys. Rev. X 10, 021042 (2020).
Chen, B.-B. et al. Quantum spin liquid with emergent chiral order in the triangular-lattice hubbard model. Phys. Rev. B 106, 094420 (2022).
Zhang, H. et al. Topological flat bands in 2D breathing-kagome lattice Nb3TeCl7. Advanced Materials 35, 2301790 (2023).
Zampronio, V. & Macrì, T. Chiral superconductivity in the doped triangular-lattice Fermi-Hubbard model in two dimensions. Quantum 7, 1061 (2023).
Huang, Y., Gong, S.-S. & Sheng, D. N. Quantum phase diagram and spontaneously emergent topological chiral superconductivity in doped triangular-lattice mott insulators. Phys. Rev. Lett. 130, 136003 (2023).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mat. Sci. 6, 15 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Mostofi, A. A. et al. wannier90: A tool for obtaining maximally-localised Wannier functions. Comp. Phys. Commun. 178, 685 – 699 (2008).
Kaltak, M. Merging GW with DMFT. PhD Thesis, University of Vienna (2015).
Casula, M. et al. Low-energy models for correlated materials: Bandwidth renormalization from coulombic screening. Phys. Rev. Lett. 109, 126408 (2012).
Soriano, D., Rudenko, A. N., Katsnelson, M. I. & Rösner, M. Environmental screening and ligand-field effects to magnetism in CrI3 monolayer. npj Computational Materials 7, 1–10 (2021).
Parcollet, O. et al. Triqs: A toolbox for research on interacting quantum systems. Computer Physics Communications 196, 398 – 415 (2015).
Schüler, M. Triqs/hubbardI - A Hubbard-I solver based on triqs atom_diag. available at: https://github.com/TRIQS/hubbardI (2022).
Acknowledgements
We thank Mazhar Ali for drawing our attention to distorted kagome materials and for fruitful discussions and feedback on the manuscript. E.v.L. acknowledges support from Gyllenstiernska Krapperupsstiftelsen, Crafoord Foundation, and the Swedish Research Council (Vetenskapsrådet, VR) under grant 2022-03090. M.R. and M.I.K. acknowledge support from the Dutch Research Council (NWO) via the “TOPCORE” consortium and from the research program “Materials for the Quantum Age” (QuMat) for financial support. The latter program (registration number 024.005.006) is part of the Gravitation program financed by the Dutch Ministry of Education, Culture and Science (OCW). The work of M.I.K. was further supported by the European Union’s Horizon 2020 research and innovation program under European Research Council Synergy Grant 854843 “FASTCORR”. Simulations were performed with computing resources granted by Dutch National Supercomputer Snellius under project EINF-4184.
Author information
Authors and Affiliations
Contributions
S.G. and M.R. performed all ab initio calculations. E.v.L. analysed the trimer model. S.G., E.v.L., and M.R. performed the Hubbard-I calculations. M.R. designed the study with assistance from E.v.L. All authors contributed to the data analysis and the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grytsiuk, S., Katsnelson, M.I., Loon, E.G.v. et al. Nb3Cl8: a prototypical layered Mott-Hubbard insulator. npj Quantum Mater. 9, 8 (2024). https://doi.org/10.1038/s41535-024-00619-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-024-00619-5