Orbital degree of freedom induced multiple sets of second-order topological states in two-dimensional breathing Kagome crystals

Abstract

The lattice geometry induced second-order topological corner states in breathing Kagome lattice have attracted enormous research interests, while the realistic breathing Kagome materials identified as second-order topological insulators are still lacking. Here, we report by first-principles calculations the second-order topological states emerging in two-dimensional d-orbital breathing Kagome crystals, i.e., monolayer niobium/tantalum chalcogenide halides M₃QX₇ (M = Nb, Ta; Q = S, Se, Te; X = Cl, Br, I). We find that the orbital degree of freedom of d orbitals can give rise to multiple sets of corner states. Combining fraction corner anomaly, orbital components and real space distribution of the corner states, we can also identify the topology of these corner states. Our work not only extends the lattice geometry induced second-order topological states to realistic materials, but also builds a clear and complete picture on their multiple sets of second-order topological states.

Introduction

The interplay between lattice geometry and topology at the quantum level can give rise to rich physical properties^{1,2,3,4,5,6,7,8,9,10}. A prototypical example is the two-dimensional (2D) Kagome lattice that is composed of corner-sharing triangles. Owing to the unusual lattice geometry, electron wavefunctions in Kagome lattice can be phase destructive to form topological flat bands by interference and can experience a nontrivial Berry phase to form Dirac cones at each valley, as shown in Fig. 1a. Such topological bands have been observed by angle-resolved photoemission spectroscopy in several Kagome materials, including Fe₃Sn₂^1,2, FeSn³, CoSn^4,5 and YMn₆Sn₆⁶. When turning the pair of corner-sharing triangles to different sizes (i.e. forming a breathing Kagome lattice), the Dirac cones will be gapped to produce an insulating state, as shown in Fig. 1b. Intriguingly, Ezawa found that the lattice geometry of breathing Kagome lattice can give rise to topological states located at the corner of the nontrivial triangular nanodisk, which is the hallmark of 2D higher-order topological insulators (TIs)¹¹.

Fig. 1: Bulk topology of ML Nb₃TeCl₇.

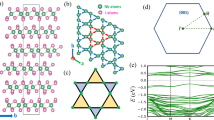
a, b TB bulk band structures of the conventional Kagome lattice and breathing Kagome lattice, respectively. c Atomic structure of ML Nb₃TeCl₇. The Nb atoms, Te atoms and Cl atoms are represented by gray, yellow and red spheres, respectively. d The unit cell of ML Nb₃TeCl₇ is indicated by the black rhombus. The Nb atoms form a breathing Kagome lattice indicated by gray bonds. The small triangle (triangle A) and big triangle (triangle B) are indicated by red and blue colors, respectively. e Calculated bulk band structure of ML Nb₃TeCl₇. The Fermi energy is shifted to zero Energy. f Calculated $\left[ {p_1\left( {k_2} \right),p_2\left( {k_1} \right)} \right]$ for Gap #1. Inset: schematic illustration of the position of the Wannier center $\left( {p_1,p_2} \right) = \left( {\frac{1}{3},\frac{2}{3}} \right)$. g Calculated $\left[ {p_1\left( {k_2} \right),p_2\left( {k_1} \right)} \right]$ for Gap #5. Inset: schematic illustration of the position of the Wannier center $\left( {p_1,p_2} \right) = \left( {\frac{2}{3},\frac{1}{3}} \right)$.

The exploration of higher-order TIs is at the forefront of condensed matter physics^{11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30}. Unlike the d-dimensional TIs that host (d − 1) dimensional topological boundary states^31,32,33, the higher-order TIs manifest robust boundary states with higher codimension^{11,12,13,14,15,16,17}. Specially, the 2D higher-order TIs that have gapless modes at the (d−2) dimensional boundary (corner states), but whose (d − 1) dimensional boundary states (edge states) are gapped are also called 2D second-order topological insulators (SOTIs). The 2D SOTIs can realize Majorana zero mode by constructing a SOTI/superconductor heterostructure where neither special pairing nor magnetic field is required^34,35. The lattice geometry induced second-order topological states in breathing Kagome lattice also attracted enormous research interests. So far, a series of artificial breathing Kagome materials have been constructed to realize the second-order topological states, such as acoustic systems^36,37, photonic crystals^38,39 and the artificially engineered molecular islands on Cu(111) surface⁴⁰. However, the realistic breathing Kagome materials identified as SOTIs are still lacking.

There are two main reasons that limit the research of second-order topology in realistic breathing Kagome materials. The first one is the challenge to find an ideal breathing Kagome material. The ideal breathing Kagome material is expected to have a stable 2D form (the breathing Kagome materials intensively studied recently (NH₄)₂[C₇H₁₄N][V₇O₆F₁₈]⁴¹ and Li₂In_1-xSc_xMo₃O₈⁴² do not conform to this condition due to their strong inter-plane interactions). Meanwhile, the low-energy bands should be dominated by the breathing Kagome atoms for the convenience of detecting the properties that originate from the breathing Kagome atoms. The second one is the difficulty of building a complete picture on the second-order topology of realistic breathing Kagome material (breathing Kagome lattice + orbital + non-Kagome atoms). The orbital degree of freedom in realistic breathing Kagome materials will complicate the situation greatly. Besides, the effect of the non-Kagome atoms is ambiguous. Moreover, since realistic breathing Kagome materials do not necessarily support (generalized) chiral symmetry, their corner states may hide in the bulk or edge bands. How to demonstrate the existence of the hidden corner states is still an open question.

Here, we find a series of ideal 2D d-orbital breathing Kagome crystals, i.e., monolayer (ML) M₃QX₇ (M = Nb, Ta; Q = S, Se, Te; X = Cl, Br, I). The three-dimensional crystals of these materials have been synthesized before^43,44,45,46 and can be feasibly cleaved to ML (2D form) by the mechanical exfoliation technique since their inter-layer coupling is van der Waals force. Meanwhile, the low energy bands are dominated by the breathing Kagome atoms (M atoms). In this work, we take ML Nb₃TeCl₇ as a representative example to study its second-order topology from the bulk, edge and corner aspects, respectively. ML Nb₃TeCl₇ features six d-orbital global bulk gaps consecutive in energy due to the inversion symmetry breaking. We find three of the six gaps possess nonzero bulk polarization, where two of them own Wannier center at the small triangle center and the third one at hexagon center, indicating there will be two sets of nontrivial corner states and one set of trivial corner states for triangle nanodisk stacked by big triangles (Configuration 1). The calculation of edge spectrums shows that the pairs of gapped edge bands only emerge on the edge of Configuration 1. Meanwhile, these edge bands are symmetric about the ~0.88 eV energy level, indicating the existence of approximate (generalized) chiral symmetry in this system, which will collect the corner states near by the ~0.88 eV. To show the second-order topology directly, we calculate the energy spectrum of the triangular nanodisk of Configuration 1. We find two sets of corner states emerge in the energy gap around 0.88 eV. The corner state sets are nondegenerate due to the crystal field effect imposed by the non-Kagome atoms. The corner states in a single set are nondegenerate due to the finite-size effect. To demonstrate the existence of the third set of corner states and establish the correspondence between the number of bulk gap with nonzero polarization and the set number of corner states, we count the state number in corner spectrum and find the third set of corner states concealed in the upper bulk and edge bands.

Results

Lattice structure and bulk band structure

As shown in Fig. 1c, the 2D d-orbital breathing Kagome crystal Nb₃TeCl₇ possess a layered structure where the breathing Kagome atoms (Nb atoms) are sandwiched between chalcogen (Te atoms) or halogen atoms (Cl atoms), while each Nb atom is encompassed by one Te atom and five Cl atoms to form NbTeCl₅ octahedron. As shown in Fig. 1d, the breathing Kagome lattice is composed of corner-sharing triangles A and B, which are of different sizes, i.e., triangle A (the small triangle) and triangle B (the big triangle). By calculating the bulk band structure [Fig. 1e] and projected density of states (PDOS) [Supplementary Fig. 1], we find that the fifteen low-energy bands in energy region −1.5 eV ~ 3.8 eV are dominated by Nb 4d orbitals, indicating the d-orbital character of the breathing Kagome lattice. From Fig. 1e, we can see that there are six d-orbital global bulk gaps, as indicated by Gap #1 ~ #6. Form the symmetry aspect, we point out that such global bulk gaps are induced by the inversion symmetry breaking [see detailed discussion in Supplementary Note II]. Noting the d-orbital character of the breathing Kagome crystal, to study its second-order topology, all the d-orbital global bulk gaps should be taken into consideration. To identify the topology of the six global bulk gaps, we will calculate the bulk polarization (Wannier center) of them below.

Bulk polarization (Wannier center)

The bulk polarization (Wannier center) can be calculated by the Wilson-loop method^47,48,49,50. The gauge-invariant Wilson loop is defined as a path ordered product of the exponential of Berry connections^51,52. The b₁-directed (b₁ and b₂ are the reciprocal lattice vectors) Wilson loop is a path ordered product of F_i computed along the b₁ direction from (k₁, k₂) to (k₁ + 1, k₂) following the form:

$$W\left( {k_2} \right) = W_{\left( {k_1 + 1,k_2} \right) \leftarrow \left( {k_1,k_2} \right)} = \mathop {{\lim }}\limits_{N \to \infty } F_{N - 1}F_{N - 2} \cdots F_1F_0.$$

(1)

The matrix element of $F_i$ is obtained by $\left[ {F_i} \right]_{mn} = \left\langle {u_m\left( {\frac{{i + 1}}{N},k_2} \right){{{\mathrm{|}}}}u_n\left( {\frac{i}{N},k_2} \right)} \right\rangle$, where $u_m$ and $u_n$ are the occupied Bloch wavefunctions. The k₁ and k₂ direction are parallel to the b₁ and b₂ respectively, respectively. Define a Hamiltonian $H_W\left( {k_2} \right)$ via

$$W\left( {k_2} \right) \equiv {{{\mathrm{e}}}}^{{{{\mathrm{i}}}}2{\uppi}H_W\left( {k_2} \right)}$$

(2)

and calculate the eigenvalues of $H_W\left( {k_2} \right)$, referred to as $\left\{ {\nu _i\left( {k_2} \right)} \right\}$. Then the eigenvalues of $H_W\left( {k_2} \right)$ over the occupied bands are

$$p_1\left( {k_2} \right) = \mathop {\sum}\limits_{i = 1}^{N_{occ}} {v_i} \left( {k_2} \right).$$

(3)

The associated Wannier center is

$$p_1 = \frac{1}{N}\mathop {\sum}\limits_{k_2} {p_1} \left( {k_2} \right).$$

(4)

Similarly, the Wannier center $p_2$ can be obtained from b₂-directed Wilson loop. The $p_1\left( {p_2} \right)$ shows the fractional coordinate of the Wannier center along lattice vector ${{{\boldsymbol{a}}}}_1\left( {{{{\boldsymbol{a}}}}_2} \right)$. The Wannier centers $\left( {p_1,p_2} \right)$ for Gap #1 ~ #6 are calculated as $\left( {\frac{1}{3},\frac{2}{3}} \right)$, $\left( {0,0} \right)$, $\left( {\frac{1}{3},\frac{2}{3}} \right)$, $\left( {0,0} \right)$, $\left( {\frac{2}{3},\frac{1}{3}} \right)$ and $\left( {0,0} \right)$, respectively. The $\left[ {p_1\left( {k_2} \right),p_2\left( {k_1} \right)} \right]$ for Gap #1 and Gap #5 and the corresponding Wannier center schematically drawn in the insets are shown in Fig. 1f, g. The Wannier center $\left( {p_1,p_2} \right) = \left( {\frac{1}{3},\frac{2}{3}} \right)$ resides at the small triangle center [the inset of Fig. 1f], while the Wannier center $\left( {p_1,p_2} \right) = \left( {\frac{2}{3},\frac{1}{3}} \right)$ resides at the hexagon center [the inset of Fig. 1g], which does not exist in s-orbital breathing Kagome lattice. In s-orbital breathing Kagome lattice, the Wannier center is located at one kind of triangle center³⁶.

For the Configuration 1, the Wannier center at small triangle center corresponds to Wyckoff position c, while the Wannier center at the hexagon center corresponds to Wyckoff position b, as shown in Fig. 2b, c. The Wannier center at Wyckoff position c gives rise to 1/3 fractional edge charge, but 0 fractional corner charge. The Wannier center at Wyckoff position b gives rise to 2/3 fractional edge charge and 1/3 fractional corner charge. According to the definition of fractional corner anomaly (FCA)⁵³:

$$\phi = \rho - \left( {\sigma _1 + \sigma _2} \right){{{\mathrm{mod}}}}\,1,$$

(5)

where $\sigma _1$ and $\sigma _2$ are the edge-localized fractional mode density and $\rho$ is the corner-localized fractional mode density, we obtain that the FCA of Wannier center at Wyckoff position c equals to 1/3 (nontrivial), while the FCA of Wannier center at Wyckoff position b equals to 0 (trivial). Therefore, for Configuration 1, the two bulk gaps with Wannier center at small triangle center will give rise to two sets of nontrivial corner states, while the bulk gap with Wannier center at hexagon center will give rise to one set of trivial corner states. Such trivial corner states are explained by the decoration of topological edges⁵⁴.

Fig. 2: Wyckoff position of ML Nb₃TeCl₇.

a The black hexagons represent unit cell with C₃ symmetry. The English letters a, b and c inside the unit cell indicate the maximal Wyckoff positions. b, c The Wannier center at position c and b for Configuration 1, which is stacked by big triangles. d The Wannier center at position a for Configuration 2, which is stacked by small triangles.

We also calculate the bulk polarization with the original point at small triangle center and find the bulk polarization of all the gaps is zero. Therefore, for Configuration 2, as shown in Fig. 2d, the Wannier center of all the gaps is located at Wyckoff position a and such Wyckoff position will give rise to neither fractional edge charge nor fractional corner charge.

Edge spectrum

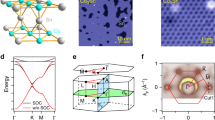
To see the edge topology clearly, we consider these two typical edges. As schematically shown in Fig. 3a, the edge of Configuration 1 is named as type-I edge, while the edge of Configuration 2 is named as type-II edge. We then calculate the edge spectrum of these two edges. As shown in Fig. 3b, in energy region 0–1.6 eV, type-I edge hosts two pairs of gapped edge bands (massive Dirac fermion), i.e., edge band 1_up (2_up) and 1_down (2_down), which are absent for type-II edge [Fig. 3c]. The pairing of the edge bands is found out by comparing their orbital components [Fig. 3d], since the paired edge bands have the same orbital components. Meanwhile, the band structures projected to the Nb 1^st, 2^nd and 3^rd layer [the Nb 1^st, 2^nd and 3^rd layer is indicated in Fig. 3a] show that these paired edge bands are mainly contributed by outmost-layer Nb atoms of type-I edge [Fig. 3d–f]. Due to the alternative bond lengths of outmost-layer Nb atoms, the paired edge bands can be described by one-dimensional (1D) Su-Schrieffer-Heeger (SSH) models. Since 1D SSH model describing a real material always has a Z₂ topological invariant, mirror-related type-I edges belong to different Z₂ classifications. Therefore, the intersection of two mirror-related type-I edges corresponds to a domain wall for the edge theory, which harbors a localized corner state^55,56,57. The edge bands are symmetric about the ~0.88 eV energy level [Fig. 3b, d], indicating the approximate (generalized) chiral symmetry in this system. Then the corner states will be collected near by the ~0.88 eV. In addition, the edge bands indicated by the white arrows in Fig. 3b, c are identified to be first-order helical edge states under the introduction of spin-orbit coupling (SOC) and have no connection with the second-order topology [Supplementary Note V].

Fig. 3: Edge topology of ML Nb₃TeCl₇.

a Schematic drawing of type-I and type-II edge. Type-I edge is the edge of Configuration 1, while type-II edge is the edge of Configuration 2. The Nb 1^st, 2^nd and 3^rd layer of type-I edge is indicated by numbers. b, c The type-I and type-II edge spectrums, respectively. The two pairs of edge bands for type-I edge are indicated by “1_up”, “1_down” and “2_up”, “2_down”. The edge bands that turn to first-order helical edge states under SOC are indicated by white arrows. d–f Band structures projected to the Nb 1st layer, 2nd layer and 3rd layer, respectively. The contribution of five 4d orbitals is indicated by different colors.

Corner spectrum

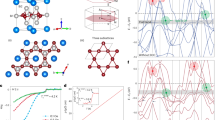
To identify the second-order topology of ML Nb₃TeCl₇ directly, we calculate the energy spectrum of a triangle nanodisk of Configuration 1, as shown in Fig. 4a. The three type-I edges are associated by the mirror symmetry, as shown in Fig. 4b, c. The size of the nanodisk is $L = 8$. The $L$ is the number of the Nb triangle on each nanodisk edge. Remarkably, one observes two sets of states with three states in each set in the ~0.88 eV energy gap. As clearly shown in Fig. 4b, c, each set of states are well localized at the three corners, indicating they are two sets of corner states. The two sets of corner states are referred to as CS-I and CS-II, respectively [Fig. 4a–c]. We note that CS-I and CS-II are not degenerate where CS-II is located at higher energy level than CS-I [Fig. 4a]. To understand the main mechanism, we focus on the environment of Nb 4d orbitals, i.e., the effect of the non-Kagome atoms. Since each Nb atom is encompassed by one Te atom and five Cl atoms to form NbTeCl₅ octahedron, the Nb 4d orbitals will be split to two high-energy e_g orbitals (dz², dx²y²) and three low-energy t_2g orbitals (dxy, dyz, dxz) by the crystal field effect [Fig. 3d]. Noting that the NbTeCl₅ octahedron is inclined, to obtain the correct e_g and t_2g orbital components, the previous d orbitals should be rotated by using the equation:

$$Y_{l,m}\left( {{{\boldsymbol{r}}}} \right) = \mathop {\sum}\limits_{m{^\prime} = - l}^l {D_{m,m{^\prime}}^{\left( l \right)}} \left( {R\left( {\alpha ,\beta ,\gamma } \right)} \right)^ \ast Y_{l,m{^\prime}}\left( {{{{\boldsymbol{r}}}}^\prime } \right),$$

(6)

where ${{{\boldsymbol{r}}}} = R{{{\boldsymbol{r}}}}^\prime$ and $D_{m{^\prime},m}^{\left( l \right)}\left( {\alpha ,\beta ,\gamma } \right) = e^{ - im{^\prime}\alpha }d_{m{^\prime},m}^{\left( l \right)}\left( \beta \right)e^{ - im\gamma }$. $Y_{l,m}\left( {{{\boldsymbol{r}}}} \right)$ is the spherical harmonics; $D_{m{^\prime},m}^{\left( l \right)}\left( {\alpha ,\beta ,\gamma } \right)$ is the Wigner-D functions; $d_{m{\prime},m}^{\left( l \right)}\left( \beta \right)$ is the Wigner-d functions and $\beta$ is the angle between rotated (Nb-Te direction) and previous (out of plane direction) z-direction [indicated in Fig. 4(d)]. Here, $l = 2$ and $\alpha = - \frac{\pi }{4}$, $\beta = 0.213\pi$, $\gamma = \frac{\pi }{4}$. The rotated orbital components are shown in Table 1. We find that the CS-II (36.7% e_g, 63.3% t_2g) owns more e_g orbital components and less t_2g orbital components than CS-I (28.6% e_g, 71.4% t_2g). Thereby the crystal field effect makes CS-II located at higher energy position than CS-I.

Fig. 4: Corner states of ML Nb₃TeCl₇.

a Energy spectrum of the triangular nanodisk of Configuration 1 ($L = 8$) of ML Nb₃TeCl₇. Energy levels are plotted in ascending order. Two sets of corner states are indicated by blue solid circles. The inset: enlarged drawing of CS-I and CS-II. The three corner states of CS-I are labeled as $\varphi _1$, $\varphi _2$ and $\varphi _3$, respectively. b, c The calculated local density of states of CS-I and CS-II, respectively. The three equivalent mirrors M_x are indicated by red dashed lines. d Schematic drawing of crystal field splitting of Nb 4d orbitals in NbTeCl₅ octahedron. The inset shows the NbTeCl₅ octahedron. The angle between rotated (Nb-Te direction) and previous (out of plane direction) z-direction is $\beta$. e The solid (dotted) line shows the energy splitting ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}}$ (absolute value of ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}}$) as a function of nanodisk size $L$. The inset shows the effective model to interpret the finite-size effect. The inter-corner effective hopping is $t$.

Table 1 The previous (P) and rotated (R) orbital components of CS-I and CS-II.

We also note that the corner states in a single set are also not degenerate. CS-I splits into one nondegenerate state $\varphi _1$ and two degenerate states $\varphi _2$ and $\varphi _3$ [termed as (1+2)], as shown in the inset of Fig. 4a. To show the origin of the splitting, the energy splitting ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}}$ of CS-I (defined as the energy level of the nondegenerate state minus the degenerate states) depending on the nanodisk size $L$ is calculated, as shown in Fig. 4e. The absolute value of ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}}$ decays exponentially with increasing $L$, indicating that the splitting originates from the finite-size effect. The finite-size effect can be interpreted by an effective model where three isolated corner states interact with each other, as schematically shown in the inset of Fig. 4e. The Hamiltonian $H_p$ of this effective model takes the form:

$$H_p = - \left( {\begin{array}{*{20}{c}} 0 & t & t \\ t & 0 & t \\ t & t & 0 \end{array}} \right),$$

(7)

where $t$ is the inter-corner effective hopping. The eigenvalues of $H_p$ are $E_1 = - 2t$ and $E_{2,3} = t$ and corresponding eigenvectors can be $\varphi _{1p} = \frac{1}{{\sqrt 3 }}\left( {\begin{array}{*{20}{c}} 1 \\ 1 \\ 1 \end{array}} \right)$, $\varphi _{2p} = \frac{1}{{\sqrt 6 }}\left( {\begin{array}{*{20}{c}} 2 \\ { - 1} \\ { - 1} \end{array}} \right)$ and $\varphi _{3p} = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ { - 1} \end{array}} \right)$, respectively. In the model results, corner states split into (1 + 2). Meanwhile, the local density distribution of $\varphi _{1p}$, $\varphi _{2p}$ and $\varphi _{3p}$ is consistent with our first-principles calculations [Supplementary Fig. 4]. Hence the finite-size effect is well interpreted by the effective model. Through the model, we know that ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}} = - 3t$. Then the oscillation of ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}}$ [Fig. 4e] originates from the sign change of the effective hopping $t$. The result that ${\Delta}{{{\mathrm{E}}}}_{{{{\mathrm{split}}}}}$ of CS-II is smaller than CS-I [inset of Fig. 4a] can also be explained. It is because that the more localized CS-II [Fig. 4b, c] ought to host smaller effective hopping $t$ than CS-I.

The three bulk gaps with nonzero polarization indicate that there are three sets of corner states. The third one is not observed in the energy gap around 0.88 eV [Fig. 4a]. To demonstrate the existence of the third set of corner states and establish the correspondence between the number of bulk gap with nonzero polarization and the set number of corner states, we propose a method to determine which bulk or edge bands the third set of corner states hide in. As shown in Fig. 5a, for the phase with zero bulk polarization, there are $\left( {L + 1} \right)L/2$ states in each bulk band. Therefore, as shown in Fig. 5b, for Nb₃TeCl₇ nanodisk of Configuration 2 $\left( {L = 8} \right)$, there are 36 states between green arrows (one bulk band), 72 states between purple arrows (two bulk bands). As shown in Fig. 5c, for the phase with nonzero bulk polarization, there are $(L - 1)(L - 2)/2$ states in each bulk band, $3(L - 1)$ states in each edge band and 3 states in each set of corner states. Therefore, as shown in Fig. 5d, for Nb₃TeCl₇ nanodisk of Configuration 1 $\left( {L = 8} \right)$, there are 21 states between the yellow arrows (one edge band), 42 states between the green arrows (one bulk band and one edge band). Noting that the edge states that turn to first-order helical edge states under SOC are attributed to the bulk bands, it is supposed to be 84 states between the purple arrows (two bulk bands and two edge bands). However, there are 87 (84 + 3) states between the purple arrows, indicating there is a set of corner states hidden between the purple arrows. Therefore, the third set of corner states is found concealed in the upper bulk and edge bands. This method can also be examined by the situation in Ta₃SBr₇ and Nb₃SI₇ [Supplementary Fig. 7]. For Ta₃SBr₇ where three sets of corner states emerge in the energy gap, the calculated state number between the purple arrows is 84; for Nb₃SI₇ where only one set of corner states emerges in the energy gap, the calculated state number between the purple arrows is 90 (84 + 3 × 2).

Fig. 5: Demonstrating the existence of the hidden corner states of ML Nb₃TeCl₇.

a Schematic showing the state number of a $L$-size nanodisk with zero bulk polarization. b Counting the state number of the Nb₃TeCl₇ nanodisk of Configuration 2 $\left( {L = 8} \right)$. There are 36 states between green arrows and 72 states between purple arrows. c Schematic showing the state number of a $L$-size nanodisk with nonzero bulk polarization. d Counting the state number of theNb₃TeCl₇ nanodisk of Configuration 1 $\left( {L = 8} \right)$. There are 21 states between yellow arrows, 42 states between green arrows and 87 states between purple arrows.

Since the trivial corner states originate as decoration of the edge states, they should have similar orbital components as the edge states and be less localized than the topological corner states. Here, CS-I has the approximately the same orbital components as edge band 1_up and 1_down and be less localized than CS-II. Through the orbital components and real space distribution, we can identify CS-I as the trivial corner states. One can also observe that the two sets of topological corner states (CS-II and CS-III) have similar real space distribution [Supplementary Fig. 10-2]. In these breathing Kagome crystals, the topological corner states are protected by the C₃ and mirror symmetry. The effect of mirror symmetry is to pin the corner states to the corners. Breaking mirror symmetry, the corner states will move to generic points on the side. As long as the C₃ symmetry is present, the corner states are stable yet not pinned to corners in the absence of mirror symmetries. To annihilate the corner states, the only way is large C₃ symmetry breaking either in the bulk or on the boundary.

Discussion

To summarize, we find a series of ideal 2D d-orbital breathing Kagome crystals, i.e., M₃QX₇ (M = Nb, Ta; Q = S, Se, Te; X = Cl, Br, I) and identify their second-order topology from the bulk (Wannier center), edge (pairs of gapped edge bands), and corner (localized corner states) aspects by first-principles calculations. Our work not only extends the lattice geometry induced second-order topological states to realistic materials, but also builds a clear and complete physical picture on the multiple sets of topological corner states in realistic breathing Kagome materials with d-orbital character. The d orbital degree of freedom gives rise to three sets of corner states in these systems. These corner state sets are collected nearby the same energy level by approximate (generalized) chiral symmetry. Meanwhile, the corner state sets consisting of different d-orbital components are nondegenerate due to the crystal field effect imposed by the non-Kagome atoms. The corner states in a single set split to [1 + 2] due to the finite-size effect. To demonstrate the existence of the hidden corner states and establish the correspondence between the number of bulk gap with nonzero polarization and the set number of corner states, we propose a method to determine the bulk or edge bands that these corner states hide in. Combining FCA, orbital components and real space distribution of the corner states, we also identify the topology of these corner states. Moreover, the coexistence of corner states (this work) and topological flat bands¹⁰ in 2D d-orbital breathing Kagome crystals make them potential candidates to investigate the correlation between second-order topology, first-order Z₂ topology and possible superconductivity, which awaits future validation.

Finally, we want to discuss the experimental implementation of the topological corner states in these breathing Kagome crystals. The feasible detection of the corner states is essentially important, since the experimental signature that unambiguously identifies such states in realistic materials is still lacking. These breathing Kagome crystals are stable and readily available^43,44,45,46. Meanwhile, the predicted energy gap reaches 0.350 eV in Ta₃SBr₇ [Supplementary Fig. 7a], which is much larger than 0.1 eV in graphdiyne²², facilitating the experimental detection of corner states by utilizing local measurement techniques. A significant application of the corner states is to realize Majorana zero mode³⁴. Although the three sets of corner states are not located at Fermi level, they can be selectively modulated to the Fermi level by appropriate local potentials⁵³.

Methods

Calculation method

The first-principles calculations based on density functional theory are performed with Vienna ab initio simulation package^58,59. The projector-augmented wave pseudopotential⁶⁰ and Perdew–Burke–Ernzerhof exchange-correlation functional⁶¹ are used. The energy cutoff of plane-wave basis is set as 350 eV and the vacuum space is set to be larger than 15 Å. The first Brillouin zone is sampled according to the Γ-centered scheme. We use a k mesh of 6 $\times$ 6 $\times$ 1 for structural optimization and 12 $\times$ 12 $\times$ 1 for the self-consistent calculations. The positions of the atoms are optimized until the convergence of the force on each atom is less than 0.01 eV/Å. The convergence condition of electronic self-consistent loop is $10^{ - 5}$ eV. In order to study the topological properties of ML M₃QX₇ (M = Nb, Ta; Q = S, Se, Te; X = Cl, Br, I), we firstly construct the Hamiltonian in Wannier basis by using Wannier90 package^62,63,64. The dz², dxz, dyz, dx²-y² and dxy orbitals of each M atom are chosen as projection orbitals. Moreover, the corresponding edge spectrum are obtained from the Hamiltonian by using iterative Green’s function method^65,66,67.