Abstract
Magnetic skyrmions are vortex-like spin textures, which are usually treated as two-dimensional objects. In their lattice state, they form well-ordered, hexagonal structures, which have been studied in great detail. To obtain a three-dimensional (3D) skyrmion crystal, these planes can be envisaged to be stacked up forming skyrmion strings in the third dimension. Here, we report the observation of a 3D skyrmion phase in Cu2OSeO3 by carrying out reciprocal space mapping in resonant elastic x-ray scattering. We observe regions in the magnetic field-cooling phase diagram in which the skyrmion phase apparently coexists with the conical phase. However, such a coexistence is forbidden due to symmetry arguments. Instead, the skyrmion strings themselves are periodically modulated along their axes, as confirmed by micromagnetic simulations. The periodic modulation is in fact a necessary consequence of the evolution of the skyrmion phase out of the conical state and should therefore be a universal property of skyrmion strings in chiral helimagnets.
Similar content being viewed by others
Introduction
Magnetic skyrmions are two-dimensional (2D) vortex-like spin textures, which are ordered in the form of hexagonally packed lattices and which are found in all helimagnetic B20 materials, such as MnSi, FeCoSi, FeGe, and Cu2OSeO31,2,3. These 2D lattices have been explored extensively4 and the understanding of the interaction between skyrmions and with their surroundings5,6, as well as external driving forces7,8,9,10,11,12, led to a plethora of device proposals13,14,15,16,17.
Initially, the skyrmion lattice was treated as a rigid system, forming homogeneous strings in the third dimension1,2. Starting with the discovery of magnetic monopoles at branching points of the skyrmion strings18, it became evident that, as in all ordered structures, defects are playing a major role for the lattice properties. Furthermore, recent experiments have shown that the skyrmion lattice is not rigid, but susceptible to field and temperature variations19.
Nevertheless, the number of experimental studies aimed at exploring the 3D magnetic structure of skyrmion crystals is rather limited. Most of them are transmission techniques, such as electron microscopy2,20,21, x-ray scanning transmission microscopy22,23, x-ray holography, and small angle x-ray scattering19,24, which are limited to the study of thin membranes. Others, such as magnetic force microscopy, make use of the depth dependence of the magnetic contrast18. Further, new developments in magnetic imaging have emerged, such as hard x-ray vector nanotomography25, which assemble 3D images of an object through reconstruction from a series of 2D measurements.
Another approach utilizes resonant elastic x-ray scattering (REXS) in the soft x-ray range to obtain access to magnetically ordered states tied to magnetic 3D elements26,27,28. By varying the energy of the incident x-rays across the absorption edge, information from different depths is obtained. This allows for a reconstruction of the 3D magnetic structure below the surface, i.e., essentially performing tomographic mapping of near-surface structures29. In combination with the polarization dependence of the scattering, all three components of the magnetization vector can be accessed30,31,32, and further insight into the topological properties such as the helicity angle and winding number can be gained29,33,34.
So far, no experimental evidence for any periodic modulation of skyrmion strings has been found. Interestingly, it has been hypothesized that if skyrmion strings were to exhibit a conical modulation, their interparticle interactions would undergo a fundamental change and become attractive35. This is in contrast to the repulsive interactions understood to be associated with 2D skyrmions5,6. While their modulation has not been measured, attractive skyrmions have been reported for thin Cu2OSeO3 membranes36.
Here, we demonstrate the stabilization of a conically modulated skyrmion string lattice through REXS. Most commonly, skyrmion lattices are studied with the field applied perpendicular to the sample plane, and as the strings are oriented along the field direction, they form a hexagonally packed lattice in the sample plane. Here, we apply the field in-plane and with the skyrmion strings following the field direction, the strings will lie in the plane of the sample while keeping their hexagonal arrangement37. The conical modulation is superimposed on the axis of the skyrmion string, providing the experimental 3D view of a periodic skyrmion string modulation. We explore the transition between modulated and unmodulated strings, demonstrating the possibility of tuning the nature of skyrmion interactions.
Results
Resonant elastic x-ray scattering
For the study of the magnetic states of Cu2OSeO3 with the field in-plane, we employ the reflection geometry as illustrated in Fig. 1a. Soft x-ray REXS is suited for the study of compounds consisting of 3D magnetic elements. With the photon energy tuned to the L3 edge, the magnetic scattering cross-section is comparable to its charge scattering counterpart27. The applied in-plane field (along the x direction) forces the skyrmion strings to lie in the sample plane, keeping their hexagonal order lattice arrangement (see Fig. 1f)37. In reciprocal space, the six magnetic reciprocal lattice points of the skyrmion lattice phase lie in a plane (shaded in green) in the vicinity of the (001) peak (shown in red). This (0, qy, qz) plane is perpendicular to the sample plane.
a Illustration of the ω-2θ scattering geometry with ki and ks, the incident and scattered wave vectors, respectively. The REXS measurements were carried out with circularly polarized x-rays tuned to the Cu L3 absorption edge. The magnetic field B is applied along the x direction, i.e., in-plane, to allow for direct probing of the skyrmion strings, and z∥ [001] surface normal. The reciprocal space around the structural (001) reciprocal lattice point (red) is shown at diffraction condition, i.e., intersecting the Ewald sphere. The six magnetic satellites in the skyrmion phase (in green) lie in the (0, qy, qz) plane. b From 2θ and ω rocking scans, the scattered intensity in the (0, qy, qz) (out-of-plane cut) and (qx, qy,1) (in-plane cut) planes is reconstructed. The measured scattering contrast for c–e the modulated skyrmion phase is compared with the expected contrast for the (perfectly ordered) f–h pure skyrmion and i–k conical phases. In the first column, the magnetic structures are illustrated that lead to the scattering patterns in the (0, qy, qz) and (qx, qy,1) planes shown in the second and third column, respectively.
To determine the reciprocal magnetic lattice around the structural peak, reciprocal space mapping (RSM) is used4,27. In RSM, CCD images are collected for a sufficiently large combination of ki and ks, from which the reciprocal space volume, and in particular the qy–qz (out-of-plane) and qy–qx (in-plane) cuts (Fig. 1b), can be reconstructed. Note that while the Ewald sphere is curved, its radius is sufficiently large such that the flat CCD camera captures magnetic scattering images even if the diffraction conditions are not strictly met. As this mode of operation is much faster than doing a full RSM, the exploration of the magnetic phase diagram and the field dependence of the scattering vector were carried out in the faster CCD imaging mode.
Figure 1c–e shows scattering from a modulated skyrmion lattice, Fig. 1f–h from a pure skyrmion lattice, and Fig. 1i–k from the conical phase in the out-of-plane (blue column) and in-plane cuts (yellow column), respectively. In the skyrmion lattice phase (Fig. 1f–h), in which the skyrmion strings lie in-plane, oriented along the applied magnetic field direction, the six spots in the qy–qz plane (qx = 0) lie on a circle and are representative of the hexagonally ordered lattice. The experimental data in Fig. 1d clearly show four skyrmion peaks at finite qy values (obtained at 56 K and 15 mT), whereas the other two (at qy = 0) are masked by the structural peak which is broadened along the qz direction. This broadening effect is due to the finite penetration depth of the x-rays at resonance, essentially making it a surface diffraction experiment37,38. As such, the reciprocal space points degenerate into crystal truncation rods (along qz), through which the Ewald sphere cuts to give elongated elliptical features instead of sharply defined Bragg peaks. It is well established that magnetically ordered systems near the surface give rise to magnetic truncation rods, which can be studied with surface diffraction techniques37,39. A systematic REXS study of the depth dependence of surface probing of skyrmions in Cu2OSeO3 can be found in ref. 37. On the other hand, no scattering peaks are expected in the qy–qz plane for the conical phase (Fig. 1j).
In contrast, the in-plane cuts in the (qx, qy,1) plane present a different picture (yellow column in Fig. 1 on the right-hand side). In the pure skyrmion phase, two peaks should be observable for qz = 1 ± δ, i.e., cutting through one of the horizontal pairs at finite qy (where δ is the small qz offset). However, due to the limited probing depth, the spots will be broadened along qz and observable in the qz = 1 plane. In the conical phase, two peaks are expected as well (for a perfectly ordered system), however, now being oriented along the applied field direction (i.e., qy = 0). The experimental data in Fig. 1e show a coexistence of the magnetic scattering features of both the skyrmion and conical phase at the same time.
Magnetic phases in Cu2OSeO3
Figure 2a–c shows magnetic scattering patterns of the common phases in the (qx, qy,1) plane. The four scattering peaks in Fig. 2a indicate helical magnetic ordering, with a modulation vector ±qh, and the presence of two domains due to the magnetocrystalline anisotropy of Cu2OSeO3. At 10 mT, the helical peaks have already moved toward the applied field direction—a trend that continues with increasing field until the conical phase is reached, with two peaks aligned along qx (see Fig. 2c).
Experimental magnetic scattering images obtained in the (qx, qy,1) plane around the (001) structural Bragg peak using the field-cooling protocol (B∥qx). The scattering contrast in a–c is associated with helical/conical, skyrmion, and conical and skyrmion ordering, respectively (at 45 K). In d, all phases, as well as higher-order skyrmion peaks, are present at the same time (at 35 K). The dashed white lines in d indicate boundaries to the integration region of the respective phases used for further analysis in Fig. 3.
The (pure) skyrmion phase (at 25 mT) shows two characteristic peaks aligned along qy (Fig. 2b), resulting from the projection of the sixfold symmetric skyrmion pattern in the qy–qz plane (Fig. 1g) onto the (qx,qy,1) plane. At 30 mT, i.e., at the upper field boundary of the skyrmion phase, both conical peaks (aligned along qx) and skyrmion peaks (aligned along qy) are observed, now coexisting (Fig. 2c). Finally, a mixed helical/conical and skyrmion state is found, as shown in Fig. 2d (35 K, 20 mT), also giving rise to intensity in higher-order (HO) skyrmion peaks (at larger ±qy values).
These results show that helical and conical spin modulations can be stabilized with the field applied in-plane, and that the skyrmion lattice forms in the plane normal to the applied field direction, i.e., skyrmion strings stretch along the field direction in the sample plane37. Next, we explore the surprising finding of the independent, as well as concurrent presence of helical/conical spin modulations and the skyrmion lattice phase, by carrying detailed phase maps of the respective existence regions.
Magnetic phase diagrams
Magnetic field-temperature maps, as shown in Fig. 3, were obtained by plotting the scattered intensity from the skyrmion and helical/conical phases as a function of temperature and field. First, the scattering data were transformed into polar coordinates, followed by the integration of the scattered intensity in the regions of interest. The skyrmion regions of interest for the first-order and HO peaks are defined as sectors in polar coordinates, labeled “first” and “HO” in Fig. 2d, and those of the helical/conical phase as “hel/con.” The results for the helical/conical phase are shown in Fig. 3a, b in the left column. For the skyrmion phase, apart from the commonly observed first-order peaks (in the inner horizontal sectors in Fig. 2b), also HO peaks are observed (in the outer horizontal sectors in Fig. 2d). The corresponding phase diagrams are shown in Fig. 3c, d (middle column) and Fig. 3e, f (right column), respectively. Owing to the strong magnetic history dependence of the magnetic phase diagram of Cu2OSeO340, we investigated the response of the system using a field-cooling (FC) (top row, Fig. 3a, c, e) and a zero FC (ZFC) protocol (bottom row, Fig. 3b, d, f).
The magnetic field-temperature phase diagrams show the scattered peak intensity for the helical/conical phase in a and b. For the skyrmion phase, the maps for the (ordinary) first-order peaks are shown in c and d and those for the higher-order peaks in e and f. Both phase diagrams differ notably. The measurements were carried out using a, c, e a field-cooling and b, d, f zero-field-cooling protocol, as illustrated by white arrows in the insert (starting from the high-temperature, low-field point shown in yellow). The white dotted and dashed lines in the plots provide a guide to the eye for comparing the position of the two skyrmion pockets between the panels. Note that the higher-order skyrmion peaks become much more intense when the helical/conical and skyrmion reflections coexist, indicating a transformation of the magnetic structure. The circles show the data extracted from the example images in Fig. 2.
The phase diagrams show that the different magnetic phases generally have well-defined boundaries, with the helical/conical phase pocket shown in Fig. 3a, b and the skyrmion pockets in Fig. 3c–f. The transition temperature TC is 57 K, above which no magnetic scattering intensity is observed.
Following the FC protocol (Fig. 3c), the first-order skyrmion phase pocket extends to much lower temperatures in comparison to the ZFC data (Fig. 3d), which we ascribe to a surface metastable state37. A metastable state can also be achieved by quenching40 or electric fields41. For comparison, the boundaries of the ZFC skyrmion pocket (visible in Fig. 3d) are indicated by dotted white lines in all panels. From Fig. 3b, d, it is clear that the helical/conical phase does not coexist with ZFC skyrmions. Instead, when the ZFC protocol is used, variation of the external magnetic field induces a first-order phase transitions between the helical/conical states and the skyrmion phase.
On the other hand, when following the FC protocol (comparing Fig. 3a, c), the coexistence of the phases is observed. As an example, the phase point at 45 K and 30 mT is highlighted in Fig. 3a, c, showing both helical/conical and skyrmion scattering intensity. The position of this pocket coincides with the high-temperature side of the FC first-order skyrmion pocket (Fig. 3c), and indeed, a pure skyrmion phase is, e.g., observed at 45 K and 25 mT. However, beyond its boundaries, the helical/conical and skyrmion phases coexist over a wide range of fields and temperatures following the FC protocol.
In the coexistence region of the phase diagram, in which both helical/conical and skyrmion reflections are observed, second-order skyrmion peaks become visible. Their intensity distribution within the magnetic phase diagram following the FC protocol is shown in Fig. 3e (dashed white line). No intensity is observed following the ZFC protocol (Fig. 3f).
Field and temperature dependence of the magnetic propagation vector
The scattering patterns, as shown in Fig. 2, also allow for the detailed study of the propagation vector, q, of the respective magnetic order, which is important for gaining a deeper understanding the nature of the phase coexistence. Figure 4 shows the field dependence of q at 45 K (FC protocol), both in terms of the polar angle of the scattering vector, ϕ (Fig. 4a), and the magnitude q = ∣q∣ (Fig. 4b), as defined in Fig. 4c.
Field-dependent scattered intensity maps for a the angle ϕ and b the magnitude ∣q∣ of the scattering vector, as defined in c. The measurements shown in a and b were carried out at 45 K using the field-cooling protocol. The temperature dependence of the ϕ-field plots is shown for 30, 35, 40, 45, and 50 K, in d–h, respectively. The red and green color scale data in b correspond to the intensity from the helical/conical and skyrmion modulation, respectively. These intensity plots are obtained by integrating within the regions of interest for the conical/helical and first-order skyrmion peaks as shown in Fig. 2d.
The scattered intensity from the first-order skyrmion phase is found along qy in Fig. 2b, c, i.e., ϕ = 90°. Looking at Fig. 4a, it can be seen that ϕ remains close to 90° across the entire field range, above the onset field of 13 mT (at 45 K). The magnitude of q is shown for the skyrmion lattice phase (green color scale) in Fig. 4b. This region extends over the same field range with no significant change with field (average ∣q∣ ≈ 0.016 r.l.u. (reciprocal lattice units)).
On the other hand, the field-dependent features in Fig. 4a, which exist at low (and even zero) field, are associated with the helical phase. With increasing field (in the vertical direction, i.e., at ϕ = 0° and 180°), the spins become more aligned with the field and the peaks bend toward the field direction. For the 45 K data, the helical/conical peak intensity vanishes above 20 mT and reappears at 28 mT as the fully aligned conical peak (ϕ = 0° and 180°). The field dependence of q for the helical/conical modulation is shown in Fig. 4b (red color scale). Here, the helical modulation shows an increase in q with field, reaching a maximum of ~0.030 r.l.u. for both the helical and conical modulations. For the entire temperature range probed, we did not observe a coexistence of the helical and conical phase42.
In comparison, the skyrmion lattice orientation remains fixed right from the onset of the phase at 13 mT. On the other hand, at this field, the modulation vector of the helical/conical structure is governed by both anisotropy and applied field. It is only above 28 mT (at the lowest temperature of 30 K) that the field dominates the orientation of the chiral spin structure, exhibiting the conical phase.
The temperature dependence of the scattering vector, as shown in Fig. 4d–h, is most pronounced at higher temperatures, where the transition from helical-to-conical phase is broadened. At lower temperatures, on the other hand, the transition between the helical and conical phase is more abrupt, showing almost a step-like transition at 30 and 35 K. The transition between the states remains continuous, without a gap, up to 45 K. At 50 K, the temperature dependence of ϕ is even steeper than at 45 K, and the transition gap is wider. This general behavior is to be expected as the increase in thermal energy allows the helical state to adjust its orientation more readily to the applied field. At lower temperatures, this rotation is predominantly governed by the Zeeman energy and occurs at a critical field in an abrupt way.
Micromagnetic modeling
To investigate localized topological states that can coexist with the conical phase, a hysteresis loop was calculated numerically on a unit of topological charge; a video of the states obtained as a function of external field can be found in the Supplementary Information. The system was found to occupy the helical state for low external fields, before transitioning into the conically modulated skyrmion state at higher fields. As the external field increased further, the conical tilt angle approached 0°, until the conical state became field-polarized and the conically modulated skyrmion state smoothly transitioned into the unmodulated skyrmion state.
The numerically obtained sharp transition from helices to conically modulated skyrmions is best captured in Fig. 4d. This is no coincidence; the micromagnetic calculations were carried out at zero temperature, and as can be seen by comparing Fig. 4d–h, reductions in temperature correspond to a more rapid appearance of the conically modulated skyrmion state.
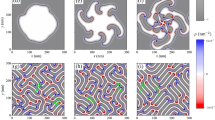
A typical image of the conically modulated skyrmion state obtained from this field dependence is given in Fig. 5, where the modulation along a single skyrmion string and of a modulated skyrmion lattice state is shown. Simulation details can be found in the “Methods” section.
a Visualization of a single skyrmion string embedded in the conical state (from left to right, mx-, my-, and mz-component of the magnetization). The core of the skyrmion is modulated periodically, with a period exactly matching that of the conical state. b Illustration of the conically modulated skyrmion lattice state.
Discussion
The conical state and the skyrmion lattice phase are known to exist in separate areas of the field-temperature phase diagram. Here, we have demonstrated that both phases are independent and that they can not only appear on their own but also in conjunction. There is no significant change in the helical/conical q when the system also hosts skyrmions, and the skyrmion q remains unaffected when the intensity from the helical phase disappears at 20 mT and then reappears as the conical phase at 28 mT (see Fig. 4). This means that the propagation vectors associated with the two modulations, which occur in perpendicular directions, are independent of one another. Further note that the conical phase is a bulk state and not a pinned surface state, as we found in a previous depth-dependent study of in-plane magnetic ordering in Cu2OSeO337.
Most notably, the conically modulated skyrmion state was only observed after FC the system. FC extends the skyrmion state toward lower temperatures as the nucleation of the skyrmion lattice happens within the boundaries of the standard skyrmion pocket, and when the temperature is lowered, there is insufficient energy to transition out of the skyrmion state. This metastable skyrmion state then coexists with the helical/conical phase. A similar process appears to be present for the conical/helical modulation. When passing through the skyrmion phase pocket, the system adopts a pure skyrmion state, and no helical/conical modulation is observed in the pocket highlighted by a dashed white line in Fig. 3. However, below a critical temperature, while the skyrmion phase is still present, the helical/conical modulation appears, i.e., there must be a lower energy barrier for the adoption of the helical/conical modulation than for the unwinding of the skyrmion phase.
As the skyrmion lattice nucleates within a conically modulated spin system, we hypothesized that the skyrmion strings become conically modulated in this magnetic environment. To confirm this hypothesis, we show that the conventional picture of an unmodulated skyrmion breaks down when surrounded by the conical state, and find numerically that this leads to conical modulation of the skyrmion strings.
As skyrmions exist on length scales typically more than an order of magnitude larger than the interatomic spacing, it is prudent to study them under the micromagnetic approximation. We assume that the discrete lattice of magnetic moments localized at atomic sites is well described by a continuous magnetization field \(\mathbf{m}\left(\mathbf{r}\right)\). In this formalism, the Hamiltonian for a material with a DMI constant D and exchange constant J in the presence of an external magnetic field B can be written as:
Typically, the skyrmion state is obtained by assuming that it takes the form of an arbitrary azimuthally symmetric vector field. If the stabilizing external magnetic field is taken to be parallel to the x-axis, such a vector field can be written as:
Here, the saturation magnetization is taken to be 1, \({C}_{\theta }=\cos \left(n\theta +\gamma \right)\) and \({S}_{\theta }=\sin \left(n\theta +\gamma \right)\), where γ is the helicity of the skyrmion and n is the topological winding number. Throughout this discussion, θ represents the azimuthal angle, and r the radial distance, in polar coordinates. Substituting Eq. (2) into a micromagnetic energy functional (such as Eq. (1)), the radial Euler–Lagrange equations can be solved numerically, or approximated analytically, to find the radial profile f(r) of an azimuthally symmetric skyrmion6.
Similarly, if the conical k-vector is parallel to the x-axis with a tilt angle ψ0, the conical state can be written as.
If skyrmions are embedded within the conical state, we require the asymptotic behavior.
While one could try imposing \({{{\mathrm{lim}}}\,}_{r\to \infty }f(r)={\psi }_{0}\), Eqs. (2) and (3) can then only be equated if k = n = 0. These conditions would impose that both states are trivially uniformly magnetized; for any cone state \({\mathbf{m}}_{{{{\rm{Con}}}}}\) with finite periodicity (k ≠ 0), and any topologically nontrivial skyrmion state (n ≠ 0), the unmodulated skyrmion state given in Eq. (2) is completely incompatible with the conical state given in Eq. (3). While, in principle, the scattering pattern shown in Fig. 2c could be due to phase-separated areas of unmodulated skyrmions and cones, our numerical analysis shows that when a skyrmion is contained within the conical state, it has to acquire a conical modulation, as visualized in Fig. 5.
The observation of second-order skyrmion peaks in the overlapping helical/conical and skyrmion phase regions (see Fig. 3e) provides further evidence for a direct modulation of the skyrmion strings. The structure factor of an ordinary, undistorted skyrmion lattice shows the highest intensity in the first-order peaks. HO peaks are typically observed in well-ordered skyrmion crystals43. One possibility is that the skyrmion crystal becomes more ordered, driven by the attractive skyrmion–skyrmion interaction. Or, this observation could simply indicate the existence of a richer in-plane structure that can only be described by HO Fourier modes. An example of such a conically modulated system, in the form of the modulated skyrmion lattice state, is shown in Fig. 5b.
In summary, we investigated the coexistence of helical/conical spin modulations with the skyrmion lattice state in Cu2OSeO3. This overlap occurs when FC through the skyrmion phase. The propagation vectors for the modulations in each phase appear independent, and show no effect on each other during the transitions in and out of the skyrmion or helical/conical phase. Using theoretical arguments, we found that the coexistence of these two phases, i.e., unmodulated skyrmions and conical modulations, is energetically not preferred. Instead, micromagnetic simulations show that the coexistence of the conical and skyrmion phase imposes a conical modulation on the skyrmion state. Our results provide further insight into the crossover regions between the magnetic phases in Cu2OSeO3, and, most importantly, indicate the occurrence of a conically modulated skyrmion string phase.
Methods
Resonant magnetic x-ray scattering
The soft x-ray REXS measurements were carried out on a high-quality Cu2OSeO3 single crystal (measuring 2 × 3 mm2) in the ultrahigh vacuum diffractometer RASOR44 on beamline I10 at the Diamond Light Source (Didcot, UK). The [001]-oriented sample was mounted on a liquid helium cooled sample holder, allowing for variable temperatures down to 10 K. A magnetic field was applied to the sample by two permanent magnets, whereby the field strength and direction within the scattering plane can be controlled by the separation and orientation of the two magnets, respectively. For this experiment, the field was applied along the in-plane [110] direction of Cu2OSeO3, i.e., along the x direction (see Fig. 1, \(y\parallel [\bar{1}10]\), z∥[001]). The incident x-rays are scattered by periodic features, and the scattered intensity is measured using an x-ray sensitive CCD camera. For x-rays with their photon energy tuned to the L3 edge of Cu (931.25 eV, λ = 13.3 Å), the (forbidden, see ref. 27) (001) peak is accessible in reflection due to the relatively large lattice constant of Cu2OSeO3 of 8.9193 Å (cubic P213 structure). At this energy, the scattered polarized x-rays are also sensitive to the periodic magnetic order within the crystal, and the magnetic diffraction spots resulting from incommensurate periodic order decorate the structural Bragg peak. Further, with the x-ray energy tuned precisely to the L3 absorption edge at 931.2 eV, the x-ray attenuation length at normal incidence is 95 nm in Cu2OSeO345, i.e., the probed volume is limited to a near-surface region. For the given scattering geometry, the REXS sampling depth, defined as the 1/e drop of the intensity, is 31 nm37,45.
In order to probe the magnetic states, RSM was carried out, allowing for the extraction of the magnetic modulation vectors. For magnetic RSM, ki and ks are systematically varied via ω sample rocking and scans of the 2θ detector arm. For each combination of parameters, a CCD image is recorded and the 3D reciprocal space volume can be reconstructed. Diffraction occurs for q = (001) ± qm, where qm is a magnetic modulation vector as illustrated in Fig. 1a, b. With ∣qm∣ ≪ ∣q∣, rocking the sample by typically ±2.5° around the (001) peak is sufficient to probe the entire relevant reciprocal space.
Numerical modeling
Within the micromagnetic approximation, a continuous magnetization field is assumed to describe the discretized local magnetic moments. The micromagnetic model Hamiltonian is given in Eq. (1), and stable magnetization configurations extremize this energy functional. As opposed to directly integrating these Euler–Lagrange equations, stable magnetization configurations were calculated by integrating the Landau–Lifshitz–Gilbert equation using the Fidimag package46, subject to the materials parameters: saturation magnetization MS = 3.84 × 105 A m−1, J = 8.78 × 10−12 J m−1, and D = 1.58 × 10−3 J m−2. The technique of finite differences was used with cell size dx = dy = dz = 2.5 nm, and geometry size Lx = Ly = 250 nm and Lz = 125 nm; the geometry was periodic in x and y, but finite in z. External fields ranging from 0 to 400 mT were applied, rotated from the z-axis by an angle of 3° to break symmetry. The results of the simulations are shown in Fig. 5.
Data availability
The data supporting the findings of this study are available from the corresponding authors on reasonable request.
References
Mühlbauer, S. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Adams, T. Long-wavelength helimagnetic order and skyrmion lattice phase in Cu2OSeO3. Phys. Rev. Lett. 108, 237204 (2012).
Zhang, S. L. Multidomain skyrmion lattice state in Cu2OSeO3. Nano Lett. 16, 3285–3291 (2016).
Lin, S. Z., Reichhardt, C., Batista, C. D. & Saxena, A. Particle model for skyrmions in metallic chiral magnets: dynamics, pinning, and creep. Phys. Rev. B 87, 214419 (2013).
Brearton, R., van der Laan, G. & Hesjedal, T. Magnetic skyrmion interactions in the micromagnetic framework. Phys. Rev. B 101, 134422 (2020).
Jonietz, F. Spin transfer torques in MnSi at ultralow current densities. Science 330, 1648–1651 (2010).
Yu, X. Z. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 3, 988 (2012).
Jiang, W. Blowing magnetic skyrmion bubbles. Science 349, 283–286 (2015).
Woo, S. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Zhang, S. L. Manipulation of skyrmion motion by magnetic field gradients. Nat. Commun. 9, 2115 (2018).
White, J. S. Electric-field-driven topological phase switching and skyrmion-lattice metastability in magnetoelectric Cu2OSeO3. Phys. Rev. Appl. 10, 014021 (2018).
Sampaio, J. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 8, 839–844 (2013).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Song, K. M. Skyrmion-based artificial synapses for neuromorphic computing. Nat. Electron. 3, 148–155 (2020).
Zhang, X. Skyrmion-electronics: writing, deleting, reading and processing magnetic skyrmions toward spintronic applications. J. Phys.: Condens. Matter 32, 143001 (2020).
Guang, Y. Electron beam lithography of magnetic skyrmions. Adv. Mater. 32, 2003003 (2020).
Milde, P. Unwinding of a skyrmion lattice by magnetic monopoles. Science 340, 1076–1080 (2013).
Burn, D. M. Field and temperature dependence of the skyrmion lattice phase in chiral magnet membranes. Phys. Rev. B 101, 14446 (2020).
Park, H. S. Observation of the magnetic flux and three-dimensional structure of skyrmion lattices by electron holography. Nat. Nanotechnol. 9, 337–342 (2014).
Zheng, F. Experimental observation of chiral magnetic bobbers in B20-type FeGe. Nat. Nanotechnol. 13, 451–455 (2018).
Birch, M. T. Real-space imaging of confined magnetic skyrmion tubes. Nat. Commun. 11, 1726 (2020).
Zeissler, K. Diameter-independent skyrmion hall angle observed in chiral magnetic multilayers. Nat. Commun. 11, 428 (2020).
Yamasaki, Y. Dynamical process of skyrmion-helical magnetic transformation of the chiral-lattice magnet FeGe probed by small-angle resonant soft x-ray scattering. Phys. Rev. B 92, 220421 (2015).
Donnelly, C. Three-dimensional magnetization structures revealed with x-ray vector nanotomography. Nature 547, 328–331 (2017).
Dürr, H. A. Chiral magnetic domain structures in ultrathin FeP”d films. Science 284, 2166–2168 (1999).
Zhang, S. L. Resonant elastic x-ray scattering from the skyrmion lattice in Cu2OSeO3. Phys. Rev. B 93, 214420 (2016).
Chauleau, J.-Y. Chirality in magnetic multilayers probed by the symmetry and the amplitude of dichroism in x-ray resonant magnetic scattering. Phys. Rev. Lett. 120, 037202 (2018).
Zhang, S. L. Reciprocal space tomography of 3D skyrmion lattice order in a chiral magnet. Proc. Natl. Acad. Sci. USA 115, 6386–6391 (2018).
van der Laan, G. Soft x-ray resonant magnetic scattering of magnetic nanostructures. Comptes Rendus Phys. 9, 570–584 (2008).
Zhang, S. L., van der Laan, G. & Hesjedal, T. Direct experimental determination of spiral spin structures via the dichroism extinction effect in resonant elastic soft x-ray scattering. Phys. Rev. B 96, 094401 (2017).
Zhang, S. L. Direct observation of twisted surface skyrmions in bulk crystals. Phys. Rev. Lett. 120, 227202 (2018).
Li, W. Anatomy of skyrmionic textures in magnetic multilayers. Adv. Mater. 31, 1807683 (2019).
Zhang, S. L., van der Laan, G. & Hesjedal, T. Direct experimental determination of the topological winding number of skyrmions in Cu2OSeO3. Nat. Commun. 8, 14619 (2017).
Leonov, A. O., Monchesky, T. L., Loudon, J. C. & Bogdanov, A. N. Three-dimensional chiral skyrmions with attractive interparticle interactions. J. Phys. Condens. Matter 28, 35LT01 (2016).
Loudon, J. C. Direct observation of attractive skyrmions and skyrmion clusters in the cubic helimagnet Cu2OSeO3. Phys. Rev. B 97, 134403 (2018).
Zhang, S. L. Robust perpendicular skyrmions and their surface confinement. Nano Lett. 20, 1428–1432 (2020).
Robinson, I. K. Crystal truncation rods and surface roughness. Phys. Rev. B 33, 3830–3836 (1986).
Fasolino, A., Carra, P. & Altarelli, M. X-ray resonant magnetic scattering from surfaces. Phys. Rev. B 47, 3877–3881 (1993).
Wilson, M. N. Stability and metastability of skyrmions in thin lamellae of Cu2OSeO3. Phys. Rev. Res. 2, 013096 (2020).
Okamura, Y., Kagawa, F., Seki, S. & Tokura, Y. Transition to and from the skyrmion lattice phase by electric fields in a magnetoelectric compound. Nat. Commun. 7, 12669 (2016).
Rybakov, F. N., Borisov, A. B., Blügel, S. & Kiselev, N. S. New spiral state and skyrmion lattice in 3D model of chiral magnets. New J. Phys. 18, 045002 (2016).
Adams, T. Long-range crystalline nature of the skyrmion lattice in MnSi. Phys. Rev. Lett. 107, 217206 (2011).
Beale, T. A. W. RASOR: an advanced instrument for soft x-ray reflectivity and diffraction. Rev. Sci. Instrum. 81, 073904 (2010).
van der Laan, G. & Figueroa, A. I. X-ray magnetic circular dichroism-a versatile tool to study magnetism. Coord. Chem. Rev. 277-278, 95–129 (2014).
Bisotti, M.-A. Fidimag–a finite difference atomistic and micromagnetic simulation package. J. Open Source Softw. 6, 22 (2018).
Acknowledgements
The REXS experiments were carried out in the RASOR diffractometer on beamline I10 at the Diamond Light Source, UK, under proposals SI17402 and MM21868. S.L.Z. acknowledges the starting grant from ShanghaiTech University and the Eastern Scholar Scheme. K.J.R. acknowledges the support from the Shanghai Sailing Program (Grant No. 20YF1430600). T.H. acknowledges financial support by the Engineering and Physical Sciences Research Council (UK) under grant number EP/N032128/1.
Author information
Authors and Affiliations
Contributions
D.M.B., S.L.Z., T.H. and G.v.d.L. designed and performed the experiments. D.M.B. carried out the data analysis. K.J.R. grew and prepared the samples. R.B. performed the numerical calculations. D.M.B., R.B. and T.H. wrote the manuscript with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Burn, D.M., Brearton, R., Ran, K.J. et al. Periodically modulated skyrmion strings in Cu2OSeO3. npj Quantum Mater. 6, 73 (2021). https://doi.org/10.1038/s41535-021-00373-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-021-00373-y
This article is cited by
-
Toggle-like current-induced Bloch point dynamics of 3D skyrmion strings in a room temperature nanowire
Nature Communications (2022)