Electron–hole superfluidity in strained Si/Ge type II heterojunctions

Abstract

Excitons are promising candidates for generating superfluidity and Bose–Einstein condensation (BEC) in solid-state devices, but an enabling material platform with in-built band structure advantages and scaling compatibility with industrial semiconductor technology is lacking. Here we predict that spatially indirect excitons in a lattice-matched strained Si/Ge bilayer embedded into a germanium-rich SiGe crystal would lead to observable mass-imbalanced electron–hole superfluidity and BEC. Holes would be confined in a compressively strained Ge quantum well and electrons in a lattice-matched tensile strained Si quantum well. We envision a device architecture that does not require an insulating barrier at the Si/Ge interface, since this interface offers a type II band alignment. Thus the electrons and holes can be kept very close but strictly separate, strengthening the electron–hole pairing attraction while preventing fast electron–hole recombination. The band alignment also allows a one-step procedure for making independent contacts to the electron and hole layers, overcoming a significant obstacle to device fabrication. We predict superfluidity at experimentally accessible temperatures of a few Kelvin and carrier densities up to ~6 × 10¹⁰ cm⁻², while the large imbalance of the electron and hole effective masses can lead to exotic superfluid phases.

Introduction

Spatially indirect excitons in a semiconductor system are a highly sought alternative for achieving quantum condensation and superfluidity in solid-state devices at experimentally accessible temperatures. Excitons are electrons and holes that bind into pairs through their long-range Coulombic attraction. Spatially indirect excitons have the electrons and holes confined in two separated but closely adjacent quantum wells or quasi two-dimensional (2D) layers^1,2. In the spatially indirect configuration, the electron–hole attraction can be very strong, while at the same time the electrons and holes are prevented from mutually annihilating through recombination.

From an application perspective, a supercurrent in the electron–hole superfluid could carry an electric current if the electron and hole layers are independently contacted in a counterflow configuration, directly leading to applications in dissipationless solid-state electronics^3,4. Furthermore, the superfluid can be continuously tuned from the strongly coupled Bose–Einstein condensation (BEC) bosonic regime to the BCS–BEC crossover regime of less strongly coupled fermionic pairs, simply by varying the carrier density using metal gates. In addition, when the electron and hole masses in a semiconductor are different, there are predictions of exotic superfluid phases⁵, including the Fulde–Ferrell–Larkin–Ovchinnikov phase⁶ and the Sarma phase with two Fermi surfaces⁷. These exotic phases are predicted to occur at much higher temperatures than in mass-imbalanced ultracold atomic gas Fermi mixtures^8,9.

2D van der Waals systems show particular promise because they offer the possibility of ultra-thin insulating barriers and conducting layers, with very strong electron–hole pairing interactions as a result. There have been predictions of quantum condensation of spatially indirect excitons in double bilayer graphene¹⁰ and double transition metal dichalcogenide (TMD) monolayers¹¹, and recent experiments have provided strong evidence for quantum condensation in these systems^12,13. One aspect of graphene bilayers and TMD monolayers is that the electron and hole effective masses are nearly equal, making these systems unsuitable for generating exotic superfluid phases. However, the most pressing limitation of the 2D van der Waals systems lies in the rudimentary methods employed for device fabrication. These entail a layer by layer assembly using pick and transfer techniques which are prone to layer wrinkling, contamination and misorientation¹⁴, leading to very poor device yield with limited prospects for scalability.

A more scalable approach is based on spatially indirect excitons in conventional semiconductor heterostructures, such as electrons and holes in GaAs double quantum wells (DQW). The system has been studied both with capacitively induced carriers^15,16 and optically excited carriers^17,18,19. However, despite promising indications of quantum condensation at very low temperatures, direct evidence for equilibrium superfluidity remains elusive in this rather mature material system. The intrinsic properties of the GaAs/AlGaAs band structure constitute the major constraints for excitonic condensation²⁰, particularly superfluidity, and they also pose severe challenges in device fabrication and operation²¹. GaAs heterostructures are grown by molecular beam epitaxy. This growth technique is not compatible with conventional complementary metal-oxide semiconductor technology, so that prospects for advanced manufacturing and large scale device integration are severely limited. In the case of transport measurements with capacitively induced carriers, the type I GaAs/AlGaAs band alignment makes it difficult to develop independent and selective contacts to the electron and hole layers. In addition, the energy separation between electron and hole states is ≈1.5 eV, requiring rather wide AlGaAs barriers to avoid interlayer leakage. As a consequence, the electron–hole mutual Coulomb attraction is relatively weak and exciton formation is greatly suppressed.

For these reasons, investigation of other solid-state systems that may overcome some limitations of double layers in GaAs, graphene and TMDs is of great interest. In this letter we propose as a candidate for electron–hole superfluidity and BEC, an alternative mass-imbalanced solid-state system: a lattice-matched strained Si/Ge bilayer embedded into a germanium-rich SiGe crystal. Holes are confined in a compressively strained Ge quantum well and electrons in a tensile strained Si quantum well, with no barrier in between. This is possible since the Si/Ge interface offers a type II band alignment^22,23,24, and thus electrons and holes can be kept separate but very close together. This enhances the strength of the electron–hole attraction while preventing unwanted recombination.

This alternative route is promising since Si and Ge heterostructures have reached maturity in the past decade. Si and Ge heterostructures have very low disorder, with carrier mobilities exceeding one million in both constituents of the bilayer: the 2D electron gas in Si/SiGe²⁵ and the 2D hole gas in Ge/SiGe²⁶. Furthermore, the carrier density may be tuned over orders of magnitude by leveraging on industrial gate-stack technology^27,28. This material system also integrates with advanced quantum technologies^29,30, including long-lived electron spin qubits in Si^31,32, hole spin qubit arrays in Ge^33,34 and superconducting contacts to holes^35,36,37. Two major advantages of the Si/Ge bilayer over the GaAs and TMD material systems are: (1) a quantum well for holes does not exist in the Si layer, and a quantum well for electrons is not energetically accessible in the Ge layer; this makes it much easier to electrically contact one layer and not the other, in contrast to the multi-stage processing required for independent contacts in GaAs and TMD systems; (2) the much smaller energy gap between electron and hole levels greatly facilitates the formation of equilibrium electron–hole systems without the need for large interlayer biases. Due to strain, there is a very large mass imbalance between holes in Ge (≈0.05 m_e)³⁸ and electrons in Si (≈0.19 m_e)^22,39, opening the door to exploration of exotic superfluid phases. Finally, these Si/Ge heterostructures may be grown on 300 mm Si wafers using mainstream chemical vapour deposition⁴⁰, and may profit from advanced semiconductor manufacturing for high device yield and integration.

Our calculations show that the envisaged Si/Ge bilayer supports a superfluid condensate. Tuning the carrier density, continuously sweeps the superfluid across the BEC and BCS–BEC regimes, with an accompanying variation in the magnitude of the superfluid gap and the transition temperature.

Results

Material stack and device architecture

Figure 1a illustrates the concept of a lattice-matched Si/Ge bilayer. A cubic (strain-relaxed) Ge-rich Si_1−xGe_x substrate, with a Ge concentration x = 0.8, sets the overall in-plane lattice parameter of the stack. For layer thicknesses below the critical thickness for onset of plastic relaxation, the Si/Ge epilayers will grow with the same in-plane lattice constants as the underlying Si_0.2Ge_0.8^41,42. Therefore, the Ge layer will be compressively strained in the in-plane direction⁴³ and, conversely, the Si layer will be under tensile strain²². A thickness of 3 nm for each Ge and Si layer allows for such strain engineering⁴², and is feasible experimentally given the recent advances in low-temperature chemical vapour deposition of SiGe heterostructures comprising Si and Ge quantum wells^43,44.

Fig. 1: Lattice-matched double Si/Ge bilayer, band structure, device architecture.

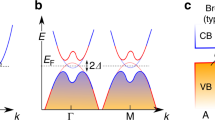
a Below the critical thickness for plastic relaxation, epitaxial Ge and Si layers are lattice matched to the underlying SiGe, with compressive and tensile strain, respectively. b Band structure of low-lying bands resulting in a double quantum well structure. Due to the type II band alignment at the strained Si/Ge heterojunction, electrons (Δ₂ states) are confined in tensile strained Si and holes (HH states) in compressively strained Ge. c Material stack with embedded Si/Ge bilayer and an envisaged device architecture, characterized by independent n⁺⁺ and p⁺⁺ contacts, and gate electrodes to tune independently the electron and hole densities in the bilayer.

Figure 1b shows the band structure of the proposed lattice-matched Si/Ge bilayer, where the Ge and Si layers are strained in opposite directions. The band structure was calculated in an effective mass approach using deformation potential theory to take into account the impact of the strain field on the relevant band edges. We highlight three highly attractive features. First, as already noted in the introduction, there is effectively only one quantum well for electrons spatially separated from the single quantum well for holes. There does exist a quantum well for electrons in Ge²⁴, but it is located so high in energy it would remain inactive for the present phenomenon. Thus the Si/Ge system is quite different from GaAs DQW²¹ and TMD heterostructures⁴⁵, where each of the two layers has both electron and hole wells, and also differs from GaAs/AlAs bilayers where the GaAs layer hosts both electron and hole bound states⁴⁶. The valence band profile shows that the wave function of the fundamental heavy hole (HH) state is confined in the Ge quantum well. The large energy splittings between the fundamental HH state and the fundamental light hole (LH) state are the result of the compressive strain and the larger confinement mass of the HH with respect to the LH. The conduction band profile shows that the wave function of the fundamental Δ₂ state is confined in the Si quantum well, with other states being higher up in energy. There is no hole quantum well in the Si layer. The second feature is that the energy difference between the bottom of the conduction band and the top of the valence band is ≈0.18 eV. This is ~8 times smaller than in GaAs quantum wells, meaning a small interlayer bias should be sufficient for tuning of the electron and hole wave-function shape and position in the quantum well. Finally, based on previous theoretical predictions and experiments, such strained Ge and Si quantum wells will result in a large imbalance of the masses, with a very light in-plane effective mass for holes (≈0.05 m_e) and a much heavier in-plane effective mass for electrons (≈0.19 m_e). This has important implications for the superfluid, as detailed in the subsection “Screening polarizabilities in the superfluid state”.

Figure 1c illustrates the entire material stack with the embedded Si/Ge bilayer and an envisaged device architecture. Starting from a Si(001) wafer and a thick strain-relaxed Ge layer deposited on top, a high-quality Si_0.2Ge_0.8 strain-relaxed buffer is obtained by reverse grading the Ge content in the alloy^43,47. Importantly, the strain-relaxed Si_0.2Ge_0.8 buffer can be heavily p-type doped to serve as an epitaxial bottom gate. This bottom gate can be biased negatively to populate only the undoped Ge quantum well with holes. Following the deposition of the Si/Ge bilayer, an additional Si_0.2Ge_0.8 barrier separates the Si quantum well from a dielectric layer and top gate. The top gate may be biased positively to populate only the undoped Si quantum well with electrons. Separate and independent Ohmic contacts to the capacitively induced 2D electron gas in Si and hole gas in Ge are achieved by standard n⁺⁺ and p⁺⁺ ion implantation, respectively^23,40. Alternatively, the p⁺⁺ contact may be substituted with an aluminium layer or an in-diffused metallic germano-silicide, as routinely done in Ge/SiGe heterostructure field effect transistors⁴³. By carefully designing the thickness of the Si_0.2Ge_0.8 barriers above and below the Si/Ge bilayer, we envisage that the carrier density may be tuned independently in the electron and hole layer in the low-density regime, n < 10¹¹ cm⁻².

Independent electrical contact to the two layers is easily achieved thanks to the remarkable and exceptional band structure of the material stack, with only one quantum well for electrons in the strained Si and only one accessible quantum well for holes in the strained Ge. Crucially, the prospect to make independent contacts to the electron–hole bilayer with a simple and robust process, in contrast to the challenging processing required for selective contacts in III–V and TMD materials, bodes well for superfluidity measurements in counterflow configurations^3,21.

Superfluid properties

In Fig. 2, we report superfluid properties of the system, calculated including self-consistent screening of the electron–hole pairing interaction. Self-consistent treatment of the long-ranged Coulombic pairing interaction⁴⁸ is a key element for determining electron–hole superfluid properties, in contrast to other superconductors and superfluids with short-range pairing interactions.

Fig. 2: Properties of the zero-temperature superfluid gap.

a Maximum of the gap ${{{\Delta }}}_{\max }$ as a function of the equal carrier densities n. The blue and yellow areas represent the BEC and BCS–BEC crossover regimes. The BCS regime is suppressed by screening. b Momentum dependent gap Δ_k at the three densities n indicated by the colour-coded dots on the curve in (a). c ${{{\Delta }}}_{\max }$ scaled by the electron and hole Fermi energies E_F,e and E_F,h.

Figure 2a shows the maximum of the zero-temperature superfluid gap ${{{\Delta }}}_{\max }$ as a function of the electron and hole densities, assumed equal. As the density n increases, ${{{\Delta }}}_{\max }$ first increases, passes through a maximum and then decreases. Above an onset density, n₀ ~ 5.9 × 10¹⁰ cm⁻², ${{{\Delta }}}_{\max }$ very rapidly drops to negligible values, ≲1 μeV. The behaviour of ${{{\Delta }}}_{\max }$ is a consequence of the self-consistency included in the screening¹⁰. This has radically different effects in the different regimes of the superfluidity^49,50. (1) At low carrier densities, the binding energy of the electron–hole pairs is large relative to the Fermi energy, and the excitons are strongly bound and compact. They resemble weakly interacting, approximately neutral, bosons and screening is negligible. (2) With increasing density, the number of pairs increases and the gap gets stronger. However, relative to the Fermi energy the gap gets weaker, and the superfluid moves from the BEC regime of bosons to the less strongly coupled BCS–BEC crossover regime of coupled fermionic pairs. (3) When the density is further increased above the onset density, n > n₀, strong screening overcomes the weak electron–hole pair coupling in what would be the BCS regime, and the superfluidity is suppressed.

The density ranges for the BEC and BCS–BEC crossover regimes are indicated in Fig. 2a by the blue and yellow shaded areas. We characterize the regimes by the condensate fraction parameter c, the fraction of carriers bound in pairs^51,52. The boundary between the BEC and BCS–BEC crossover regimes is determined by c = 0.8. The BCS–BEC crossover to BCS boundary would be located at c = 0.2, but at the onset density n₀ the condensate fraction has only dropped to c ~ 0.5, implying the absence of a BCS regime.

Figure 2b shows the momentum dependence of the superfluid gap Δ_k at three densities n. Near the onset density n₀ = 5.9 × 10¹⁰ cm⁻², which is in the BCS–BEC crossover regime, Δ_k has a broad peak centred close to k = k_F, indicating proximity of the BCS regime. At density n = 3.0 × 10¹⁰ cm⁻² corresponding to the maximum of ${{{\Delta }}}_{\max }$, which is near the boundary separating the BCS–BEC crossover and BEC regimes, the peak in Δ_k has moved back to k = 0. At n = 0.5 × 10¹⁰ cm⁻², which is in the deep BEC regime, Δ_k extends out to large k/k_F.

Figure 2c shows ${{{\Delta }}}_{\max }$ scaled to the electron and hole Fermi energies. At the onset density, while ${{{\Delta }}}_{\max }<{E}_{{\rm{F}},{\rm{h}}}$, it is surprising that ${{{\Delta }}}_{\max }\gg {E}_{{\rm{F}},{\rm{e}}}$. This result significantly differs from the equal mass case, for which the onset density occurs around ${{{\Delta }}}_{\max }/{E}_{{\rm{F}},{\rm{h}}}={{{\Delta }}}_{\max }/{E}_{{\rm{F}},{\rm{e}}} \sim 1$. We recall the physical argument that a sufficiently strong energy gap ${{{\Delta }}}_{\max }$ relative to the Fermi energy will exclude from the screening low-lying excited states that otherwise would very significantly weaken the electron–hole attraction⁴⁹. But it is puzzling why ${{{\Delta }}}_{\max }$ must become so much larger than E_F,e before the screening is suppressed by the superfluidity. To explain this, we must look at the self-consistent screening polarizabilities in the superfluid state when the electron and hole masses are unequal.

Screening polarizabilities in the superfluid state

We now examine the effect of the different masses on the polarizabilities that control the self-consistent screening. Figure 3 shows the normal polarizabilities for electrons and holes in the presence of the superfluid, Π_e(q) and Π_h(q) (Eqs. (8) and (9)), and the anomalous polarizability for the superfluid electron–hole pairs, Π_a(q) (Eq. (10)). The panels are for two densities, the first close to the onset density in the BCS–BEC crossover regime and the second in the BEC regime.

Fig. 3: Polarizabilities.

The green (blue) solid lines are the normal electron (hole) polarizabilities in the presence of the superfluid Π_e(q) (Π_h(q)). The red solid lines are the anomalous polarizabilities Π_a(q) for the superfluid electron–hole pairs. Dashed green and blue lines are the corresponding effective polarizabilities ${{{\Pi }}}_{{\rm{e}},{\rm{h}}}^{{\rm{eff}}}({\bf{q}})\equiv {{{\Pi }}}_{{\rm{e}},{\rm{h}}}({\bf{q}})+{{{\Pi }}}_{{\rm{a}}}({\bf{q}})$. a For density n ≃ n₀ = 5.9 × 10¹⁰ cm⁻² in the BCS–BEC crossover regime. b For density n = 0.5 × 10¹⁰ cm⁻² in the BEC regime.

If the effect of the superfluidity on the screening is not taken into account, the polarizabilities in the normal state would be much larger than Π_e(q) and Π_h(q). In 2D, they would be given in the momentum transfer range relevant for screening q/k_F ≤ 2, by their respective densities of states:

$$\begin{array}{l}{{{\Pi }}}_{{\rm{e}}}^{{\rm{(NS)}}}({\bf{q}})=\frac{{m}_{{\rm{e}}}^{\star }}{{\rm{\pi }}{\hslash }^{2}}\simeq 8.0\times 1{0}^{10}\ {\text{cm}}^{-2}{\text{meV}}^{-1},\\ {{{\Pi }}}_{{\rm{h}}}^{{\rm{(NS)}}}({\bf{q}})=\frac{{m}_{{\rm{h}}}^{\star }}{{\rm{\pi }}{\hslash }^{2}}\simeq 2.1\times 1{0}^{10}\ {\text{cm}}^{-2}{\text{meV}}^{-1}.\end{array}$$

(1)

Such large polarizabilities would lead to very strong screening of the electron–hole interaction, resulting in extremely weak-coupled superfluidity and very low transition temperatures in the mK range⁴⁹. The suppression of the normal polarizabilities in the superfluid state arises from the blocking by the superfluid gap of low-lying states in the energy spectrum (Eqs. (8) and (9)). There is even more suppression of screening that comes from cancellation with the anomalous polarizability in the screened interaction (Eq. (11)). To highlight these cancellations, in Fig. 3 we introduce effective polarizabilities, ${{{\Pi }}}_{{\rm{e}}}^{{\rm{eff}}}({\bf{q}})={{{\Pi }}}_{{\rm{e}}}({\bf{q}})+{{{\Pi }}}_{{\rm{a}}}({\bf{q}})$ and ${{{\Pi }}}_{{\rm{h}}}^{{\rm{eff}}}({\bf{q}})={{{\Pi }}}_{{\rm{h}}}({\bf{q}})+{{{\Pi }}}_{{\rm{a}}}({\bf{q}})$.

At q = 0 and for all densities, there is the property Π_e(q = 0) = Π_h(q = 0) = − Π_a(q = 0), so that ${{{\Pi }}}_{{\rm{e}}}^{{\rm{eff}}}({\bf{q}}\ =\ 0)={{{\Pi }}}_{{\rm{h}}}^{{\rm{eff}}}({\bf{q}}\ =\ 0)=\ 0$, reflecting the absence of long distance screening for any non-zero superfluid gap. For non-zero q, however, the cancellation of polarizabilities and the suppression of screening are very sensitive to which regime the superfluidity lies in. Δ_k becomes narrower as we move from the BEC regime, across the BCS–BEC crossover regime, and towards the BCS regime (Fig. 2b), narrowing both the momentum range for blocked excitations and the momentum range for which the cancellations are significant.

Figure 3a is in the BCS–BEC crossover regime, where we see that the behaviour of Π_e(q) for non-zero q is strikingly different from Π_h(q). Further details of their differences in functional behaviour can be found in the Supplementary Discussion of Supplementary Fig. 1. We also note the approximate cancellation of Π_a(q) with Π_h(q) but not with Π_e(q). This is because Π_a(q) depends on the strength of the pairing, and so scales with the reduced mass ${m}_{{\rm{r}}}^{\star }$, which for this system is approximately equal to ${m}_{{\rm{h}}}^{\star }$. In contrast ${m}_{{\rm{r}}}^{\star }\ll {m}_{{\rm{e}}}^{\star }$, so |Π_e(q)| is larger than Π_a(q) and does not cancel with it. We conclude for intermediate values of k/k_F, that Δ_k strongly suppresses the effective polarization for holes, ${{{\Pi }}}_{{\rm{h}}}^{{\rm{eff}}}({\bf{q}})$, but does not suppress the effective polarization for electrons, ${{{\Pi }}}_{{\rm{e}}}^{{\rm{eff}}}({\bf{q}})$. This explains the puzzling result we noted in Fig. 2c, that the screening is only suppressed when the gap reaches very large values of ${{{\Delta }}}_{\max }/{E}_{{\rm{F}},{\rm{e}}}\gg 1$.

In contrast, Fig. 3b shows in the deep BEC regime for q/k_F ≲ 2 that Π_e(q) and Π_h(q) are very similar and now both scale with the reduced mass ${m}_{{\rm{r}}}^{\star }$, like Π_a(q). This is because in this regime the electrons and holes are in strongly bound pairs that have lost their single-particle character. As a result, ${{{\Pi }}}_{{\rm{e}}}^{{\rm{eff}}}({\bf{q}})$ and ${{{\Pi }}}_{{\rm{h}}}^{{\rm{eff}}}({\bf{q}})$ are very small over the momentum transfer range important for screening, reflecting near complete cancellation. Physically, the electron–hole pairs in the deep BEC are compact compared with the inter-particle spacing and approximately neutral, and this makes screening unimportant.

Superfluid phase diagram

The superfluid transition for a 2D system is a Berezinskii–Kosterlitz–Thouless (BKT) transition⁵³. For parabolic bands, the transition temperature ${T}_{\rm{c}}^{{\rm{BKT}}}$ becomes linearly proportional to the carrier density n (Eq. (14)). The highest transition temperature occurs at the onset density. The complete phase diagram is shown in Fig. 4. Despite the large dielectric constant and the small hole mass, we see that the transition temperatures are readily experimentally accessible, up to ${T}_{\rm{c}}^{{\rm{BKT}}}=2.5$ K.

Fig. 4: Phase diagram.

${T}_{\rm{c}}^{{\rm{BKT}}}$ is the superfluid transition temperature. n is the density of the electrons and holes. T_d is the degeneracy temperature for the exciton gas. The superfluid BEC and BCS–BEC crossover regimes are indicated. Above n ~ 6 × 10¹⁰ cm⁻², the superfluid transition temperature is in the mK range.

At ${T}_{\rm{c}}^{{\rm{BKT}}}$, there is a thermally driven transition to a degenerate exciton gas, in which the system has lost its macroscopic coherence but local pockets of superfluidity remain. These pockets persist up to a characteristic degeneracy temperature T_d⁵⁴. At T_d, the excitons lose degeneracy and the system becomes a classical exciton gas.

When the density is increased to an onset density n₀ = 5.9 × 10¹⁰ cm⁻², the superfluid gap drops nearly discontinuously to exponentially small values (Fig. 2a), and ${T}_{\rm{c}}^{{\rm{BKT}}}$ drops to the sub-mK range. The drop in the gap is similar to a first-order transition, and is caused by the sudden collapse of three solutions to the gap equation (Eq. (6)) into a single very low-energy solution⁴⁸. This is caused by strong screening of the electron–hole pairing attraction.

Discussion

In summary, we predict superfluidity in experimentally accessible samples, densities and temperatures, with a superfluid gap of up to 3 meV and a transition temperature up to 2.5 K. At carrier densities higher than 6 × 10¹⁰ cm⁻², the relatively weak superfluidity is unable to suppress the increasingly strong screening, with a result that screening suppresses superfluidity. The nature of this self-consistent screening process is sensitive to the system property that the electron and hole masses are markedly different. Since the existence of exotic superfluid phases is dependent on unequal masses, and because the effect of unequal masses does not manifest itself in the BEC regime (n ≤ 2 × 10¹⁰ cm⁻²), the experimental search for these exotic phases should focus on intermediate densities in the BCS–BEC crossover regime (2 × 10¹⁰ < n < 6 × 10¹⁰ cm⁻²).

In a realistic implementation of the proposed Si/Ge bilayer material stack, the Si/Ge interface will have a finite width due to segregation, diffusion and intermixing associated with the chemical vapour deposition. However, by depositing the Si/Ge layers at sufficiently low temperatures (≤500 °C as in Refs. ^43,44), we foresee a distance for transitioning between the strained Ge and Si layer of much less of 1 nm. The details of such Si/Ge transition region do not influence the main findings of the band structure calculations nor the superfluid properties, since the principle parameter affecting these is the distance separating the centres of the two wells.

The superfluid gap shown in Fig. 2a reaches 35 K (3 meV), and the transition temperature could be increased up to a significant fraction of this value by implementing variations of the proposed Si/Ge material stack, for example, by including a finite stack of bilayers that eliminates the limitations of a 2D system⁵⁵. Such Si/Ge material stacks with up to five bilayers are within reach, considering the recent experimental progress in the deposition of multi-quantum wells on Ge-rich SiGe virtual substrates⁵⁶. In this way, the transition temperature would allow for the design and development of an entire original class of dissipationless logic devices and electronics⁵⁷ for CMOS-based cryogenic control of silicon quantum circuits⁵⁸.

Methods

For calculations of the superfluid properties, we take a structure with hole effective mass ${m}_{{\rm{h}}}^{\star }=0.05\ {m}_{{\rm{e}}}$ in the compressively strained Ge layer, and electron effective mass ${m}_{{\rm{e}}}^{\star }=0.19\ {m}_{{\rm{e}}}$ in the tensile strained Si layer. We use a uniform dielectric constant determined for Si and Ge quantum wells of equal width in contact, $\epsilon =2{\left(1/{\epsilon }_{{\rm{Ge}}}+1/{\epsilon }_{{\rm{Si}}}\right)}^{-1}=13.7\ {\epsilon }_{0}$, with ϵ_Ge = 16.2 ϵ₀ and ϵ_Si = 11.9 ϵ₀. Lengths are expressed in units of the effective Bohr radius, ${a}_{{\rm{B}}}^{\star }={\hslash }^{2}4{\rm{\pi }}\epsilon /({m}_{{\rm{r}}}^{\star }{e}^{2})=18.3$ nm, and energies in effective Rydbergs, ${{\rm{Ry}}}^{\star }={e}^{2}/(2{a}_{{\rm{B}}}^{\star })=33$ K. ${m}_{{\rm{r}}}^{\star }$ is the reduced effective mass.

Mean-field equations

Because of the different masses, there are distinct electron and hole normal Matsubara Green functions:

$$\begin{array}{l}{G}_{{\rm{e}}}({\bf{k}},\tau )=-\left\langle {T}_{\tau }\ c({\bf{k}},\tau ){c}^{\dagger }({\bf{k}},0)\right\rangle ,\\ {G}_{{\rm{h}}}({\bf{k}},\tau )=-\left\langle {T}_{\tau }\ d({\bf{k}},\tau ){d}^{\dagger }({\bf{k}},0)\right\rangle .\end{array}$$

(2)

T_τ is the ordering operator in imaginary time τ. c^† and c (d^† and d) are the creation and destruction operators for electrons (holes) in their respective quantum wells. The corresponding anomalous Green function is as follows:

$$F({\bf{k}},\tau )=-\left\langle {T}_{\tau }\ c({\bf{k}},\tau )d({\bf{k}},0)\right\rangle \ .$$

(3)

In the weak-coupling BCS limit, Eqs. (2) and (3) reduce to:

$$\begin{array}{l}{G}_{{\rm{e}}}({\rm{i}}{\omega }_{{n}},{\bf{k}})=\frac{{u}_{{\bf{k}}}^{2}}{({\rm{i}}{\omega }_{{n}}\,-\,{E}_{{\bf{k}}}^{-})}+\frac{{v}_{{\bf{k}}}^{2}}{({\rm{i}}{\omega }_{{n}}\,+\,{E}_{{\bf{k}}}^{+})},\\ {G}_{{\rm{h}}}({\rm{i}}{\omega }_{{n}},{\bf{k}})=\frac{{v}_{{\bf{k}}}^{2}}{({\rm{i}}{\omega }_{{n}}\,+\,{E}_{{\bf{k}}}^{-})}+\frac{{u}_{{\bf{k}}}^{2}}{({\rm{i}}{\omega }_{{n}}\,-\,{E}_{{\bf{k}}}^{+})},\\ F({\rm{i}}{\omega }_{{n}},{\bf{k}})\;\;=\frac{{u}_{{\bf{k}}}{v}_{{\bf{k}}}}{({\rm{i}}{\omega }_{{n}}\,-\,{E}_{{\bf{k}}}^{-})}-\frac{{u}_{{\bf{k}}}{v}_{{\bf{k}}}}{({\rm{i}}{\omega }_{{n}}\,+\,{E}_{{\bf{k}}}^{+})},\end{array}$$

(4)

where ω_n (n = 1, 2, 3… ) are the fermionic Matsubara frequencies and

$${E}_{{\bf{k}}}^{\pm }={E}_{{\bf{k}}}\pm \delta {\xi }_{{\bf{k}}}\ ,\quad {E}_{{\bf{k}}}=\sqrt{{\xi }_{{\bf{k}}}^{2}+{{{\Delta }}}_{{\bf{k}}}^{2}}\ ,\quad \delta {\xi }_{{\bf{k}}}=\frac{1}{2}\left({\xi }_{{\bf{k}}}^{{\rm{h}}}-{\xi }_{{\bf{k}}}^{{\rm{e}}}\right)\ ,\quad {\xi }_{{\bf{k}}}=\frac{1}{2}\left({\xi }_{{\bf{k}}}^{{\rm{e}}}+{\xi }_{{\bf{k}}}^{{\rm{h}}}\right).$$

(5)

${\xi }_{{\bf{k}}}^{{\rm{e}}}=\frac{{k}^{2}}{2{m}_{{\rm{e}}}^{\star }}-\mu$ (${\xi }_{{\bf{k}}}^{{\rm{h}}}=\frac{{k}^{2}}{2{m}_{{\rm{h}}}^{\star }}-\mu$) is the electron (hole) single-particle energy band dispersion in the normal state, with μ the chemical potential. Δ_k is the superfluid energy gap. The Bogoliubov amplitudes are ${u}_{{\bf{k}}}^{2}=\frac{1}{2}\left(1+\frac{{\xi }_{{\bf{k}}}}{{E}_{{\bf{k}}}}\right)$ and ${v}_{{\bf{k}}}^{2}=\frac{1}{2}\left(1-\frac{{\xi }_{{\bf{k}}}}{{E}_{{\bf{k}}}}\right)$.

We consider only equal electron and hole densities n. At zero temperature, the superfluid energy gap can be determined from the usual mean-field equation of BCS theory, even in the strongly interacting BCS–BEC crossover and BEC regimes:

$${{{\Delta }}}_{{\bf{k}}}=\frac{1}{{L}^{2}}\ \mathop{\sum}\limits_{{\bf{k}}^{\prime} ,{\omega }_{{n}}}\ \ {V}_{{\bf{k}}-{\bf{k}}^{\prime} }^{{\rm{sc}}}F(i{\omega }_{{n}},{\bf{k}}^{\prime} )\ =\ -\frac{1}{{L}^{2}}\ \mathop{\sum}\limits_{{\bf{k}}^{\prime} }\ {V}_{{\bf{k}}-{\bf{k}}^{\prime} }^{{\rm{sc}}}\frac{{{{\Delta }}}_{{\bf{k}}^{\prime} }}{2{E}_{{\bf{k}}^{\prime} }},$$

(6)

where ${V}_{{\bf{k}}-{\bf{k}}^{\prime} }^{{\rm{sc}}}={V}_{{\bf{q}}}^{{\rm{sc}}}$ is the attractive screened electron–hole interaction. As expected, the only mass parameter entering in Eq. (6) is the reduced mass ${m}_{{\rm{r}}}^{\star }$. Equation (6) is self-consistently solved coupled to the density equation:

$$n=\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}},{\omega }_{{n}}}{G}_{{\rm{\ell }}}({\rm{i}}{\omega }_{{n}},{\bf{k}})=\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}}}{v}_{{\bf{k}}}^{2}\quad {\rm{\ell }}={\rm{e}},{\rm{h}}.$$

(7)

For given density n, Eq. (7) determines the chemical potential μ.

Self-consistent screening

Because the electron–hole interaction is Coulombic and long ranged, it is essential to include screening in ${V}_{{\bf{q}}}^{{\rm{sc}}}$. To determine the screening in the presence of a superfluid, we evaluate the density response functions within the random-phase approximation for the DQW system in which the electrons and holes have different masses²⁰. For the polarization loops, we use the normal and anomalous Green functions, Eq. (4). Then the normal polarizabilities in the presence of the superfluid are as follows:

$$\begin{array}{l}{{{\Pi }}}_{{\rm{e}}}({\bf{q}})=\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}}}\mathop{\sum}\limits_{{\omega }_{{n}}}{G}_{{\rm{e}}}({\rm{i}}{\omega }_{{n}},{\bf{k}}){G}_{{\rm{e}}}({\rm{i}}{\omega }_{{n}},{\bf{k}}-{\bf{q}})\\ \qquad\;\;\; =-\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}}}\left[\frac{{u}_{{\bf{k}}}^{2}{v}_{{\bf{k}}-{\bf{q}}}^{2}}{{E}_{{\bf{k}}-{\bf{q}}}^{+}\,+\,{E}_{{\bf{k}}}^{-}}+\frac{{v}_{{\bf{k}}}^{2}{u}_{{\bf{k}}-{\bf{q}}}^{2}}{{E}_{{\bf{k}}-{\bf{q}}}^{-}\,+\,{E}_{{\bf{k}}}^{+}}\right],\end{array}$$

(8)

$$\begin{array}{l}{{{\Pi }}}_{{\rm{h}}}({\bf{q}})=\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}}}\mathop{\sum}\limits_{{\omega }_{{n}}}{G}_{{\rm{h}}}({\rm{i}}{\omega }_{{n}},{\bf{k}}){G}_{{\rm{h}}}({\rm{i}}{\omega }_{{n}},{\bf{k}}-{\bf{q}})\\ \qquad\;\,\;\;=-\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}}}\left[\frac{{u}_{{\bf{k}}}^{2}{v}_{{\bf{k}}-{\bf{q}}}^{2}}{{E}_{{\bf{k}}-{\bf{q}}}^{-}\,+\,{E}_{{\bf{k}}}^{+}}+\frac{{v}_{{\bf{k}}}^{2}{u}_{{\bf{k}}-{\bf{q}}}^{2}}{{E}_{{\bf{k}}-{\bf{q}}}^{+}\,+\,{E}_{{\bf{k}}}^{-}}\right].\end{array}$$

(9)

The anomalous polarizability for the density response of the superfluid electron–hole pairs is as follows:

$$\begin{array}{l}{{{\Pi }}}_{a}({\bf{q}})=\frac{2}{{L}^{2}}\mathop{\sum}\limits_{{\bf{k}}}\mathop{\sum}\limits_{{\omega }_{{n}}}F({\rm{i}}{\omega }_{{n}},{\bf{k}})F({\rm{i}}{\omega }_{{n}},{\bf{k}}-{\bf{q}})\\ \qquad\;\;\;\,=\frac{2}{{L}^{2}}\ \mathop{\sum}\limits_{{\bf{k}}}\frac{{{{\Delta }}}_{{\bf{k}}}}{2{E}_{{\bf{k}}}}\frac{{{{\Delta }}}_{{\bf{k}}-{\bf{q}}}}{2{E}_{{\bf{k}}-{\bf{q}}}}\ \left[\ \frac{1}{{E}_{{\bf{k}}-{\bf{q}}}^{-}\ +\ {E}_{{\bf{k}}}^{+}}\ +\ \frac{1}{{E}_{{\bf{k}}-{\bf{q}}}^{+}\ +\ {E}_{{\bf{k}}}^{-}}\ \right].\end{array}$$

(10)

For Δ_k ≡ 0, the Π_e(q) and Π_h(q) reduce to the usual Lindhard functions of the normal state, and Π_a(q) vanishes.

The expression for the static screened electron–hole interaction for unequal masses is as follows:

$${V}_{{\bf{q}}}^{{\rm{sc}}}=\frac{{V}_{{\bf{q}}}^{{\rm{eh}}}}{1-[{{{\Pi }}}_{{\rm{e}}}({\bf{q}}){V}_{{\bf{q}}}^{{\rm{ee}}}+{{{\Pi }}}_{{\rm{h}}}({\bf{q}}){V}_{{\bf{q}}}^{{\rm{hh}}}]+2{V}_{{\bf{q}}}^{{\rm{eh}}}{{{\Pi }}}_{{\rm{a}}}({\bf{q}})+[{V}_{{\bf{q}}}^{{\rm{ee}}}{V}_{{\bf{q}}}^{{\rm{hh}}}-{({V}_{{\bf{q}}}^{{\rm{eh}}})}^{2}][{{{\Pi }}}_{{\rm{e}}}({\bf{q}}){{{\Pi }}}_{{\rm{h}}}({\bf{q}})-{{{\Pi }}}_{{\rm{a}}}^{2}({\bf{q}})]}.$$

(11)

${V}_{{\bf{q}}}^{{\rm{ee}}}$ (${V}_{{\bf{q}}}^{{\rm{hh}}}$) is the bare electron (hole) Coulomb repulsion within one quantum well, and ${V}_{{\bf{q}}}^{{\rm{eh}}}$ is the bare attraction between the electrons and holes in opposite quantum wells:

$${V}_{{\bf{q}}}^{{\rm{ee}}}=\frac{2{\rm{\pi }}{e}^{2}}{\epsilon }\frac{1}{| {\bf{q}}| }{{\mathcal{F}}}_{{\bf{q}}}^{{\rm{ee}}};\quad {V}_{{\bf{q}}}^{{\rm{hh}}}=\frac{2{\rm{\pi }}{e}^{2}}{\epsilon }\frac{1}{| {\bf{q}}| }{{\mathcal{F}}}_{{\bf{q}}}^{{\rm{hh}}};\quad {V}_{{\bf{q}}}^{{\rm{eh}}}=-\frac{2{\rm{\pi }}{e}^{2}}{\epsilon }\frac{{{\rm{e}}}^{-{d}_{{\rm{c}}}| {\bf{q}}| }}{| {\bf{q}}| }{{\mathcal{F}}}_{{\bf{q}}}^{{\rm{eh}}}.$$

(12)

We take for the separation parameter d_c the distance between the centre of the two wells. The form-factors ${{\mathcal{F}}}_{{\bf{q}}}$ account for the density distribution of the electrons and holes within their respective finite-width wells⁵⁹.

We self-consistently solve the superfluid gap equation (Eq. (6)), the density equation (Eq. (7)) and the screened interaction in the presence of the superfluid (Eq. (11)) iteratively, calculating the polarizabilities (Eqs. (8)–(10)) using the superfluid gaps determined in the preceding iteration.

Transition temperature

The superfluid transition temperature in this quasi-2D system is determined as a BKT transition⁵³. For parabolic bands the transition temperature ${T}_{{c}}^{{\rm{BKT}}}$ is well approximated by⁶⁰:

$${T}_{\rm{c}}^{{\rm{BKT}}}=\frac{{\rm{\pi }}}{2}{\rho }_{{\rm{s}}}({T}_{\rm{c}}^{{\rm{BKT}}}).$$

(13)

Within mean-field theory the superfluid stiffness at zero temperature ${\rho }_{{\rm{s}}}(0)={\hslash }^{2}n/8{m}_{{\rm{r}}}^{\star }$ depends only on the carrier density n, independent of the pair coupling strength. We are able to neglect the temperature dependence of ρ_s(T) in Eq. (13) since ρ_s(T) is approximately constant for temperatures $T\ll {{{\Delta }}}_{\max }$. Thus the transition temperature is linearly proportional to the carrier density:

$${T}_{\rm{c}}^{{\rm{BKT}}}=\frac{{\hslash }^{2}}{16{m}_{{\rm{r}}}^{\star }}{\rm{\pi }}n.$$

(14)