Abstract
The existence of a nematic phase transition in iron-chalcogenide superconductors poses an intriguing question about its impact on superconductivity. To understand the nature of this unique quantum phase transition, it is essential to study how the electronic structure changes across this transition at low temperatures. Here, we investigate the evolution of the Fermi surfaces and electronic interactions across the nematic phase transition of FeSe1−xSx using Shubnikov-de Haas oscillations in high magnetic fields up to 45 T in the low temperature regime down to 0.4 K. Most of the Fermi surfaces of FeSe1−xSx monotonically increase in size except for a prominent low frequency oscillation associated with a small, but highly mobile band, which disappears at the nematic phase boundary near x ~ 0.17, indicative of a topological Lifshitz transition. The quasiparticle masses are larger inside the nematic phase, indicative of a strongly correlated state, but they become suppressed outside it. The experimentally observed changes in the Fermi surface topology, together with the varying degree of electronic correlations, will change the balance of electronic interactions in the multi-band system FeSe1−xSx and promote different kz-dependent superconducting pairing channels inside and outside the nematic phase.
Similar content being viewed by others
Introduction
Nematic electronic order is believed to play an important role in the phenomenology of superconductivity in iron-based and copper oxide superconductors.1,2 FeSe is an ideal system to study nematicity, in the absence of long-range magnetism, which manifests itself in substantial distortions of the Fermi surfaces,3,4 as well as a strong twofold anisotropy, detected in quasiparticle interference spectra.5 The superconducting state of FeSe emerging around 9 K from this electronic nematic state is characterised by a highly anisotropic gap structure.5 However, the suppression of nematicity and the presence of magnetism can be a prerequisite for higher critical temperatures, Tc, found under applied pressure, intercalation or by surface doping.6,7,8
A clean route to investigate the interplay between nematicity, magnetism and superconductivity in FeSe is using chemical pressure-induced by isoelectronic substitution of selenium with sulphur in FeSe1−xSx, which suppresses both the nematic phase transition temperature and its related electronic anisotropies.9,10 Naively, chemical pressure could mimic the effect of applied hydrostatic pressure by bringing the FeSe layers closer together, increasing the bandwidth and suppressing the electronic correlations towards FeS, as found recently by angle resolved photoemission spectroscopy (ARPES).11 However, chemical pressure in FeSe1−xSx does not stabilize a magnetic order or enhance superconductivity, in contrast with the complex phase diagram of FeSe under applied pressure.12,13,14,15 Furthermore, combining physical and chemical pressures, the effect of nematicity and magnetism on superconductivity can be disentangled.16 Thus, identifying the evolution of the electronic structure of FeSe under different tuning parameters can provide important insights into the influence of nematic order on superconductivity.
In this paper, we use quantum oscillations detected in high quality single crystals of FeSe1−xSx to probe in detail the evolution of the multiband Fermi surfaces and quasiparticle properties across the nematic quantum phase transition at very low temperatures and high magnetic fields. We find that the sizes of the largest Fermi surface orbits increase with chemical pressure, as the degree of in-plane anisotropy is reduced. Furthermore, with increasing sulphur substitution we detect the appearance of a prominent low-frequency oscillation arising from a small high-mobility band which disappears together with the nematic phase. This suggests the presence of a Lifshitz transition caused by a topological change of the Fermi surface, not detected previously by spectroscopic probes. The effective masses of the outer hole band with dxz/yz character evolve smoothly across the nematic phase boundary, without any divergence at the critical doping, and follow similar trends to superconductivity across the phase diagram.
Results
Quantum oscillations in FeSe1−xSx
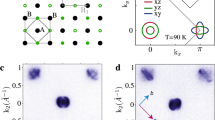
Figure 1 shows resistivity measurements of FeSe1−xSx with the magnetic field either perpendicular to the structural ab layers (θ = 0°) or tilted away by an angle (θ = 30°). In order to access the normal state at low temperatures the measurements are performed above the upper critical field; we find that Bc2 reaches a maximum of about 20 T for x ~ 0.07(1) with \(B||c\). In the normal state of FeSe1−xSx, complex Shubnikov-de Haas oscillations are superimposed on the magnetoresistance signal, being most prominent at the lowest temperatures and highest magnetic fields (see also Supplementary Fig. S2). The form of the oscillations varies significantly with the chemical pressure (Fig. 1a–f), indicating non-trivial evolution of the electronic structure. One striking observation is the emergence of a low-frequency oscillation (labelled λ in Fig. 1), which is observed prominently in the magnetoresistance from x ~ 0.012, but completely disappears outside the nematic phase at x ~ 0.17. This effect is better visualized in the first derivative of magnetoresistance plotted in Fig. 1g–k, which shows that the period of the oscillations becomes longer, thus the corresponding frequency become smaller with x, until it disappears close to x = 0.17, which corresponds to the nematic phase boundary, indicating that an extremal area of the Fermi surface disappears outside the nematic phase.
Quantum oscillations in superconducting single crystals of FeSe1−xSx. a–f The in-plane resistance Rxx(B) as a function of magnetic field B for different compositions, x, and nematic transition temperatures, Ts (defined in Supplementary Fig. S1b). Measurements were performed at constant temperatures (between 0.3 and 2 K) by sweeping the magnetic fields up to 45 T with B||c axis (θ = 0°) or θ = 30°. g–k The oscillatory part of the resistivity visualized better by the first derivative of resistance as a function of magnetic field from a–f at the lowest measured temperature. The horizontal line indicates the period of the low-frequency oscillations (~1/λ). l–p The frequency spectra of the oscillatory signal Δρosc/ρ obtained using a fast Fourier transform (FFT). A multiplied FFT spectrum is used to emphasize the weak high frequency features with their positions indicated by vertical arrows. r The proposed Fermi surface and the different extremal areas for FeSe1−xSx obtained by shrinking the calculated tetragonal Fermi surface (Supplementary Fig. S6). Frequencies below 200 T cannot be reliably assigned due to a possible overlap of at least 3 different small frequencies (α1, α2 and β)
Next we focus on fast Fourier transform (FFT) spectra, which helps us to identify the extremal areas of the Fermi surfaces normal to the applied magnetic field, Aki, given by the Onsager relation, Fi = Akiℏ/(2πe). For quasi-2D cylindrical Fermi surfaces, two extremal orbits contribute to the quantum oscillation signal, originating from the maximal and minimal areas.17 The low-temperature experimental Fermi surface of FeSe is composed of one warped cylindrical hole band and two electron bands with distorted areas, as sketched in Fig. 2e, f.3,18,19,20 For example, previous work has identified the β (kz = 0) and δ (kz = π/c) frequencies as the minimal and maximal orbits of the outer hole pocket,3,18,21 shown in Fig. 1r. Figure 1l–p shows the FFT spectra for the different compositions x. These may be separated into a high frequency region, originating from the largest Fermi surface areas of the outer electron γ and hole band δ,3,20 which increase with x up to 1.2 kT, and the low frequency region (below 0.4 kT) characterised by the superposition of oscillatory signals originating from small pockets of the Fermi surface of FeSe1−xSx, as shown in Fig. 1r.9,11 As a function of increasing chemical pressure, the sizes of the largest extremal areas expand; this trend is followed not only inside the nematic state, as the in-plane anisotropy is reduced, but also outside the nematic phase (Fig. 1l–p). This implies that the nematic phase does not cause Fermi surface reconstruction, as expected since nematic order breaks rotational but not translational symmetry. The orbits associated to the electron bands are separated by the spin-orbit coupling into outer flower-shape orbits (γ and ε) and inner orbits (α1 and α2) (Fig. 1r). Electron pockets are prone to further topological changes induced by the strength of the orbital order that pushed the inner electron band above the Fermi level, as found for FeSe films,22 and represented schematically in Fig. 2e (for x = 0). However, in FeSe1−xSx, as orbital order is suppressed,9 the quantum oscillations orbits of the electron bands most likely originate from the outer flower-shape and inner electron orbits (shown in Fig. 2e, f), similar to LiFe(As/P),23 BaFe2(As/P)224,25 and LaFePO.26 An additional frequency can occur when the inner hole pocket (χ in Fig. 1r), crosses the Fermi level by x = 0.11 to create a 3D Fermi pocket and its size increases with x, according to ARPES measurements.9,11 Thus, the subsequent disappearance of the low-frequency oscillations, λ, is unexpected and indicates a different provenance.
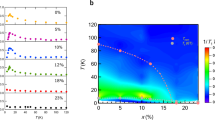
Quasiparticle effective masses and the angular dependence of quantum oscillations. Temperature dependence of the Fourier transform (FFT) amplitude of different frequencies for two different compositions, a x ~ 0.04 with Ts ~ 80 K and b x ~ 0.19 outside the nematic phase. c, d The effective masses extracted using a Lifshitz-Kosevich (LK) formula51 (solid line) indicating lighter quasiparticles masses outside the nematic phase. The angular dependence of the FFT amplitudes for e x ~ 0.04 and f x ~ 0.19 with an enhanced high frequency amplitude around θ ~ 30°. g Angular dependence of magnetoresistance of x ~ 0.17 as a function θ, the angle of the applied magnetic field with respect to the c-axis at 0.36 K (colour bar represents θ) and h quantum oscillations spectra (by subtracting a second order polynomial) for x ~ 0.17 indicating the quasi-two-dimensional nature of the observed low frequency pocket. The data in h are offset for clarity and the measured angle is indicated on the vertical axis
Quasiparticle effective masses of FeSe1−xSx
A direct manifestation of the effect of electron–electron interactions is the relative enhancement of the quasiparticle effective masses compared to the bare band masses. The cyclotron-averaged effective masses of the quasiparticles for each extremal orbit can be extracted from the temperature dependence of the amplitude of the quantum oscillations,17 as shown in Fig. 3a–d and Supplementary Fig. S5. For low substitution x ~ 0.04, the values of the effective masses are close to those reported for FeSe;18,27 the β and δ orbits corresponding to the outer hole band have similar effective masses ~4.3(1)me, indicating that they originate from the same cylindrical Fermi surface with dominant dxz/dxz band character. The γ and ε orbits (Fig. 1l, r) are likely to correspond to the outer electron band with dominant dxy band character, which has a particularly heavy mass of ~7(1)me, confirming the strong orbitally dependent band renormalization found in ARPES studies.3 In addition, the FFT spectrum includes a low frequency at 135 T with a lighter mass around ~3me21 corresponding to the inner electron band (α1 and/or α2 in Figs. 1r and 2c). However, we caution that the analysis of the lowest frequencies by FFT can be affected by the choice of polynomial background subtraction as well as 1/f noise.
Evolution of the electronic properties of FeSe1−xSx. a Phase diagram of FeSe1−xSx as a function of sulphur substitution, x indicating the suppression of the nematic phase (Ts, solid triangles) and the presence of a small dome of superconductivity (Tc, solid circles) using data from Supplementary Fig. S1. b Proposed phase diagram of FeSe under pressure based on ref. 7 showing the low Tc (SC1) and high Tc superconducting phases (SC2) as well as the magnetic phase. c The evolution of the observed quantum oscillations frequencies. Solid lines are the calculated frequencies for the large outer hole band based on ARPES data from ref. 9. The dashed lines are guides to the eye. d The quasiparticle effective masses of the high frequencies, γ and δ and the dominant low frequency, χ. Dashed lines are guides to the eye. e, f Proposed Fermi surfaces of FeSe1−xSx for different values of x as a slice at kz = π/c and kz = 0 (for Γ point) and 3D representation, respectively. In e for x = 0 (bottom) we sketched additional scenarios discussed in literature for the orbits originating from the electron bands5,19,22
Outside the nematic phase for x ~ 0.19, the background magnetoresistance is almost quadratic in magnetic field and the dominant low-frequency oscillation has disappeared (Fig. 1f, k). We detect a series of frequencies larger than those in the nematic phase (Fig. 3b); the observation of oscillations up to x ~ 0.19 is testament to the continued crystal quality, even at high substitution values. Here, the amplitude of the oscillations does not decay quite so rapidly with temperature, showing that the effective masses are lighter outside the nematic state; the highest observed frequency (1 kT), assigned to an enlarged outer hole pocket, δ, now having a mass around 3.2(5)me. This is consistent with the observation that the degree of electronic correlations is reduced significantly in the tetragonal phase towards FeS.11 We assume that the observed frequencies outside the nematic phase correspond to the lightest bands (Fig. 2c), in particular the outer hole band (δ orbit), as the outer electron band (γ orbit) has a heavier mass in the nematic state and it would be harder to observe it once the impurity scattering increases.17 The additional lightest band (286 T with an effective mass of 1.87(2)me) can be associated with the inner hole, χ; whereas, the 478 T frequency can be assigned to the largest inner electron band, α2, in Figs. 1r and 2c.
The angular dependence of quantum oscillations in Fig. 2e, f confirms that the observed orbits correspond to two-dimensional cylindrical Fermi surfaces (see Supplementary Fig. S6). Unusually, outside the nematic phase for x ~ 0.19 the largest amplitude of the highest frequency is observed not at θ = 0, as is normally expected for a Shubnikov-de Haas signal, but at θ = 30° (Fig. 3f). Furthermore, this angle is not the Yamaji angle,28 expected around θY = 65° (see Supplementary Fig. S6) at which a constructive interference occurs when the minimum and maximum orbit of a quasi-two-dimensional cylinder coincide (the Yamaji angle caused by the interference of the maximum and minima orbits of a corrugated Fermi surface occurs when J0(ckFtanθY) = 0, where J0 is the Bessel function, kF is the in-plane Fermi momentum and c is the lattice parameter). This effect can be caused by an interference between two orbits, γ and δ, with very close frequencies (that cannot be separated by FFT due to a limited field window in the normal state) and slightly different warping that give rise to different angular dispersions (Supplementary Fig. S6). The angular dependence of the lowest frequency oscillation λ dominating the magnetoresistance signal is shown in Fig. 3g, h. The oscillatory signal disappears around θ = 30° suggesting that this pocket is quasi-two-dimensional, as a 3D pocket would be expected to give oscillations at all angles.
Fermi surface evolution
The evolution of the low temperature Fermi surfaces and quasiparticle masses with chemical pressure in FeSe1−xSx is summarized in Fig. 2c. With chemical pressure the maximum orbits areas (γ and δ) increase monotonically with increasing x, even beyond the nematic phase boundaries. For the outer hole band (δ orbit) the increase in areas reflects the transition from an in-plane anisotropic to isotropic Fermi surface, as the ellipse transforms into a circle, but also as the in-plane areas generally increase; here quantum oscillations frequencies follow the same trends identified by ARPES studies (solid line in Fig. 2c).9,11,20
Furthermore, quantum oscillations show a dominant low-frequency oscillation with light mass from x ≥ 0.12, (λ in Fig. 2d), which decreases with chemical pressure (increasing in x) and eventually disappears outside the nematic phase (Fig. 1g–k and Supplementary Fig. S3). Thus, once the boundaries of the nematic phase have been crossed with chemical pressure the Fermi surface has a topological transition called a Lifshitz transition,29 which has not been detected before in ARPES studies at 10 K.9,11 Magnetotransport studies in FeSe1−xSx found that the high mobility small carrier density vanishes outside the nematic phase30,31 and it was suggested that this small pocket may have a non-trivial Berry phase.32
Fermi surface studies of FeSe under applied pressure,7 detected a dominant low-frequency oscillation outside the nematic phase, which was assigned to the Fermi surface reconstruction in the presence of the new structural and magnetic phase.13,14 The low frequency observed under pressure on the border of the nematic phase (~10 kbar) has a light effective mass,7 similar to λ, observed here in FeSe1−xSx in Fig. 2c). Thus, one can envisage that the evolution of the Fermi surface in the nematic state (Fig. 2a, b) under chemical and applied pressure share similar trends, which are also found for FeSe0.89S0.11 under applied pressure.33
As found in other iron-based superconductors, the Fermi surfaces of FeSe1−xSx are severely reduced in size compared with those predicted by band structure calculations (varying from a factor of 5 for FeSe towards a factor 3 for x ~ 0.17 as shown in Supplementary Fig. S7). This shrinking is an important consequence of strong orbitally dependent inter- and intra-band electronic interactions, significantly large in iron chalcogenides,3,34 but also found in many iron-based superconductors.24,26 These effects are suppressed to some extent once the bandwidth increases with sulphur substitution towards FeS.11
The effective masses evolution across the nematic phase in Fig. 3d indicated that the nematic state is a correlated electronic state and no sign of mass divergence was detected for δ orbit close to the nematic end point. As the electronic correlations assigned to the orbits with predominant dxz/dyz character (outer hole band, δ, in Fig. 2d) follow similar trends as Tc (Fig. 2a), these bands play a dominant role in the pairing mechanism. Our findings are in good agreement with the specific heat studies that show a slight increase in the Sommerfeld coefficient (7–9 mJ/mol K) inside the nematic phase before it drops again outside it35,36 as well as the ARPES studies that found the suppression of the electronic correlations in the tetragonal phase between x = 0.18 towards FeS.11 Furthermore, the effective mass of the prominent low-frequency oscillation, λ, is reduced significantly close to the nematic phase boundaries before disappearing, suggesting additional curvature changes of this Fermi surface before it suffers the topological transition. While clear signatures of criticality cannot be assessed over this narrow compositional range outside the nematic phase, it is worth mentioning for comparison that the signature of quantum criticality observed in BaFe2(As1−xPx)2 showed enhancement of the effective mass for the electron bands between 1.8 and 3.5me over a large compositional range (x = 0.4–1) outside the magnetic and nematic phase.24,37 In the end compound FeS, quantum oscillations have revealed very light effective masses of 0.6–0.8 me for some small orbits (below 210 T).38 For this reason, further study of quantum oscillations in FeSe1−xSx with higher x is desirable to establish whether critical nematic fluctuations play any role besides the effects caused by the suppression of the electronic correlations with the increased bandwidth.11
Discussion
Lifshitz transitions, driven by doping, chemical and applied pressure, magnetic field or correlations, can have dramatic effects on the electronic and superconducting properties. They have been detected as a function of electron doping, when the hole bands disappear and Tc increase, both in the electron-doped BaFe2As2,39 single crystals of FeSe40 and for the monolayer of FeSe on SrTiO3.41 Band structure calculations for isoelectronic FeSe and FeS also predict the disappearance of one of inner hole bands as a function of sulphur substitution (but they overestimate the experimental sizes of the Fermi surface as shown in Supplementary Fig. S6). Furthermore, DFT + DMFT calculations of FeSe under applied pressure show two topological transitions as the outer hole pocket expands, while the two inner hole pockets shrink and disappear.42 The degree of electronic correlations affects these bands with dxy or dxz/yz orbital character differently.43
In isoelectronic systems, like FeSe1−xSx, the hole bands are expected to be highly sensitive to the position of the chalcogen atom above the Fe plane, as found in other systems.23,24 We propose that the observed disappearance of the smallest orbit in quantum oscillations is linked to a topological change in the Fermi surface caused by strong increase in the interlayer warping, as the conducting layers come closer together with chemical pressure (similar to the applied pressure). ARPES studies on a composition of x ~ 0.18 suggest that the hole band at the Γ point is getting smaller compared with FeSe and the top of the band is only about 5 meV above the Fermi level (see Supplementary Fig. S4).11 Thus, the β orbit can be a prime candidate for the observed disappearance of a significant frequency in quantum oscillations (λ). Its absence will lead to a three-dimensional hole Fermi surface without of the ability for electron-hole scattering in the plane containing the Γ point, as shown in Fig. 2e, f. Other scenarios can invoke the disappearance of the inner electron band, α1, or magnetic field-induced Lifshitz transitions, as the energies of the very small inner hole and electron bands, can be comparable to the Zeeman energy (Supplementary Fig. S4).44
The changes in the electronic structure in FeSe1−xSx, due to the Lifshitz transitions would influence superconductivity significantly (Fig. 2e, f). First, a small increase in Tc at low x can be assigned to the increase in the density of states as the inner hole band (χ) crosses the Fermi level near x = 0.12, in agreement with specific heat studies.35,36 Furthermore, the nematic phase is a strongly correlated electronic phase45 and the effective masses of the outer hole band, δ (with predominant dxz/dyz character) follow similar trends to Tc, suggesting that this hole band plays an important role in the pairing. With further increases in x, superconductivity is weakened and it will be affected by the disappearance of the aforementioned small pocket, as a pairing channel through the centre of the Brillouin zone is lost (Fig. 2f). As the superconducting phase diagrams of FeSe1−xSx and that of FeSe under pressure show a similar small superconducting dome (see Fig. 2a and the superconducting region, S1, in Fig. 2b), they will be strongly influenced by the details of their electronic structure, and our study has indicated some of the trends to be taken into account.
The presence of small Fermi surfaces of FeSe1−xSx, harbours a fragile balance of competing interactions, that promote the stabilization of either nematic, spin-density wave or superconducting phases.46,47,48 Spin fluctuations increase at low temperature in the nematic phase of FeSe1−xSx close to the maximum Tc.49 As the sizes of the outer electron and hole bands coincide outside the nematic phase, the nesting and spin fluctuations in FeSe1−xSx would be significantly enhanced. On the other hand, the presence of small inner electron and hole bands can provide another pairing channel with different characteristics, as the Fermi energy of these bands approaches the gap energy, potentially pushing the system into a partial BCS-BEC crossover regime, where FFLO phases could be stabilized.44 Thus, the existence of a topological Lifshitz transition that induces significant changes in the kz dependence of the electronic and orbital electronic states together with the changes in electronic correlations in FeSe1−xSx, will significantly affect the pairing channels and the gap symmetry inside and outside the nematic phase, as found experimentally in recent studies.36,50
In summary, we have explored the evolution of the low-temperature electronic structure and electronic correlations across a nematic phase in the absence of magnetism in a highly tunable system, FeSe1−xSx. We found a robust strongly correlated state inside the nematic phase and the weakening of electronic correlations outside it. We observe the disappearance of a small high mobility pocket at the nematic phase boundary, indicative of a Lifshitz transition, not previously observed by spectroscopic studies. Our study provides vital information about the low temperature Fermi surface of a family of nematic superconductors and it helps to clarify the role played by a topological Lifshitz transition and electronic correlations across this unique phase diagram as well as the importance of accounting for the three-dimensionality pairing channels in these systems.
Methods
Samples were grown by the KCl/AlCl3 chemical vapour transport method and their compositions were determined using EDX measurements. More than 50 crystals were screened for transport measurements and the best crystals were measured in high magnetic fields. Preliminary magnetoresistivity and Hall effect measurements to identify the samples with the largest oscillatory signal were performed in pulsed magnetic fields up to 60 T in a dilution fridge and 70 T down to 1.5 K at the LNCMI in Toulouse, France. Magnetotransport measurements reported here were performed in high magnetic fields up to 45 T at NHMFL in Tallahassee, USA and up to 33 T at HFML in Nijmegen, The Netherlands, at low temperatures down to 0.35 K using 3He cryogenic systems and using low-noise transformers. Transport studies were performed by measuring the in-plane resistance with an electrical current of less than 3 mA flowing in the (ab) plane of the sample. Low contact resistances were achieved by soldering the gold wires directly to the samples. The magnetic field was applied either perpendicular to the structural ab layers (B||c, θ = 0°) or the sample was rotated in magnetic field towards c axis (B||(ab), θ = 90°).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. In accordance with the EPSRC policy framework on research data, access to the raw data will be made available through ORA depository at the University of Oxford at https://doi.org/10.5287/bodleian:wxAGnOgv6.
References
Fernandes, R. M., Chubukov, A. V. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Schattner, Y., Lederer, S., Kivelson, S. A. & Berg, E. Ising nematic quantum critical point in a metal: a Monte Carlo Study. Phys. Rev. X 6, 031028 (2016).
Watson, M. D. et al. Emergence of the nematic electronic state in FeSe. Phys. Rev. B 91, 155106 (2015).
Watson, M. D. et al. Evidence for unidirectional nematic bond ordering in FeSe. Phys. Rev. B 94, 201107 (2016).
Sprau, P. O. et al. Discovery of orbital-selective cooper pairing in FeSe. Science 357, 75 (2016).
Wen, C. H. P. et al. Anomalous correlation effects and unique phase diagram of electron-doped FeSe revealed by photoemission spectroscopy. Nat. Commun. 7, 10840 (2016).
Terashima, T. et al. Fermi surface reconstruction in FeSe under high pressure. Phys. Rev. B 93, 094505 (2016).
Burrard-Lucas, M. et al. Enhancement of the superconducting transition temperature of FeSe by intercalation of a molecular spacer layer. Nat. Mater. 12, 15–19 (2013).
Watson, M. D. et al. Suppression of orbital ordering by chemical pressure in FeSe1−xSx. Phys. Rev. B 92, 121108 (2015).
Hosoi, S. et al. Nematic quantum critical point without magnetism in FeSe1−xSx superconductors. Proc. Natl Acad. Sci. USA 113, 8139 (2016).
Reiss, P. et al. Suppression of electronic correlations by chemical pressure from FeSe to FeS. Phys. Rev. B 96, 121103 (2017).
Terashima, T. et al. Pressure-induced antiferromagnetic transition and phase diagram in FeSe. J. Phys. Soc. Jpn. 84, 063701 (2015).
Knöner, S. et al. Resistivity and magnetoresistance of FeSe single crystals under helium-gas pressure. Phys. Rev. B 91, 174510 (2015).
Kothapalli, K. et al. Strong cooperative coupling of pressure-induced magnetic order and nematicity in FeSe. Nat. Commun. 7, 12728 (2016).
Sun, J. P. et al. Dome-shaped magnetic order competing with high-temperature superconductivity at high pressures in FeSe. Nat. Commun. 7, 12146 (2016).
Matsuura, K. et al. Maximizing T c by tuning nematicity and magnetism in FeSe1−xSx superconductors. Nat. Commun. 8, 1143 (2017).
Shoenberg, D. Magnetic Oscillations in Metals. (Cambridge University Press, Cambridge, England, 1984).
Terashima, T. et al. Anomalous Fermi surface in FeSe seen by Shubnikov-de Haas oscillation measurements. Phys. Rev. B 90, 144517 (2014).
Watson, M. D., Haghighirad, A. A., Rhodes, L. C., Hoesch, M. & Kim, T. K. Electronic anisotropies revealed by detwinned angle-resolved photo-emission spectroscopy measurements of FeSe. New J. Phys. 19, 103021 (2017).
Coldea, A. I. & Watson, M. D. The key ingredients of the electronic structure of FeSe. Annu. Rev. Cond. Matt. Phys. 9, 125 (2018).
Watson, M. D. et al. Dichotomy between the hole and electron behavior in multiband superconductor FeSe probed by ultrahigh magnetic fields. Phys. Rev. Lett. 115, 027006 (2015).
Zhang, Y. et al. Distinctive orbital anisotropy observed in the nematic state of a FeSe thin film. Phys. Rev. B 94, 115153 (2016).
Putzke, C. et al. de Haas-van Alphen Study of the Fermi Surfaces of Superconducting LiFeP and LiFeAs. Phys. Rev. Lett. 108, 047002 (2012).
Shishido, H. et al. Evolution of the Fermi surface of BaFe2(As1−xPx)2 on entering the superconducting dome. Phys. Rev. Lett. 104, 1 (2010).
Arnold, B. J. et al. Nesting of electron and hole Fermi surfaces in nonsuperconducting BaFe2P2. Phys. Rev. B 83, 220504 (2011).
Coldea, A. I. et al. Fermi surface of superconducting LaFePO determined from quantum oscillations. Phys. Rev. Lett. 101, 216402 (2008).
Audouard, A. et al. Quantum oscillations and upper critical magnetic field of the iron-based superconductor FeSe. Europhys. Lett. 109, 27003 (2015).
Yamaji, K. On the angle dependence of the magnetoresistance in quasi-two-dimensional organic superconductors. J. Phys. Soc. Jpn. 58, 1520 (1989).
Lifshitz, I. Anomalies of electron characteristics of a metal in the high pressure region. JETP 11, 1130 (1960).
Ovchenkov, Y. A. et al. Highly mobile carriers in orthorhombic phases of iron-based superconductors FeSe1xSx. Supercond. Sci. Technol. 30, 035017 (2017).
Sun, Y., Pyon, S. & Tamegai, T. Electron carriers with possible Dirac-cone-like dispersion in FeSe1−xSx (x = 0 and 0:14) single crystals triggered by structural transition. Phys. Rev. B 93, 104502 (2016).
Kasahara, S. et al. Nontrivial orbital Berry phase in FeSe1−xSx superconductors. (in preparation).
Reiss, P. et al. Quenched nematic criticality separating two superconducting domes in an iron-based superconductor under pressure. submitted (2018).
Fanfarillo, L. et al. Orbital-dependent Fermi surface shrinking as a fingerprint of nematicity in FeSe. Phys. Rev. B 94, 155138 (2016).
Wang, L. et al. Superconductivity-enhanced nematicity and s+d gap symmetry in Fe(Se1−xSx). Phys Status Solidi (b) 254, 1–6, 1600153 (2016).
Sato, Y. Abrupt change of the superconducting gap structure at the nematic critical point in FeSe1–xSx. Proc. Natl Acad. Sci. USA 115, 1127–1231 (2018).
Walmsley, P. et al. Quasiparticle mass enhancement close to the quantum critical point in BaFe2(As1−xPx)2. Phys. Rev. Lett. 110, 257002 (2013).
Terashima, T. et al. Upper critical field and quantum oscillations in tetragonal superconducting FeS. Phys. Rev. B 94, 100503 (2016).
Liu, C. et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nat. Phys. 6, 419–423 (2010).
Ye, Z. R. et al. Simultaneous emergence of superconductivity, inter-pocket scattering and nematic fluctuation in potassium-coated FeSe superconductor. Preprint at arXiv:1512.02526 (2015).
Shi, X. et al. Enhanced superconductivity accompanying a Lifshitz transition in electron-doped FeSe monolayer. Nat. Comm. 8, 14988 (2017).
Mandal, S., Cohen, R. E. & Haule, K. Strong pressure-dependent electron-phonon coupling in FeSe. Phys. Rev. B 89, 220502 (2014).
Skornyakov, S. L., Anisimov, V. I., Vollhardt, D. & Leonov, I. Correlation strength, Lifshitz transition, and the emergence of a two-dimensional to three-dimensional crossover in FeSe under pressure. Phys. Rev. B 97, 115165 (2018).
Ptok, A., Kapcia, K. J., Cichy, A., Oleś, A. M. & Piekarz, P. Magnetic Lifshitz transition and its consequences in multi-band iron-based superconductors. Sci. Rep. 7, 41979 (2017).
Watson, M. D. et al. Formation of Hubbard-like bands as a fingerprint of strong electron-electron interactions in FeSe. Phys. Rev. B 95, 081106 (2017).
Chubukov, A. V., Khodas, M. & Fernandes, R. M. Magnetism, superconductivity, and spontaneous orbital order in iron-based superconductors: Which comes first and why? Phys. Rev. X 6, 041045 (2016).
Mukherjee, S., Kreisel, A., Hirschfeld, P. J. & Andersen, B. M. Model of electronic structure and superconductivity in orbitally ordered FeSe. Phys. Rev. Lett. 115, 026402 (2015).
Yamakawa, Y., Onari, S. & Kontani, H. Nematicity and magnetism in FeSe and other families of Fe-based superconductors. Phys. Rev. X 6, 021032 (2016).
Wiecki, P. et al. Persistent correlation between superconductivity and antiferromagnetic fluctuations near a nematic quantum critical point in FeSe1−xSx. Phys. Rev. B 98, 020507 (2018).
Hanaguri, T. et al. Two distinct superconducting pairing states divided by the nematic end point in FeSe1−xSx. Sci. Adv. 4, eaar6419 (2018).
Lifshitz, I. & Kosevich, A. On the theory of the Shubnikov-De Haas effect. Sov. Phys. JETP 2, 636 (1956).
Acknowledgements
We thank J. C. A. Prentice for computational support, N. Davies and A. Narayanan for preliminary sample preparation and R. Valenti, A. Chubukov and A. Shekhter for useful discussions. This work was mainly supported by EPSRC (EP/L001772/1, EP/I004475/1, EP/I017836/1). A.A.H. acknowledges the financial support of the Oxford Quantum Materials Platform Grant (EP/M020517/1). A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-1157490 and the State of Florida. This research was supported in part by the National Science Foundation under Grant No. NSF PHY17-48958. Part of this work was supported by HFML-RU/FOM and LNCMI-CNRS, members of the European Magnetic Field Laboratory (EMFL) and by EPSRC (UK) via its membership to the EMFL (grant no. EP/N01085X/1). Part of this work was supported by Programme Investissements d’ Avenir under the programme ANR-11-IDEX-0002-02, reference ANR-10-LABX-0037-NEXT. The authors would like to acknowledge the use of the University of Oxford Advanced Research Computing (ARC) facility in carrying out part of this work. A.I.C. thanks the hospitality of KITP supported by the National Science Foundation under Grant No. NSF PHY- 1125915. A.I.C. acknowledges an EPSRC Career Acceleration Fellowship (EP/I004475/1).
Author information
Authors and Affiliations
Contributions
A.I.C., S.F.B. and P.R. performed experiments in Tallahassee with support from E.S.K. A.I.C., S.F.B. and A.M. performed experiments in Nijmegen, A.A.H., T.W., S.K. and M.B. grew single crystals. M.B., M.D.W., S.K., T.S. performed preliminary transport measurements for screening single crystals. W.K., S.K., T.K. and T.S. performed-related preliminary experiments. S.S. and M.B. performed EDX measurements. A.I.C. and S.B. performed the data analysis. A.I.C. wrote the paper with contributions and comments from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coldea, A.I., Blake, S.F., Kasahara, S. et al. Evolution of the low-temperature Fermi surface of superconducting FeSe1−xSx across a nematic phase transition. npj Quant Mater 4, 2 (2019). https://doi.org/10.1038/s41535-018-0141-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-018-0141-0
This article is cited by
-
Unconventional superconductivity near a nematic instability in a multi-orbital system
npj Quantum Materials (2024)
-
Unusual crossover from Bardeen-Cooper-Schrieffer to Bose-Einstein-condensate superconductivity in iron chalcogenides
Communications Physics (2023)
-
Spin fluctuations from Bogoliubov Fermi surfaces in the superconducting state of S-substituted FeSe
Communications Physics (2023)
-
Resurgence of superconductivity and the role of dxy hole band in FeSe1−xTex
Communications Physics (2023)
-
Transport evidence for decoupled nematic and magnetic criticality in iron chalcogenides
Communications Physics (2022)