Tight Lieb–Robinson Bound for approximation ratio in quantum annealing

Abstract

Quantum annealing (QA) holds promise for optimization problems in quantum computing, especially for combinatorial optimization. This analog framework attracts attention for its potential to address complex problems. Its gate-based homologous, QAOA with proven performance, has attracted a lot of attention to the NISQ era. Several numerical benchmarks try to compare these two metaheuristics, however, classical computational power highly limits the performance insights. In this work, we introduce a parametrized version of QA enabling a precise 1-local analysis of the algorithm. We develop a tight Lieb–Robinson bound for regular graphs, achieving the best-known numerical value to analyze QA locally. Studying MaxCut over cubic graph as a benchmark optimization problem, we show that a linear-schedule QA with a 1-local analysis achieves an approximation ratio over 0.7020, outperforming any known 1-local algorithms.

Introduction

Quantum annealing (QA), firstly introduced by refs. ^1,2, is one of the most promising quantum algorithms to solve optimization problems^3,4. It runs on the quantum analog computational framework. Known as adiabatic quantum computing (AQC), it was coined by Fahri et al.⁵ in 2000 and stands for the analog part of the gate-based model. Although the two frameworks are known to be equivalent (one can efficiently simulate the other)⁶, their studies rely on different theoretical tools. QA has gained a lot of attention in the last decade because it seems well-suited to solve combinatorial optimization problems. A gate-based algorithm that has been largely studied, namely QAOA⁷, is QA-inspired and has brought a lot of attention to the NISQ era^8,9,10. The goal of quantum annealing is to let a quantum system evolve along a trajectory according to the Schrödinger equation subject to a problem-dependent Hamiltonian.

A recent study from ref. ¹¹ suggests that QAOA, even in the NISQ era, may bring a quantum advantage over classical algorithms for approximation in optimization problems. Several numerical studies like¹² suggest that QA performs well compared to QAOA. However, numerical studies in QA are rarely convincing because the size of the instance is limited by the classical computational power required to solve the Schrodinger equation or by the largest available quantum annealer. The downside of the approach is that, due to the limited size of the input data for numerical experiments, it is not possible to deduce a reliable asymptotic scale. To tackle this comparison, some researchers tried to develop new mathematical tools to derive an analytical bound on the algorithmic performance of QA. As it has been widely used to benchmark metaheuristics, we choose to focus on the approximation ratio of MaxCut over cubic (3-regular) graphs¹³. With one layer, standard QAOA achieves a ratio of 0.6925⁷, i.e., for any input, the algorithm outputs a solution whose number of cut edges is at least 0.6925 times the number of edges cut by the optimal solution. A zoo of variants¹³ of this algorithm has been proposed since but as in the original QAOA, we use the same initial and final Hamiltonians. A recent study in ref. ¹⁴ gives lower bounds on the number of rounds needed for some variants of QAOA to achieve a given ratio. In ref. ¹⁵, the authors manage to formally prove that constant time QA achieves a ratio of 0.5933 and, based on empirical studies, conjectured that the actual ratio is 0.6963. This last result has been improved by Banks, Brown and Warburton in ref. ¹⁶ to 0.6003. In ref. ¹⁷, Hastings shows a simple classical local algorithm that outperforms QAOA with an approximation ratio of 0.6980 (Fig. 1). By local algorithm, we mean that the decision of the algorithm on each node only depends on a ball of nodes at a constant distance from that node. The difficulty in comparing QA to QAOA or other local algorithms is that QA is non-local by nature. However, we can still make a local analysis of it. In 1972, Lieb and Robinson¹⁸ showed the existence of an information speed limit inside a quantum system. This means that, for a short enough evolution time T, the correlation between two remote sites of the quantum system decreases exponentially fast with respect to their distance q, typically in ${{{\mathcal{O}}}}(\frac{{T}^{q}}{q!})$. This observation can be used to analyze QA as a local algorithm by taking into account this exponential decrease in correlation strength. We refer the reader to ref. ¹⁹ for a recent extensive review on the Lieb–Robinson bound.

Fig. 1: Some approximation ratios for MaxCut over cubic graphs.

Only blue/greenish colored values result from 1-local algorithms. The highest proved ratio for MaxCut over cubic graphs is presented in²⁴.

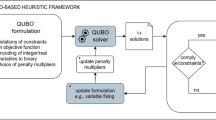
In this work, we develop a super tight Lieb–Robinson (LR) bound by using the commutativity graph construction from²⁰ over general regular graphs. This LR bound is adapted to linear-schedule QA applied to MaxCut as we will define in Section Results. In that setting, previously known state-of-the-art LR bounds^19,21 achieve interesting numerical values for q ≃ 100 when ours only needs q = 3 to reach similar values. We also slightly modify the standard initial Hamiltonian with a free parameter α in front of it. It appears that this additional degree of freedom in the algorithm (formulation) allows for a tighter performance analysis. Eventually, we end up proving that a 1-local analysis of QA brings the approximation ratio above 0.7020. This value shows that constant-time QA outperforms both single-layer QAOA and the best-known classical 1-local algorithm. Schedule optimization should bring further improvements, and we have suggested one with a cubic function. The global overview of the different steps used to derive an approximation ratio is detailed in Fig. 2.

Fig. 2

Overview of the analysis steps.

The first step consists of deriving a formula of the ratio that depends only on local balls B_p(X) centered on some edge X of a regular graph G. By local ball, we mean the subgraph of G generated by adding edges and nodes around X up to distance p from X (see Section Results for formal definition). In step 2, we turn a worst-case analysis over all possible graphs ${{{\mathcal{G}}}}$ into a worst-case analysis over a finite set of relatively small graphs ${{{{\mathcal{B}}}}}_{q}$ thanks to a Lieb–Robinson bound. Steps 3 and 4 deal with finding the minimum of interest by filtering the different balls after applying the global bound ε and the local one ε_loc on the leftovers. Eventually, these steps allow us to compute a numerical value for the approximation ratio depending on the running time T and the free parameter α.

In Section Results, we state our main result. We show how the different elements follow each other by formally defining the notion of approximation ratio, the parameterized version of QA(α), the notion of p − local analysis of QA, and presenting how a Lieb–Robinson bound can be used to compute the numerical value of the ratio. In Section Discussion, we discuss this result and the meaning of the parameter α, introduced for the tightness of the analysis. Although the construction is problem-dependent, we give some insight on the generalization of the construction for other degree, schedule and problems. We also hint a possible improvement with a non-linear schedule. In Section Method, we derive the method to prove the result. We demonstrate the derivation of the global and local LR bounds. In particular in Subsection Application to approximation ratio of MaxCut, we perform steps 3,4 and 5 of Fig. 2 to finish the proof of the theorem.

Results

The statement of our main result is the following:

Theorem (QA Approx.)

With a 1-local analysis, the approximation ratio reached by QA to solve MaxCut over cubic graphs is above 0.7020.

In this section, we define the approximation ratio which attests to the performance of QA and allows us to compare it with other algorithms. We then introduce the parametrized version of the QA process we will analyze and define a p − local analysis in the case of quantum annealing. Eventually, by introducing the Lieb–Robinson bound, we explain how QA can be locally analyzed in order to compare it to QAOA.

Approximation ratio

Given an input graph G on which we want to solve, an optimization problem C, and a probabilistic algorithm ${{{\mathcal{A}}}}$ that outputs a solution x for the problem C applied to G. One way to qualify the performance is to look at the average value reached by the output distribution of algorithm ${{{\mathcal{A}}}}$, written ${{\mathbb{E}}}_{{{{\mathcal{A}}}}}[C(G)]$. The metric used is the ratio of the latter quantity normalized by the optimal cost value C_opt(G) for the specific input. In practice, we are interested in the worst case scenario and define the approximation ratio as:

$${\rho }_{C,{{{\mathcal{A}}}}}=\mathop{\min }\limits_{G}\frac{{{\mathbb{E}}}_{{{{\mathcal{A}}}}}[C(G)]}{{C}_{opt}(G)}$$

(1)

For the rest of this work, we will focus on quantum annealing to solve a particular optimization problem called MaxCut over cubic graphs. The goal of MaxCut problem is to find a bi-partition that maximizes the number of edges across the bi-partition. Unless stated otherwise, we fix ${{{\mathcal{A}}}}=QA$ and we will remove its dependency on the variable notations for clarity. MaxCut is a well-known problem in fundamental computer science and has several applications in physics and electrical circuits²². It admits a natural encoding into a Hamiltonian that has the same interaction topology as the graph instance.

Parametrized QA

Given a graph G(V, E) in ${{{\mathcal{G}}}}$, a family of graph, on which we want to solve MaxCut, the target hamiltonian is ${H}_{1}^{G}=-{\sum }_{X\in E}{O}_{X}$ where ${O}_{X}=\frac{1-{\sigma }_{z}^{(a)}{\sigma }_{z}^{(b)}}{2}$ for the edge X = (a, b). With a minus, this Hamiltonian encodes − C, so the goal is to minimize this function. Starting from the uniform superposition $\left\vert {\psi }_{0}\right\rangle$ we are interested in the mean of ${H}_{1}^{G}$ of the final state $\left\vert {\psi }^{G}(T,\alpha )\right\rangle ={U}_{T,\alpha }^{G}\left\vert {\psi }_{0}\right\rangle$. Here, ${U}_{T,\alpha }^{G}$ denotes the unitary evolution operator under the time-dependent Hamiltonian $H(t,G)=(1-\frac{t}{T}){H}_{0}(\alpha )+\frac{t}{T}{H}_{1}^{G}$ and T the total annealing time. We chose a parameterized initial Hamiltonian ${H}_{0}(\alpha )=-{\sum }_{i}\frac{{\sigma }_{x}^{(i)}}{\alpha }$, where α > 0. This operator ${U}_{T,\alpha }^{G}$, corresponds to a Schrödinger evolution, i.e. is a solution of:

$$\forall t\in [0,T],\,i\hslash \frac{d{U}_{t,\alpha }^{G}}{dt}=H(t,G){U}_{t,\alpha }^{G}$$

The expected value at the end of the annealing process is ${\langle {H}_{1}^{G}\rangle }_{G,\alpha }=\left\langle {\psi }^{G}(T,\alpha )\right\vert {H}_{1}^{G}\left\vert {\psi }^{G}(T,\alpha )\right\rangle$ and thus, our metric of interest is

$${\rho }_{MC}=\mathop{\max }\limits_{T,\alpha }\mathop{\min }\limits_{G\in {{{\mathcal{G}}}}}\frac{-{\langle {H}_{1}^{G}\rangle }_{G,\alpha }}{{C}_{opt}(G)}.$$

Since we are interested in using local arguments to bound this quantity, we will restrict the family of graphs ${{{\mathcal{G}}}}$ to the set of 3-regular graphs. The goal is to find a good lower bound for this ratio. This can be achieved by separately upper bounding the denominator and lower bounding the numerator. By linearity, the numerator can be written as a sum over the edges ${\sum }_{X\in E}{\langle {O}_{X}\rangle }_{G,\alpha }$.

p − local analysis

Due to its analog nature, QA is non local, so to compare it to other optimization solver like QAOA or to local classical algorithms, we need to define a way to analyze it as a local algorithm. For any X ∈ E(G) and any positive integer p, we note B_p(X) the subgraph composed by nodes and edges situated on paths of length at most p from any endpoint of X. We note ${{{{\mathcal{B}}}}}_{p}$ the set of all possible balls B_p(X) over all graphs $G\in {{{\mathcal{G}}}}$ and all possible edges X. We call a p − local analysis of QA, an analysis that produces an approximation ratio that depends only on balls in ${{{{\mathcal{B}}}}}_{p}$. Let us develop the construction of a 0-local and 1-local analysis.

0-local

For any X ∈ E, a trivial lower bound of the summands in the numerator of the ratio is $\mathop{\min }\limits_{G\in {{{\mathcal{G}}}}}{\langle {O}_{X}\rangle }_{G}={\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}$, where ${{{\mathcal{G}}}}$ is the set of all 3-regular graphs. With the trivial bound on C_opt < ∣E∣, it gives the following lower bound on the approximation ratio:

$${\rho }_{MC}\ge \mathop{\max }\limits_{T,\alpha }{\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}.$$

Finding the latter value constitutes the approximation ratio of QA with 0-local analysis.

1-local

To improve this bound, we will consider the neighboring structure of each edge. For a p = 1-local analysis, we look at B₁(X), the ball of radius 1 around X. In 3-regular graphs, there are three such B₁(X), Ω₁ the square, Ω₂ the triangle and Ω₃ the double binary tree (see Fig. 3).

Fig. 3

All possible balls B₁(X) for X an edge (in green) in a 3-regular graph.

Coming back to our edge energies ${\langle {O}_{X}\rangle }_{G}$ for all X ∈ E: we can bound these terms by one of the following quantities ${\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{i}}=\min \{{\langle {O}_{X}\rangle }_{G}| G\in {{{\mathcal{G}}}},X\in E(G)\,{{\mbox{s.t.}}}\,{B}_{1}(X)={{{\Omega }}}_{i}\}$. Let us define n_i as the number of configurations Ω_i in G. Using the regularity constraints, we have that the number n₃ of edges in configuration Ω₃ is n₃ = ∣E∣ − 5n₁ − 3n₂ (see refs. ^7,15 for more details). The final expected energy can thus be lower bounded as:

$$-{\langle {H}_{1}^{G}\rangle }_{G}\ge {n}_{1}{\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{1}}+(4{n}_{1}+3{n}_{2}){\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{2}}+(| E| -5{n}_{1}-3{n}_{2}){\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{3}}$$

This expression still depends on the input graph through the variables n_i, and thus, still needs to be minimized over the positive integers n_i’s with the constraint that 4n₁ + 3n₂ ≤ ∣V∣. The upper bound on the optimal value C_opt can be refined by observing that at least one edge is uncut in the MaxCut solution in configuration Ω₁ and Ω₂, i.e. C_opt ≤ ∣E∣ − n₁ − n₂, where ∣E∣ = 3∣V∣/2. This gives the following lower bound for the approximation ratio:

$${\rho _{MC}} \ge \mathop {\max }\limits_{T,\alpha } \mathop {\mathop {\min }\limits_{n1,n2\,{\rm{st}}} }\limits_{4{n_1} + 3{n_2} \le \left| V \right|} \frac{{{n_1}\left\langle {{O_X}} \right\rangle _{\mathcal{G}}^{{\Omega _1}} + \left( {4{n_1} + 3{n_2}} \right)\left\langle {{O_X}} \right\rangle _{\mathcal{G}}^{{\Omega _2}} + \left( {\left| E \right| - 5{n_1} - 3{n_2}} \right)\left\langle {{O_X}} \right\rangle _{\mathcal{G}}^{{\Omega _3}}}}{{\left| E \right| - {n_1} - {n_2}}}$$

(2)

Given a quite loose condition on the value of ${\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{i}}$ which is satisfied in our case (see Supplementary Note 1 and Application to approximation ratio of MaxCut), the minimization gives n₁ = n₂ = 0 and the approximation ratio becomes ${\rho }_{MC}\ge \mathop{\max }\limits_{T,\alpha }{\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{3}}$. However, as in the 0-local analysis, the difficulty lies in computing the minimum over all graphs to find the values of ${\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{i}}$. Even for 3-regular graphs, because ${{{\mathcal{G}}}}$ is infinite, this minimum is intractable.

Lieb–Robinson bound

QA is a priori non-local, however Lieb and Robinson demonstrated that the information flow has a bounded speed inside a quantum system. In other words, limiting the amount of time during which the quantum system evolves also limits the distance at which two sites can strongly correlate. Using this on a QA process allows us to analyze QA locally. For a graph G(V, E), the idea is to approximate ${\langle {O}_{X}\rangle }_{G}$ by the energy of ${\langle {O}_{X}\rangle }_{{B}_{q}(X)}$. This step will ease the minimization task as now ${{{{\mathcal{B}}}}}_{q}$ is a finite family of graphs.

Local bound

Suppose that for any graph G, and any edge X of G, there exists a ε_loc(B_q(X), T, α) > 0 that upper bounds the absolute difference: $| {\langle {O}_{X}\rangle }_{G}-{\langle {O}_{X}\rangle }_{{B}_{q}(X)}| < {\varepsilon }_{loc}({B}_{q}(X),T,\alpha )$. The local aspect lies in the fact that ε_loc depends on the ball B_q(X). If such a bound exists, we have that ${\langle {O}_{X}\rangle }_{G}\ge {\langle {O}_{X}\rangle }_{{B}_{q}(X)}-{\varepsilon }_{loc}({B}_{q}(X),T,\alpha )$. This lower bound is satisfied for all graphs $G\in {{{\mathcal{G}}}}$. The only dependence on the input graph now lies in B_q(X). We can rewrite the minimization over ${{{\mathcal{G}}}}$ as:

$$\mathop{\min }\limits_{G\in {{{\mathcal{G}}}}}{\langle {O}_{X}\rangle }_{G}\ge \mathop{\min }\limits_{{B}_{q}(X)\in {{{{\mathcal{B}}}}}_{q}}\left({\langle {O}_{X}\rangle }_{{B}_{q}(X)}-{\varepsilon }_{loc}({B}_{q}(X),T,\alpha )\right)$$

(3)

$$\Rightarrow {\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}\ge {\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}^{* }$$

(4)

where ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}^{* }=\mathop{\min }\limits_{{B}_{q}(X)\in {{{{\mathcal{B}}}}}_{q}}({\langle {O}_{X}\rangle }_{{B}_{q}(X)}-{\varepsilon }_{loc}({B}_{q}(X),T,\alpha ))$. Therefore, the approximation ratio becomes, for QA as a 0-local algorithm,

$${\rho }_{MC}\ge \mathop{\max }\limits_{T,\alpha }{\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}^{* }$$

(5)

We can do the same for the 1-local analysis, when taking advantage of the neighborhood at radius 1 around the edge X. So we have that

$${\langle {O}_{X}\rangle }_{{{{\mathcal{G}}}}}^{{{{\Omega }}}_{i}}\ge \mathop{\min }\limits_{{B}_{q}}(X)\in {{{{\mathcal{B}}}}}_{q}\left({\langle {O}_{X}\rangle }_{{B}_{q}(X)}^{{{{\Omega }}}_{i}}-{\varepsilon }_{loc}({B}_{q}(X),T,\alpha )\right)={\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q,i}}^{* }$$

(6)

where ${{{{\mathcal{B}}}}}_{q,i}$ is the family of graphs ${B}_{q}(X)\in {{{{\mathcal{B}}}}}_{q}$ restricted to balls B_q(X) for which B₁(X) = Ω_i. The approximation ratio can be written as a new equation that depends only on these epsilons and worst edge energy among “small” ball of radius q:

$$\begin{array}{l}{\rho }_{MC}\ge \mathop{\max }\limits_{T,\alpha }\mathop{\min }\limits_{n1,n2\,{{\mbox{st}}}\,4{n}_{1}+3{n}_{2}\le | V| }\\\frac{{n}_{1}{\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q,1}}^{* }+(4{n}_{1}+3{n}_{2}){\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q,2}}^{* }+(| E| -5{n}_{1}-3{n}_{2}){\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q,3}}^{* }}{| E| -{n}_{1}-{n}_{2}}\end{array}$$

(7)

This method only helps the minimization task if q is small enough. Indeed, the size of ${{{{\mathcal{B}}}}}_{q}$ grows exponentially with q and and so does the size of ball. Computing ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}$ requires to solve the Schrodinger equation on balls of size up to ${{{\mathcal{O}}}}({2}^{q})$. For cubic graphs, q = 3 seems reasonable: all balls in ${{{{\mathcal{B}}}}}_{3}$ plus all the regular ones in ${{{{\mathcal{B}}}}}_{2}$ amounts for 930449 balls. However, we still need to have a large enough p so that the ε_loc(B_q(X), T, α) quantities are small enough to not degrade our lower bound (7) (typically, we want ε_loc(B_q(X), T, α) ≈ 10⁻²). Using state-of-the-art generic LR bounds^19,21 would require considering balls of radius q ≈ 100 in order to reach such a precision. Section Method is dedicated to the derivation of a tighter LR bound tailored exactly for the purpose of having reasonable ε_loc(B_q(X), T, α) values for q = 3.

Global bound

To avoid having to develop too many bounds ε_loc as the number of B_q(X) explodes exponentially, it can be useful to apply a global bound for most of the balls in the minimization task. We define it as

$$\varepsilon (q,T,\alpha )=\mathop{\max }\limits_{{B}_{q}(X)\in {{{{\mathcal{B}}}}}_{q}}{\varepsilon }_{loc}({B}_{q}(X),T,\alpha )$$

(8)

We will see in Section Method that this maximum is easy to derive from the analytical expression of the local bound. The global bound is used as follows:

$$\begin{array}{ll}\left({\langle {O}_{X}\rangle }_{{B}_{q}(X)}-{\varepsilon }_{loc}({B}_{q}(X),T,\alpha )\right)\,\ge {\langle {O}_{X}\rangle }_{{B}_{q}(X)}-\mathop{\max }\limits_{{B}_{p}(X)\in {{{{\mathcal{B}}}}}_{q}}{\varepsilon }_{loc}({B}_{q}(X),T,\alpha )\\ \quad\quad\qquad\qquad={\langle {O}_{X}\rangle }_{{B}_{q}(X)}-\varepsilon (q,T,\alpha )\\\quad\qquad\qquad\quad \Rightarrow {\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}^{* }\,\ge {\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}-\varepsilon (q,T,\alpha )\end{array}$$

Then for balls B_q(X) for which ${\langle {O}_{X}\rangle }_{{B}_{q}(X)}$ is large enough, the global bound is sufficient in the minimization task over ${{{{\mathcal{B}}}}}_{q}$.

In this sections we introduced different concepts and their role for obtaining the approximation ratio of QA solving MaxCut on cubic graphs, based on local analysis. This construction leads to the result state in Theorem QA Approx. In Section Method, we formally prove that the approximation ratio of QA for MaxCut on cubic graphs is greater than 0.7020 by finishing the steps 3,4 and 5 highlighted in Fig. 2. For that purpose we provide tighter LR bounds than the existing ones in the literature, leading to explicit numerical values for quantities ε, ε_loc and ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{q}}^{* }$.

Discussion

In this section, we discuss the role of α in the tightness of Theorem QA Approx, potential improvements and some directions for generalization.

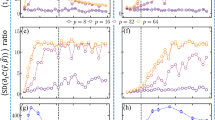
First, we discuss the effect of parameter α. In addition to the use of the commutativity graph, the exact value of the nested integrals alone would not have brought the ratio above the targeted numerical values of QAOA and Hastings local algorithm as we see in Fig. 8 (b) at α = 1. The introduction of the “hyperparameter” α significantly enhances the precision of the analysis. To attest this point, in Fig. 4, we plot the evolution of both the local ε_loc(g, T, α) and global ε(q, T, α) bounds against α for pairs (T, α) for which ${\langle {O}_{X}\rangle }_{g}=0.7092$ and g denotes the ball of Fig. 9. The value of 0.7092 is totally arbitrary and similar plots are achieved with different values. So we clearly see in Fig. 4 that the LR bound is minimal around α = 1.5 which means that the analysis of QA is tighter around this point.

Fig. 4: Tightness analysis.

Evolution of ε_loc(g, T, α) and ε(q = 3, T, α) against α for pairs (T, α) for which ${\langle {O}_{X}\rangle }_{g}=0.7092$ and g being the ball of Fig. 9.

We would like to draw readers’ attention to the fact that both the Hastings algorithm and QAOA also include one or two hyperparameters for obtaining their best ratio value. In this sense, our parameterized QA analysis is nothing more complex. However, although these two other algorithms produce a tight ratio value, QA’s is not tight simply because it is impossible to construct a graph such that every edge X has the g from Fig. 9 as its B₃(X).

On the LR bound itself, we can see from Fig. 8a that for many of the balls, the curves of the edge energy are indistinguishable. Indeed, at the pair (T, α) looked at, there is no visible difference in the value of the average edge energy. Even two balls in ${{{{\mathcal{B}}}}}_{2}$ can have the same trajectory. Informally, this suggests that LR bound is not yet tight, as the layer at distance 3 from the edge X does not impact the edge energy. As noted in ref. ¹⁵, neglecting the initial state greatly affects the accuracy of the bound. In order to strongly improve the analysis it would be crucial to be able to take into consideration the initial state; unfortunately, at this stage we lack of mathematical tools for this purpose. Another lead is indicated in ref. ¹⁹, in path counting. In fact, it seems that only direct paths contribute to LR bound. We explored this idea and the bound would reach 0.7041. However the result of ref. ¹⁹ cannot be adapted as is to our framework, so we cannot claim this approximation ratio at this stage.

How to improve the ratio?

An important field in the improvement of QA’s performance is the optimization of the schedule. Indeed, all the construction above works for a linear interpolation with no specific optimization but one can look at the Hamiltonian

$$H(t,G)=(1-f(t/T)){H}_{0}(\alpha )+f(t/T){H}_{1}^{G}$$

with f(t) such that f(0) = 0 and f(1) = 1. It is important to note that it also modifies the LR bound in the nested integrals. In commutativity graph notation, we have the h_v(t) = 1 − f(t/T) and h_e(t) = f(t/T). The challenge of this optimization is that one has to evaluate the energy on each of the 930449 balls for each tested schedule to formally prove an improvement of the ratio. However, a good insight can be reached by looking only at the 123 balls in ${{{{\mathcal{B}}}}}_{2}$. For instance, we tried few cubic functions to already see that with f(s) = 3.2s³ − 4.8s² + 2.6s, we should obtain a ratio above 0.7165 at T = 2.77 and α = 1.6.

Let us discuss some directions for generalizing the construction. We derived LR-type bounds applied to MaxCut on cubic graphs. We believe that our tools can be extended in several directions.

• 1. This work can be directly adapted to look for a other d − regular graphs. A formal derivation of this bound for any d − regular graphs requires to enumerate all the balls in ${{{{\mathcal{B}}}}}_{3}$ that can be completed in a d − regular graphs. The code can be easily edited for this purpose. However large balls are certainly too big to solve Schrodinger equation for d ≥ 4. It is still possible to get an intuition extrapolating the worst ball for d = 3 (Fig. 9). For example, the 1 − local approximation ratio for MaxCut over 4-regular graphs may be close to 0.67.

• 2. For p − local analysis of QA with p ≥ 2, the method developed here runs short as the time at which the best approximation ratio is achieved is certainly too large for the LR bound at q = 3. For a p = 2 − local analysis, our estimation gives that we would need to go up to q = 5 to achieve sufficiently small LR bound at time T ≃ 6.1, time for which the expected edge energy value seems to maximize. Nevertheless, by extrapolating at p = 2 the worst-case balls for p = 1 and by numerical experiments on these cases, we believe that the approximation ratio for MaxCut over cubic graphs is close to 0.77.

• 3. As discussed in the previous paragraph, the schedule can also be changed, the main work remains in the computation of the nested integrals of the schedule. Analytical bounds on these integrals are certainly too difficult to derive, but only numerical values are required to prove the bound. For any polynomial schedule, those integrals are easy to evaluate.

• 4. This construction can be applied to other combinatorial graph problems. For instance, in ref. ¹⁵, the authors applied a similar analysis to the Maximum Independent Set problem over cubic-graphs. More work is needed to adapt derive an ad hoc analytical formula for LR bound for this new problem Hamiltonian.

To conclude, in this work we developed a much tighter Lieb–Robinson bound compared to refs. ^19,21 by carefully manipulating the commutativity graph and the nested integral of the QA schedule. Despite the continuous aspect of QA, we defined the notion of p − local analysis of the metaheuristic by approximating the full algorithm using its restriction to bounded radius subgraphs. Our 1-local analysis of QA allows us to analytically compare its performances with the performances of single-layer QAOA for MaxCut over cubic graphs. The tightness of the LR bound we have derived enables us to reduce the exhaustive numerical simulation to a tractable task that can be completed in a few weeks. Finally, we introduced a parameter in the standard QA, enabling us to optimize the value of the ratio obtained and thus pass the 0.7 mark with a ratio going beyond 0.7020. This puts us ahead of single-layer QAOA and Hastings’ 1 − local algorithm for MaxCut over cubic graphs. The comparison has its limits, as the process we are studying is continuous and not intrinsically local, unlike the two algorithms mentioned. This work should be seen as a step forward in the study of quantum annealing, bringing more analytical tools to assess its algorithmic performances.

For future work, LR bound improvement can be tackled by considering the initial state information, which is not arbitrary. In ref. ¹⁵, the authors show that there is a considerable lost in tightness of the bound by neglecting the initial state. Also, as mentioned above, a slight improvement can be made to path counting. Then, our tight numerical result might be applied for a practical implementation of some Hamiltonian simulation schemes, e.g. ref. ²¹.

Methods

In this section we prove Theorem QA Approx in two steps. First we develop a tight enough LR bound using the commutativity graph structure introduced in ref. ²⁰ and by computing the exact values of the schedule’s nested integrals. This determines the required value of q to achieve the best provable ratio. The second step is purely numerical and requires to enumerate each ball B_q(X) and get the minimum of the final expected energy of the edge X inside these balls for each Ω_i, corrected by the LR bound. Our approach follows the algorithm presented in the last section of ref. ¹⁵.

Tight LR bound on regular graphs in QA

As mentioned in section Results, the minimization to obtain the approximation ratio is intractable when performed over the entire graph family. However, the LR bound helps to reduce the size of the set on which we have to minimize to a finite subfamily of graphs, namely ${{{{\mathcal{B}}}}}_{q}$ (see Eq. (4)).

First we seek to develop a local bound ε_loc(B_q(X), T, α) such that $| {\langle {O}_{X}\rangle }_{G}-{\langle {O}_{X}\rangle }_{{B}_{q}(X)}| < {\varepsilon }_{loc}({B}_{q}(X),T,\alpha )$ for all d-regular graphs G such that the ball at distance q around edge X corresponds to B_q(X). Let G be such a graph. It happens to be very difficult to manipulate this expression considering the initial state $\left\vert {\psi }_{0}\right\rangle$ so the first step (however costly in terms of tightness) is to get rid of this dependency by working directly with the evolution operator:

$$| {\langle {O}_{X}\rangle }_{G}-{\langle {O}_{X}\rangle }_{{B}_{q}(X)}| \le \left\Vert {O}_{X}^{G}(T)-{O}_{X}^{{B}_{q}(X)}(T)\right\Vert$$

where we introduce the evolved observable under ${U}_{T}^{G}$ and ${U}_{T}^{{B}_{q}(X)}$ respectively, once again dropping the α in the notation for clarity. They are defined as:

$${O}_{X}^{G}(T)={({U}_{T}^{G})}^{{\dagger} }{O}_{X}{U}_{T}^{G}$$

(9)

$${O}_{X}^{{B}_{q}(X)}(T)={({U}_{T}^{{B}_{q}(X)})}^{{\dagger} }{O}_{X}{U}_{T}^{{B}_{q}(X)}$$

(10)

In ref. ²³, the authors demonstrate that the evolution over a subset of nodes can also be expressed as :

$${O}_{X}^{{B}_{q}(X)}(T)=\int\,d\mu (U)U{O}_{X}^{G}(T){U}^{{\dagger} }$$

where μ(U) denotes the Haar measure over unitary operator U supported on S = V\V(B_p(X)). Noticing that $U{O}_{X}^{G}(T){U}^{{\dagger} }={O}_{X}^{G}(T)+U[{O}_{X}^{G}(T),{U}^{{\dagger} }]$, we can bound the quantity of interest $\Vert {O}_{X}^{G}(T)-{O}_{X}^{{B}_{q}(X)}(T)\Vert \le \int\,d\mu (U)\Vert [{O}_{X}^{G}(T),U]\Vert$ for any unitary U supported on S. We are then left to bound the norm of this commutator.

Let us introduce a helpful tool presented in ref. ²⁰: the commutativity graph G(V, E) associated to a Hamiltonian H(t, G) having local interactions. In general, we can write H(t) = ∑_jh_j(t)γ_j where γ_j are hermitian operators with norm less than unity and h_j(t) are time-dependent scalars. The commutativity graph of H(t) is constructed such that each operator γ_j is represented by a node j and two nodes j and k are connected if and only if [γ_j, γ_k] ≠ 0. The structure of the graph captures the commutative and non-commutative relationships between the operators in the Hamiltonian.

In the case of MaxCut, the total time-dependent Hamiltonian writes

$$H(t,G)=\mathop{\sum}\limits_{i\in V}(1-\frac{t}{T})\frac{{\sigma }_{x}^{(i)}}{\alpha }+\mathop{\sum}\limits_{(a,b)\in E}\frac{t}{T}\frac{1-{\sigma }_{z}^{(a)}{\sigma }_{z}^{(b)}}{2}$$

As described, the terms γ_j of the Hamiltonian are represented as nodes in the commutativity graph G. We can distinguish two types of nodes in V: those corresponding to interaction operators over the edges E of the original input graph, and those corresponding to local operators over nodes of V. This means that we have for e = (a, b) ∈ E, ${\gamma }_{e}=\frac{1-{\sigma }_{z}^{(a)}{\sigma }_{z}^{(b)}}{2}$ and for v ∈ V, ${\gamma }_{v}=\frac{{\sigma }_{x}^{(v)}}{\alpha }$. We can rewrite the total Hamiltonian as:

$$H(t,G)=\mathop{\sum}\limits_{v\in V}{h}_{v}(t){\gamma }_{v}+\mathop{\sum}\limits_{e\in E}{h}_{e}(t){\gamma }_{e}$$

Our notation fixes the time-dependent scalars at ${h}_{e}(t)=\frac{t}{T}$ for e ∈ E and ${h}_{v}(t)=1-\frac{t}{T}$ for v ∈ V. Also, it is obvious to see that the commutativity graph is bipartite. The only pairs that do not commute are pairs ${({\gamma }_{v},{\gamma }_{e})}_{v,e}$, where node v is incident to edge e in G. An example of commutativity graph is shown in Fig. 5.

Fig. 5: Example of a commutativity graph.

Example of a commutativity graph for the following Hamiltonian: $H(t,G)=\mathop{\sum }\nolimits_{i = 1}^{3}(1-\frac{t}{T})\frac{{\sigma }_{x}^{(i)}}{\alpha }+\frac{t}{T}\frac{1-{\sigma }_{z}^{(i)}{\sigma }_{z}^{(i+1)}}{2}$ where index i is taken modulo 3. Blue nodes represent 1-local operators and red nodes represent 2-interaction terms. In particular, blue nodes of G correspond to nodes of the original graph G, and red nodes correspond to its edges.

For a unitary A supported on S, we want to upper bound the quantity $\left\Vert [{O}_{X}^{G}(T),A]\right\Vert$. This edge X can be identified to a specific interaction term in the commutativity graph. Let us define X to be the node in G corresponding to the edge X and consider the operator ${\gamma }_{X}^{A}(T)=[{\gamma }_{X}(T),A]$ with ${\gamma }_{X}(t)={({U}_{T}^{G})}^{{\dagger} }{\gamma }_{X}{U}_{T}^{G}$, dropping the dependency on G. Still following the first steps in ref. ²⁰, we can arrive at a similar expression in the time-dependent regime (see Supplementary Note 2 for details):

$$\begin{array}{rc}\parallel {\gamma }_{X}^{A}(T)\parallel -\parallel {\gamma }_{X}^{A}(0)\parallel &\le \mathop{\sum}\limits_{v:\langle Xv\rangle \in {{{\bf{G}}}}}\int\nolimits_{0}^{T}{h}_{v}(t)\left\Vert \left[{\gamma }_{X}(t),{\gamma }_{v}^{A}(t)\right]\right\Vert dt\\ &\le \mathop{\sum}\limits_{v:\langle Xv\rangle \in {{{\bf{G}}}}}\int\nolimits_{0}^{T}(1-\frac{t}{T})\left\Vert {\gamma }_{v}^{A}(t)\right\Vert dt\end{array}$$

(11)

Now, we see on the right hand side of Eq. (11) that we have the norm of γ_v(t) for some node v adjacent to X in G. We can derive two update rules which we will use alternately depending on the considered node of G, i.e. depending whether it corresponds to an edge e of G or to a node v of G. These two rules are as follows:

$$\parallel {\gamma }_{e}^{A}(t)\parallel -\parallel {\gamma }_{e}^{A}(0)\parallel \le \mathop{\sum}\limits_{v:\langle ev\rangle \in {{{\bf{G}}}}}\int\nolimits_{0}^{t}(1-\frac{{t}^{{\prime} }}{T})\left\Vert {\gamma }_{v}^{A}({t}^{{\prime} })\right\Vert d{t}^{{\prime} }$$

(12)

$$\parallel {\gamma }_{v}^{A}(t)\parallel -\parallel {\gamma }_{v}^{A}(0)\parallel \le \frac{2}{\alpha }\mathop{\sum}\limits_{e:\langle ve\rangle \in {{{\bf{G}}}}}\int\nolimits_{0}^{t}\frac{{t}^{{\prime} }}{T}\left\Vert {\gamma }_{e}^{A}({t}^{{\prime} })\right\Vert d{t}^{{\prime} }$$

(13)

where we used two inequalities that for any t and any U:

$$\begin{array}{l}\parallel {\gamma }_{e}^{U}(t)\parallel \,=\,\parallel [{\gamma }_{e}(t),U]\parallel \le \frac{1}{2}2\parallel {\sigma }_{z}^{(i)}{\sigma }_{z}^{(j)}\parallel \parallel U\parallel \le \parallel U\parallel \\ \parallel {\gamma }_{v}^{U}(t)\parallel \,\,=\,\parallel [{\gamma }_{v}(t),U]\parallel \le \frac{1}{\alpha }2\parallel {\sigma }_{x}\parallel \parallel U\parallel \le \frac{2}{\alpha }\parallel U\parallel \end{array}$$

where (i, j) is the edge on which γ_e is applied and we used the trivial commutation of the identity with any matrix. Note that $\parallel {\gamma }_{j}^{A}(0)\parallel =0$ as long as j is inside B_q=k−1(X), so we can iterate up to 2k steps as the first node outside B_q(X) is a red node corresponding to an interaction term (see Fig. 6):

$$\begin{array}{l}\parallel {\gamma }_{X}^{A}(t)\parallel \le {\left(\frac{2}{\alpha }\right)}^{k}\mathop{\sum}\limits_{{v}_{1}:\langle X{v}_{1}\rangle \in {{{\bf{E}}}}}\mathop{\sum}\limits_{{e}_{1}:\langle {v}_{1}{e}_{1}\rangle \in {{{\bf{E}}}}}\ldots \mathop{\sum}\limits_{{e}_{k}:\langle {v}_{k}{e}_{k}\rangle \in {{{\bf{E}}}}}\int\nolimits_{0}^{t}{h}_{{v}_{1}}({t}_{1})\\\int\nolimits_{0}^{{t}_{1}}{h}_{{e}_{1}}({t}_{2})\ldots \int\nolimits_{0}^{{t}_{2k-1}}{h}_{{e}_{k}}({t}_{2k})\parallel {\gamma }_{{e}_{k}}^{A}({t}_{2k})\parallel d{t}_{2k}\ldots d{t}_{2}d{t}_{1}\end{array}$$

(14)

Now, let us introduce the following nested integral I_2k and I_2k+1 that appears in Eq. (14) where we replace each h_j(t_i) by its expression and we pull out the integral the factor T^2k and T^2k+1 respectively so that the integrals depend only on k:

$$\begin{array}{l}{I}_{2k}\,=\,\int\nolimits_{0}^{1}1-{u}_{1}\int\nolimits_{0}^{{u}_{1}}{u}_{2}\ldots \int\nolimits_{0}^{{u}_{2k-1}}{u}_{2k}d{u}_{2k}\ldots d{u}_{2}d{u}_{1}\\ {I}_{2k+1}\,=\,\int\nolimits_{0}^{1}1-{u}_{1}\int\nolimits_{0}^{{u}_{1}}{u}_{2}\ldots \int\nolimits_{0}^{{u}_{2k}}1-{u}_{2k+1}d{u}_{2k+1}\ldots d{u}_{2}d{u}_{1}\end{array}$$

There is no known closed form for these integrals but we can easily have the exact numerical values for at least the first 100 points and we can upper bound it as we show in Supplementary Note 3. We can then write, following Eq. (14):

$$\parallel {\gamma }_{X}^{A}(T)\parallel \le {T}^{2k}{\left(\frac{2}{\alpha }\right)}^{k}{I}_{2k}\mathop{\sum}\limits_{{v}_{1}:\langle X{v}_{1}\rangle \in {{{\bf{E}}}}}\mathop{\sum}\limits_{{e}_{1}:\langle {v}_{1}{e}_{1}\rangle \in {{{\bf{E}}}}}\ldots \mathop{\sum}\limits_{{e}_{k}:\langle {v}_{k}{e}_{k}\rangle \in {{{\bf{E}}}}}\mathop{\max }\limits_{t}\parallel {\gamma }_{{e}_{k}}^{A}(t)\parallel$$

where ${\gamma }_{{e}_{k}}^{A}(t)$ corresponds to an interaction node of the commutativity graph (i.e. red node) because we are at an even step. We used the fact that A is unitary and the dependence on B_q(X) lies in computing the size of the nested sum. This bound can be improved by applying the update rule of Eq. (11) and noticing that the first terms such that $\parallel {\gamma }_{{e}_{k}}^{A}(0)\parallel \ne 0$ only include all paths starting at X and ending in the first red node outside B_q=k−1(X) (the green area in Fig. 6) in 2k steps in G. After iterating several times, we get:

$$\begin{array}{rcl}\parallel {\gamma }_{X}^{A}(T)\parallel &\le&\,{T}^{2k}{\left(\frac{2}{\alpha }\right)}^{k}{I}_{2k}\times\#\{\,{{\mbox{path of length}}}\,2k:X{v}_{1}{e}_{1}\ldots{v}_{k}{e}_{k}\}\parallel {\gamma }_{{e}_{k}}^{A}(0)\parallel \\&+&\,{T}^{2k+1}{\left(\frac{2}{\alpha }\right)}^{k}{I}_{2k+1}\times \#\{\,{{\mbox{path of length}}}\,2k+1:X{v}_{1}{e}_{1}\ldots {v}_{k}{e}_{k}{v}_{k+1}\}\\&&\parallel {\gamma }_{{v}_{k+1}}^{A}(0)\parallel \\ &+&\,{T}^{2k+2}{\left(\frac{2}{\alpha }\right)}^{k+1}{I}_{2k+2}\times \#\{\,{{\mbox{path of length}}}\,2k+2:X{v}_{1}{e}_{1}\ldots {v}_{k+1}{e}_{k+1}\}\\&&\parallel {\gamma }_{{e}_{k+1}}^{A}(0)\parallel \\ &+&\,{T}^{2k+3}{\left(\frac{2}{\alpha }\right)}^{k+1}{I}_{2k+3}\times \#\{\,{{\mbox{path of length}}}\,2k+3:X{v}_{1}{e}_{1}\ldots {v}_{k+1}{e}_{k+1}{v}_{k+2}\}\\&&\parallel {\gamma }_{{v}_{k+2}}^{A}(0)\parallel \\ &+&\,{T}^{2k+4}{\left(\frac{2}{\alpha }\right)}^{k+2}{I}_{2k+4}\times \#\{\,{{\mbox{path of length}}}\,2k+4:X{v}_{1}{e}_{1}\ldots {v}_{k+2}{e}_{k+2}\}\\&&\parallel {\gamma }_{{e}_{k+2}}^{A}(0)\parallel \\ &+&\,{T}^{2k+5}{\left(\frac{2}{\alpha }\right)}^{k+2}{I}_{2k+5}\times \#\{\,{{\mbox{path of length}}}\,2k+5:X{v}_{1}{e}_{1}\ldots {v}_{k+2}{e}_{k+2}{v}_{k+3}\}\\&&\parallel {\gamma }_{{v}_{k+3}}^{A}(0)\parallel \\ &+&\,{T}^{2k+6}{\left(\frac{2}{\alpha }\right)}^{k+3}{I}_{2k+6}\mathop{\sum}\limits_{{v}_{1}:\langle X{v}_{1}\rangle \in {{{\bf{G}}}}}\mathop{\sum}\limits_{{e}_{1}:\langle {v}_{1}{e}_{1}\rangle \in {{{\bf{G}}}}}\ldots \mathop{\sum}\limits_{{e}_{k+2}:\langle {v}_{k+1}{e}_{k+2}\rangle \in {{{\bf{G}}}}}\mathop{\max }\limits_{t}\\&&\,\parallel {\gamma }_{{e}_{k+3}}^{A}(t)\parallel \\ &=&\,{\varepsilon }_{loc}({B}_{q = k-1}(X),T,\alpha )\end{array}$$

(15)

Fig. 6: Commutativity graph maximizing the LR bound.

Commutativity graph of the cubic graph that maximizes the LR bound. The shaded area shows an example for q = 2 = k − 1.

We stop at the seventh iteration because numerically it appears that the bound reaches a minimum before increasing again. Each path considered above ends outside B_q(X), because for the others we have $\parallel {\gamma }_{j}^{A}(0)\parallel \ne 0$ for j ∈ [e_k, v_k+1, e_k+1, v_k+2, e_k+2, v_k+3]. We also implicitly extend B_q(X) so as to maximize the number of paths in Eq. (15). Thanks to the upper bound of the integrals detailed in Supplementary Note 3, it is easy to see that the derived bound is decreasing with k and thus with q meaning that we have the following corollary:

Corollary

For any q > 0 and any edge X inside a d − regular graph,

$$\forall j \,>\, 0,{\varepsilon }_{loc}({B}_{q+j}(X),T,\alpha )\le {\varepsilon }_{loc}({B}_{q}(X),T,\alpha )$$

the same goes for the global bound as taking the max preserves the inequality:

$$\forall j \,>\, 0,\varepsilon (q+j,T,\alpha )\le \varepsilon (q,T,\alpha )$$

For the local bound, we need to compute for each ball B_q(X) the number of paths. In practice, a subroutine counting the number of paths of a given size is used to compute the local bound. The last term with the multiple sums is counting for (2d)^k+3 as at each interaction term there are d possible choices of nodes and only 2 at the others. In this subsection we detailed the derivation of the LR local bound Eq. (15). In the next subsection, we pursue the derivation to get the global bound by taking the maximal number of paths.

Global LR bound

In this subsection, we use Eq. (15) to derive the global LR bound. As defined in Section Results, the global bound is obtained by considering the maximum of the local bound Eq. (15) over all balls in ${{{{\mathcal{B}}}}}_{q}$. To this end, we consider the worst-case scenario, i.e. the ball maximizing the possible number of paths. It is trivial to see that this corresponds to the cycle-free ball (Fig. 6).

In this cycle-free ball, we can count the number of paths corresponding to each term in LR bound’s equation. In Fig. 7, we depict example paths for each of the necessary cases that we detail below.

Fig. 7: Paths counting.

Example of different paths starting at X on the commutativity graph for the global bound with k = 3. a A simple path (Xv₁e₁v₂e₂v₃e₃) in pink of length 2k, b a green path (Xv₁e₁v₂e_bv₂e₂v₃e₃) of length 2k + 2 with a back-and-forth on one edge, c in orange a path (Xv₁e_rv_re_rv₁e₁v₂e₂v₃e₃) of length 2k + 4 with a back-and-forth on a branch of two edges and d in blue a path (Xv₁e_rv₁e₁v₂e₂v₃e₂v₃e₃) of length 2k + 4 with two back-and-forth on two edges at distance at most one from the simple path.

For the first two terms, only direct simple paths reach the outside of B_q(X), and there are 2(d−1)^k of them. The factor 2 comes from the initial choice at node X, you can go either left or right in Fig. 6. Once the side has been chosen, at each blue node (node v_r), there are d − 1 possibilities, as the path can not go backwards by definition of direct single paths. In a path from X to the first node outside B_q=k−1(X), i.e. of length 2k, there are k blue nodes, bringing the total number of direct simple paths to 2(d−1)^k (path Fig. 7a). The same number of paths is found for direct paths of length 2k + 1.

Then, for the third and fourth terms, we can distinguish simple direct paths that go one step further in G, i.e. of length 2k + 2 and 2k + 3 respectively, from non-direct paths, i.e. passing several times through the same node or edge. For the third term counting paths of length 2k + 2, similarly to above, there are 2(d−1)^k+1 direct paths. For the non-direct ones, we need to count every edge that can be used at least twice in the path (path Fig. 7b. At first, there are the two edges that start from X, then (d − 1) at each blue node on the path and + 1 at each red node, making a total of 2 + ((d − 1) + 1)*k edges that can be used twice in the 2(d−1)^k possible paths. Therefore, the total number of paths in the third term is 2(d−1)^k+1 + (2 + dk)*2(d−1)^k. For the fourth term, we use similar reasoning to arrive at 2(d−1)^k+1 + (dk + 2 + d − 1)*2(d−1)^k paths.

Let us see how the last two terms are derived. For the fifth term, we need to count all paths of length 2k + 4 that lead to a red node outside the shaded area. There are three types of path: direct paths up to e_k+2 counting for 2(d−1)^k+2, those with exactly one edge taking two or three times, i.e. reaching e_k+1 counting for (d(k + 1) + 2)*2(d−1)^k+1 and those reaching e_k counting for $\left[(dk+2)+\left(\begin{array}{c}dk+2\\ 2\end{array}\right)+2(d-1)+k\right]* 2{(d-1)}^{k}$. In the latter, a distinction is made: either an edge is used 4 or 5 times, or 2 different edges at a distance at most one from the direct path can be used 2 or 3 times (path Fig. 7d), or finally choose a branch of length 2 far from the direct path (path Fig. 7c). Similar reasoning is used for the sixth term.

We can then substitute the path counting in Eq. (15) to derive the following closed-form:

$$\begin{array}{rcl}\parallel {\gamma }_{X}^{A}(t)\parallel &\le &\,{T}^{2k}{\left(\frac{2}{\alpha }\right)}^{k}{I}_{2k}\times 2{(d-1)}^{k}+{T}^{2k+1}{\left(\frac{2}{\alpha }\right)}^{k+1}{I}_{2k+1}\times 2{(d-1)}^{k}\\ &+&\,{T}^{2k+2}{\left(\frac{2}{\alpha }\right)}^{k+1}{I}_{2k+2}\times 2{(d-1)}^{k}\left[d(k+1)+1\right]\\&+&\,{T}^{2k+3}{\left(\frac{2}{\alpha }\right)}^{k+2}{I}_{2k+3}\times 2{(d-1)}^{k}\left[d(k+2)\right]\\ &+&\,{T}^{2k+4}{\left(\frac{2}{\alpha }\right)}^{k+2}{I}_{2k+4}\times 2{(d-1)}^{k}\left[{d}^{2}\frac{{(k+1)}^{2}+3}{2}+d\frac{3k+2}{2}+k\right]\\ &+&\,{T}^{2k+5}{\left(\frac{2}{\alpha }\right)}^{k+3}{I}_{2k+5}\times 2{(d-1)}^{k}\left[{d}^{2}\frac{{(k+2)}^{2}+3}{2}+d\frac{k+1}{2}+k-1\right]\\ &+&\,{T}^{2k+6}{\left(\frac{2}{\alpha }\right)}^{k+3}{I}_{2k+6}\times {(2d)}^{k+3}=\varepsilon (q=k-1,T,\alpha )\end{array}$$

(16)

In this subsection, we developed the proof of our LR bound for any d − regular graph on which we want to solve MaxCut with a quantum annealing process. This bound achieves the best numerical value compared to the state-of-the-art of LR bounds. This is due to the fact that we have finely evaluated the nested integral with the standard schedule and used the commutativity graph of the Hamiltonian to tighten the bound. Here the free parameter α plays an important role: optimizing over its value will allow us to control the tightness of the bound (16). This point is further discussed in Section Discussion. In the next subsection, we apply the derived bounds (global and local) to obtain a numerical value of the approximation ratio for a 1-local analysis of QA.

Application to approximation ratio of MaxCut

In this subsection, we use the previously derived LR bounds to determine the approximation ratio of MaxCut over cubic graph with QA analyzed as a 1 − local algorithm. The proof of the Theorem QA Approx proceeds with step 3, 4 and eventually 5, as illustrated in the overview of Fig. 2. We will use the Eq. (7) to derive the approximation ratio with the 1 − local analysis.

For this purpose, after rigorous errors and trials, we set specific values T = 3.33, α = 1.53 and q = 3, that establish the global bound ε(q, T, α). In order to compute the required minimums of Eq. (6), ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{3,i}}^{* }$, we need to enumerate all balls in ${{{{\mathcal{B}}}}}_{3}$ and all cubic graphs in ${{{{\mathcal{B}}}}}_{2}$. We follow a smart hash-based iterative algorithm detailed in Supplementary Note 4. The algorithm generated 930449 balls. Employing the AnalogQPU simulator of Eviden Qaptiva see Supplementary Note 4), we solve the Schrödinger equation to get the final state $\left\vert {\psi }^{{B}_{3}(X)}(T,\alpha )\right\rangle$ as described in the paragraph “Parametrized QA” of Section Results. This allows to explicitly evaluate the value of ${\langle {O}_{X}\rangle }_{{B}_{3}(X)}$ for each ball in ${{{{\mathcal{B}}}}}_{3}$. We subtract the value of the global LR bound to the expected edge energy for each ball. To narrow down our selection, we retain only those balls for which $| {\langle {O}_{X}\rangle }_{{B}_{3}(X)}-\varepsilon (q,T,\alpha )| < 0.7020$. This initial step corresponds to step 3 of Fig. 2 and leads to the values for ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{3,1}}^{* }=0.5502$ and ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{3,2}}^{* }=0.6265$. These values satisfy the condition (see Supplementary Note 1) where the ratio reduces to ${\rho }_{MC}\ge {\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{3,3}}^{* }$. In other words, the critical balls correspond to configurations Ω₃ (see Fig. 3), as it usually happens in QA and QAOA algorithms for MaxCut^7,15. Consequently, our goal is to maximize this minimum.

We are left with 7071 balls B₃(X) with configuration Ω₃ at distance 1 around X, to which we apply the local bound. To compute the local bound, we have access to a path-counting algorithm as there is no closed form like the global bound. To find the maximum over parameters T and α, in Fig. 8, we plot the evolution of (a) $\mathop{\max }\limits_{T}({\langle {O}_{X}\rangle }_{{B}_{3}(X)}-\varepsilon (3,T,\alpha ))$ and (b) $\mathop{\max }\limits_{T}({\langle {O}_{X}\rangle }_{{B}_{3}(X)}-{\varepsilon }_{loc}({B}_{3}(X),T,\alpha ))$ against α for the 18 worst balls B₃(X) according to the global and local bounds respectively.

Fig. 8: Edge energy of the worst balls against α.

Evolution of (a)$\mathop{\max }\limits_{T}\left({\langle {O}_{X}\rangle }_{{B}_{3}(X)}-\varepsilon (3,T,\alpha )\right)$ and (b)$\mathop{\max }\limits_{T}\left({\langle {O}_{X}\rangle }_{{B}_{3}(X)}-{\varepsilon }_{loc}({B}_{3}(X),T,\alpha )\right)$ against α for the 18 worst balls for which it goes under 0.7020 with the global bound.

The analysis reveals that around α = 1.5 all these balls surpass the threshold of 0.7020, with the worst ball depicted in Fig. 9. This plot finally fixes the value of ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{3,3}}^{* }=0.70208\ldots$ which proves Theorem QA Approx.

Fig. 9: Worst edge configuration.

Ball B₃(X) achieving the minimum ${\langle {O}_{X}\rangle }_{{{{{\mathcal{B}}}}}_{3,3}}^{* }=0.70208\ldots$.

To sum up, the constant-time analysis of Quantum Annealing (QA) for MaxCut over cubic graphs, analyzed as a 1-local algorithm, achieves an approximation ratio exceeding 0.7020. This result goes beyond any known ratio of 1-local algorithms, whether quantum or classical.